（追記有り）中学でも分かるガロアの証明➃『剰余群』について

2024年2月2日 12:06

　ここでは、剰余類どうしに新たに演算を定義して、その演算に関して剰余類の集合は群（これを剰余群という）になることを証明していきます。ガロアによる偉大な発見です。

　ますは、本シリーズ (28) ～ (30) でやった定義、重要事項を記していきます。

（復習）群の定義

　空でない集合 $${G}$$ の任意の要素 $${a, b, c}$$ の間に１つの演算 $${*}$$ が規定されているとする。
　この集合 $${G}$$ の任意の要素 $${a, b, c}$$ が、その演算 $${*}$$ に関して次の条件を満たすとき、$${G}$$ は演算 $${*}$$ に関して群であるという。
(1)　$${a*b}$$ は $${G}$$ の要素である。
(2)　交換法則 $${(a*b)*c=a*(b*c)}$$ が成り立つ。
(3)　$${a*e=e*a=a}$$ となる単位元 $${e}$$ が $${G}$$ に存在する。
(4)　$${a*x=x*a=e}$$ となる逆元 $${x}$$ が $${G}$$ に存在する。

＊＊＊

(1) を満たすことを、集合 $${\bm G}$$ は演算 $${\bm *}$$ について閉じているといいます。演算の結果、集合 $${G}$$ からはみ出さないことを意味します。
(2) は、カッコを気にしないで、どこから演算を施してもよいことを保証します。
(3) は、左右どちらから演算を施しても変化しない要素の存在です。その要素を単位元といいます。
(4) は、左右両方から演算を施すと単位元となる要素の存在です。その要素を逆元といいます。

　要するに群とは、イメージとして
(1)　全部そろっている
(2)　つなげることができる
(3)　変えないことができる
(4)　元に戻すことができる
の４つの条件が成り立つ要素の集まり（集合）です（本シリーズ (28)）。

　３次置換の集合は群であり、それを３次対称群 $${S_3}$$ と表します。
　$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
$${S_3}$$ の置換の積（合成）の対応表は、次のようになります（本シリーズ (28)）。

$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
& id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline
\rho_2 & \rho_2 & \rho_3 & id & \tau_3 & \tau_1 & \tau_2\\ \hline
\rho_3 & \rho_3 & id & \rho_2 & \tau_2 & \tau_3 & \tau_1\\ \hline
\tau_1 & \tau_1 & \tau_2 & \tau_3 & id & \rho_2 & \rho_3\\ \hline
\tau_2 & \tau_2 & \tau_3 & \tau_1 & \rho_3 & id & \rho_2\\ \hline
\tau_3 & \tau_3 & \tau_1 & \tau_2 & \rho_2 & \rho_3 & id
\end{array}
$$

（復習）部分群の定義

　ある群 $${G}$$ の空でない部分集合 $${H}$$ が同じ演算で群になるとき、その部分集合 $${H}$$ を、 $${G}$$ の『部分群』といいます。
　ここで重要なのは、あくまでも「同じ演算で」ということです。もとの群がたし算に関して群となる場合、その部分群もたし算に関して群となります（本シリーズ (29)）。

　なお、自分自身や、要素が単位元だけからなる集合は、すべての群の部分群となるため『自明な部分群』といいます。
　３次対称群 $${S_3}$$ の部分群には、全部で以下の６通りがありますが、$${S_3}$$ と $${\{id\}}$$ が自明な部分群となります。また、自明な部分群以外の部分群を『真部分群』といいます。
　$${\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$（自明な部分群）
　$${\{id, \rho_2, \rho_3\}}$$（真部分群）
　$${\{id, \tau_1\}}$$（真部分群）
　$${\{id, \tau_2\}}$$（真部分群）
　$${\{id, \tau_3\}}$$（真部分群）
　$${\{id\}}$$（自明な部分群）

　部分群について、次の正規部分群は重要です。

（復習）正規部分群の定義

　$${N}$$ を群 $${G}$$ の部分群とする。$${G}$$ のすべての要素 $${g}$$ について

$$
\begin{align*}
gN=Ng
\end{align*}
$$

を満たすとき、$${N}$$ を $${G}$$ の正規部分群という。

＊＊＊

　$${gN=Ng}$$ とは、あくまでも集合として等しいことを意味します。つまり、$${G}$$ のすべての要素 $${g}$$ について、左剰余類 $${gN}$$（という集合）の要素と、右剰余類 $${Ng}$$（という集合）の要素が、同じになるということです（本シリーズ (30)）。

$$
\begin{gather*}
\underset{左剰余類}{gN}\hspace{-5pt}=\hspace{-5pt}\underset{右剰余類}{Ng}\\[-3pt]
\hspace{1pt}\uparrow\\[-5pt]
\hspace{1pt}{\footnotesize 集合の要素が同じ}\\[-5pt]
\hspace{0pt}{\footnotesize（集合として等しい）}
\end{gather*}
$$

　$${S_3}$$ の部分群のうち、正規部分群となるのは、自分自身 $${S_3}$$、単位元のみからなる集合 $${\{id\}}$$、及び遇置換のみからなる３次交代群
　$${A_3=\{id, \rho_2, \rho_3\}}$$
の３つのみです。そのうち、自明な部分群である $${S_3}$$ と $${\{id\}}$$ を『自明な正規部分群』といいます。
　$${\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$ （自明な）正規部分群である
　$${\{id, \rho_2, \rho_3\}}$$　正規部分群である
　$${\{id, \tau_1\}}$$　正規部分群ではない
　$${\{id, \tau_2\}}$$　正規部分群ではない
　$${\{id, \tau_3\}}$$　正規部分群ではない
　$${\{id\}}$$ （自明な）正規部分群である

　正規部分群によって、ある法則をもって群をいくつかのグループに分けることができます。それが剰余類による類別です。正規部分群による剰余類を考えた場合、その剰余類による類別の方法は、左剰余類と右剰余類で同じ類別となる、というのがガロアの発見した重要な定理です。

（復習）正規部分群による類別

　一般に、正規部分群によって類別する場合は、左剰余類で類別する場合と、右剰余類で類別する場合とでは、必ず同じ類別になります（本シリーズ (30)）。

（図説）

　$${S_3}$$ の正規部分群 $${N=\{id, \rho_2, \rho_3\}}$$ について

＜左剰余類による類別＞

$${\hspace{80pt}\Updownarrow}$$ 類別の方法は同じ

＜右剰余類による類別＞

　一方、正規部分群ではない部分群によって類別する場合は、左剰余類で類別する場合と、右剰余類で類別する場合とでは、必ず異なる類別になります。

（図説）

　$${S_3}$$ の正規部分群ではない部分群 $${M=\{id, \tau_1\}}$$ について

＜左剰余類による類別＞

$${\hspace{98pt}\Updownarrow}$$ 類別の方法は異なる

＜右剰余類による類別＞

　$${\rho_2M\ne M\rho_2}$$、$${\rho_3M\ne M\rho_3}$$ であることから、$${M=\{id, \tau_1\}}$$ は正規部分群ではありません。それにより、上図の様に左剰余類による類別と、右剰余類による類別は異なることが見てとれます。

　復習はここで終わり、次からいよいよ剰余類どうしに新たに演算を定義していきます。

剰余類どうしに演算を定義

　ここで、正規部分群についての左剰余類どうし、および右剰余類どうしについて、次のように新たに演算を定義します。まずは左剰余類について考えます。本記事最後の方で、右剰余類についても言及します。

左剰余類どうしの演算の定義

　$${N}$$ を群 $${G}$$ の正規部分群とする。$${a, b}$$ を $${G}$$ の任意の要素とするとき、左剰余類 $${aN , bN}$$ による演算 $${\circ}$$ を次のように定義する。

$$
\begin{align*}
aN \circ bN\hspace{-2pt}\underset{def}{=}\hspace{-1pt}abN
\end{align*}
$$

これを簡単に、『左剰余類の積』という場合があります。
　なお「$${def}$$」とは定義 (definition) の意味です。

＊＊＊

　この式について簡単に説明すると
　$${a}$$ を代表元とする左剰余類 $${aN}$$
　$${b}$$ を代表元とする左剰余類 $${bN}$$
があったとき、$${aN}$$ と $${bN}$$ の演算
　$${aN \circ bN}$$
の結果を、「置換の積 $${ab}$$ を代表元とする左剰余類 $${abN}$$ と定義する」ということです（代表元については本シリーズ (30)）。

$$
\begin{align*}
&aN \circ bN\hspace{-2pt}\underset{def}{=}\hspace{-1pt}abN\\[-10pt]
&\hspace{-5pt}{\footnotesize \uparrow \atop {a を \atop 代表元}}{\footnotesize \uparrow \atop {b を \atop 代表元}}\hspace{9pt}
{\footnotesize \uparrow \atop {ab を \atop 代表元}}
\end{align*}
$$

　やや抽象的なので、具体的に解説します。

　３次対称群
　$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
と、その正規部分群
　$${N=\{id, \rho_2, \rho_3\}}$$
について、演算 $${\circ}$$ の定義より

$$
\begin{align*}
idN\circ\tau_1N\hspace{-2pt}\underset{def}{=}\hspace{-1pt}id\tau_1N\\
\rho_2N\circ\tau_3N\hspace{-2pt}\underset{def}{=}\hspace{-1pt}\rho_2\tau_3N
\end{align*}
$$

となります。つまり
　$${idN\circ\tau_1N}$$
は、置換の積 $${id\tau_1}$$ を代表元とする左剰余類 $${id\tau_1N}$$ と定義し、
　$${\rho_2N\circ\tau_3N}$$
は、置換の積 $${\rho_2\tau_3}$$ を代表元とする左剰余類 $${\rho_2\tau_3N}$$ と定義します。

$$
\begin{align*}
&idN\circ\tau_1N\hspace{-2pt}\underset{def}{=}\hspace{-1pt}id\tau_1N\\[-8pt]
&\hspace{-2pt}{\footnotesize \uparrow \atop {id を \atop 代表元}}\hspace{4pt}{\footnotesize \uparrow \atop {\tau_1 を \atop 代表元}}\hspace{12pt}
{\footnotesize \uparrow \atop {id\tau_1 を \atop 代表元}}\\[10pt]
&\rho_2N\circ\tau_3N\hspace{-2pt}\underset{def}{=}\hspace{-1pt}\rho_2\tau_3N\\[-8pt]
&\hspace{-2pt}{\footnotesize \uparrow \atop {\rho_2 を \atop 代表元}}\hspace{4pt}{\footnotesize \uparrow \atop {\tau_3 を \atop 代表元}}\hspace{12pt}
{\footnotesize \uparrow \atop {\rho_2\tau_3 を \atop 代表元}}
\end{align*}
$$

　すると、３次対称群 $${S_3}$$ の置換の積の演算表

$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
& id & \rho_2 & \rho_3 & \underline{\tau_1} & \tau_2 & \utilde{\tau_3}\\ \hline\hline
\underline{id} & id & \rho_2 & \rho_3 & \underline{\tau_1} & \tau_2 & \tau_3\\ \hline
\utilde{\rho_2} & \rho_2 & \rho_3 & id & \tau_3 & \tau_1 & \utilde{\tau_2}\\ \hline
\rho_3 & \rho_3 & id & \rho_2 & \tau_2 & \tau_3 & \tau_1\\ \hline
\tau_1 & \tau_1 & \tau_2 & \tau_3 & id & \rho_2 & \rho_3\\ \hline
\tau_2 & \tau_2 & \tau_3 & \tau_1 & \rho_3 & id & \rho_2\\ \hline
\tau_3 & \tau_3 & \tau_1 & \tau_2 & \rho_2 & \rho_3 & id
\end{array}
$$

より、置換の積は
　$${id\tau_1=\tau_1　\cdots (*1)}$$（下線部）
　$${\rho_2\tau_3=\tau_2　\cdots (*2)}$$（波線部）
と定まるので、左剰余類の演算 $${\circ}$$ は

$$
\begin{align*}
idN\circ\tau_1N&\hspace{-2pt}\underset{def}{=}\hspace{-1pt}id\tau_1N\\
&=\tau_1N　\because (*1) より\\
\\
\rho_2N\circ\tau_3N&\hspace{-2pt}\underset{def}{=}\hspace{-1pt}\rho_2\tau_3N\\
&=\tau_2N　\because (*2) より\\
&=\tau_1N　\because \tau_2N=\tau_1N より
\end{align*}
$$

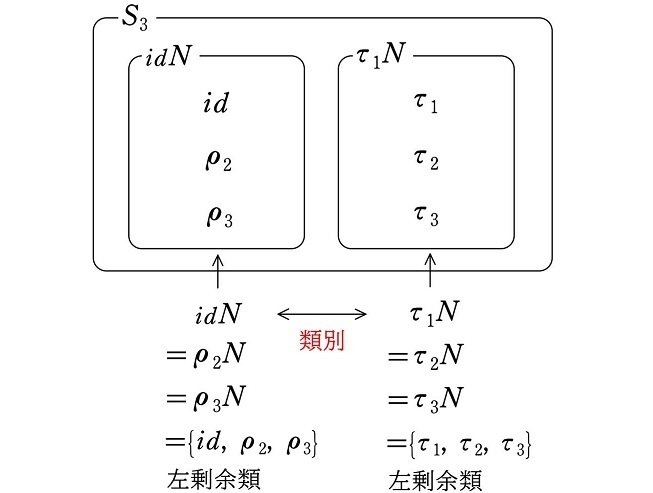
と定まります（「$${\because}$$」は ”なぜなら” を表す記号）。$${\tau_2N=\tau_1N}$$ は、左剰余類による類別によります（図１）。

（図１）

　代表元どうしの積を求め、その新たな代表元の左剰余類をその演算の結果とします。
　なお、この左剰余類の類別（図１）
　$${idN=\rho_2N=\rho_3N}$$
かつ
　$${\tau_1N=\tau_2N=\tau_3N}$$
は、今後頻繁に出てくるので押さえておいてください。覚えてしまった方がよいかもしれません。

well-defined な定義について

　なお、先ほどの左剰余類の演算 $${\circ}$$ の定義
　$${aN\circ bN=abN}$$
について注意事項があります。
　それは、この定義が well-defined（ウェル・ディファインド）になっているかどうかです。well-defined とは、平たくいえば、「矛盾がおきることなく、ちゃんと定義されている」ことを意味します。演算を定義する場合、その定義は well-defined でなければなりません。
　具体例を上げて解説します。

well-defined な定義の例

　例えば、分数の足し算は次のように定義されます。

$$
\begin{align*}
\dfrac{b}{a}+\dfrac{d}{c}=\dfrac{bc+ad}{ac}
\end{align*}
$$

いわゆる通分です。この定義より、例えば $${\dfrac{1}{2}+\dfrac{2}{3}}$$ は

$$
\begin{align*}
\dfrac{1}{2}+\dfrac{2}{3}&=\dfrac{1\cdot3+2\cdot2}{2\cdot3}\\
&=\dfrac{7}{6}
\end{align*}
$$

となりますが、$${\dfrac{1}{2}}$$ と同じ値 $${\dfrac{2}{4}\left(=\dfrac{1\times2}{2\times2}\right)}$$、$${\dfrac{2}{3}}$$ と同じ値 $${\dfrac{6}{9}\left(=\dfrac{2\times3}{3\times3}\right)}$$ でこのたし算を行っても

$$
\begin{align*}
\dfrac{2}{4}+\dfrac{6}{9}&=\dfrac{2\cdot9+4\cdot6}{4\cdot9}\\
&=\dfrac{18+24}{36}\\
&=\dfrac{\cancel{42}}{\cancel{36}}\\
&=\dfrac{7}{6}\\
\end{align*}
$$

と、どちらも同じ値となります。これが well-defined な定義です。

$$
\begin{align*}
\\[-14pt]
\dfrac{1}{2}+\dfrac{2}{3}&=\dfrac{7}{6}\\
&\hspace{-40pt}{\scriptsize 同じ}\hspace{-3pt}\updownarrow\hspace{-1pt}{\scriptsize 同じ}\hspace{-3pt}\updownarrow\hspace{15pt}\updownarrow {\footnotesize 同じになる (\textsf{well-defined})}\\
\dfrac{2}{4}+\dfrac{6}{9}&=\dfrac{7}{6}
\end{align*}
$$

well-defined ではない定義の例

　しかし、仮に分数どうしに次のような演算 $${\oplus}$$ を定義したとしましょう。

$$
\begin{align*}
\dfrac{b}{a}\oplus\dfrac{d}{c}=\dfrac{b+d}{a+c}
\end{align*}
$$

あくまでも仮定の計算として、分母は分母どうし、分子は分子どうしで足すと定義します。
　これに従うと、例えば

$$
\begin{align*}
\dfrac{1}{2}\oplus\dfrac{2}{3}=\dfrac{1+2}{2+3}=\dfrac{3}{5}
\end{align*}
$$

となりますが、$${\dfrac{1}{2}}$$ と同じ値 $${\dfrac{2}{4}}$$、$${\dfrac{2}{3}}$$ と同じ値 $${\dfrac{6}{9}}$$ でこの演算 $${\oplus}$$ を行うと

$$
\begin{align*}
\dfrac{2}{4}\oplus\dfrac{6}{9}=\dfrac{2+6}{4+9}=\dfrac{8}{13}
\end{align*}
$$

と、異なる結果となります。同じ値を用いて同じ演算をしたにも関わらず異なる結果となるので、これは well-defined ではありません。

$$
\begin{align*}
\\[-14pt]
\dfrac{1}{2}\oplus\dfrac{2}{3}&=\dfrac{1+2}{2+3}=\dfrac{3}{5}\\
&\hspace{-40pt}{\scriptsize 同じ}\hspace{-3pt}\updownarrow\hspace{-1pt}{\scriptsize 同じ}\hspace{-3pt}\updownarrow\hspace{54pt}\updownarrow {\footnotesize 同じにならない (\textsf{well-defined} ではない)}\\
\dfrac{2}{4}\oplus\dfrac{6}{9}&=\dfrac{2+6}{4+9}=\dfrac{8}{13}
\end{align*}
$$

正規部分群による左剰余類の演算は well-defined か？

　では、正規部分群による左剰余類の演算 $${\circ}$$ の定義

$$
\begin{align*}
aN \circ bN\hspace{-2pt}\underset{def}{=}\hspace{-1pt}abH
\end{align*}
$$

は well-defined になるでしょうか？
　この定義は代表元の取り方に依存しています。これで「左剰余類の演算が定義できる」というためには、同じ左剰余類となる別の代表元を使って演算しても、その結果は同じにならなければなりません。
　やや抽象的なので、具体例を示して解説します。

具体例で解説

　先ほどやった、置換の積の例

$$
\begin{align*}
idN\circ\tau_1N&\hspace{-2pt}\underset{def}{=}\hspace{-1pt}id\tau_1N\\
&=\tau_1N　\because (*1) より\\
&\hspace{12pt}\cdots (*3)
\end{align*}
$$

を考えると、左剰余類による類別

（図１を再掲）

より
　$${idN=\rho_2N(=\rho_3N)}$$
かつ
　$${\tau_1N(=\tau_2N)=\tau_3N}$$
なので、代表元 $${id}$$ を $${\rho_2}$$ にかえた左剰余類 $${\rho_2N}$$ と、代表元 $${\tau_1}$$ を $${\tau_3}$$ にかえた左剰余類 $${\tau_3N}$$ とで同じ演算

$$
\begin{align*}
\rho_2N\circ\tau_3N
\end{align*}
$$

を行っても、$${(*3)}$$ と同じ結果になる必要があります。

（図説）

　実際に演算してみると

$$
\begin{align*}
\rho_2N\circ\tau_3N&=\rho_2\tau_3N\\
&=\tau_2N　\because (*2) より\\
&=\tau_1N　\because \tau_2N=\tau_1N（図１）より
\end{align*}
$$

となり、確かに結果は $${(*3)}$$ と同じになります。

$$
\begin{align*}
&idH\circ\rho_1H=\tau_1H\\
&\hspace{-12pt}{\small 同じ}\hspace{-2pt}\updownarrow\hspace{2pt}{\small 同じ}\hspace{-2pt}\updownarrow\hspace{25pt}\updownarrow{\small 同じになる}\\
&\rho_2H\circ\tau_3H=\tau_1H
\end{align*}
$$

（図説）

　仮にこの結果が異なれば、上で述べた $${\oplus}$$ のように不完全な定義、つまり well-defined ではない定義です。

　一般に、正規部分群による左剰余類どうしの演算
　$${aN\circ bN=abN}$$
は、必ず well-defined な定義になります。
　逆に、正規部分群ではないただの部分群では、この定義は well-defined ではありません（これについては後半の方で解説します）。

　$${aN\circ bN=abN}$$ という演算の定義は、
　$${N}$$ が正規部分群ならば well-defined である
　$${N}$$ が正規部分群でなければ well-defined ではない

　これが、ただの部分群ではだめで、正規部分群でなけらばならない理由です。

　ではここで、３次対称群 $${S_3}$$ のすべての要素 $${a, b}$$ に対して
　$${aN\circ bN}$$
の演算表を完成させることによって、正規部分群 $${N}$$ による左剰余類の演算 $${\circ}$$ の定義が、well-defined であることを具体的に示していきます。

左剰余類の演算が well-defined であることを示す

　３次対称群
　$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
その正規部分群
　$${N=\{id, \rho_2, \rho_3\}}$$
について、$${S_3}$$ のすべての要素に対して
　$${aN\circ bN}$$
の演算表を完成させていきます。
　そのために、$${idN}$$ のグループ
　$${idN=\rho_2N=\rho_3N=\{id, \rho_2, \rho_3\}}$$
と、$${\tau_1N}$$ のグループ
　$${\tau_1N=\tau_2N=\tau_3N=\{\tau_1, \tau_2, \tau_3\}}$$
とで分けて考えます。個別に考えるのではなく、類別された２つのグループごとに、まとめて考えると分かりやすいです。

(1) idHグループどうしの演算表

　$${idH=\rho_2H=\rho_3H}$$ グループどうしで演算 $${\circ}$$ を行います。
　左剰余類の演算 $${\circ}$$ の定義より

　$${idN\circ idN=ididN}$$
　$${idN\circ\rho_2N=id\rho_2N}$$
　$${idN\circ \rho_3N=id\rho_3N}$$

　$${\rho_2N\circ idN=\rho_2idN}$$
　$${\rho_2N\circ\rho_2N=\rho_2\rho_2N}$$
　$${\rho_2N\circ\rho_3N=\rho_2\rho_3N}$$

　$${\rho_3N\circ idN=\rho_3idN}$$
　$${\rho_3N\circ\rho_2N=\rho_3\rho_2N}$$
　$${\rho_3N\circ\rho_3N=\rho_3\rho_3N}$$

これらを表にすると

$$
\def\arraystretch{1.5}
\hspace{46pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|}
\circ & idN& \rho_2N & \rho_3N\\ \hline\hline
idN & ididN & id\rho_2N & id\rho_3N\\ \hline
\rho_2N & \rho_2idN & \rho_2\rho_2N & \rho_2\rho_3N\\ \hline
\rho_3N & \rho_3idN & \rho_3\rho_2N & \rho_3\rho_3N
\end{array}
$$

ここで、$${S_3}$$ の置換の積の演算表

により

　$${idid=id}$$
　$${id\rho_2=\rho_2}$$
　$${id\rho_3=\rho_3}$$

　$${\rho_2id=\rho_2}$$
　$${\rho_2\rho_2=\rho_3}$$
　$${\rho_2\rho_3=id}$$

　$${\rho_3id=\rho_3}$$
　$${\rho_3\rho_2=id}$$
　$${\rho_3\rho_3=\rho_2}$$

なので

　$${idN\circ idN=ididN=idN}$$
　$${idN\circ\rho_2N=id\rho_2N=\rho_2N}$$
　$${idN\circ\rho_3N=id\rho_3N=\rho_3N}$$

　$${\rho_2N\circ idN=\rho_2idN=\rho_2N}$$
　$${\rho_2N\circ\rho_2N=\rho_2\rho_2N=\rho_3N}$$
　$${\rho_2N\circ\rho_3N=\rho_2\rho_3N=idN}$$

　$${\rho_3N\circ idN=\rho_3idN=\rho_3N}$$
　$${\rho_3N\circ\rho_2N=\rho_3\rho_2N=idN}$$
　$${\rho_3N\circ\rho_3N=\rho_3\rho_3N=\rho_2N}$$

これらを表にすると

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idN & \rho_2N & \rho_3N\\ \hline\hline
idN & idN & \rho_2N & \rho_3N\\ \hline
\rho_2N & \rho_2N & \rho_3N & idN\\ \hline
\rho_3N & \rho_3N & idN & \rho_2N
\end{array}
$$

さらに、左剰余類による類別（図１）
　$${idN=\rho_2N=\rho_3N}$$
より結果はすべて同じになるので、次のように結果を $${idN}$$ に選んで

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idN & \rho_2N & \rho_3N\\ \hline\hline
& & \rho_2N & \rho_3N\\[-7pt]
idN & idN & \downarrow & \downarrow\\[-6pt]
& & idN & idN\\ \hline
& \rho_2N & \rho_3N & \\[-7pt]
\rho_2N & \downarrow & \downarrow & idN\\[-6pt]
& idN & idN & \\ \hline
& \rho_3N & & \rho_2N\\[-7pt]
\rho_3N & \downarrow & idN & \downarrow\\[-6pt]
& idN & & idN
\end{array}
$$

よって

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & \tau_1N & \tau_2N & \tau_3N\\ \hline\hline
idN & idN & idN & idN\\ \hline
\rho_2N & idN & idN & idN\\ \hline
\rho_3N & idN & idN & idN
\end{array}
$$

　$${3\times3=9}$$ 通りのすべての結果は、どれも同じ $${idN}$$ になりました。左剰余類の代表元として $${id, \rho_2, \rho_3}$$ のどの組み合わせで演算しても、すべて同じ結果となります。

(2) idH グループと τH グループとの演算表

　(1) と同様に演算表を作っていきます。
　$${idN=\rho_2N=\rho_3N}$$
グループを先に、
　$${\tau_1H=\tau_2H=\tau_3H}$$
グループを後にして演算 $${\circ}$$ を行います。
　左剰余類の演算 $${\circ}$$ の定義より

　$${\overset{先}{idN}\circ\overset{後}{\tau_1N}=id\tau_1N}$$
　$${idN\circ\tau_2N=id\tau_2N}$$
　$${idN\circ\tau_3N=id\tau_3N}$$

　$${\rho_2N\circ\tau_1N=\rho_2\tau_1N}$$
　$${\rho_2N\circ\tau_2N=\rho_2\tau_2N}$$
　$${\rho_2N\circ\tau_3N=\rho_2\tau_3N}$$

　$${\rho_3N\circ\tau_1N=\rho_2\tau_1N}$$
　$${\rho_3N\circ\tau_2N=\rho_3\tau_2N}$$
　$${\rho_3N\circ\tau_3N=\rho_3\tau_3N}$$

これらを表にすると

$$
\def\arraystretch{1.5}
\hspace{46pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|}
\circ & \tau_1N& \tau_2N & \tau_3N\\ \hline\hline
idN & id\tau_1N & id\tau_2N & id\tau_3N\\ \hline
\rho_2N & \rho_2\tau_1N & \rho_2\tau_2N & \rho_2\tau_3N\\ \hline
\rho_3N & \rho_3\tau_1N & \rho_3\tau_2N & \rho_3\tau_3N
\end{array}
$$

ここで、$${S_3}$$ の置換の積の演算表

より

　$${id\tau_1=\tau_1}$$
　$${id\tau_2=\tau_2}$$
　$${id\tau_3=\tau_3}$$

　$${\rho_2\tau_1=\tau_3}$$
　$${\rho_2\tau_2=\tau_1}$$
　$${\rho_2\tau_3=\tau_2}$$

　$${\rho_3\tau_1=\tau_2}$$
　$${\rho_3\tau_2=\tau_3}$$
　$${\rho_3\tau_3=\tau_1}$$

なので

　$${idN\circ\tau_1N=id\tau_1N=\tau_1N}$$
　$${idN\circ \tau_2N=id\tau_2N=\tau_2N}$$
　$${idN\circ \tau_3N=id\tau_3N=\tau_3N}$$

　$${\rho_2N\circ \tau_1N=\rho_2\tau_1N=\tau_3N}$$
　$${\rho_2N\circ \tau_2N=\rho_2\tau_2N=\tau_1N}$$
　$${\rho_2N\circ \tau_3N=\rho_2\tau_3N=\tau_2N}$$

　$${\rho_3N\circ \tau_1N=\rho_3\tau_1N=\tau_2N}$$
　$${\rho_3N\circ \tau_2N=\rho_3\tau_2N=\tau_3N}$$
　$${\rho_3N\circ \tau_3N=\rho_3\tau_3N=\tau_1N}$$

これらを表にすると

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & \tau_1N & \tau_2N & \tau_3N\\ \hline\hline
idN & \tau_1N & \tau_2N & \tau_3N\\ \hline
\rho_2N & \tau_3N & \tau_1N & \tau_2N\\ \hline
\rho_3N & \tau_2N & \tau_3N & \tau_1N
\end{array}
$$

さらに、左剰余類による類別（図１）
　$${\tau_1N=\tau_2N=\tau_3N}$$
より結果はすべて同じになるので、次のように結果を $${\tau_1N}$$ に選んで

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & \tau_1N & \tau_2N & \tau_3N\\ \hline\hline
& & \tau_2N & \tau_3N\\[-7pt]
idN & \tau_1N & \downarrow & \downarrow\\[-7pt]
& & \tau_1N & \tau_1N\\ \hline
& \tau_3N & & \tau_2N\\[-7pt]
\rho_2N & \downarrow & \tau_1N & \downarrow\\[-7pt]
& \tau_1N & & \tau_1N\\ \hline
& \tau_2N & \tau_3N &\\[-7pt]
\rho_3N & \downarrow & \downarrow & \tau_1N\\[-7pt]
& \tau_1N & \tau_1N &
\end{array}
$$

よって

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & \tau_1N & \tau_2N & \tau_3N\\ \hline\hline
idN & \tau_1N & \tau_1N & \tau_1N\\ \hline
\rho_2N & \tau_1N & \tau_1N & \tau_1N\\ \hline
\rho_3N & \tau_1N & \tau_1N & \tau_1N
\end{array}
$$

　$${3\times3=9}$$ 通りのすべての結果は、どれも同じ $${\tau_1N}$$ となりました。先の左剰余類の代表元として $${id, \rho_2, \rho_3}$$、後の左剰余類の代表元として $${\tau_1, \tau_2, \tau_3}$$ のどの組み合わせで演算しても、すべて同じ結果となります。

(3) tH グループと idH グループとの演算表

　(1), (2) と同様なので、ここからは結果のみを演算表を用いて記していきます。
　(2) の演算の順序を逆にします。つまり
　$${\tau_1H=\tau_2H=\tau_3H}$$
グループを先に、
　$${idH=\rho_2H=\rho_3H}$$
グループを後にして演算 $${\circ}$$ を行います。
　左剰余類の演算 $${\circ}$$ の定義より

$$
\def\arraystretch{1.5}
\hspace{46pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idN & \rho_2N & \rho_3N\\ \hline\hline
\tau_1N & \tau_1idN & \tau_1\rho_2N & \tau_1\rho_3N\\ \hline
\tau_2N & \tau_2idN & \tau_2\rho_2N & \tau_2\rho_3N\\ \hline
\tau_3N & \tau_3idN & \tau_3\rho_2N & \tau_3\rho_3N
\end{array}
$$

$${S_3}$$ の置換の積の演算表より

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idN & \rho_2N & \rho_3N\\ \hline\hline
\tau_1N & \tau_1N & \tau_2N & \tau_3N\\ \hline
\tau_2N & \tau_2N & \tau_3N & \tau_1N\\ \hline
\tau_3N & \tau_3N & \tau_1N & \tau_2N
\end{array}
$$

左剰余類による類別（図１）
　$${\tau_1H=\tau_2H=\tau_3H}$$
より結果はすべて同じになるので、次のように結果を $${\tau_1N}$$ に選んで

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idN & \rho_2N & \rho_3N\\ \hline\hline
& & \tau_2N & \tau_3N\\[-7pt]
\tau_1N & \tau_1N & \downarrow & \downarrow\\[-7pt]
& & \tau_1N & \tau_1N\\\hline
& \tau_2N & \tau_3N & \\[-7pt]
\tau_2N & \downarrow & \downarrow & \tau_1N\\[-7pt]
& \tau_1N & \tau_1N & \\ \hline
& \tau_3N & & \tau_2N\\[-7pt]
\tau_3N & \downarrow & \tau_1N & \downarrow\\[-7pt]
& \tau_1N & & \tau_1N
\end{array}
$$

よって

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idN & \rho_2N & \rho_3N\\ \hline\hline
\tau_1N & \tau_1N & \tau_1N & \tau_1N\\ \hline
\tau_2N & \tau_1N & \tau_1N & \tau_1N\\ \hline
\tau_3N & \tau_1N & \tau_1N & \tau_1N
\end{array}
$$

　$${3\times3=9}$$ 通りのすべての結果は、どれも同じ $${\tau_1N}$$ となりました。先の左剰余類の代表元として $${\tau_1, \tau_2, \tau_3}$$、後の左剰余類の代表元として $${id, \rho_2, \rho_3}$$ のどの組み合わせで演算しても、すべて同じ結果となります。

(4) tH グループどうしの積の演算表

　$${\tau_1H=\tau_2H=\tau_3H}$$ グループどうしで演算 $${\circ}$$ を行います。
　左剰余類の演算 $${\circ}$$ の定義より

$$
\def\arraystretch{1.5}
\hspace{46pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & \tau_1N & \tau_2N & \tau_3N\\ \hline\hline
\tau_1N & \tau_1\tau_1N & \tau_1\tau_2N & \tau_1\tau_3N\\ \hline
\tau_2N & \tau_2\tau_1N & \tau_2\tau_2N & \tau_2\tau_3N\\ \hline
\tau_3N & \tau_3\tau_1N & \tau_3\tau_2N & \tau_3\tau_3N
\end{array}
$$

$${S_3}$$ の置換の積の演算表より

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & \tau_1N & \tau_2N & \tau_3N\\ \hline\hline
\tau_1N & idN & \rho_2N & \rho_3N\\ \hline
\tau_2N & \rho_3N & idN & \rho_2N\\ \hline
\tau_3N & \rho_2N & \rho_3N & idN
\end{array}
$$

左剰余類による類別（図１）
　$${idH=\rho_2H=\rho_3H}$$
より結果はすべて同じになるので、次のように結果を $${idN}$$ に選んで

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & \tau_1N & \tau_2N & \tau_3N\\ \hline\hline
& & \rho_2N & \rho_3N\\[-7pt]
\tau_1N & idN & \downarrow & \downarrow\\[-6pt]
& & idN & idN\\ \hline
& \rho_3N & & \rho_2N\\[-7pt]
\tau_2N & \downarrow & idN & \downarrow\\[-6pt]
& idN & & idN\\ \hline
& \rho_2N & \rho_3N &\\[-7pt]
\tau_3N & \downarrow & \downarrow & idN\\[-6pt]
& idN & idN &
\end{array}
$$

よって

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & \tau_1N & \tau_2N & \tau_3N\\ \hline\hline
\tau_1N & idN & idN & idN\\ \hline
\tau_2N & idN & idN & idN\\ \hline
\tau_3N & idN & idN & idN
\end{array}
$$

　$${3\times3=9}$$ 通りのすべての結果は、どれも同じ $${idN}$$ となりました。左剰余類の代表元として $${\tau_1, \tau_2, \tau_3}$$ のどの組み合わせで演算しても、すべて同じ結果となります。

　以上をまとめると、(1) の場合、演算結果はすべて $${idN}$$ と同じ結果となります。

(2) の場合、演算結果はすべて $${\tau_1N}$$ と同じ結果となります。

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & \tau_1N & \tau_2N & \tau_3N\\ \hline\hline
idN & \tau_1N & \tau_1N & \tau_1N\\ \hline
\rho_2N & \tau_1N & \tau_1N & \tau_1N\\ \hline
\rho_3N & \tau_1N & \tau_1N & \tau_1N
\end{array}
$$

(3) の場合、演算結果はすべて $${\tau_1N}$$ と同じ結果となります。

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idN & \rho_2N & \rho_3N\\ \hline\hline
\tau_1N & \tau_1N & \tau_1N & \tau_1N\\ \hline
\tau_2N & \tau_1N & \tau_1N & \tau_1N\\ \hline
\tau_3N & \tau_1N & \tau_1N & \tau_1N
\end{array}
$$

(4) の場合、演算結果はすべて $${\tau_1N}$$ と同じ結果となります。

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c}
\circ & idN & \rho_2N & \rho_3N\\ \hline\hline
\tau_1N & \tau_1N & \tau_1N & \tau_1N\\ \hline
\tau_2N & \tau_1N & \tau_1N & \tau_1N\\ \hline
\tau_3N & \tau_1N & \tau_1N & \tau_1N
\end{array}
$$

　以上により、同じ左剰余類となる別の代表元を使って演算しても、その結果は同じになるので、左剰余類の演算
　$${aH\circ bH\hspace{-2pt}\underset{def}{=}\hspace{-1pt}abH}$$
は well-defined であることが分かりました。

演算結果の簡略化

　ここで、(1) ～ (4) の結果を１つの表にまとめると

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c||c|c|c}
\circ & idN & \rho_2N & \rho_3N & \tau_1N & \tau_2N & \tau_3N\\ \hline\hline
idN & idN & idN & idN & \tau_1N & \tau_1N & \tau_1N\\ \hline
\rho_2N & idN & idN & idN & \tau_1N & \tau_1N & \tau_1N\\ \hline
\rho_3N & idN & idN & idN & \tau_1N & \tau_1N & \tau_1N\\ \hline\hline
\tau_1N & \tau_1N & \tau_1N & \tau_1N & idN & idN & idN\\ \hline
\tau_2N & \tau_1N & \tau_1N & \tau_1N & idN & idN & idN\\ \hline
\tau_3N & \tau_1N & \tau_1N & \tau_1N & idN & idN & idN
\end{array}
$$

この表から、左上と右下は $${idN}$$、左下と右上が $${\tau_1N}$$ になるので、そのエリアごとに結果をまとめると

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||ccc||ccc}
\circ & idN & \rho_2N & \rho_3N & \tau_1N & \tau_2N & \tau_3N\\ \hline\hline
idN & & & & & & \\
\rho_2N & & idN & & & \tau_1N & \\
\rho_3N & & & & & & \\ \hline\hline
\tau_1N & & & & & &\\
\tau_2N & & \tau_1N & & & idN\\
\tau_3N & & & & & &
\end{array}
$$

また、左剰余類による類別（図１）
　$${idN=\rho_2N=\rho_3N}$$
　$${\tau_1N=\tau_2N=\tau_3N}$$
より、次のように演算させる左剰余類も $${idN}$$ と $${\tau_1N}$$ でまとめると

$$
\def\arraystretch{1.5}
\hspace{81pt}後\\
\raisebox{4pt}{先}\hspace{4pt}
\begin{array}{c||ccc||ccc}
& & \rho_2N & \rho_3N & & \tau_2N & \tau_3N\\[-7pt]
\circ & idN & \downarrow & \downarrow & \tau_1N & \downarrow & \downarrow\\[-6pt]
& & idN & idN & & \tau_1N & \tau_1N\\ \hline\hline
idN & & & & & & \\
\rho_2N\hspace{-2pt}\rightarrow\hspace{-1pt}idN & & idN & & & \tau_1N & \\
\rho_3N\hspace{-2pt}\rightarrow\hspace{-1pt}idN & & & & & & \\ \hline\hline
\tau_1N & & & & & &\\
\tau_2N\hspace{-2pt}\rightarrow\hspace{-1pt}\tau_1N & & \tau_1N & & & idN\\
\tau_3N\hspace{-2pt}\rightarrow\hspace{-1pt}\tau_1N & & & & & &
\end{array}
$$

より

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||ccc||ccc}
\circ & idN & idN & idN & \tau_1N & \tau_1N & \tau_1N\\ \hline\hline
idN & & & & & & \\
idN & & idN & & & \tau_1N & \\
idN & & & & & & \\ \hline\hline
\tau_1N & & & & & &\\
\tau_1N & & \tau_1N & & & idN\\
\tau_1N & & & & & &
\end{array}
$$

となるので、これをシンプルにまとめると次のようになります。

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & idN & \tau_1N\\ \hline\hline
idN & idN & \tau_1N\\ \hline
\tau_1N & \tau_1N & idN
\end{array}
$$

これは、$${idN}$$ と $${\tau_1N}$$ の、２つの左剰余類の間の演算 $${\circ}$$ の演算表とみることができます。

　以上より、初めは $${6\times6=36}$$ 通りの演算であったものが、左剰余類による類別（図１）
　$${idN=\rho_2N=\rho_3N}$$
　$${\tau_1N=\tau_2N=\tau_3N}$$
によって、$${2\times2=4}$$ 通りの well-defined な演算に簡略化することができます。

（再掲）

$${\hspace{60pt}\downarrow}$$ 簡略化

左剰余類の集合が群になること

　ここから、左剰余類の集合
　$${\{idN, \tau_2N\}}$$
が、演算 $${\circ}$$
　$${aN\circ bN=abN}$$
に関して群になることを示していきます。
　なお、左剰余類の集合は
　$${\{idN, \rho_2N, \rho_3N, \tau_1N, \tau_2N, \tau_3N\}}$$
と表記しないことを注意しておきます。
　集合の表記法として、１つの集合に同じ要素をいくつも書くことはありません。例えば $${\{1, 2, 2, 3\}}$$ は、同じ要素を１つにして $${\{1, 2, 3\}}$$ と表記します。
　すると、左剰余類による類別（図１）
　$${idN=\rho_2N=\rho_3N}$$
　$${\tau_1N=\tau_2N=\tau_3N}$$
により、同じ要素を１つにして $${\{idN, \tau_1N\}}$$ と表したものが左剰余類の集合です。ここでは $${idN}$$ と $${\tau_1N}$$ を代表として選んでいます。

$$
\begin{gather*}
\{\underset{idN}{\underline{idN, \rho_2N, \rho_3N}}, \underset{\tau_1N}{\underline{\tau_1N, \tau_2N, \tau_3N}\}}\\
\downarrow\\
\{idN, \tau_1N\}
\end{gather*}
$$

　さて、群になるためには、次の２つの条件が必要です。

➀　演算 $${\circ}$$ が well-defined であること。
②　群の定義を満たすこと。

　➀ は先ほど確認しました。よって、ここでは ② を示していきます。
　まず、群の定義を復習します。

群の定義（復習）

＊＊＊

　$${\{idN, \tau_1N\}}$$ が、左剰余類の演算 $${\circ}$$ に関して群の定義 (1) ～ (4) をすべて満たすことを証明していきます。

(1)　演算に関して閉じている。

　先ほどの演算表

より
　$${idN\circ idN=idH}$$
　$${idN\circ\tau_1N=\tau_1N}$$
　$${\tau_1N\circ idN=\tau_1N}$$
　$${\tau_1N\circ\tau_1N=idN}$$
となるので、$${2\times2=4}$$ 通りの結果はすべて $${\{idN, \tau_1N\}}$$ の要素となり、(1) を満たします。$${\{idN, \tau_1N\}}$$ は左剰余類の演算 $${\circ}$$ について閉じています。

(2)　結合法則は成り立つ。

　例えば、次の交換法則は成り立ちます。
　$${(\tau_1N\circ idN)\circ\tau_1N=\tau_1N\circ(idN\circ\tau_1N)}$$
以下、この式を証明します。
（証明）
　左剰余類の演算 $${\circ}$$ の定義
　$${aN\circ bN=abN}$$
より
　$${(\tau_1N\circ idN)\circ\tau_1N=(\tau_1idH)\circ\tau_1N=\underline{(\tau_1 id)\tau_1}N　\cdots (*1)}$$
　$${\tau_1N\circ(idN\circ\tau_1N)=\tau_1N\circ(id\tau_1N)=\underline{\tau_1(id\tau_1)}N　\cdots (*2)}$$
　ここで、$${\{id, \tau_1\}}$$ は３次対称群 $${S_3}$$ の部分群であるので、$${\{id, \tau_1\}}$$ はそもそも群です。つまり、$${\{id, \tau_1\}}$$ の任意の要素について、交換法則は常に成り立つので
　$${(\tau_1 id)\tau_1=\tau_1(id\tau_1)}$$
すると、$${(*1), (*2)}$$ の下線部は等しくなるので
　$${(*1)=(*2)}$$
より、次の交換法則
　$${(\tau_1N\circ idN)\circ\tau_1N=\tau_1N\circ(idN\circ \tau_1N)}$$
は成り立つことが分かります。
　このような理由で、一般にどのような順序でも交換法則は成り立つので、(2) を満たします。

(3)　単位元は存在する。

　演算表

より
　$${\tau_1N\circ\underline{idN}=\underline{idN}\circ\tau_1N=\tau_1N}$$（変化しない）
が成り立つので、単位元は $${\underline{idH}}$$ です。よって、単位元は $${\{idN, \tau_1N\}}$$ の要素として存在するので、(3) を満たします。

(4)　逆元は存在する。

　$${idN\circ\underline{idN}=\underline{idN}\circ idN=idN}$$（単位元）
　$${\tau_1N\circ\underline{\tau_1N}=\underline{\tau_1N}\circ\tau_1N=idN}$$（単位元）
より、$${idN}$$ の逆元は $${\underline{idN}}$$、$${\tau_1N}$$ の逆元は $${\underline{\tau_1N}}$$ です。よって、逆元は $${\{idN, \tau_1N\}}$$ の要素として存在するので、(4) を満たします。

　以上により、群の定義 (1) ～ (4) をすべて満たすので、正規部分群 $${N}$$ による左剰剰余類の集合 $${\{idN, \tau_1N\}}$$ は

$$
\begin{align*}
aN \circ bN\hspace{-2pt}\underset{def}{=}\hspace{-1pt}abH
\end{align*}
$$

という演算 $${\circ}$$ に関して群になることが証明されました。

　この群 $${\{idN, \tau_1N\}}$$ を、$${S_3}$$ の $${N}$$ による『剰余群』といいます。

剰余群の定義

　剰余群について、改めて定義すると次にようになります。ちょうど、これまでの内容のまとめになります。

＜剰余群の定義＞
　$${N}$$ を群 $${G}$$ の部分群とする。$${G}$$ のすべての要素 $${g}$$ について
　$${gN=Ng}$$
を満たすとき、$${N}$$ を $${G}$$ の『正規部分群』という。

　また、$${N}$$ が $${G}$$ の正規部分群であるとき、$${N}$$ による左剰余類の集合は、$${G}$$ のすべての要素 $${a, b}$$ について
　$${aN\circ bN=abN}$$
という演算 $${\circ}$$ に関して群になる。
　この群を $${G}$$ の $${N}$$ による『剰余群』という。

＊＊＊

　３次対称群
　$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
は群です。その正規部分群 $${N=\{id, \rho_2, \rho_3\}}$$ を考えたとき、その左剰余類による類別
　$${\{idN, \tau_1N\}}$$
も群となります。いわば群構造のなかに群構造が現れます。群構造が入れ子状になっているわけです。

$$
\begin{gather*}
\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\} は群\\
\hspace{2pt}\downarrow {\small 類別}\\
\{idN, \tau_1N\} は群
\end{gather*}
$$

　これが、ガロアの偉大なる発見であり、「５次以上の方程式に解の公式が存在しないこと」への決定的な役割を演じます。

（追記）

　なお、左剰余類の集合 $${\{idN, \tau_1N\}}$$ は、「集合を要素に持つ集合」であることに注意してください。$${\{idN, \tau_1N\}}$$ の要素は $${idN, \tau_1N}$$ ですが、それは
　$${idN=\{id, \rho_2, \rho_3\}}$$
　$${\tau_1N=\{\tau_1, \tau_2, \tau_3\}}$$
という集合でした。すなわち、左剰余類の集合は
　$${\{idN, \tau_1N\}=\{\{id, \rho_2, \rho_3\}, \{\tau_1, \tau_2, \tau_3\}\}}$$
という「集合を要素に持つ集合」となります。

$$
\{idN, \tau_1N\}=\{\underset{要素が集合}{\underline{\{id, \rho_2, \rho_3\}}}, \underset{要素が集合}{\underline{\{\tau_1, \tau_2, \tau_3\}}}\}
$$

　つまり、３次対称群
　$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
は群であり、その正規部分群
　$${N=\{id, \rho_2, \rho_3\}}$$
によって類別された左剰余類の集合
　$${\{idN, \tau_1N\}=\{\{id, \rho_2, \rho_3\}, \{\tau_1, \tau_2, \tau_3\}\}}$$
について、その要素である
　$${idN=\{id, \rho_2, \rho_3\}}$$
　$${\tau_1N=\{\tau_1, \tau_2, \tau_3\}}$$
という「集合」が、$${aN\circ bN=abN}$$ という演算に関して「一体」となって群（剰余群）となる、というのがガロアの発見であり、正規部分群が重要である理由です。

$$
\begin{align*}
&\hspace{43.8pt}\underline{\footnotesize \hspace{16.6pt}剰余群\hspace{16.5pt}}\\[-6pt]
\{idN, \tau_1N\}&=\{\overset{\downarrow}{\underset{idN}{\underline{\{id, \rho_2, \rho_3\}}}}, \overset{\downarrow}{\underset{\tau_1N}{\underline{\{\tau_1, \tau_2, \tau_3\}}}}\}
\end{align*}
$$

（追記終わり）

正規部分群ではない場合

　それでは、正規部分群ではない場合はどうなるか。
　結論からいうと、仮に $${N}$$ を正規部分群ではない部分群とした場合、次の演算 $${\circ}$$ の定義

$$
\begin{align*}
aN \circ bN\hspace{-2pt}\underset{def}{=}\hspace{-1pt}abN
\end{align*}
$$

は well-defined ではありません。この定義が well-defined になるのは、$${N}$$ が正規部分群のときのみとなります。
　例えば、本シリーズ (30) で、$${S_3}$$ の正規部分群ではない部分群として
　$${M=\{id, \tau_1\}}$$
を取り上げました。この部分群による左剰余類で $${S_3}$$ を分類すると、次のようになります（本シリーズ (30)）。

（図２）

　ここで、左剰余類の演算 $${\circ}$$ の定義に従って
　$${idM\circ\rho_2M}$$
　$${\tau_1M\circ\tau_3M}$$
を計算します。（図２）より、$${idM=\tau_1M}$$ かつ $${\rho_2M=\tau_3M}$$ なので、 well-defined であれば、両者は同じ結果になるはずです。

$$
\begin{align*}
&idM\circ\rho_2M=id\rho_2M\\
&\hspace{-12pt}{\small 同じ}\hspace{-2pt}\updownarrow\hspace{4pt}{\small 同じ}\hspace{-2pt}\updownarrow\hspace{30pt}\updownarrow{\small \textsf{well-defined} であれば同じ結果}\\
&\tau_1M\circ\tau_3M=\tau_1\tau_3M
\end{align*}
$$

　すると、$${S_3}$$ の置換の積の対応表

$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
& id & \underline{\rho_2} & \rho_3 & \tau_1 & \tau_2 & \utilde{\tau_3}\\ \hline\hline
\underline{id} & id & \underline{\rho_2} & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline
\rho_2 & \rho_2 & \rho_3 & id & \tau_3 & \tau_1 & \tau_2\\ \hline
\rho_3 & \rho_3 & id & \rho_2 & \tau_2 & \tau_3 & \tau_1\\ \hline
\utilde{\tau_1} & \tau_1 & \tau_2 & \tau_3 & id & \rho_2 & \utilde{\rho_3}\\ \hline
\tau_2 & \tau_2 & \tau_3 & \tau_1 & \rho_3 & id & \rho_2\\ \hline
\tau_3 & \tau_3 & \tau_1 & \tau_2 & \rho_2 & \rho_3 & id
\end{array}
$$

より
　$${id\rho_2=\rho_2}$$（下線部）
　$${\tau_1\tau_3=\rho_3}$$（波線部）
なので

$$
\begin{align*}
&idM\circ\rho_2M=\rho_2M\\
&\hspace{-12pt}{\small 同じ}\hspace{-2pt}\updownarrow\hspace{4pt}{\small 同じ}\hspace{-2pt}\updownarrow\\
&\tau_1M\circ\tau_3M=\rho_3M
\end{align*}
$$

となりますが

$$
\begin{align*}
\rho_2M\ne\rho_3M
\end{align*}
$$

より演算結果は同じにならないので（図２）、正規部分群ではない $${M}$$ による左剰余類については、演算

$$
\begin{align*}
aM \circ bM\hspace{-2pt}\underset{def}{=}\hspace{-1pt}abM
\end{align*}
$$

は well-defined にはなりません。

$$
\begin{align*}
&idM\circ\rho_2M=\rho_2M\\
&\hspace{-12pt}{\small 同じ}\hspace{-2pt}\updownarrow\hspace{3pt}{\small 同じ}\hspace{-2pt}\updownarrow\hspace{26pt}\updownarrow{\footnotesize 同じ結果にならない(\textsf{well-defined} ではない)}\\
&\tau_1M\circ\tau_3M=\rho_3M
\end{align*}
$$

　すると、この演算はそもそも well-defined ではないので、$${M}$$ はその演算 $${\circ}$$ に関して群とはならないことも合わせて結論されます。演算自体がきちんと定義されていないので、そもそも群構造は持ちません。

　一般に、左剰余類の集合が演算 $${\circ}$$ に関して群になるのは、正規部分群による左剰余類の場合のみとなります。

　$${aN\circ bN=abN}$$ という演算に関して、
　$${N}$$ が正規部分群ならば、左剰余類の集合は群になる
　$${N}$$ が正規部分群でないなら、左剰余類の集合は群にならない

右剰余類の集合も群になること

　ここまでは左剰余類について述べてきましたが、一般に、正規部分群による右剰余類の場合でも、次の演算 $${\circ}$$ の定義

$$
\begin{align*}
Na \circ Nb\hspace{-2pt}\underset{def}{=}\hspace{-1pt}Nab
\end{align*}
$$

は well-defined となります。
　また、正規部分群による右剰余類の集合は、この演算 $${\circ}$$ に関して群となります。左剰余類のときと同様、正規部分群であることが重要です。

　$${Na\circ Nb=Nab}$$ という演算に関して、
　$${N}$$ が正規部分群ならば、右剰余類の集合は群になる
　$${N}$$ が正規部分群でないなら、右剰余類の集合は群にならない

　正規部分群 $${N}$$ の定義 $${aN=Na}$$ により、正規部分群であれば左剰余類と右剰余類は一致するので、左剰余類で行った議論を、右剰余類でも同様に行うことが可能です。左か右か、どちらかで統一して議論すればよいことになります。本記事では左剰余類で統一して議論しました。
　改めて右剰余類を用いて剰余群を定義すると、次のようになります。

　また、$${N}$$ が $${G}$$ の正規部分群であるとき、$${G}$$ の $${N}$$ による右剰余類の集合は、$${G}$$ のすべての要素 $${a, b}$$ について
　$${Na\circ Nb=Nab}$$
という演算 $${\circ}$$ に関して群になる。
　この群を $${G}$$ の $${N}$$ による『剰余群』という。

＊＊＊

まとめ

　本記事で述べた、「正規部分群による剰余類の集合は、その剰余類どうしに演算 $${\circ}$$ を定義することによって群となる」というのがガロアの偉大な発見であり、これが「５次以上の方程式に解の公式が存在しないこと」への決定的な役割を演じます。
　この事実を用いて、次の章から「５次以上の方程式に解の公式が存在しない」ガロアの証明のアイデアをみていきます。

（参考）各章の内容

（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となること、及び「差積」と平方根を結ぶ等式の証明。
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式が存在するのか」を解説（添加する式について加筆予定）
（12）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（前編）。「差積の２乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む（対称性の破壊）。
（13）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（後編）。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む（対称性の破壊）。$${\longrightarrow}$$ ３次方程式の解の公式の完成
（14）「アーベルの証明」の解説①。５次方程式の解の差積（または差積の２乗の平方根）を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が５次置換（対称式）から遇置換シンメトリーへと破壊されることを解説。
（15）「アーベルの証明」の解説②。すべての置換は互換で表せることから、５次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
（16）「アーベルの証明」の解説➂。「すべての遇置換は３次巡回置換の積で表される」ことの解説。
（17）「アーベルの証明」の解説➃（最後）。「任意の３次巡回置換が５次巡回置換の積で表せる」ことによって、５次方程式には解の公式が存在しないことが証明されることの解説。
（18）もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
（19）もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
（20）もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
（21）もっと分かりやすくシリーズ➃　何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
（22）もっと分かりやすくシリーズ➄「解の和と差の連立」による２次方程式の解の公式の導出について。
（23）もっと分かりやすくシリーズ➅「対称式ではない解の公式を基本対称式で表す」ことのついて。
（24）もっと分かりやすくシリーズ➆「定数 $${\bm{\omega}}$$」について復習
（25）もっと分かりやすくシリーズ➇　３次方程式の解の公式の導出方法「カルダノの方法」を復習
（26）もっと分かりやすくシリーズ➈「カルダノの方法」と「対称性の破壊」の関連について
（27）もっと分かりやすくシリーズ⑩　そもそもなぜ解の公式が存在しないかを『巡回置換』から紐解く
（28）中学でも分かるガロアの証明①　ガロアの発見した「群」について
（29）中学でも分かるガロアの証明②　ガロアの発見した「部分群」について
（30）中学でも分かるガロアの証明③　ガロアの発見した「正規部分群」について

この記事が参加している募集

#数学がすき

3,171件

この記事が気に入ったらサポートをしてみませんか？

（追記有り）中学でも分かるガロアの証明➃『剰余群』について

（復習）群の定義

（復習）部分群の定義

（復習）正規部分群の定義

（復習）正規部分群による類別

剰余類どうしに演算を定義

左剰余類どうしの演算の定義

well-defined な定義について

well-defined な定義の例

well-defined ではない定義の例

正規部分群による左剰余類の演算は well-defined か？

具体例で解説

左剰余類の演算が well-defined であることを示す

(1) idHグループどうしの演算表

(2) idH グループと τH グループとの演算表

(3) tH グループと idH グループとの演算表

(4) tH グループどうしの積の演算表

演算結果の簡略化

左剰余類の集合が群になること

(1) 演算に関して閉じている。

(2) 結合法則は成り立つ。

(3) 単位元は存在する。

(4) 逆元は存在する。

剰余群の定義

（追記）

正規部分群ではない場合

右剰余類の集合も群になること

まとめ

（参考）各章の内容

この記事が参加している募集

(1)　演算に関して閉じている。

(2)　結合法則は成り立つ。

(3)　単位元は存在する。

(4)　逆元は存在する。