
中学でも分かるガロアの証明➁『部分群』について
前回(本シリーズ (28))では『集合』と『群』を説明しました。ここでは『部分集合』と『部分群』について解説していきます。
前回、3次置換全体の集合
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
は、置換の積(合成)という演算に関して群となることを解説しました。この集合 $${S_3}$$ を『3次対称群』といいます。
(再掲)3次対称群の要素
$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=I=id(=\rho_1)\\
\\
➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha \gamma \beta)
=\rho_2\\
\\
➂\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha \beta \gamma)
=\rho_3
\end{rcases}遇置換\\
\\
&\begin{rcases}
➃\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}=\tau_1\\
\\
➄\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}=\tau_2\\
\\
➅\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}=\tau_3
\end{rcases}奇置換
\end{align*}
$$
これらを三角形の図形の移動でとらえると


①~③は回転、④~➅は反転と、2つに分けることができます。
ここからは『部分集合』、『部分群』について解説していきます。
部分集合について
例えば、2つの集合
$${\text{P}=\{2, 4\}}$$
$${\text{Q}=\{1, 2, 3, 4, 5\}}$$
では、どの $${\text{P}}$$ の要素もまた $${\text{Q}}$$ の要素になっています。つまり
$${\text{P}}$$ の要素 $${2}$$ は $${\text{Q}}$$ の要素になっている。
$${\text{P}}$$ の要素 $${4}$$ は $${\text{Q}}$$ の要素になっている。
この2つの集合の関係を図で描くと、次のようになります。

このように、集合が表す範囲を視覚的に表したものを『ベン図』といいます。
一般に、2つの集合 $${\text{A}}$$、$${\text{B}}$$ において、$${\text{A}}$$ のどの要素もまた $${\text{B}}$$ の要素であるとき、すなわち
$$
\begin{align*}
x \in\text{A} ならば x \in\text{B}
\end{align*}
$$
が成り立つとき、A は B に含まれる、または B は A を含むといいます。

また、$${\text{A}}$$ が $${\text{B}}$$ に含まれることを、記号で次のように書きます。
$$
\begin{align*}
\text{A}\subset\text{B} または \text{B}\supset\text{A}
\end{align*}
$$
このとき、$${\text{A}}$$ は $${\text{B}}$$ の『部分集合』といいます。大きい方に開いていると覚えます。2つの集合の一方が他方の部分集合であるとき、この2つの集合の間に包含関係があるといいます。

先ほどの集合
$${\text{P}=\{2, 4\}}$$
$${\text{Q}=\{1, 2, 3, 4, 5\}}$$
の例でいえば、P は Q に含まれるので
$$
\begin{align*}
\text{P}\subset\text{Q} または \text{Q}\supset\text{P}
\end{align*}
$$
が成り立ちます。
(再掲)

なお、同じ集合 $${\text{A}}$$ に対して
$$
\begin{align*}
x \in\text{A} ならば x \in\text{A}
\end{align*}
$$
が成り立つので、$${\text{A}}$$ 自身も $${\text{A}}$$ の部分集合、つまり
$$
\begin{align*}
\text{A}\subset\text{A} または \text{A}\supset\text{A}
\end{align*}
$$
となります。また、$${\text{A}\subset\text{B}}$$ かつ $${\text{B}\subset\text{A}}$$ ならば、$${\text{A}}$$ と $${\text{B}}$$ はその要素がまったく一致して
$$
\begin{align*}
\text{A}=\text{B}
\end{align*}
$$
となります。
さて、整数全体の集合 $${\mathbb{Z}}$$ を要素を並べて書くと、次のようになります。
$$
\begin{align*}
\mathbb{Z}=\{\cdots, -3. -2. -1, 0, 1, 2, 3, \cdots\}
\end{align*}
$$
ここで、自然数全体の集合を $${\mathbb{N}}$$ を考えます。要素を並べて書くと次のようになります。
$$
\begin{align*}
\mathbb{N}=\{1, 2, 3, 4, 5, \cdots\}
\end{align*}
$$
記号 $${\mathbb{N}}$$ は、Natural number(自然数)の頭文字からきています。
すると、集合 $${\mathbb{N}}$$ は、集合 $${\mathbb{Z}}$$ に含まれていることがわかります。つまり
$$
\begin{align*}
\mathbb{N}\subset\mathbb{Z}
\end{align*}
$$
ベン図で表すと次のようになります。

つまり、集合 $${\mathbb{N}}$$ は、集合 $${\mathbb{Z}}$$ の部分集合です。集合 $${\mathbb{N}}$$ は、集合 $${\mathbb{Z}}$$ に含まれるという包含関係があります。
集合 {1, 2, 3} のすべての部分集合
ここで、集合 $${\{1, 2, 3\}}$$ のすべての部分集合を考えてみましょう。以下の集合が $${\{1, 2, 3\}}$$ の部分集合になります。
$${\phi}$$、$${\{1\}}$$、$${\{2\}}$$、$${\{3\}}$$、
$${\{1, 2\}}$$、$${\{1, 3\}}$$、$${\{2, 3\}}$$、$${\{1, 2, 3\}}$$
$${\phi}$$(ファイ)は空集合を表します。空集合は要素をまったくもたない集合です。空集合 $${\phi}$$ は、どのような集合の部分集合にもなっていると考えます。また、自分自身も部分集合となるので、$${\{1, 2, 3\}}$$ も部分集合です。
さて、整数全体の集合 $${\mathbb{Z}}$$ は、たし算に関して群となることは前回示しました。では、その部分集合である $${\mathbb{N}}$$ も、たし算に関して群になるでしょうか? 前回述べた群の定義 (1)~(4) を満たすかどうかで確認していきます。
まずは。前回やった群の定義の復習です。
群の定義(復習)
空でない集合 $${G}$$ の任意の要素 $${a, b, c}$$ の間に1つの演算 $${*}$$ が規定されているとする。
この集合 $${G}$$ の任意の要素 $${a, b, c}$$ が、その演算 $${*}$$ に関して次の条件を満たすとき、$${G}$$ は演算 $${*}$$ に関して群であるという。
(1) $${a*b}$$ は $${G}$$ の要素である。
(2) 交換法則 $${(a*b)*c=a*(b*c)}$$ が成り立つ。
(3) $${a*e=e*a=a}$$ となる単位元 $${e}$$ が $${G}$$ に存在する。
(4) $${a*x=x*a=e}$$ となる逆元 $${x}$$ が $${G}$$ に存在する。
***
(1) を満たすことを、集合 $${\bm G}$$ は演算 $${\bm *}$$ について閉じているといいます。演算の結果、集合 $${G}$$ からはみ出さないことを意味します。
(2) は、カッコを気にしないで、どこから演算を施してもよいことを保証します。
(3) は、左右どちらから演算を施しても変化しない要素の存在です。その要素を単位元といいます。
(4) は、左右両方から演算を施すと単位元になる要素の存在です。その要素を逆元といいます。
要するに群とは、イメージとして
(1) 全部そろっている
(2) どこからでもつなげることができる
(3) 変えないことができる
(4) 元に戻すことができる
の4つの条件が成り立つ要素の集まり(集合)です。
部分群とは
ある群 $${G}$$ の空でない部分集合 $${H}$$ が同じ演算で群になるとき、その部分集合 $${H}$$ を、 $${G}$$ の『部分群』といいます。
ここで重要なのは、あくまでも「同じ演算で」ということです。もとの群がたし算に関して群となる場合、その部分群もたし算に関して群となります。

たし算に関してℕはℤの部分群か?
さて、整数全体の集合
$$
\begin{align*}
\mathbb{Z}=\{\cdots, -3. -2. -1, 0, 1, 2, 3, \cdots\}
\end{align*}
$$
は、たし算に関して群となることは前回示しました。では、その部分集合である自然数の集合
$$
\begin{align*}
\mathbb{N}=\{1, 2, 3, 4, 5, \cdots\}
\end{align*}
$$
は部分群になるでしょうか。もちろん部分群は「同じ演算」で考えるので、考える演算はたし算です。
では、群の定義 (1)~(4) を順に確認していきます。
(1) 自然数同士を足しても自然数である。
$${2+3=5}$$(自然数)
自然数はたし算について閉じています。
(2) 結合法則は成り立つ。
例 $${(2+3)+5=2+(3+5)}$$
結合法則は常になりたちます。
しかし・・・
(3) 単位元は存在しない。
足しても変化しないのが単位元です。例えば
$${1+e=e+1=1}$$
を考えます。$${1}$$ に足しても変化しないもの、これ満たす $${e}$$ が単位元となりますが、それは自然数の集合には存在しません。計算上では $${e=0}$$ とすれば成り立ちますが、$${0}$$ は自然数ではないので、(3) は満たさないことが分かります。
よって (3) を満たさない(つまり、(1)~(4) のすべてを満たさない)ので、$${\mathbb{N}}$$ はたし算に関して $${Z}$$ の部分群にならないことが示されました。

たし算に関して {-1, 0, 1} はℤの部分群か?
一方、 $${\mathbb{Z}}$$ の部分集合として
$${S=\{-1, 0, 1\}}$$
をとったとき、この集合 $${S}$$ はたし算に関して群になるでしょうか。群の定義 (1)~(4) を順に確認していきます。
(1) $${S}$$ の任意の要素同士を足しても $${S}$$ の要素になる。
すべての要素について確認します。
$${-1+0=-1 \in S}$$
$${0+(-1)=-1 \in S}$$
$${-1+1=0 \in S}$$
$${1+(-1)=0 \in S}$$
$${0+1=1 \in S}$$
$${1+0=1 \in S}$$
より、足したものはすべて $${S}$$ の要素になります。$${S}$$ はたし算について閉じています。
(2) 結合法則は成り立つ。
例 $${(-1+0)+1=-1+(0+1)}$$
結合法則は常に成り立ちます。
(3) 単位元は存在する。
足しても変化しないのが単位元です。
$${-1+\underline{0}=\underline{0}+(-1)=-1}$$(変化しない)
$${\hspace{8pt}0+\underline{0}=\underline{0}+0=0}$$(変化しない)
$${\hspace{8pt}1+\underline{0}=\underline{0}+1=1}$$(変化しない)
より、下線部の $${0}$$ が単位元となります。よって、単位元は $${S}$$ に存在します。
(4) 逆元は存在する。
たして単位元 $${0}$$ になるのが逆元です。
$${-1+\underline{1}=\underline{1}+(-1)=0}$$(単位元)
より、$${-1}$$ の逆元は $${1}$$
$${0+\underline{0}=\underline{0}+0=0}$$(単位元)
より、$${0}$$ の逆元は $${0}$$
$${1+(\underline{-1})=\underline{-1}+1=0}$$(単位元)
より、$${1}$$ の逆元は $${-1}$$
下線部が各々の逆元です。よって、すべての要素に対して逆元は $${S}$$ に存在します。
以上により、群の条件 (1)~(4) をすべて満たしているので
$${S=\{-1, 0 1\}}$$
は、たし算に関して $${Z}$$ の部分群となります。
$${N}$$ も $${S}$$ も $${Z}$$ の部分集合ではありますが、たし算に関して、$${N}$$ は部分群ではなく $${S}$$ は部分群となります。


部分集合であっても、部分群となる場合もあれば、ならない場合もあります。
ここで部分群について補足です。
ある群 $${G}$$ の部分群のうち、最大のものは自分自身 $${G}$$ です。また、最小のものは単位元 $${e}$$ だけからなる群 $${\{e\}}$$ です(注1)。この2つは『自明な部分群』といいます。どんな群にも、この自明な部分群は必ず存在します。自明な部分群以外の部分群を『真部分群』といいます。真部分群があるかないかは群によります。
3次交代群について
さて、3次対称群
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
は置換の積に関して群となりますが、その遇置換だけを集めた部分集合
$${A_3=\{id, \rho_2, \rho_3\}}$$
は、$${S_3}$$ の部分群となるでしょうか。結論からいうと、$${A_3}$$ は $${S_3}$$ の部分群となります。この $${A_3}$$ を『3次交代群』といいます。
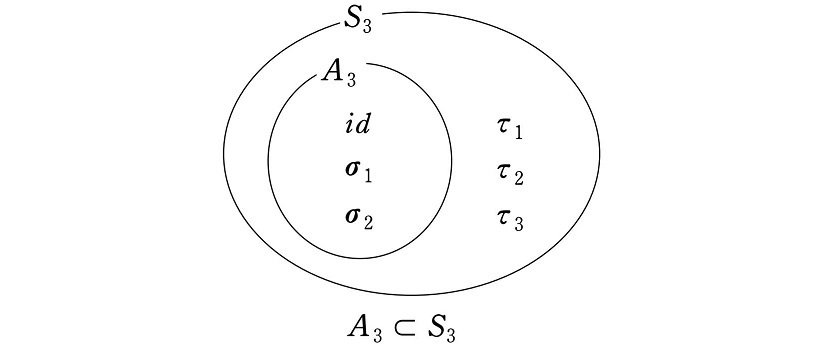
では、この遇置換だけを集めた3次交代群 $${A_3}$$ が、置換の積に関して群の定義 (1)~(4) を満たしていることを確認していきます。
遇置換の集合が部分群になることの証明
(1) 遇置換同士の積は遇置換である。
$${A_3}$$ の任意の2つの要素の積は $${A_3}$$ の要素になります。
$${A_3}$$ の要素は全部で $${3}$$ 通りあるので、その置換の積は全部で $${3\times3=9}$$ 通りありますが、そのすべてが $${A_3}$$ の要素になること、つまり $${A_3}$$ からはみ出さないことを具体的に示していきます。
前回 $${S_3}$$ に対して行ったのと同じ方法なので、ここでは簡潔に書いていきます。
(a) 先に $${id}$$ を作用させると、結果は次のようになります。$${id}$$ は恒等置換なので、いずれも変化しません。
(a1) $${idid=id}$$
(a2) $${id\rho_2=\rho_2}$$
(a3) $${id\rho_3=\rho_3}$$
(a1)~(a3) は、すべて $${A_3}$$ の要素になります。
この結果を表にまとめると、次のようになります。先に作用させる置換を縦に、後に作用させる置換を横に並べています。
$$
\def\arraystretch{1.5}
\hspace{0pt}後\\
\raisebox{-10pt}{先}
\hspace{4pt}
\begin{array}{c||c|c|c}
& id & \rho_2 & \rho_3\\ \hline\hline
id & id & \rho_2 & \rho_3
\end{array}
\begin{array}{c}
\\
← \text{(a)}
\end{array}
$$
(b) 先に $${\rho_2}$$ を作用させると、結果は次のようになります。
(b1) $${\rho_2id=\rho_2}$$
(b2) $${\rho_2\rho_2=\rho_3}$$
(b3) $${\rho_2\rho_3=id}$$
(b1)~(b3) は、すべて $${A_3}$$ の要素になります。
これまでの結果を表にまとめると、次のようになります。先に作用させる置換を縦に、後に作用させる置換を横に並べています。
$$
\def\arraystretch{1.5}
\hspace{0pt}後\\
\raisebox{-10pt}{先}
\hspace{4pt}
\begin{array}{c||c|c|c}
& id & \rho_2 & \rho_3\\ \hline\hline
id & id & \rho_2 & \rho_3\\ \hline
\rho_2 & \rho_2 & \rho_3 & id
\end{array}
\begin{array}{c}
\\
← \text{(a)}\\
← \text{(b)}
\end{array}
$$
(c) 先に $${\rho_3}$$ を作用し、次に3次対称群のすべての要素を作用させると、結果は次のようになります。
(c1) $${\rho_3id=\rho_3}$$
(c2) $${\rho_3\rho_2=id}$$
(c3) $${\rho_3\rho_3=\rho_2}$$
(c1)~(c3) は、すべて $${A_3}$$ の要素になります。
これまで結果を表にまとめると、次のようになります。先に作用させる置換を縦に、後に作用させる置換を横に並べています。
$$
\def\arraystretch{1.5}
\hspace{-10pt}後\\
\raisebox{-10pt}{先}
\hspace{4pt}
\begin{array}{c||c|c|c}
& id & \rho_2 & \rho_3\\ \hline\hline
id & id & \rho_2 & \rho_3\\ \hline
\rho_2 & \rho_2 & \rho_3 & id\\ \hline
\rho_3 & \rho_3 & id & \rho_2
\end{array}
\begin{array}{c}
\\
\leftarrow (a)\\
\leftarrow (b)\\
\leftarrow (c)
\end{array}
$$
以上により、$${3\times3=9}$$ 通りのすべてが $${A_3}$$ の要素に含まれることが分かりました。$${A_3}$$ は置換の積について閉じています。
(2) 結合法則は成り立つ。
例 $${(\rho_2id)\rho_3=\rho_2(id\rho_3)}$$
$${(\rho_2id)\rho_2=\rho_2(id\rho_2)}$$
任意の要素に対して成り立つので、同じ要素があっても構いません。
結合法則は常に成り立ちます。
(3) 単位元は存在する。
置換の積で、変化しないのが単位元です。
$${id\underline{id}=\underline{id}id=id}$$(変化しない)
$${\rho_2\underline{id}=\underline{id}\rho_2=\rho_2}$$(変化しない)
$${\rho_3\underline{id}=\underline{id}\rho_3=\rho_3}$$(変化しない)
より、下線部の $${id}$$ が単位元となります。よって、単位元は $${A_3}$$ に存在します。
(4) 逆元は存在する。
置換の積で、単位元 $${id}$$ になるのが逆元です。
$${id}$$ については
$${id\underline{id}=\underline{id}id=id}$$(単位元)
より、$${id}$$ が逆元となります。
$${\rho_2}$$ については
$${\rho_2\underline{\rho_3}=\underline{\rho_3}\rho_2=id}$$(単位元)
より、$${\rho_3}$$ が逆元となります。
$${\rho_3}$$ については
$${\rho_3\underline{\rho_2}=\underline{\rho_2}\rho_3=id}$$(単位元)
より、$${\rho_2}$$ が逆元となります。
下線部が各々の逆元です。よって、すべての要素に対して逆元は $${A_3}$$ に存在します。
置換を回転とみなすと、$${\rho_2}$$ は $${120^\circ}$$ 回転、$${\rho_3}$$ は $${240^\circ}$$ 回転なので、それらを連続して回転させると $${360^\circ}$$ になり、元に戻る($${id}$$ になる)というイメージです。
以上により、群の定義 (1)~(4) をすべて満たしているので、$${A_3}$$ は置換の積に関して群となります。そしてそれは $${S_3}$$ の部分集合であることから、$${A_3}$$ は $${S_3}$$ の部分群となることが示されました。
3次対称群のすべての部分群
先ほど示したのも含めて、置換の積に関して
$${S_3=\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$
の部分群になるものには、全部で以下の6通りがあります。
$${\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}=S_3}$$
$${\{id, \rho_2, \rho_3\}=A_3}$$
$${\{id, \tau_1\}}$$
$${\{id, \tau_2\}}$$
$${\{id, \tau_3\}}$$
$${\{id\}}$$
なお、自分自身 $${S_3}$$ や、要素が単位元だけからなる集合 $${\{id\}}$$ は『自明な部分群』となります。また、自明な部分群以外の部分群は『真部分群』となります。
$${\{id, \rho_2, \rho_3, \tau_1, \tau_2, \tau_3\}}$$(自明な部分群)
$${\{id, \rho_2, \rho_3\}}$$(真部分群)
$${\{id, \tau_1\}}$$(真部分群)
$${\{id, \tau_2\}}$$(真部分群)
$${\{id, \tau_3\}}$$(真部分群)
$${\{id\}}$$(自明な部分群)
群の定義 (3) より、単位元があることは群の条件に必要なので、どの部分群にも単位元 $${id}$$ が含まれます。
ここでは $${\{id, \tau_1\}}$$ について、群の定義 (1)~(4) をすべて満たすことを確認していきます。
(1) $${\{id, \tau_1\}}$$ の要素の積は $${\{id, \tau_1\}}$$ に含まれる。
$${idid=id}$$
$${id\tau_1=\tau_1}$$
$${\tau_1id=\tau_1}$$
$${\tau_1\tau_1=id}$$
より、置換の積はすべて $${\{id, \tau_1\}}$$ に含まれます。$${\{id, \tau_1\}}$$ は置換の積について閉じています。
(2) 結合法則は成り立つ。
例 $${(\tau_1id)\tau_1=\tau_1(id\tau_1)}$$
任意の要素に対して成り立つので、同じ要素があっても構いません。
結合法則は常に成り立ちます。
(3) 単位元は存在する。
$${id\underline{id}=\underline{id}id=id}$$(変化しない)
$${\tau_1\underline{id}=\underline{id}\tau_1=\tau_1}$$(変化しない)
より、下線部の $${id}$$ が単位元となります。
(4) 逆元は存在する。
$${id\underline{id}=\underline{id}id=id}$$(単位元)
より、$${id}$$ の逆元は $${id}$$ です。
$${\tau_1\underline{\tau_1}=\underline{\tau_1}\tau_1=id}$$
より、$${\tau_1}$$ の逆元は $${\tau_1}$$ です。
下線部が各々の逆元となります。
以上により、群の定義 (1)~(4) をすべて満たしているので、$${\{id, \tau_1\}}$$ は部分群となります。他の部分群に対しても、同様にして群であることが証明されます。
まとめ
ここでは『部分群』の解説をしましたが、いよいよ次は、ガロアの証明の核となる『正規部分群』の解説に入ります。部分群のうち、特別な性質をもつ『正規部分群』が、解の公式が存在するかどうかのカギを握ります。次回はそれを解説する予定していきます。
(注1){id} が群になることの証明。
恒等置換のみの集合 $${\{id\}}$$ が、置換の積に関して群の定義 (1)~(4) をすべて満たすことを確認していきます。
(1) $${idid}$$ は $${\{id\}}$$ の要素である。
$${idid=id}$$
より、$${\{id\}}$$ の要素となります。
(2) 結合法則は成り立つ。
例 $${(idid)id=id(idid)}$$
より、結合法則は成り立ちます。
(3) 単位元は存在する。
$${id\underline{id}=\underline{id}id=id}$$(変化しない)
より、下線部の $${id}$$ が単位元となります。
(4) 逆元は存在する。
$${id\underline{id}=\underline{id}id=id}$$(単位元)
より、$${id}$$ の逆元は下線部の $${id}$$ です。
以上により、群の定義 (1)~(4) をすべて満たしているので、恒等置換だけからなる集合 $${\{id\}}$$ は、置換の積に関して群となります。$${id}$$ は単位元なので、$${\{id\}}$$ は単位元だけからなる群です。一般に、単位元だけからなる群は、すべての群の部分群となります。
(参考)各章の内容
(1)「2次方程式の解の公式」を式変形で導出
・平方完成
(2)「3次方程式の解の公式」を導出するための準備
・$${1}$$ の3乗根 $${\omega}$$
(3)「3次方程式の解の公式」を式変形で導出
・チルンハウス変換
(4)「解と係数の関係」と「対称式」の解説
(5)「対称式」を用いた「2次方程式の解の公式」の導出
(6)「解の置換」と「ラグランジュ・リゾルベント」の解説
(7)「ラグランジュ・リゾルベント」による「3次方程式の解の公式」の導出
(8)「遇置換」と「奇置換」の解説(ここから「アーベルの証明」の準備)
(9)「差積の2乗」が対称式となること、及び「差積」と平方根を結ぶ等式の証明。
(10)「平方根」「3乗根」と次々と累乗根を加えていくアイデア
(11)「アーベルの証明」のアイデアを用いて、なぜ「2次方程式の解の公式が存在するのか」を解説(添加する式について加筆予定)
(12)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(前編)。「差積の2乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む(対称性の破壊)。
(13)「アーベルの証明」のアイデアを用いて、なぜ「3次方程式の解の公式が存在するのか」を解説(後編)。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む(対称性の破壊)。$${\longrightarrow}$$ 3次方程式の解の公式の完成
(14)「アーベルの証明」の解説①。5次方程式の解の差積(または差積の2乗の平方根)を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が5次置換(対称式)から遇置換シンメトリーへと破壊されることを解説。
(15)「アーベルの証明」の解説②。すべての置換は互換で表せることから、5次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
(16)「アーベルの証明」の解説➂。「すべての遇置換は3次巡回置換の積で表される」ことの解説。
(17)「アーベルの証明」の解説➃(最後)。「任意の3次巡回置換が5次巡回置換の積で表せる」ことによって、5次方程式には解の公式が存在しないことが証明されることの解説。
(18)もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
(19)もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
(20)もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
(21)もっと分かりやすくシリーズ➃ 何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
(22)もっと分かりやすくシリーズ➄「解の和と差の連立」による2次方程式の解の公式の導出について。
(23)もっと分かりやすくシリーズ➅「対称式ではない解の公式を基本対称式で表す」ことのついて。
(24)もっと分かりやすくシリーズ➆「定数 $${\bm{\omega}}$$」について復習
(25)もっと分かりやすくシリーズ➇ 3次方程式の解の公式の導出方法「カルダノの方法」を復習
(26)もっと分かりやすくシリーズ➈「カルダノの方法」と「対称性の破壊」の関連について
(27)もっと分かりやすくシリーズ⑩ そもそもなぜ解の公式が存在しないかを『巡回置換』から紐解く
(28)中学でも分かるガロアの証明① ガロアの発見した「群」について簡単に解説
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
