
Philosophiæ Naturalis-月と地球とマスターピース、数字273-
はじめに
今回の記事の内容は、前回の記事で書ききれなかったことを紹介しつつ、数や幾何学から読み解ける不思議な符合を見ていきましょうという記事です。
前回の記事を読んでいなくても読み進められるよう綴りましたので、未読の方も、内容をぼんやりとしか覚えていない方も安心して読んで下さいね。
本編に入る前に、友人との会話を紹介します。この友人は私が逆立ちしても遠く及ばないほど勉強熱心な人物です。
その友人と食事をしていた際に「なぜ勉強するのか」について話をしていました。友人は、「例えば「レモン」という物ひとつとっても色々な表現方法がある。勉強していくと会話の引き出しが増えて人生豊かになると思わない?」と話してくれました。
私は勉強について、「面白いと思っていることについて、どんどん探求をしていきたい」という単細胞な考えを持っていたのですが、「表現が増えて人生が豊かになるのも一理あるな」と、帰り道しみじみ思ったことがあります。
このエピソードを紹介して何を伝えたいのかというと、今回の記事を最後まで読んで頂ければ、会話の引き出しが増え、人生が豊かになるかも知れませんよ!というこれまた単細胞な考えで会話を紹介しました。(笑)
あなたは「月や地球、黄金比について何か語って下さい」と言われたらどの様に答えるでしょうか?
私の個人的な考えなのですが、知識と知識が繋がった時の連鎖は記憶に留まりやすいと考えています。もしかしたらこの記事を読んで、新たな発見があるかもしれませんし、知識と知識が繋がる連鎖が起こるかもしれません。
と、自分で自分のハードルを上げてしまいましたが、前書きはこれくらいにして記事本編を見ていきましょう!
ピタゴラスの定理と月と地球
では、前回登場したピタゴラスの定理のおさらいを簡単にしてから不思議な符合の数々を見ていきましょう。
ピタゴラスの定理とは、「直角三角形の三辺の間に成り立つ関係(三位一体)」の定理でしたね。斜辺の長さをcとした時、直角をはさむ二辺をa,bとすると以下のような等式が成り立ちます。
c²=a²+b²
斜辺cの2乗に対し、直角をはさむ二辺a,bの2乗の和は等しいということです。そして直角三角形の二辺の長さがわかっていれば残りの辺の長さも計算できるのがピタゴラスの定理でした。

↓
25=9+16
↓
25=25

また、前回の記事の後半では5:12:13の直角三角形が登場し、1年間にで訪れる満月の回数(12.369回)などを導き出しました。


今回の記事でもピタゴラスの三角に重点を置きつつ、月と地球の不思議な関係を見ていきます。ですが5:12:13とは別の直角三角形です。
月と地球の大きさはとても絶妙で、3³=27から始まるいつもの倍数「27,54,108,216,432,864」のいくつかが見てとれます。(詳しく過去記事にて)

そんな絶妙な大きさの関係の月と地球ですが、実はピタゴラスの三角に当てはめることが出来ます。しかも興味深いことに「1:√Φ:Φ」の黄金比のピタゴラスの三角。
地球の直径を1とした時、月と地球の直径を合わせた値は√Φになります。そして斜辺はΦに。(精度99.9%)

また、月と地球の直径比は2160:7920=3:11ですが、下の画像のように地球の中心に月を配置し、それぞれに外接する正方形を描きます。そして月の正方形から線を地球に外接する正方形の辺までそれぞれ伸ばすと、下の画像のように3:4:5のピタゴラスの三位一体が当てはまります。

地球の中心に月を配置した説明をしましたのでこちらも紹介しましょう。
これまた面白いことに、地球の円周に内接する五角形、その五角形に内接する円、それに内接する正方形、正方形に内接する円とまた内接する三角形、その三角形に内接する円は月の大きさと一致を見せます(3:11)。
月と地球の比率3:11はこの様にしても見出すことが出来るのですが、三角形・四角形・五角形は3:4:5のピタゴラスの定理とも数字の符合を示しています。

ここまで数字や幾何学の符合が揃うと「本当かよ〜」と思って今いますよね。ですが、実際に計算してみても、画像を作る際に作図をしてみてもピッタリそうなっています。
人間が作り出したものではないのに、ここまで計算されつくしたような符合の数々。数や幾何学はまさに「理」そのものです。
そしてダ・ヴィンチの言葉を思い出しつつ、本当によく出来た世界だなと想いを馳せてしまいます。
あらゆるものは、他のあらゆるものと関連する。

ダ・ヴィンチの言葉を引用しましたので、ダ・ヴィンチの作品も絡めて不思議な符合をさらに見ていきましょう。もちろん月と地球、ピタゴラスの三角も関係してきます。
ウィトルウィウス的人体図

上の画像は、ウィトルウィウスが著した『建築について』の記述をもとにレオナルド・ダ・ヴィンチがスケッチしたものです。皆さんも一度は目にしたことがある作品ではないでしょうか?
このウィトルウィウス的人体図には、円と正方形にそれぞれ内接するように人物が描かれています。
その描かれている円と正方形は、面積が等しい関係です。このような等しい円と正方形を作ることを「円の正方形化」と言います。

上の画像を見ていただいてピンときた方がいらっしゃるかも知れません。前回の記事で紹介したヴェシカ・パイシスを用いて円の正方形化を作図することができます。

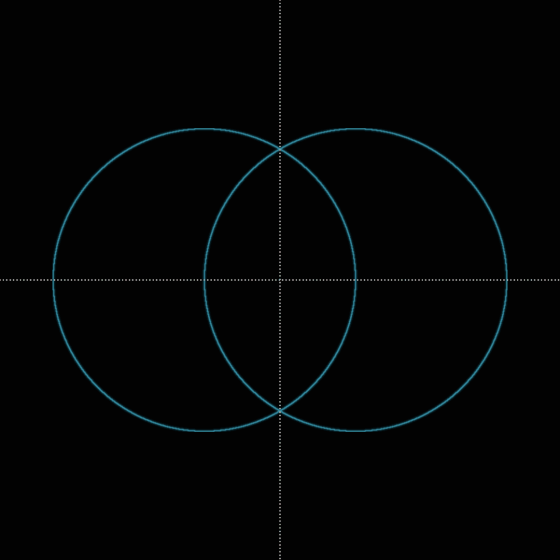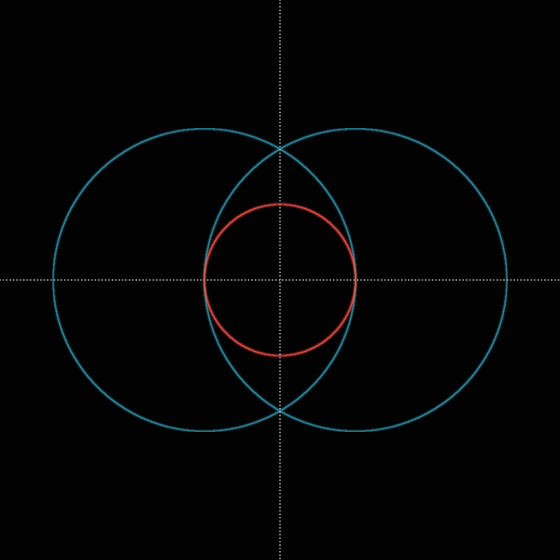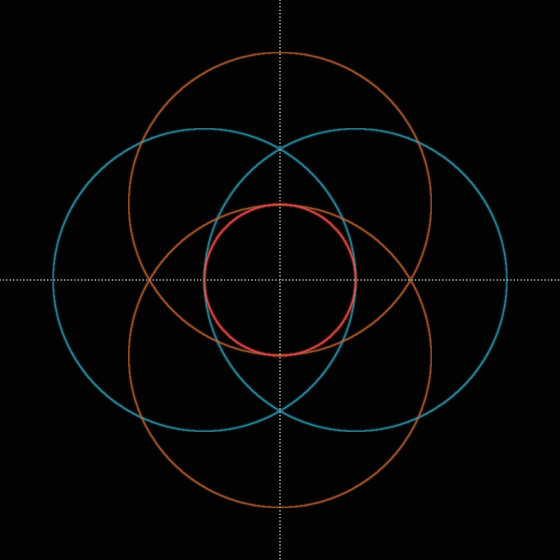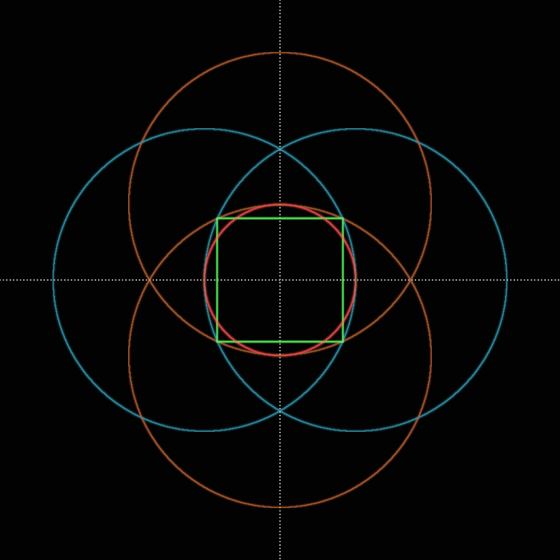
②その円(赤)と垂線の交点を中心点としたヴェシカ・パイシス(青)と同じ大きさのヴェシカ・パイシス(橙)を描く
③青と橙のヴェシカ・パイシスの交点を直線で結ぶと正方形(緑)が作図できる
円(赤)と正方形(緑)の面積は等しい(円の正方形化)
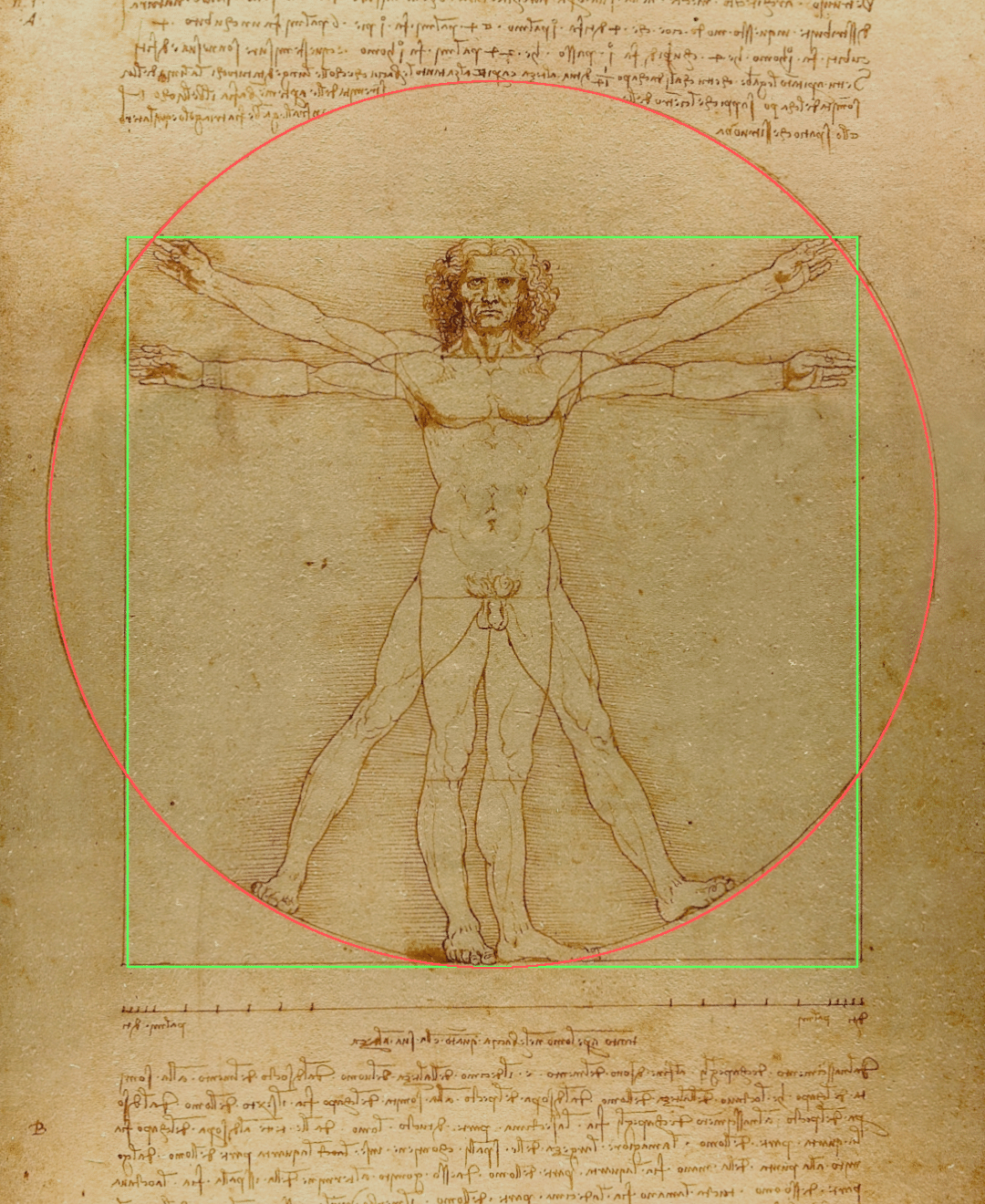
説明はこれくらいにして符合を見てみましょう。面積の等しい円と正方形の描かれたウィトルウィウス的人体図。この作品がどう月と地球と結びつくのかというと、また別の「円の正方形化」が鍵になります。
先に説明したウィトルウィウス的人体図の円の正方形化は、面積が等しい円と正方形でした。
今度は周の長さが等しくなる円と正方形を描くと、月と地球との符合を見出せます。
人物が描かれている正方形(緑)に内接する円を地球とします。次に正方形と周の長さが同じ円(赤)を描く(円の正方形化:周)。正方形に内接する円(地球)と、正方形と同じ周の長さの円(赤)との間に生まれた隙間は月の半径に等しくなります。(精度:99.9%)

また、地球が内接する正方形と、月が内接する正方形を描けば3:4:5のピタゴラスの三角が導き出せます。

ウィトルウィウス的人体図は「面積の円の正方形化」をもとに人物が描かれていました。そして「周の円の正方形化」を求めることによって月と地球、ピタゴラスの三角形を見出すことができます。
少し作図の説明でややこしく感じたかも知れませんが、しっかり符合が見てとれましたね。
実はまだこの「円の正方形化」から繋がりを見出すことが出来るんです。
ではその繋がりをこちらの番人に導いてもらいましょう。

1:√3:2の正三角形もピタゴラスの定理が
ピラミッド
エジプトのスフィンクスに符合へと導いてもらいましたので、多くの謎を秘めている巨大建造物「ギザの大ピラミッド」について見ていきましょう。
ピラミッドは多くの幾何学的符合を示すのですが、今回は記事の内容にリンクするその一部を紹介します。
ピラミットの底面の半分を1とした時、高さは√Φ、ピラミッドの側面に沿う斜辺はΦになります。その直角三角形は「1:√Φ:Φ」、黄金比のピタゴラスの三角形です。

記事の前半で紹介した月と地球の直角三角形も「1:√Φ:Φ」の黄金比のピタゴラスの三角形。あの巨大な石の建造物からも、月と地球との符合が見出せます。

符合はそれだけではありません。先ほどウィトルウィウス的人体図の円の正方形化(周)によって、月と地球との符合を見出しましたが、ピラミッドもそれに当てはめることが出来ます。
正方形および内接する地球を二分割する中心線、そしてその線を月の中心点まで結ぶと、ピラミッドと同じ「1:√Φ:Φ」が収まる三角形を描くことができます。

また、ウィトルウィウス的人体図の円の正方形化(面積)とピラミッドを重ねると更に不思議な符合が見えてきます。
下の図はウィトルウィウス的人体図の円をピラミッドに内接させたものです。円と正方形を重ね合わせた人体図の中心位置はヘソになるのですが、ヘソから人物の手・正方形の角へ直線を伸ばすと、その位置はピラミッドの斜辺を黄金比で分割する位置になります。
つまり、ピラミッドに内接するように人体図を配置すると、人物が黄金比の分割ポイントを指さしているということです。(この画像を作っていてピッタリ黄金比の位置に手が重なった時は驚きました)

ここまで符合がたくさんあると感覚が麻痺してきそうですが、ウィトルウィウス的人体図もピラミッドも恐ろしいくらい計算されて作られたということが伺い知れます。そこにはどの時代・地域でも変わらない・変えようのない知恵が隠れていました。
その知恵の詰まった作品を残せるからこそ歴史に名を残す天才と呼ばれ、歴史に残る名作・遺産であるわけですね。
記事のボリューム的にはここまでの内容で締めに向かっても良いのですが、X(旧Twitter)でまだ紹介していない小ネタもあるので、簡単に紹介して記事の締めに向かいます。頭がパンクしそうでしたら軽い流し読みでも構いません。ご自分のペースで読んでいって下さいね。
それでは小ネタを見ていきましょう!
顔を覗かせる数字273
最後は数字「273」について見ていきます。藪から棒にこの数字を紹介するわけではないですよ!ちゃんとここまで書いてきた内容とリンクすることです。
周と面積、それぞれの円の正方形化について説明しましたが、ここからもう少し繋げましょう。
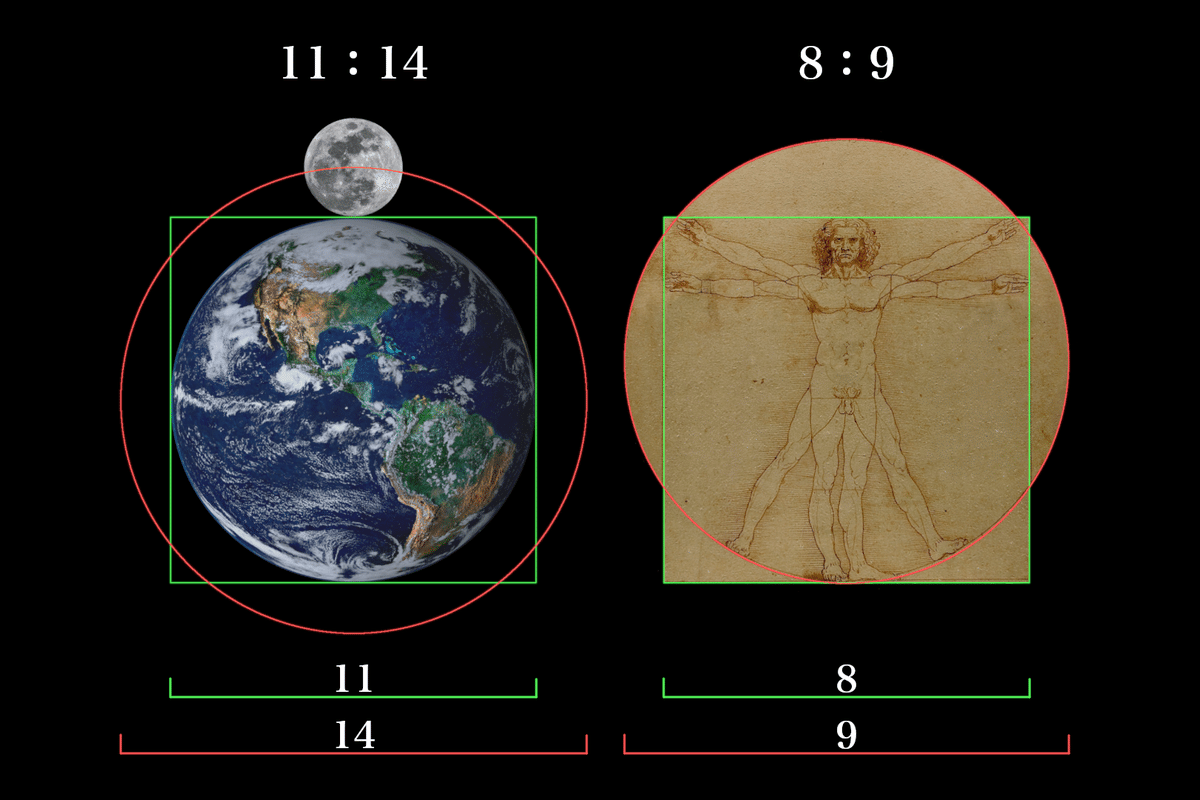
上の画像は、周・面積の円の正方形化の直径比を表したものです。それぞれの比は「11:14」「8:9」となっています。
「面積の円の正方形化」の直径比は8:9。8:9の比は音楽において長2度。また、1太陰年(354.4日)と木星の会合周期(398.9日)も8:9と、音楽・天文学との繋がりが見出せます。

そう言えば、ラグビーのコートサイズも8:9でした。しかもボールはヴェシカ・パイシス。

もう一方の「周の円の正方形化」ですが、その直径比は11:14。11:14の比を計算することによって273に繋がっていきます。
14÷11=1.273(小数点以下第四位切り上げ)
これだけではありません。円の正方形化により、円と正方形の周の長さは同じなので、正方形の直径を1とした時、円・正方形の周は4になります。そして円の直径を計算すると値は1.2732に(円周÷π)。

「周の円の正方形化」から273が顔を覗かせました。他にも色々と繋がるので箇条書きにしてまとめて見ました。
月と地球の比率3:11、パーセントにすると約27.3%
月の公転周期は27.3217日
月の脱出速度は2.378 km/s
絶対零度は-273.15℃
ケルビンでの水の凝固・融点は273.15K
夏至(6月21日)から春分(3月21日)までの日数は273日
閏年を足した1太陽年366日、これを割り算すると1÷366=0.00273…。反対に1を273で割ると1÷273=0.00366…
2732−2372=360 …鏡のように数字を引き算すると円の角度360
273は、この記事で見てきた円の正方形化(周)、月と地球との符合や、計算や暦においても顔を覗かせています。
と、最後におまけとして、今回の記事を書くにあたり数字について調べていたらこんなのを見つけました。

上の画像は「2012年12月3日にピラミッドの上空で2737年ぶりに水星・金星・土星が並んだ…」という写真です。実はこれデマです。嘘っぱちです。
この画像を見つけた時「こんなにはっきり同じ大きさで映るか?!」とビックリしたのですが、よくよく調べてみると加工写真であるとのこと。
この日の水星・金星・土星は日中の空にあり、写真のように夜撮影することは不可能だったそう。また、2737年という数字もデマであるとのことでした。
実はこの画像を使って情報発信している海外の有名ブロガーさんを見つけたので、一応皆さんへ注意喚起として紹介しました。(私は一瞬騙されましたw)
終わりに
以上で今回の記事は終わりなのですが、いかがだったでしょうか?何か新たな発見があったり、知識と知識が繋がる連鎖は起こりましたか?
前回の記事も合わせて書き終わり、振り返ってみると、久しぶりの数字や幾何学についての記事だったからか、ちょっと意気込み過ぎちゃったかな?と思いました。ですが、私なりになるべく噛み砕いて記事を書いたつもりです。
また、最後はファクトチェックについても紹介しましたが、記事の内容は私なりに計算したり調べたりして書き上げてあります。もし間違い等を発見しましたらXにてDMをくださると助かります。(質問もOKです!)
では今回の記事は終わりです。もし面白いと思って頂けましたらスキをお願いします!それでは次回の記事でまたお会いしましょう!

※無断での引用・転載禁止※
本記事を引用・転載されたい方はX(旧Twitter)にてメールして頂けましたら対応します。
noteプロフィールにあります、Xのアイコンからどうぞ。
