
<学習シリーズ>線形モデル編:ベイズ線形回帰
1.概要
1-1.緒言
本記事は”学習シリーズ”として自分の勉強備忘録用になります。
過去の記事で機械学習・AIの記事を多数作成しましたが、シンプルな線形モデルは外挿が比較的得意のためいろんな分野で使用されます。本記事では「ベイズ線形回帰」を学習します。
1-2.用語・記号の説明(全般)
本記事で使用する用語および記号は下記の通りです。
【用語一覧】
●回帰 (regression):実数値を予測する問題
●分類 (classification):カテゴリ(離散値)を予測する問題
●教師あり学習 (supervised learning):機械学習でデータセットに対して正解値(ラベル)がある学習方法
●教師なし学習 (unsupervised learning):機械学習でデータセットに対して正解値(ラベル)が無い学習方法
●予測値 (predicted value):関数で計算された出力変数y(用語は下記参照)
●目標値 (target value):予測値がとるべき値(教師あり学習の正解値)
●目的関数 (objective function):機械学習において性能の良さの指標を表す関数です。一般的には”予想値と目標値の差異”から作成される関数であり、この関数を最小化することでよいモデルと判断します。
●多重共線性(multicollinearity):多変量解析(重回帰分析など)において、いくつかの説明変数間で線形関係(強い相関関係)があると共線性といい、共線性が複数認められる場合は多重共線性があると言います。
●二乗和誤差 (sum-of-squares error):正解値$${y}$$と予測値$${\hat{y}}$$の差の2乗$${(y-\hat{y})^2}$$です。これをモデルと正解値の誤差とも呼びます。
●最小二乗法:二乗和誤差を最小化することでモデルの当てはまりを最適化する手法です。
【記号一覧】
●$${f()}$$:$${y=f(x)}$$におけるf()であり関数と呼びます。中身は入力変数xを処理して新しい出力変数yを生成する計算式です。
●$${x}$$:$${y=f(x)}$$におけるxです。複数は下記の通り複数あります。
名称1:説明変数(Explanatory variable)
名称2:独立変数(Independent variable)
名称3:外生変数(Exogenous variable)
名称4:入力変数(Input variable)
名称5:入力値(Input value)
●$${y}$$:$${y=f(x)}$$におけるyです。複数は下記の通り複数あります。
名称1:目的変数(Response variable)
名称2:従属変数(Dependent variable)
名称3:被説明変数(Explained variable)
名称4:内生変数(endogenous variable)
名称5:出力変数(Output variable)
名称6:予測値/推論値(prediction value)
●$${w_i}$$(weight):重み(単回帰の場合は傾きとも言う)
●$${b}$$(bias):バイアス(単回帰の場合は切片とも言う)
1-3.サンプル用データ
サンプルデータはScikit-learnのToy datasetsを使用します。今回は回帰(Regression)のため"diabetes"を使用しました。単回帰は変数が1つだけの1次元モデルのため、特徴量として重要な"s5"だけ抽出しました。
単回帰の理論値は傾き=1,021, 切片=173.1です。
[IN]
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import matplotlib.animation as animation
import japanize_matplotlib
import seaborn as sns
import os, glob, datetime, re, time, itertools, json
import requests
from bs4 import BeautifulSoup
from scipy.stats import norm
from tqdm import tqdm
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
#データセットの読み込み
diabetes = datasets.load_diabetes()
data, target = diabetes.data, diabetes.target
df_data = pd.DataFrame(data, columns=diabetes.feature_names)
df_data = df_data[['s5']] #単回帰として使用するため1次元のみ抽出
print(type(df_data), df_data.shape, type(target), target.shape)
#データの分割:参照用のデータ数を少なくする
x_train, x_test, y_train, y_test = train_test_split(df_data, target, test_size=0.98, random_state=0)
print(f'x_train: {x_train.shape}, x_test: {x_test.shape}, y_train: {y_train.shape}, y_test: {y_test.shape}')
#データの可視化
def plot_diabetes(xs, ys, title, verbose=False):
fig, ax = plt.subplots(1, 1, figsize=(8, 5), facecolor='w')
ax.scatter(xs, ys, color='blue', label='train')
if verbose:
for x, y in zip(xs.values, ys):
ax.text(x, y, f'(x:{float(x):.4f}, y:{int(y):d})', fontsize=10)
ax.set(xlabel='s5', ylabel='target')
ax.set_title(title, y=-0.2)
plt.grid()
plt.show()
plot_diabetes(x_train, y_train, 'Fig. Diabetesデータにおけるs5と1年後の糖尿病進行度の関係', verbose=True)
#単回帰で正解値を予測する
x = np.array([0.01482, 0.00784, 0.08450, 0.12902, -0.02953, 0.07912, -0.01812, 0.07341])
y = np.array([311, 122, 243, 248, 91, 281, 142, 295])
linear = LinearRegression()
linear.fit(x.reshape(-1, 1), y)
print(f"alpha(傾き): {linear.coef_[0]:.3f}, beta(切片): {linear.intercept_:.3f}")[OUT]
<class 'pandas.core.frame.DataFrame'> (442, 1) <class 'numpy.ndarray'> (442,)
x_train: (8, 1), x_test: (434, 1), y_train: (8,), y_test: (434,)
alpha(傾き): 1020.808, beta(切片): 173.105
2.単回帰(線形モデル)とは:y=ax+b
単回帰分析とは 1 つの入力変数$${x}$$から 1 つの出力変数$${y}$$を推測する処理です。入力値に重みをかけバイアスを足したものを回帰方程式、グラフを回帰直線と呼びます。モデルの形が直線になることから線形モデルとも呼ばれます。
$$
単回帰:y = ax+b
$$
●$${x}$$:入力変数
●$${y}$$(または$${\hat y}$$):出力変数
●$${a}$$:傾き(機械学習では重みと呼び$${w}$$を使う)
●$${b}$$:切片(またはバイアス)
推定値$${\hat y}$$とデータ値$${y_i}$$の誤差を最小にすることで最適なパラメータ$${a}$$, $${b}$$を決定できます。
3.線形ベイズの理解
線形ベイズの概念的な部分を定性的に説明します。
3-1.データの分布に関して
統計学の記事で説明した通りデータには分布がある、つまりばらつきがあります。実験データやサンプリング結果も同じであり、真の母集団は確認できないため得られる結果は標本であり必ず分布が生じます。
例としてある実験(反応活性試験を想定)で条件3点測定した結果が$${(x_1, y_1) = (1, 2)}$$, $${(x_2, y_2) = (2, 4)}$$, $${(x_3, y_3) = (3, 6)}$$とします。これを単回帰で推論するなら$${y=2x}$$となります。

しかし、実験データは様々な要因(充填量、分析器誤差など)で結果がばらつきます。よって同じ条件でも複数回測定すれば別の結果が得られます。その結果から単回帰$${y=2x}$$、つまりパラメータ$${w=2}$$は前と異なる値となります。つまり「今あるデータに完全にフィッティングさせるのはばらつきを考慮していない。よって、パラメータwの分布をとることでばらつきを考慮すべき」ということが分かります。

つまり最初の事例では「傾き$${w=2}$$は100%の確率」としていたのですが、データの分布を考慮すると「傾き$${w=2}$$が尤もらしいけど$${-1<w<5}$$くらいにはなりそう」という(確率)分布で表し、推論時はこの分布から確率的にパラメータをサンプリングすることでデータのばらつきを表すことが出来ることが分かります。
下図はパラメータの確率分布のイメージです。分散が小さい、つまりデータのばらつきが小さいと確率分布がシャープになるため、パラメータをより強い自身で選択していることが分かります。逆にばらつきが大きいとどれが正しいパラメータかわからないため幅広い値をとります。

ベイズ線形ではパラメータの事後分布を取得することで確率的(ばらつきを考慮した)な推論が可能となります。なお事後分布が複雑な形状になるとサンプリングが難しくなるためMCMCという手法が使われます。
4.理論:共役事前分布でのベイズ線形回帰
4-1.結論
最終的に求める事後分布(多変量ガウス分布)の平均ベクトルと分散共分散行列は下記になります。
$$
\mu_{\text{post}} = \Sigma_{\text{post}} (\beta X^T y)
$$
$$
\Sigma_{\text{post}} = (\alpha I + \beta X^T X)^{-1}
$$
4-2.基礎用語・単語・数式の説明
基礎的な内容は下記の通りです。詳細は別記事に記載しています。
事前分布(Prior): データを見る前のパラメータ(この場合はモデルの重み w)の確率分布。通常初めてデータを観察する前はパラメータについて何も知らないため、等確率な分布(一様分布)や中心0のガウス分布(正規分布)などを事前分布とすることが多いです。本ケースでは平均が0で精度が$${\alpha}$$の正規分布を事前分布とします($${I}$$は単位行列)。
$${\alpha}$$は事前分布の精度であり分散の逆数となります。よって${\alpha}$$が大きいほど事前分布は原点(0)に対してシャープ(つまり、狭い)になり、${\alpha}$$が小さいほど事前分布は原点に対してフラット(つまり、広い)になります。したがって、${\alpha}$$は私たちが事前にパラメータについて持っている信念の強さを制御します。${\alpha}$$が大きければ大きいほど、私たちはパラメータが特定の値であると強く信じている(分散が小さい)と解釈できます。
$$
事前分布:P(w) = \mathcal{N}(w | 0, \alpha^{-1}I)
$$
尤度(Likelihood): パラメータ w が与えられたときに、観測データ(正解値) y がどの程度尤もらしいか(どの程度観測されやすいか)を表す確率分布。尤度はパラメータが与えられたときのデータの確率分布で、通常、この分布は観測データに依存します。
線形回帰では、観測データ(正解値) y は入力 x とパラメータ w の線形結合にガウスノイズが加わったものと仮定されます。$${\beta}$$は尤度のスケールであり逆数は観測ノイズの分散を表します。性質は${\alpha}$$と同じです。
Xはデザイン行列で各行が観測データの特徴ベクトルを表し、1列目にバイアス項$${w_0}$$用のベクトルを持ちます。。
$$
尤度: P(y | X, w) = \mathcal{N}(y | Xw, \beta^{-1})
$$
$$
X = \begin{bmatrix} 1 & x_{1,1} & x_{1,2} & \cdots & x_{1,d} \\
1 & x_{2,1} & x_{2,2} & \cdots & x_{2,d} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & x_{n,1} & x_{n,2} & \cdots & x_{n,d} \end{bmatrix},
w = \begin{bmatrix} w_{0} \\ w_{1} \\ w_{2} \\ \vdots \\ w_{d} \end{bmatrix}
$$
事後分布(Posterior): データを観測した後の、パラメータ w の確率分布。事後分布はベイズの定理により、事前分布と尤度から計算されます。
$$
事後分布: P(w | X, y) \propto P(y | X, w)P(w)
$$
ベイズ線形回帰では、事前分布と尤度が共にガウス分布であるときに事後分布はガウス分布になり、この時の事前分布は共役事前分布と呼ばれます。この事後分布の平均ベクトルと共分散行列は以下のように計算されます。
$$
事後分布の平均: \mu_{\text{post}} = \beta \Sigma_{\text{post}} X^T y
$$
$$
事後分布の共分散行列: \Sigma_{\text{post}} = (\alpha I + \beta X^T X)^{-1}
$$
4-3.式の導出
事前分布と尤度を下記とするとベイズの定理より事後分布は$${P(w | X, y) \propto P(y | X, w) P(w)}$$となります。
$$
事前分布:P(w) = \mathcal{N}(w | 0, \alpha^{-1}I)
= \frac{1}{\sqrt{(2\pi)^d|\alpha^{-1}I|}} \exp\left(-\frac{1}{2} w^T (\alpha I) w \right)
$$
$$
P(y | X, w) = \mathcal{N}(y | Xw, \beta^{-1}I) = \frac{1}{\sqrt{(2\pi)^n|\beta^{-1}I|}} \exp\left(-\frac{1}{2} (y - Xw)^T (\beta I) (y - Xw) \right)
$$
対数を取ると事後分布の対数は尤度の対数と事前分布の対数の和になり、これらを具体的に書くと次のようになります。
$$
\begin{aligned}
\ln P(w | X, y) & \propto -\frac{1}{2} w^T (\alpha I) w -\frac{1}{2} (y - Xw)^T (\beta I) (y - Xw) + \text{const.} \\
& \propto -\frac{1}{2} w^T (\alpha I + \beta X^T X) w + w^T (\beta X^T y) + \text{const.}
\end{aligned}
$$
求めた対数式は平均が $${\mu_{\text{post}} }$$、共分散行列が $${\Sigma_{\text{post}} }$$ のガウス分布の対数と一致します。すなわち下記となります。
$$
事後分布の平均: \mu_{\text{post}} =\Sigma_{\text{post}} (\beta X^T y)
$$
$$
事後分布の共分散行列: \Sigma_{\text{post}} = (\alpha I + \beta X^T X)^{-1}
$$
4-4.ポイント:データの正規化
正規化とはデータを平均0, 標準偏差1へ変換する処理であり計算式は下記の通りです。本処理では事前に正規化しないとうまくいきませんでした。おそらく特徴量・ラベル間のスケール差が影響するのかもしれませんが証明は難しかったので省略します。
$$
正規化:x_{std} = \frac{データ-平均値}{標準偏差}= \frac{x-\mu_x}{\sigma}
$$
単回帰モデルは傾き$${w_1}$$、切片$${w_0}$$遠くと下記の通りです。
$$
\begin{aligned}
単回帰モデル:y = w_0 + w_1 x
\end{aligned}
$$
説明変数$${x}$$、目的変数$${y}$$を正規化すると下記の通りです。
$$
\begin{aligned}
x' = \frac{x - X_{\text{mean}}}{X_{\text{std}}} ,
y' = \frac{y - y_{\text{mean}}}{y_{\text{std}}}
\end{aligned}
$$
正規化したデータに対する線形回帰モデルは下記の通りです。この時のパラメータ$${w_0, w_1}$$は正規化されたデータに対する値となります。
$$
\begin{aligned}
y' = w_0' + w_1' x'
\end{aligned}
$$
正規化された推論値$${y'}$$のスケールを元に戻すと
$$
\begin{aligned}
y &= y_{\text{std}} * y' + y_{\text{mean}} \\
&= y_{\text{std}} * (w_0' + w_1' * x') + y_{\text{mean}} \\
&= y_{\text{std}} * w_0' + y_{\text{std}} * w_1' * \frac{x - X_{\text{mean}}}{X_{\text{std}}} + y_{\text{mean}} \\
&=( y_{\text{std}}* w_0' + y_{\text{mean}} -y_{\text{std}} * w_1' * X_{\text{mean}} / X_{\text{std}}) + (y_{\text{std}}* w_1' /X_{\text{std}}) x
\end{aligned}
$$
正規化でフィッティングされたパラメータを元に戻すと
$$
\begin{aligned}
&切片:w_0 = y_{\text{std}} * w_0' + y_{\text{mean}} - y_{\text{std}} * \frac{w_1' * X_{\text{mean}}}{X_{\text{std}}} \\
&傾き:w_1 = \frac{y_{\text{std}} * w_1'}{X_{\text{std}}}
\end{aligned}
$$
5.単回帰モデルの実装:スクラッチ編
動作を理解するためにPythonのライブラリを使用せずスクラッチで計算します。目視で確認できるようにデータ数を1桁に調整しました。
再掲載ですが単回帰の理論値は傾き=1,021, 切片=173.1です。

5-1.Excelで計算
下記手順で計算しました。結果として特定の分散を持つ正規分布として傾き=907.4, 切片=214.6となりました。
理論値から数値がずれるのは事前分布として標準正規分布(平均0, 分散1)を使用しており、この影響で事後分布がシフトしたと思います。
正規化のため説明変数$${X}$$と目的変数$${y}$$の平均値・分散を求める
求めた平均値・分散からデータを正規化
事後分布の精度行列$${(\alpha I + \beta X^T X)}$$を算出
精度行列の逆数を取り事後分布の共分散行列$${\Sigma_{\text{post}}=(\alpha I + \beta X^T X)^{-1}}$$を算出
求めた値から平均ベクトル$${\mu_{\text{post}} = \Sigma_{\text{post}} (\beta X^T y)}$$を算出
正規化向けの平均ベクトルを元に戻す。

5-2.Pythonで計算
PythonでもExcelと同様に計算しますが、より詳細に可視化しました。
5-2-1.実装
実装はクラスにまとめて下記実行しました。
【fit関数】
正規化のため説明変数$${X}$$と目的変数$${y}$$の平均値・分散を求める
求めた平均値・分散からデータを正規化
事後分布の精度行列$${(\alpha I + \beta X^T X)}$$を算出
精度行列の逆数を取り事後分布の共分散行列$${\Sigma_{\text{post}}=(\alpha I + \beta X^T X)^{-1}}$$を算出
求めた値から平均ベクトル$${\mu_{\text{post}} = \Sigma_{\text{post}} (\beta X^T y)}$$を算出
正規化向けの平均ベクトルを元に戻す。
【predict関数】
fit関数で得られた事後分布の平均ベクトルと分散共分散行列から事後分布として多変量ガウス分布を計算し、その事後分布からサンプリングする(np.random.multivariate_normal())
サンプリングしたデータ(つまり切片と傾き)から単回帰$${y = w_0 + w_1 * x}$$で推論値を計算する
上記は正規化された値のため元の数値に戻す$${y= y_{mean} + y_{pred}y_{\text{std}}}$$
【plot_prediction関数】
結果の可視化用
[IN]
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
class BayesianLinearRegression:
def __init__(self, alpha: float = 1.0, beta: float = 1.0):
self.alpha = alpha # 事前分布の精度パラメータ
self.beta = beta # 事前分布の平均パラメータ
self.w_mean = np.zeros(2) # 正規分布の平均
self.w_precision = np.zeros((2, 2)) # 正規分布の精度行列(分散共分散行列Σの逆行列Σ^-1)
def fit(self, X, y, visualize = False):
# データの正規化
self.X_mean, self.X_std = X.mean(), X.std() # 平均と標準偏差を保存
self.y_mean, self.y_std = y.mean(), y.std() # 平均と標準偏差を保存
X = (X - self.X_mean) / self.X_std #Xの正規化
y = (y - self.y_mean) / self.y_std #yの正規化
# データ行列を作成
X_design = np.vstack((np.ones(len(X)), X)).T # データ行列Xの1列目に1を追加(バイアス項),2列はX
# 事後分布の平均と精度行列を計算
self.w_precision = self.alpha * np.eye(2) + self.beta * X_design.T @ X_design # 精度行列:Σ^-1 = αI + βX^TX(分散共分散行列Σの逆行列Σ^-1)
self.w_mean = self.beta * np.linalg.inv(self.w_precision) @ (X_design.T @ y) #平均ベクトル:傾きと切片の推定値
# for i in range(len(X)):
# x_i = X_design[i:i+1] # i番目のデータX(説明変数)
# y_i = y[i:i+1] # i番目のデータy(目的変数)
# # 事後分布の平均と精度行列を計算
# self.w_precision = self.alpha * np.eye(2) + self.beta * x_i.T @ x_i # 精度行列:Σ^-1 = αI + βX^TX(分散共分散行列Σの逆行列Σ^-1)
# self.w_mean = self.beta * np.linalg.inv(self.w_precision) @ (x_i.T @ y_i) #平均ベクトル:傾きと切片の推定値
# 事前分布と事後分布を描画
# if visualize:
# self.plot_distribution(x_i, y_i, i+1, save=True)
# 正規化されたパラメータを保存
self.normalized_w_mean = self.w_mean.copy()
# 正規化されたパラメータを元のスケールに戻す
self.w_mean[0] = self.w_mean[0]*self.y_std + self.y_mean - self.w_mean[1]*self.X_mean*self.y_std #w0 = w0*σy + μy - w1*μx*σy
self.w_mean[1] = self.w_mean[1]*self.y_std/self.X_std #w1 = w1*σy/σx
def predict(self, X, sample_size: int = 5):
# データの正規化
X = (X - self.X_mean) / self.X_std
# データ行列を作成
X_design = np.vstack((np.ones(len(X)), X)).T # データ行列Xの1列目に1を追加(バイアス項),2列はX
# 事後分布(2変量正規分布)からパラメータをサンプリング
w_samples = np.random.multivariate_normal(self.normalized_w_mean, # 平均ベクトル
np.linalg.inv(self.w_precision), #分散共分散行列Σ
size=sample_size) # サンプル数
# 予測
y_preds = X_design @ w_samples.T
# スケールを元に戻す
y_preds = y_preds * self.y_std + self.y_mean
return y_preds, w_samples
def plot_distribution(self, x, y, num_iter:str, save=False):
prior_distribution = multivariate_normal(self.w_mean, np.linalg.inv(self.w_precision))
posterior_distribution = multivariate_normal(self.w_mean, np.linalg.inv(self.w_precision + self.beta * x.T @ x))
# パラメータ空間の描画
w0, w1 = np.mgrid[-1:1:.01, -1:1:.01]
pos = np.empty(w0.shape + (2,))
pos[:, :, 0] = w0; pos[:, :, 1] = w1
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
ax1.contourf(w0, w1, prior_distribution.pdf(pos))
ax2.contourf(w0, w1, posterior_distribution.pdf(pos))
ax1.set(title=f'事前分布:{num_iter}回目', xlabel='w0(切片)', ylabel='w1(傾き)')
ax2.set(title=f'事後分布:{num_iter}回目', xlabel='w0(切片)', ylabel='w1(傾き)')
ax1.grid(); ax2.grid()
if save:
fig.savefig(f'temp/fig{num_iter}.png')
plt.show()
def plot_prediction(self, X, y, sample_size: int = 5):
y_preds, w_samples = self.predict(X, sample_size)
#パラメータの正規化を戻す
w_samples[:, 0] = w_samples[:, 0]*self.y_std + self.y_mean - w_samples[:, 1]*self.X_mean*self.y_std #w0 = w0*σy + μy - w1*μx*σy
w_samples[:, 1] = w_samples[:, 1]*self.y_std/self.X_std #w1 = w1*σy/σx
# 予測結果をプロット
color_list = ['red', 'orange', 'black', 'blue', 'purple']
plt.figure(figsize=(10, 5))
plt.scatter(X, y, color='blue', label='Actual')
plt.plot(X, self.w_mean[0] + self.w_mean[1]*X, color='green', label=f'MAP:y={self.w_mean[1]:.1f}x+{self.w_mean[0]:.1f}')
for i, (w0, w1) in enumerate(w_samples):
plt.plot(X, y_preds[:, i], color=color_list[i], alpha=0.6, label=f'y={w1:.1f}x+{w0:.1f}')
plt.legend(), plt.grid()
plt.show()
X = np.array([0.01482, 0.00784, 0.08450, 0.12902, -0.02953, 0.07912, -0.01812, 0.07341])
y = np.array([311, 122, 243, 248, 91, 281, 142, 295])
model = BayesianLinearRegression()
model.fit(X, y, visualize=False)
model.plot_prediction(X, y)
print(model.w_mean)
[OUT]
[214.57909894 907.38484604]
事後分布からパラメータとして切片と傾きをサンプリングしているため何本も線が描けていることが確認できます。つまり、1個のパラメータ(切片、傾き)を言い切るのではなく、得られた分布から確率的にモデルのパラメータを選定していることが確認できます。
5-2-2.事後分布の可視化
事後分布=事前分布×尤度であり、得られたデータに応じたパラメータ(正規化前)の尤もらしさの分布です。これを3Dプロットと等高線図の2パターンで可視化しました。
結果としてパラメータである切片と傾きは確率密度を持つ事後分布として表され、この事後分布からサンプリングすることでパラメータを一意に定めることなく、他の可能性(ばらつきを考慮した)も含めたグラフを作成することが出来ます。
[IN]
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
w0, w1 = model.normalized_w_mean
matrix_var_cov = np.linalg.inv(model.w_precision)
x1 = np.linspace(-2, 2, 100)
x2 = np.linspace(-2, 2, 100)
x1, x2 = np.meshgrid(x1, x2)
#3次元プロット
Z = multivariate_normal.pdf(np.dstack((x1, x2)), mean=[w0, w1], cov=matrix_var_cov)
# 3Dプロットを作成
fig = plt.figure(figsize=(12, 6))
# 3Dプロット
ax1 = fig.add_subplot(121, projection='3d')
ax1.plot_surface(x1, x2, Z, rstride=3, cstride=3, linewidth=1, antialiased=True, cmap=cm.viridis)
# タイトルとラベル
ax1.set_title("3Dプロット")
ax1.set_xlabel('切片:w0')
ax1.set_ylabel('傾き:w1')
# 等高線図を作成
ax2 = fig.add_subplot(122)
ax2.contourf(x1, x2, Z)
# タイトルとラベル
ax2.set_title("等高線図")
ax2.set_xlabel('切片:w0')
ax2.set_ylabel('傾き:w1')
# プロットを表示
plt.show()
[OUT]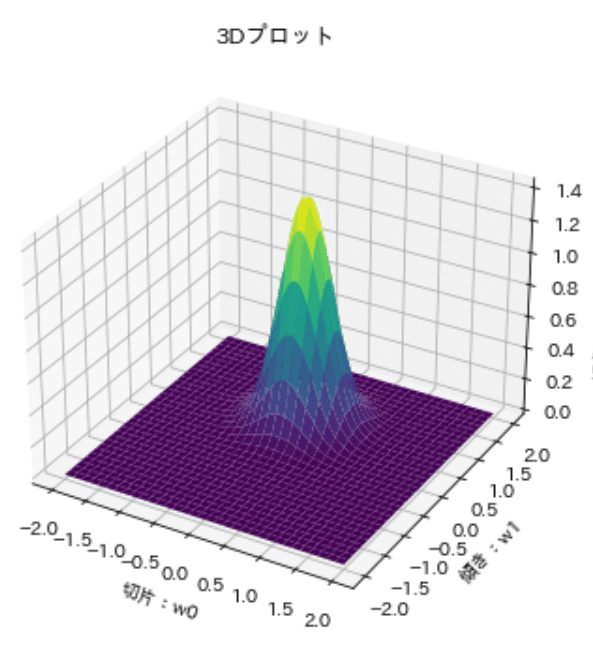

6.理論:複雑な事後分布×MCMCによるベイズ線形回帰
前章では事前分布に共役事前分布を使用することで事後分布も特定の確率分布であることを保証することで、事後分布から簡単にサンプリングできました。しかし事前分布が共役事前分布でないと事後分布が一般的な確率分布でなくなるため簡単にサンプリングできなくなります。
得られた事後分布を確率分布としてサンプリングする手法にマルコフ連鎖モンテカルロ法(Markov chain Monte Carlo methods:MCMC)があります。
本章ではMCMCを使用して同様に事後分布からパラメータをサンプリングして単回帰の不確実性を表現します。
6-1.実装
追って
[IN][OUT]6-2.コラム:数式とコードの動作確認
数式と動作に関して簡単に紹介します。
【尤度関数(likelyhood)】
線形回帰モデルを考える場合、各観測値は$${y_i}$$は独立に次のように分布しているとします。
$$
y_i= \mathcal{N}(ax_i+b, \sigma^2)
$$
観測データを固定すると尤度(パラメータの尤もらしさ)はパラメータの関数となります
$$
L(a, b | \mathbf{y}, \mathbf{x}) = \prod_{i=1}^N \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(y_i - ax_i - b)^2}{2\sigma^2}\right)
$$
さらに計算を楽にするために対数を取ります。
$$
\log L(a, b | \mathbf{y}, \mathbf{x}) = -\frac{N}{2}\log(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^N (y_i - ax_i - b)^2
$$
7.単回帰モデルの実装:ライブラリ編
より簡単にモデルを作成するためにライブラリを使用します。
7-1.PyMC3
PyMC3を使用して事前分布と尤度からMCMCにより事後分布を求めて、パラメータの不確実性を表現します。事前分布は理論値と比較できるように一様分布(無情報事前分布:pm.Flat())を使用しました。
またプロット用にMAP推定値も合わせて取得しました。
$$
P(\theta | D) = \frac{P(D | \theta) P(\theta)}{P(D)}
$$
[IN]
import pymc3 as pm
import arviz as az
X = np.array([0.01482, 0.00784, 0.08450, 0.12902, -0.02953, 0.07912, -0.01812, 0.07341])
y = np.array([311, 122, 243, 248, 91, 281, 142, 295])
with pm.Model() as model:
# 事前分布
intercept = pm.Flat('intercept') # 切片
slope = pm.Flat('slope') # 係数
sigma = pm.HalfNormal('sigma', sd=1) # 予測の誤差
# モデル
mu = intercept + slope * X
# 尤度
likelihood = pm.Normal('likelihood', mu=mu, sd=sigma, observed=y)
# 事後分布のサンプリング
trace = pm.sample(1000, chains=2, random_seed=0)
#MAP推定値を取得
MAP_estimate = pm.find_MAP()
#事後分布の要約
summary = pm.summary(trace) # 事後分布の要約統計量
display(summary)
#MAP推定値
print(MAP_estimate)
# 事後分布の可視化
with model:
pm.plot_trace(trace) # トレースプロット
pm.plot_posterior(trace) # 事後分布の分布
[OUT]
{'intercept': array(173.10533446),
'slope': array(1020.809589),
'sigma_log__': array(2.54675874),
'sigma': array(12.76565978)}
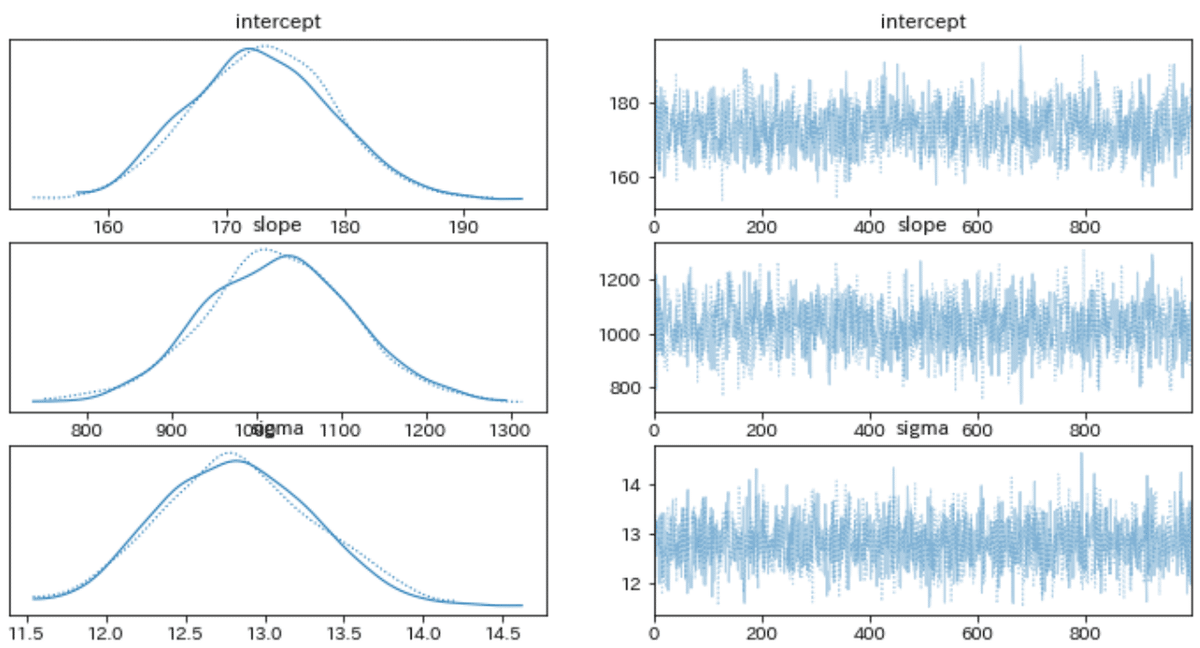

事後分布からのサンプリングデータは"trace"に格納されています。よって、この中からデータをサンプリングすることで複数のパラメータによる結果を得られ、不確実性を表現できます。
[IN]
samples_intercept = trace['intercept']
samples_slope = trace['slope']
plt.plot(samples_intercept, label='事後分布からサンプリングした切片')
plt.plot(samples_slope, label='事後分布からサンプリングした傾き')
plt.legend()
[OUT]
最後に1.単回帰(最小二乗法による決定的なパラメータ)、2.MAP推定(事後分布の最大値)、3.事後分布のサンプリング値(パラメータの不確実性を考慮) をプロットしました。なお事後分布はトレースプロットを確認したうえで、(最初から安定しているように見えますが念のため)バーンインの影響を除くためにデータの半分をサンプリングから削除しました
[IN]
#プロット用データ
x_plot = np.linspace(-0.05, 0.15, 100)
#生データ
fig, ax = plt.subplots(1, 1, figsize=(8, 5), facecolor='w')
ax.scatter(X, y, color='blue', label='生データ')
ax.set(xlabel='RM', ylabel='target')
#線形回帰モデル
linear = LinearRegression()
linear.fit(X.reshape(-1, 1), y)
intercept_linear, slope_linear = linear.intercept_, linear.coef_
y_pred_linear = intercept_linear + slope_linear * x_plot
ax.plot(x_plot, y_pred_linear, color='blue', label=f'単回帰:y={slope_linear[0]:.1f}x+{intercept_linear:.1f}')
#MAP推定値を用いた予測
slope_MAP = MAP_estimate['slope']
intercept_MAP = MAP_estimate['intercept']
y_pred_MAP = intercept_MAP + slope_MAP * x_plot
ax.plot(x_plot, y_pred_MAP, color='red', label=f'MAP:y={slope_MAP:.1f}x+{intercept_MAP:.1f}', ls='--')
#事後分布からのサンプリングによる予測
burnin = 500 # 最初の500サンプルを捨てる
num_samples = 5 # サンプル数
for i in range(num_samples):
# 事後分布からサンプリング
slope_sample = trace['slope'][burnin+i]
intercept_sample = trace['intercept'][burnin+i]
# 予測値を計算
y_pred_sample = intercept_sample + slope_sample * x_plot
# 予測値をプロット
plt.plot(x_plot, y_pred_sample, alpha=0.3, label=f'sample:y={slope_sample:.1f}x+{intercept_sample:.1f}')
ax.legend(), ax.grid()
plt.show()
[OUT]
今回は一様分布を使用したため単回帰とMAP推定値は同じ値となっております。また事後分布からサンプリングすることでパラメータ(ここでは傾きと切片)を一意に決めることなく幅を持って表現できていることが確認できました。
【コラム:事前分布の設定による失敗例】
事前分布に一様分布でなく標準正規分布を使用した場合は下記の通りとなります。事後分布は当然事前分布の影響を受けるのですが、尤度で補正されるため最終的には期待される値に近づくと思っていたのですが、全く異なる値となりました。
おそらくですが事前分布が事後分布のパラメータに大きな影響を与えたと思うのですが簡単に証明できなかったたため分かり次第追記します。
とりあえずパラメータに自信がなければ一様分布、自信があれば事前分布を使った方がよさそうな気はします。
[IN]
with pm.Model() as model:
# 事前分布
intercept = pm.Normal('intercept', mu=0, sd=1) # 切片
slope = pm.Normal('slope', mu=0, sd=1) # 係数
sigma = pm.HalfNormal('sigma', sd=1) # 予測の誤差
# モデル
mu = intercept + slope * X
# 尤度
likelihood = pm.Normal('likelihood', mu=mu, sd=sigma, observed=y)
# 事後分布のサンプリング
trace = pm.sample(1000, chains=2, random_seed=0)
#MAP推定値を取得
MAP_estimate = pm.find_MAP()
#事後分布の要約
summary = pm.summary(trace) # 事後分布の要約統計量
display(summary)
#MAP推定値
print(MAP_estimate)
# 事後分布の可視化
with model:
pm.plot_trace(trace) # トレースプロット
pm.plot_posterior(trace) # 事後分布の分布
[OUT]
{'intercept': array(2.66585059),
'slope': array(0.14881694),
'sigma_log__': array(3.23234112),
'sigma': array(25.33890901)}


参考資料
資料1.線形モデルシリーズ
資料2.Pythonライブラリ
資料3.計算処理
資料4.ベイズ線形関係
あとがき
MCMCのハミルトニアンモンテカルロ法を理解出来たら、後はガウス過程(Gaussian Process)に入れるはず。
この記事が気に入ったらサポートをしてみませんか?
