
<学習シリーズ>Pytorchで線形モデル作成+学習動作を学んでみた
1.概要
本記事は”学習シリーズ”として自分の勉強備忘録用になります。
過去にディープラーニング(深層学習)における全結合を勉強するために(順伝搬・逆伝搬)の記事を作成しました。今回は復習もかねてPytorchで線形モデルを作成しながら動作確認と深層学習(主に逆伝搬)を勉強します。
基本的にPytorchの操作は細かく説明しないため動かし方は下記記事をご参考ください。
2.計算モデル式(y=wx+b)の確認
今回使用するモデルは動作が分かりやすいようにするために最もシンプルな関数である線形式$${y=wx+b}$$を使用しました。
2-1.記号の説明
各記号の意味は下記の通りです。
$$
y_{c}またはy_{label}:正解データ(目的値
$$
$$
x:入力値(説明変数)
$$
$$
w:重み(線形式の場合は傾き)
$$
$$
b:バイアス(線形式の場合は切片)
$$
$$
lr(η):学習率(勾配を更新する時の係数)
$$
2-2.線形モデルの計算グラフ
後ほど両方のグラフは使用しますが、各計算グラフでの"$${y=wx+b}$$"の部分は下図赤枠の通りです。


3.学習用データの作成
学習データとしてxは適当な連番、yは傾き=5でランダムに値がずれるように乱数を加えました。なお再現性がとれるように"torch.manual_seed(0)"で乱数シードを固定しています。また後で使うライブラリをインポートします。
[IN]
import torch
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
from torchviz import make_dot
torch.manual_seed(0) #乱数のシードを設定
x = torch.arange(-2, 2.1, 0.25)
y_label = 5*x + torch.randn(len(x))
print(x, y_label)
#Matplotlibでグラフを描画
plt.scatter(x, y_label, label='正解値')
plt.legend()
plt.grid()
[OUT]
tensor([-2.0000, -1.7500, -1.5000, -1.2500, -1.0000, -0.7500, -0.5000, -0.2500,
0.0000, 0.2500, 0.5000, 0.7500, 1.0000, 1.2500, 1.5000, 1.7500,
2.0000])
tensor([-11.1258, -10.4459, -6.9333, -5.4565, -4.4012, -5.3051, -2.8414,
0.6030, 0.4681, 0.6645, 2.3266, 3.9335, 6.3894, 7.8363,
8.4463, 7.9063, 10.9318])
次章以降で適当な重みwを逆伝搬で最適化していきますが、事前にsklearnで回答を確認しており「w=5.34, b=0.18」を目指すようにします。
[IN]
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x.reshape(-1, 1), y_label)
print(f'重みw:{model.coef_[0]:.2f}, バイアスb:{model.intercept_:.2f}')
[OUT]
重みw:5.34, バイアスb:0.184.Pytorchによる実装と勾配(grad)の理解
4-1.パラメーターおよびモデル作成
線形モデル$${y=wx+b}$$を作成します。パラメータは適当に$${w}$$には乱数値、$${b}$$には1.0の値を初期値として、予測関数pred(x)を作成します。
逆伝搬できるようにパラメータには"require_grad=True"を設定します。
(※前章の通り入力値xにはgradは不要)
[IN]
#パラメーターの設定
w = torch.randn(1, requires_grad=True) #重みを設定:ランダム値Ver.
b = torch.tensor(1.0, requires_grad=True) #バイアスを設定:固定値Ver.
print('重みw情報:', w, w.shape)
print('バイアスb情報:' ,b, b.shape)
def pred(x): #予測値を計算する関数
return w*x + b
[OUT]
重みw情報: tensor([0.4154], requires_grad=True) torch.Size([1])
バイアスb情報: tensor(1., requires_grad=True) torch.Size([])4-2.目的関数(損失関数)の設定:MSE
モデルによる予想値(y_pred)と目標値(y_label)の差を小さくするためにパラメータ(w, b)を変更していきますが、その差を求めるための関数を損失関数と言います。
今回の目的関数は回帰分析で一般的に使用される平均二乗誤差(MSE: Mean Square Error)を使用しました。
$$
MSE= \frac{1}{n}\sum_{i=1}^{n}(y_{pred}-y_{label})^2
$$
[IN]
def mean_squared_error(y_pred, y_label): #損失関数を計算する関数
return ((y_pred - y_label)**2).mean()
[OUT]
特になし4-3.残差(loss)および勾配(grad)の計算
計算手順は下記の通りです。
予測モデルで推定値(y_pred)を計算する
損失関数(mean_squared_error)で"誤差の平均:loss"を計算する
loss.backward()で逆伝搬を実施して勾配を求める
結果から下記のことが確認できた。
xはrequires_grad=Falseでy, w, bはTrueである
損失関数から得られたloss(torch型)の"backward()メソッド"を実行すると自動で勾配が計算される。
loss.backward()後にwとbそれぞれに勾配データが取得できた。
[IN]
y_pred = pred(x) #予測値を計算
print('勾配情報の確認', 'x:', x.requires_grad, 'y_pred:', y_pred.requires_grad, 'w:', w.requires_grad, 'b:', b.requires_grad, end='\n\n')
loss = mean_squared_error(y_pred, y_label) #平均二乗誤差を計算
print('loss:', loss)
print(type(loss), loss.shape, loss.dtype, end='\n\n')
print('loss.backward()前', 'w.grad:', w.grad, 'b.grad:', b.grad)
loss.backward() #勾配を計算
print('loss.backward()後', 'w.grad:', w.grad, 'b.grad:', b.grad)
[OUT]
勾配情報の確認 x: False y_pred: True w: True b: True
loss: tensor(38.0037, grad_fn=<MeanBackward0>)
<class 'torch.Tensor'> torch.Size([]) torch.float32
loss.backward()前 w.grad: None b.grad: None
loss.backward()後 w.grad: tensor([-14.7817]) b.grad: tensor(1.6475)5.★自動計算の仕組みを理解(逆伝搬)★
"loss.backward()"をすると自動でw=tensor([-14.7817]) , b=tensor(1.6475)の値が得られたがこの仕組みを理解していく。
5-1.計算グラフの確認:make_dot
計算グラフの出力は”make_dot()”を使用します。出力結果より下記が確認できます。詳細は次節で説明しますが逆伝搬が使える条件がそろっていることが分かります。
上部赤枠が$${y=wx+b}$$, 下青枠がMSEを示していることが確認できる。
"loss"の計算で使用したすべての変数が計算グラフで表現されている。
[IN]
g = make_dot(loss, params={'w':w, 'b':b})
display(g)
[OUT]
5-2.連鎖律(チェインルール)
本記事ではPytorchの動作検証がメインとなるため細かい逆伝搬の説明は下記記事をご確認ください。
(今回における)チェインルールとは下記のような拡張は数式的に成り立つことと言います。
$$
\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}
$$
前節では"make_dot()"による計算グラフを作成しましたが、正直見にくいため連鎖律も含めて計算グラフを下図の通り作成しました。下図より下記が理解できます。
損失$${loss=(y-y_{c})^2}$$をDとしたときwの勾配:$${\frac{dD}{dw}}$$、bの勾配:$${\frac{dD}{db}}$$は各演算(+-×÷など)の微分の積算で計算できる
足し算(+)や引き算(-)の場合は勾配に影響はなく、掛け算の場合はかけられた値と同倍になる
$$
\frac{dD}{dw}=2x×(y-y_{c})=2x×(正解値と予測値の差分)
$$
$$
\frac{dD}{db}=2×(y-y_{c})=2×(正解値と予測値の差分)
$$

5-3.勾配をPytorchで計算/確認
前節より重みwとバイアスbの勾配を手動で計算して確認しました。
[IN]
y_diff = y_pred-y_label #予測値と正解値の差分を計算
dLdw = 2*x*y_diff #重みの勾配を計算
dLdb = 2*y_diff #バイアスの勾配を計算
print('dL/dw(重みの勾配)', dLdw.mean())
print('dL/db(バイアスの勾配)', dLdb.mean())
pd.set_option('float_format', '{:.2f}'.format) #小数点以下2桁表示
df = pd.DataFrame({'x':x,
'w(重み)':torch.ones(len(x))*w.item(),
'b(バイアス)':torch.ones(len(x))*b.item(), #スカラー値はitem()でデータ抽出
'y_pred':y_pred.detach().numpy(),
'y_label':y_label.detach().numpy(),
'y_diff':y_diff.detach().numpy(),
'dLdw':dLdw.detach().numpy(),
'dLdb':dLdb.detach().numpy()})
display(df)
[OUT]
dL/dw(重みの勾配) tensor(-14.7817, grad_fn=<MeanBackward0>)
dL/db(バイアスの勾配) tensor(1.6475, grad_fn=<MeanBackward0>)結果として計算したwとbの勾配は"loss.backward()"後の"w.grad, b.grad"と同じ値であることを確認できました。また結果から判断して実際のmean()に関しては各入力値の勾配を計算後に平均値取得していると思います。

5-4.全結合での入力値を正規化する理由
一般的に「NNでは入力値が「0~1」または「-1~1」で高性能」と言われておりますが、その意味を逆伝搬の視点で考えます。
下記の通り線形モデルにおいてwとbの勾配(更新量)は入力値x倍だけ異なります。入力値が100だとしたら勾配は100倍異なるため更新されるパラメータの桁が大きく変わります。正規化することで勾配に極端な差が出ないようして学習しやすくすることがポイントだと思います。
$$
\frac{dD}{dw}=2x×(y-y_{c})=2x×(正解値と予測値の差分)
$$
$$
\frac{dD}{db}=2×(y-y_{c})=2×(正解値と予測値の差分)
$$
6.パラメータの更新による最適値検索
6-1.コード確認
最後に勾配を元のパラメータから更新していくことでモデルを学習させます。通常のPytorchでは「パラメータ更新のための最適化関数(optimizer)」や「専用の目的関数(損失関数)をモジュールから使用」したりしますが、今回は分かりやすさを重視してスクラッチで作成しました。
学習率ηはちょうどよい速度になるように0.01で調整しましたが通常はハイパーパラメータになるため自分で最適な値を見つける必要があります。
なお3章で記載の通り目標値は「w=5.34, b=0.18」です。
[IN]
lr = 0.01 #学習率
torch.manual_seed(0) #乱数のシードを設定
w = torch.randn(1, requires_grad=True) #重みを設定:ランダム値Ver.
b = torch.tensor(1.0, requires_grad=True) #バイアスを設定:固定値Ver.
epochs = 120 #学習回数
logs = {'epoch':[], 'wight':[], 'bias':[], 'loss':[]} #学習結果を格納する辞書
for epoch in range(epochs+1):
y_pred = pred(x) #予測値を計算
loss = mean_squared_error(y_pred, y_label) #平均二乗誤差を計算
loss.backward() #勾配を計算
with torch.no_grad():
w -= lr * w.grad #重みを更新
b -= lr * b.grad #バイアスを更新
#勾配の初期化
w.grad.zero_()
b.grad.zero_()
if epoch%10 == 0:
logs['epoch'].append(epoch) #学習回数を格納
logs['wight'].append(w.item()) #重みを格納
logs['bias'].append(b.item()) #バイアスを格納
logs['loss'].append(loss.item()) #損失関数を格納
print(f'重みw:{w.item():.2f}, バイアスb:{b.item():.3f}, loss:{loss.item():.3f}')
df = pd.DataFrame(logs).T
df.T
[OUT]
重みw:5.25, バイアスb:0.248, loss:0.929
結果としてかなり近い値まで得ることが出来ました。なお300回では「重みw:5.34, バイアスb:0.178, loss:0.909」のためepoch数を増やせば理論値に近づきます。
6-2.パラメータ変化の可視化(Animation)
参考までに勾配の変化はアニメーションで可視化しました。
[IN]
import numpy as np
import os
import matplotlib.pyplot as plt
import matplotlib.animation as animation
fig = plt.figure(figsize=(6,6))
def linearplot(fnum):
plt.cla()
epoch, w, b, loss = fnum*10, logs['wight'][fnum], logs['bias'][fnum], logs['loss'][fnum]
y = w*x + b
im = plt.scatter(x, y_label, label='y_label') #散布図を描画
im = plt.plot(x, y, label='y_pred') #直線を描画
plt.text(0.5, -1, f'epoch{epoch}, loss{loss:.2f}', fontsize=12) #テキストを描画
plt.text(0.5, -2, f'w:{w:.2f}, b:{b:.2f}', fontsize=12) #テキストを描画
plt.grid()
ani = animation.FuncAnimation(fig, linearplot, interval=500, frames=len(logs['epoch'])) #
from IPython.display import HTML
HTML(ani.to_html5_video())
# if not os.path.exists('gif'):
# os.mkdir('gif')
# print('gifフォルダを作成しました。')
# ani.save('gif/Anim1_傾きの変化確認.gif', writer='pillow') #アニメーションを保存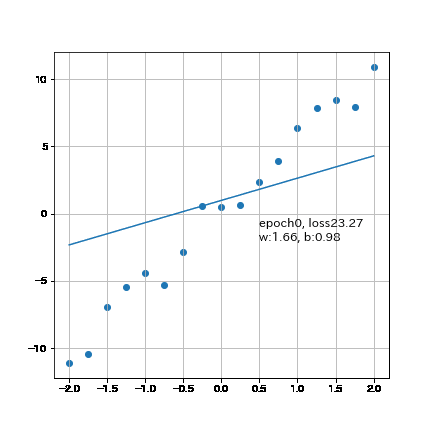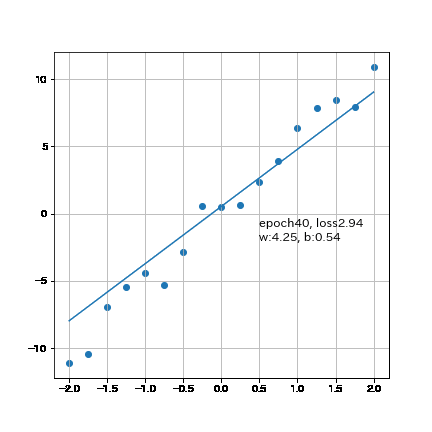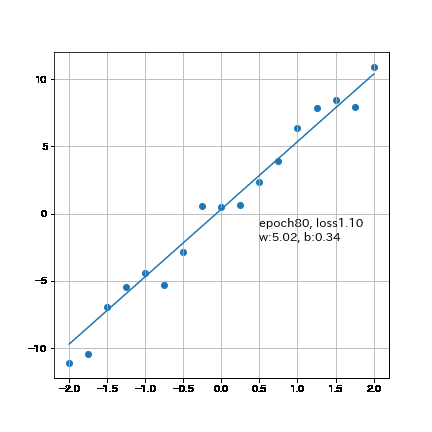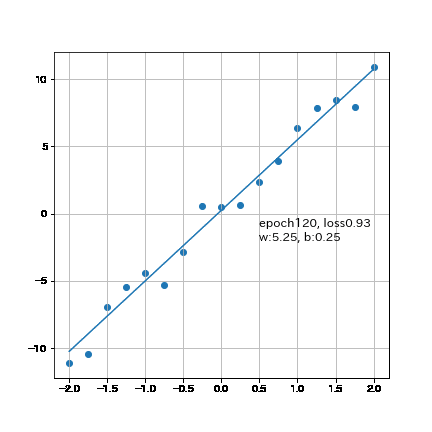
参考資料1:技術
あとがき
このままPytorchの基礎の記事は完成させたい!
この記事が気に入ったらサポートをしてみませんか?
