Pythonでやってみた(Engineering)：マルコフ連鎖／MCMC

１．概要

　本記事ではマルコフ連鎖およびマルコフ連鎖モンテカルロ法（Markov chain Monte Carlo methods：MCMC）を紹介します。
　理解が難しく間違っている可能性もあります確実に正しいことと理解出来たタイミングで有償化する予定です。

１－１．応用事例：マルコフ連鎖

　マルコフ連鎖の応用事例の一部として下記があります。確率的なプロセス／シミュレーションのため適用事例はモンテカルロ法と一部類似してます。

1. 自然言語処理：文章や単語の生成にマルコフ連鎖が利用されます。たとえば、特定の単語の次にどの単語が来る可能性が最も高いかを予測するのに使われます。

2. 検索エンジンのランキング：GoogleのPageRankアルゴリズムはマルコフ連鎖を用いてウェブページの重要性を評価します。

3. 金融工学：株価や金利などの金融商品の価格変動を予測するのにマルコフ連鎖が用いられます。

4. 生物学：遺伝子配列やタンパク質の構造を予測するのにマルコフ連鎖が用いられます。

5. 物理学：熱力学や統計力学におけるランダムな粒子の運動を表現するためにマルコフ連鎖が用いられます。

１－２．応用事例：マルコフ連鎖モンテカルロ法 (MCMC)

　MCMCの応用事例として下記があります。

• 統計学：ベイズ統計学において、事後分布からのサンプリングを行うためにMCMCがよく使われます。これにより、事後分布の形状に基づいてパラメータの不確実性を定量的に評価することが可能になります。

• 機械学習：MCMCは、複雑な確率モデルのパラメータ推定や予測分布の計算に用いられます。例えば深層学習のベイズ的な解釈やガウス過程、トピックモデルなどに使われます。

２．基礎知識・用語

　まずは押さえておきたい用語を紹介します。

２－１．確率過程（Stochastic Process）

　確率過程は時間とともに変動する偶然現象（確率的に変化する現象）を記述するための数学モデルです。マルコフ連鎖やマルコフ決定過程は特定の種類の確率過程です。

出典：12 群（電子情報通信基礎）-- 3 編（統計・確率）

２－２．確率モデル（Probabilistic Model）

　データ生成プロセスを表現するための統計モデルで確率論の概念を使用しています。マルコフモデルは一連の確率的な出来事をモデル化するための確率モデルの一つです。

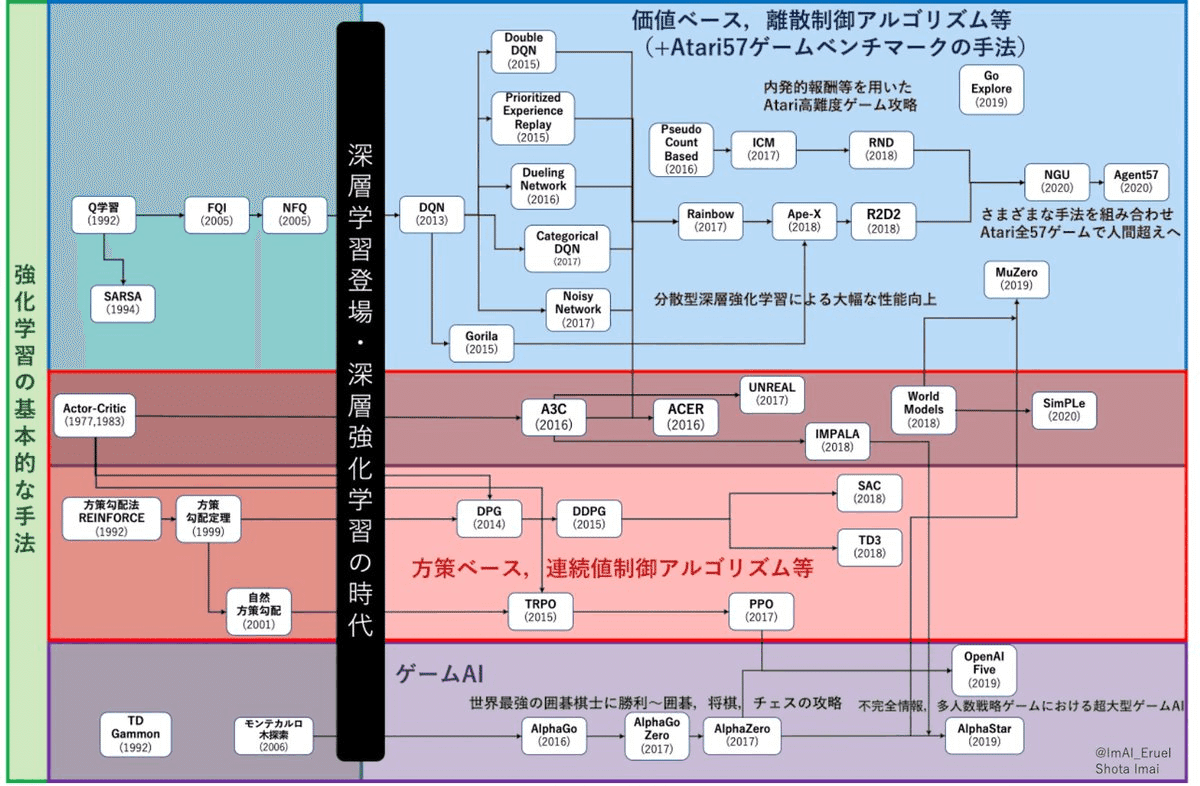
２－３．マルコフ決定過程（MDP）

　マルコフ決定過程（MDP）はマルコフ連鎖を拡張したものであり、特に強化学習で重要な意味を持ちます。
　MDPは強化学習のためエージェント（行動する対象）は行動を選択しますが、マルコフ連鎖では確率的（ランダム）です。またMDPは報酬の最大化を目的とする行動方針を見つけますが、マルコフ連鎖は確率的な振る舞いのみです。よって名前は似てますが用途は大きく異なります。

1. 状態（States）: エージェントが存在できる状況を表します。状態は、問題の状況やエージェントの位置を表すことができます。

2. 行動（Actions）: エージェントが状態において取ることのできる行動です。行動は、エージェントが状況を変更する方法を提供します。

3. 遷移確率（Transition Probabilities）: 行動をとったときに、ある状態から別の状態に移る確率を表します。これは、遷移確率行列で表現されることが一般的です。行列の要素は、特定の状態・行動ペアに対応する次の状態への遷移確率を示します。

4. 報酬関数（Reward Function）: 状態・行動ペアに対応する報酬を表します。報酬は、エージェントが目指すべき目標を定義し、通常はエージェントが最大化しようとするものです。

強化学習の基礎まとめ - Qiita

Shota Imai@えるエル

ゼロから作るDeep Learning ❹

３．マルコフ連鎖

　マルコフ連鎖とは、現在の状態が前の状態にのみ依存するような確率的な過程のことを指します。
　数式で記載すると下記の通りであり、前の条件(条件付き確率の条件の方)がどのようなもの($${X_1 = x_1,X_2 = x_2, ..., X_n = x_n}$$)であれ、次の確率$${ P(X_{n+1})}$$は直前の状態$${ X_n = x_n}$$のみに依存します。

$$
P(X_{n+1} = x | X_1 = x_1,X_2 = x_2, ..., X_n = x_n) = P(X_{n+1} = x | X_n = x_n)
$$

　例えば天気の変化はマルコフ連鎖で前日の天気に基づいて次の日の天気を予測するモデル作成ができます。また文章を形態素解析することで連続する文字における次の文字を確率的に選択することで文章生成もできます。

３－１．マルコフ連鎖の特性

　マルコフ連鎖は特性をもち、特に重要なものがマルコフ性となります。

• マルコフ性（無記憶性）：次の状態が現在の状態にのみ依存するという特性です。これは、「過去の情報」や「現在の状態から見た未来の情報」が次の状態に影響を与えないということを意味します。

  • サイコロの例では、1が連続で10回出ても次に1が出る確率は今の状態のみに依存する（1が出る確率は変わらない）

  • 天気の例では、数日前の天気がなんであれ”明日の天気の確率”は当日の天気の状態のみに依存する（$${P(S_{t+1}|S_t)}$$）

• 遷移確率は一定：状態間の遷移確率は時間に依存せず、現在の状態にのみ依存します。よって遷移確率は定数であり、これらを行列として表したものが遷移確率行列と言います。

• エルゴード性：マルコフ連鎖を無限回数（長期的に）実行すると、ある特定の条件下では一定の状態分布（確率分布）に収束し、収束した確率分布を定常分布と呼びます。この長期的な状態分布：定常分布は初期状態に依存しないという特性があり、これをエルゴード性と呼びます。エルゴード性には下記３つの条件が必要です。

  1. 任意の状態から他の任意の状態へ到達可能(accessible)

  2. 周期性を持たない

  3. 状態数が有限

３－２．遷移核と遷移確率行列

　遷移核（Transition Kernel）とは状態が連続的（無限の状態が存在する）でのマルコフ連鎖において、一つの状態から次の状態への遷移確率を表し、一般的に遷移確率は確率密度関数(分布)を使用します。具体的には、マルコフ連鎖において現在の状態がxであるとき次の状態がyとなる確率を考えます。これを遷移確率といい、これが全てのyについての分布を形成します。

　遷移確率行列 (Transition Probability Matrix)とは、天気やサイコロのような状態が離散的（有限の状態しか存在しない）におけるマルコフ連鎖を扱う場合で使用します。「遷移確率行列の各行の和は1」となります。

$$
P =
\begin{pmatrix}
P_{11} & P_{12} & \cdots & P_{1n} \\
P_{21} & P_{22} & \cdots & P_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
P_{n1} & P_{n2} & \cdots & P_{nn}
\end{pmatrix}
$$

　下表は天気を例として状態$${i}$$から$${j}$$へ遷移する遷移確率行列です。

　なお状態$${X_n}$$がとりえる値の集合は状態空間$${S}$と呼ばれ、天気の例だとS={晴れ, 曇り, 雨}となります。

３－３．定常分布

　３－３－１．定常分布の定義

　マルコフ連鎖において、連鎖のステップ数を無限大に増やすと状態の分布は特定の確率分布に収束していきます。この収束した分布を定常分布（Stationary Distribution）と呼びます。定常分布は一般的にベクトル$${\pi}$$で表します。

$$
\pi = \begin{pmatrix} \pi_{1} \\ \pi_{2} \\ \vdots \\ \pi_{n} \end{pmatrix} 
$$

　マルコフ連鎖がエルゴード性（任意の状態から任意の状態への遷移が可能な性質）を持つ場合、このような定常分布への収束が見られます。
　例えば、天気のマルコフ連鎖をシミュレーションした場合、時間経過とともに各天気の確率が一定になり（定常分布になる）ことが確認できます。定常分布では全ての状態の確率の合計が1になります。

$$
 \begin{pmatrix} \pi_1 \\ \pi_2 \\ \vdots \\ \pi_n \end{pmatrix}^T \begin{pmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{pmatrix} =\pi_1 + \pi_2+\dots+\pi_n= 1 
$$

　３－３－２．定常分布と遷移確率行列の関係

　前述の通りマルコフ連鎖（遷移確率行列）は定常分布に収束する性質があります。これは定常分布ベクトル（$${\pi}$$）を左から遷移確率行列（$${P}$$）と掛けると再び定常分布ベクトルが得られる$${\pi=\pi\cdot P}$$という性質です。

$$
\begin{pmatrix} \pi_1 \\ \pi_2 \\ \vdots \\ \pi_n \end{pmatrix} = \begin{pmatrix} \pi_1 & \pi_2 & \cdots & \pi_n \end{pmatrix} \begin{pmatrix} P_{1,1} & P_{1,2} & \cdots & P_{1,n} \\ P_{2,1} & P_{2,2} & \cdots & P_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ P_{n,1} & P_{n,2} & \cdots & P_{n,n} \end{pmatrix} 
$$

３－４．詳細つり合い

　詳細つり合い（Detailed Balance）とは、連鎖がある定常分布に収束する時に、その分布が「任意の状態$${i}$$から状態$${j}$$への遷移確率と状態$${j}$$から状態$${i}$$への遷移確率がつり合う」という性質を指します。
　詳細釣り合い条件は以下の式で表されます。

$$
P(j|i)π(i) = P(i|j)π(j)
$$

• $${π(i)}$$：状態$${i}$$の定常確率（状態$${i}$$になる確率）

• $${P(j|i)}$$：状態$${i}$$から状態$${j}$$に遷移する（条件付き）確率

　概念として、工学系におけるマスバランス／熱収支に近いものと思います。「定常状態である＝見かけ上の変化がない＝流入と流出が等しい」ため、「状態A-＞状態Bへの遷移(量）」と「状態B->状態Aへの遷移（量）」が等しいと理解できます。

　これを天気の例に適用すると、詳細釣り合い条件では「晴れから曇りへの遷移」と「曇りから晴れへの遷移」が釣り合う状態となります（例：$${P(曇り|晴れ)\pi(晴れ) = P(晴れ|曇り)\pi(曇り) }$$）。これが成り立つとき、マルコフ連鎖は定常分布に収束し詳細つり合い条件が満たされると言えます。

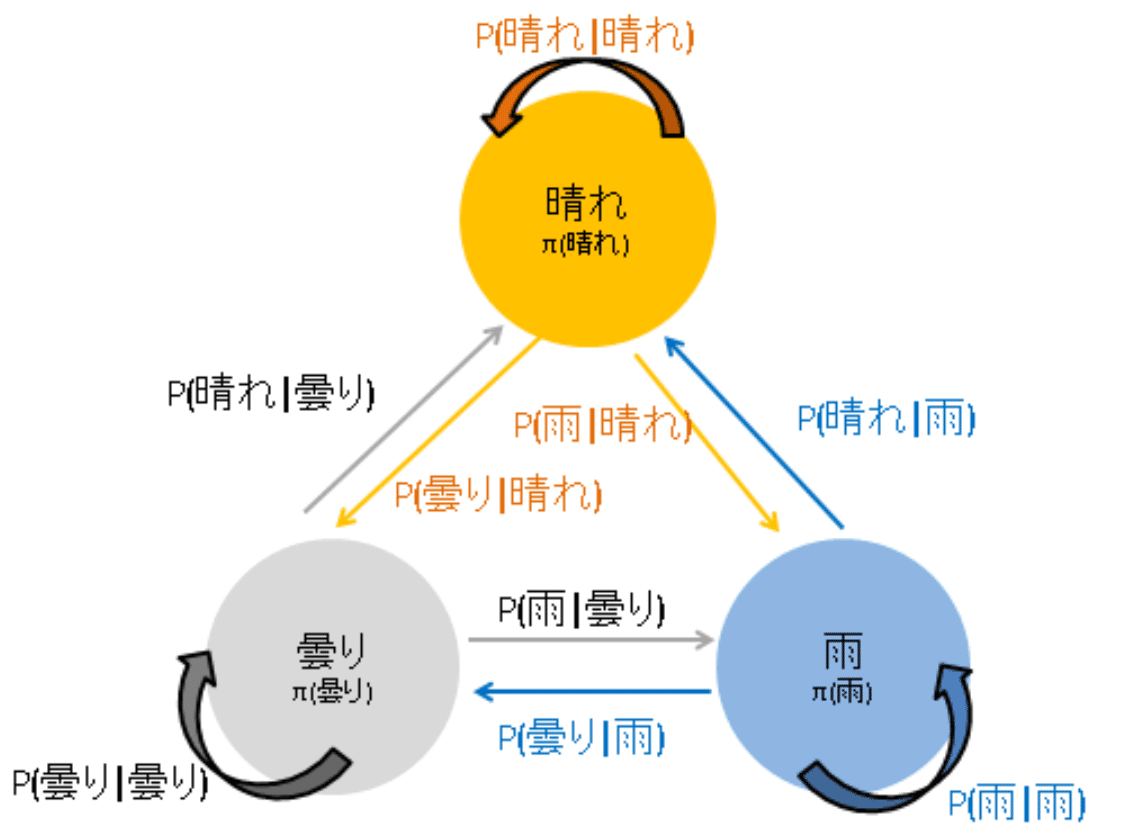
　詳細つり合い条件は定常分布を求めるための重要なツールとなります。それはこの条件が成り立つと状態の確率が時間と共に変わらない定常分布に収束するからです。
　詳細つり合いが成り立つことで、マルコフ連鎖モンテカルロ法（MCMC）などの統計的な手法を用いたシミュレーションが可能となります。

３－５．詳細釣り合いの更なる理解へ

　詳細釣り合いを理解するために部屋⇔外の滞在／移動確率をシミュレーションしてみます。概要まとめは下図の通りです。

　シミュレーションの条件として遷移確率行列$${P}$$は下記の通りです。

$$
P=\begin{pmatrix} P_{11} & P_{12} \\ P_{21} & P_{22} \end{pmatrix}
=\begin{pmatrix} P(部屋|部屋) & P(外|部屋) \\ P(部屋|外) & P(外|外)\end{pmatrix}
$$

　Pythonで移動・滞在回数を1,000回としてシミュレーションしました。結果として定常分布$${\pi}$$は下記の結果となりました。

$$
\pi=\begin{pmatrix} \pi_1 \\ \pi_2 \end{pmatrix}=\begin{pmatrix} \pi(部屋) \\ \pi(外) \end{pmatrix}=\begin{pmatrix} 0.565 \\ 0.435 \end{pmatrix}
$$

[IN]
# 状態を定義 (0:部屋, 1:外)
states = ["部屋", "外"]

# 遷移確率行列を定義
P = np.array([[0.7, 0.3],
              [0.4, 0.6]])

# シミュレーションの日数を設定
N = 1000

# 初期状態（部屋）を設定
place = [0]

# マルコフ連鎖のシミュレーション
for _ in range(N-1):
    current_state = place[-1] # 現在の状態を取得
    next_state = np.random.choice([0, 1], p=P[current_state]) #遷移確率行列から次の状態をサンプリング
    place.append(next_state)

print(f'シミュレーション後のデータ数：{len(place)}')
# 各状態の推移を格納するリストを準備
inside, outside = [], []

# 各状態の推移を計算
for i in range(N):
    inside.append(place[:i+1].count(0) / len(place[:i+1]))
    outside.append(place[:i+1].count(1) / len(place[:i+1]))

print(f'各推移のデータ数　部屋：{len(inside)}, 外：{len(outside)}')
print(f'最終的な各状態の確率　部屋：{inside[-1]}, 外：{outside[-1]}')

# 可視化
fig, ax = plt.subplots(figsize=(10, 7), facecolor="white")
ax.plot(inside, label="部屋")
ax.plot(outside, label="外")
ax.set(xlabel="時間", ylabel="現在値の確率", title="マルコフ連鎖のシミュレーション", 
       xticks=range(0, N+100, 100), yticks=np.arange(0, 1.1, 0.1))
ax.legend(), ax.grid()
plt.show()

[OUT]
シミュレーション後のデータ数：1000
各推移のデータ数　部屋：1000, 外：1000
最終的な各状態の確率　部屋：0.565, 外：0.435

　得られた定常分布$${\pi}$$と遷移確率行列$${P}$$から下記２つを確認できました。

• 定常分布の行列方程式：$${\pi=\pi \cdot P}$$

• 詳細釣り合い：$${P(j|i)π(i) = P(i|j)π(j)}$$

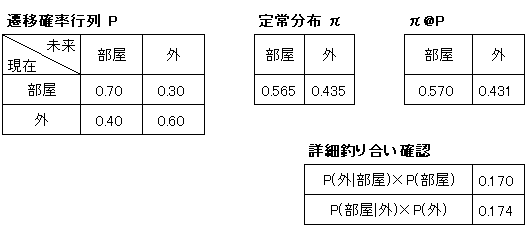
　定常分布の行列方程式をシミュレーションで確認しましたが、解析的に計算も可能です。定常分布の行列式は下記の通りです。

$$
\begin{pmatrix} \pi_1 & \pi_2 \end{pmatrix} \begin{pmatrix} P_{11} & P_{12} \\ P_{21} & P_{22} \end{pmatrix}
= \begin{pmatrix} \pi_1 & \pi_2 \end{pmatrix}
$$

　上式を展開すると下記の通りです。結果として両式で$${\pi_2= \frac{3}{4}\pi_1}$$が得られました。

$$
\begin{cases}
式1：\pi_1P_{11} + \pi_2P_{21} =0.7\pi_1 + 0.4\pi_2= \pi_1\\
式2：\pi_1P_{12} + \pi_2P_{22} =0.3\pi_1 + 0.6\pi_2= \pi_2 
\end{cases}
$$

$$
\begin{cases}
式1：\pi_2= \frac{3}{4}\pi_1 \\
式2：\pi_2= \frac{3}{4}\pi_1
\end{cases}
$$

式3：$${\pi_1+\pi_2=1}$$と組み合わせると下記が得られます。これで計算すると詳細釣り合い、定常分布の行列方程式は完全に一致しており定常性が確認できました。

• $${\pi_1=\pi(部屋)=\frac{4}{7}}=0.5714$$

• $${\pi_2=\pi(外)=\frac{3}{7}}=0.4286$$

【定常分布の行列方程式の再確認】
　遷移確率行列$${P}$$を再掲載します。

$$
\begin{pmatrix} \pi_1 & \pi_2 \end{pmatrix} \begin{pmatrix} P_{11} & P_{12} \\ P_{21} & P_{22} \end{pmatrix}
= \begin{pmatrix} \pi_1 & \pi_2 \end{pmatrix}
$$

　式１を再度文字に置き換えて確認します。

$$
\pi_1P_{11} + \pi_2P_{21} = \pi_1 \\ \rightarrow \pi(部屋)P(部屋|部屋)+\pi(外)P(部屋|外)=\pi(部屋)\\
\rightarrow 確率_{部屋から部屋} + 確率_{外から部屋} = 確率_{部屋}
$$

　上記より部屋という一つの系で考えた時に存在する確率（数・時間）は部屋に入ってくる確率とバランス（収支）がとれていると理解できます。つまり定常分布の行列方程式は確率の収支をとっているものと理解できます。　
　この条件を満たすために詳細釣り合い$${P(j|i)π(i) = P(i|j)π(j)}$$を満たす必要があります。この詳細釣り合いは部分的（ミクロ）な収支が釣り合いを見ていると思います。

４．マルコフ連鎖シミュレーション：天気の推移

　当日の天気がある条件においる翌日の天気の確率（条件付き確率）が下記の通りだとします。この時各天気の確率がどのように収束するかシミュレーションしました。
　結果としては$${P(晴れ)}=0.39$$, $${P(曇り)}=0.30$$, $${P(雨)}=0.31$$となりました。

４－１．シミュレーション条件

　シミュレーションの条件は下記の通りです。

【遷移確率行列】

$$
\begin{aligned}
\bf P&=\begin{bmatrix} P_{11} & P_{12} & P_{13} \\ P_{21} & P_{22} & P_{23} \\ P_{31} & P_{32} & P_{33} \end{bmatrix} \\
&=\begin{bmatrix}
P(S_{t+1}=S|S_t=S) & P(S_{t+1}=C|S_t=S) & P(S_{t+1}=R|S_t=S) \\
P(S_{t+1}=S|S_t=C) & P(S_{t+1}=C|S_t=C) & P(S_{t+1}=R|S_t=C) \\
P(S_{t+1}=S|S_t=R) & P(S_{t+1}=C|S_t=R) & P(S_{t+1}=R|S_t=R)
\end{bmatrix}
\\&=\begin{bmatrix}
0.7 & 0.2 & 0.1 \\
0.3 & 0.4 & 0.3 \\
0.1 & 0.4 & 0.5
\end{bmatrix}
\end{aligned}
$$

• $${P(S_{t+1}=S|S_t=S)}$$：当日が晴れ(Sunny)、翌日が晴れ(Sunny)

• $${P(S_{t+1}=C|S_t=S)}$$：当日が曇り(Cloudy)、翌日が晴れ(Sunny)

• $${P(S_{t+1}=R|S_t=S)}$$：当日が雨(Rainy)、翌日が晴れ(Sunny)

• $${P(S_{t+1}=S|S_t=C)}$$：当日が晴れ(Sunny)、翌日が曇り(Cloudy)

• $${P(S_{t+1}=C|S_t=C)}$$：当日が曇り(Cloudy)、翌日が曇り(Cloudy)

• $${P(S_{t+1}=R|S_t=C)}$$：当日が雨(Rainy)、翌日が曇り(Cloudy)

• $${P(S_{t+1}=S|S_t=R)}$$：当日が晴れ(Sunny)、翌日が雨(Rainy)

• $${P(S_{t+1}=C|S_t=R)}$$：当日が曇り(Cloudy)、翌日が雨(Rainy)

• $${P(S_{t+1}=R|S_t=R)}$$：当日が雨(Rainy)、翌日が雨(Rainy)

４ー２．可視化：確率の収束

　確率が一定の値に収束するのを可視化しました。

[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import seaborn as sns
import japanize_matplotlib
import scipy.stats as stats

# 状態を定義 (0:晴れ, 1:曇り, 2:雨)
states = ["晴れ", "曇り", "雨"]

# 遷移確率行列を定義
P = np.array([[0.7, 0.2, 0.1],
              [0.3, 0.4, 0.3],
              [0.1, 0.4, 0.5]])

# シミュレーションの日数を設定
N = 1000

# 初期状態（晴れ）を設定
weather = [0]

# マルコフ連鎖のシミュレーション
for _ in range(N-1):
    current_state = weather[-1] # 現在の状態を取得
    next_state = np.random.choice([0, 1, 2], p=P[current_state]) #遷移確率行列から次の状態をサンプリング
    weather.append(next_state)

print(f'シミュレーション後のデータ数：{len(weather)}')
# 各状態の推移を格納するリストを準備
sunny, cloudy, rainy = [], [], []

# 各状態の推移を計算
for i in range(N):
    sunny.append(weather[:i+1].count(0) / len(weather[:i+1]))
    cloudy.append(weather[:i+1].count(1) / len(weather[:i+1]))
    rainy.append(weather[:i+1].count(2) / len(weather[:i+1]))

print(f'各推移のデータ数　晴れ：{len(sunny)}, 曇り：{len(cloudy)}, 雨：{len(rainy)}')
print(f'最終的な各状態の確率　晴れ：{sunny[-1]}, 曇り：{cloudy[-1]}, 雨：{rainy[-1]}')

# 可視化
fig, ax = plt.subplots(figsize=(10, 7), facecolor="white")
ax.plot(sunny, label="晴れ")
ax.plot(cloudy, label="曇り")
ax.plot(rainy, label="雨")
ax.set(xlabel="日数", ylabel="各天気の確率", title="マルコフ連鎖のシミュレーション", 
       xticks=range(0, N+100, 100), yticks=np.arange(0, 1.1, 0.1))
ax.legend(), ax.grid()
plt.show()

[OUT]
シミュレーション後のデータ数：1000
各推移のデータ数　晴れ：1000, 曇り：1000, 雨：1000
最終的な各状態の確率　晴れ：0.387, 曇り：0.299, 雨：0.314

４ー３．可視化：定常分布

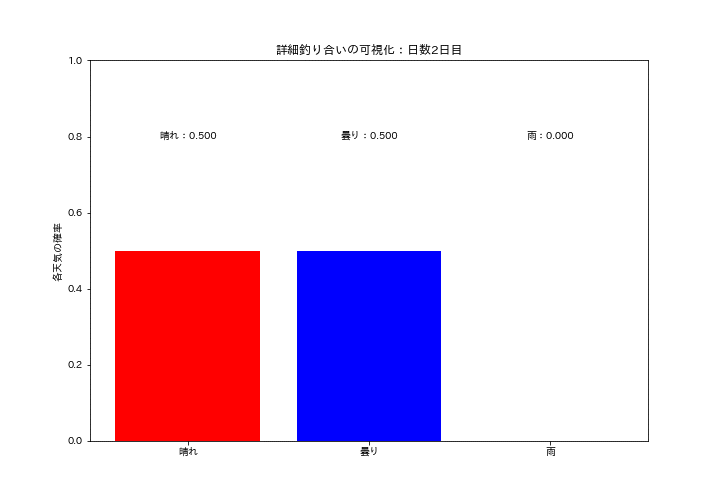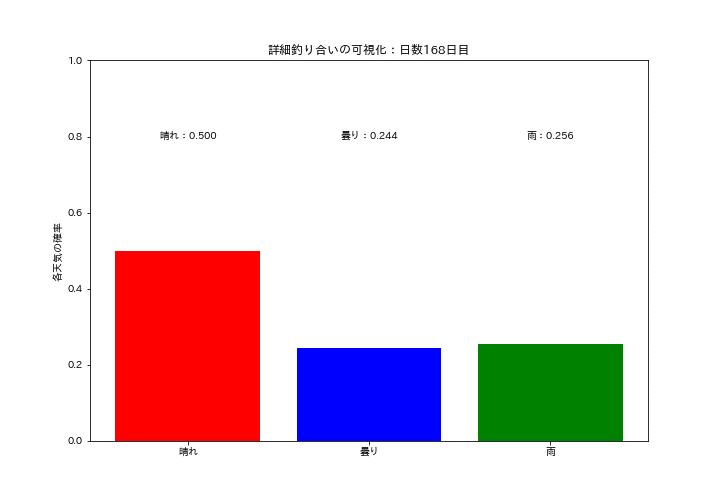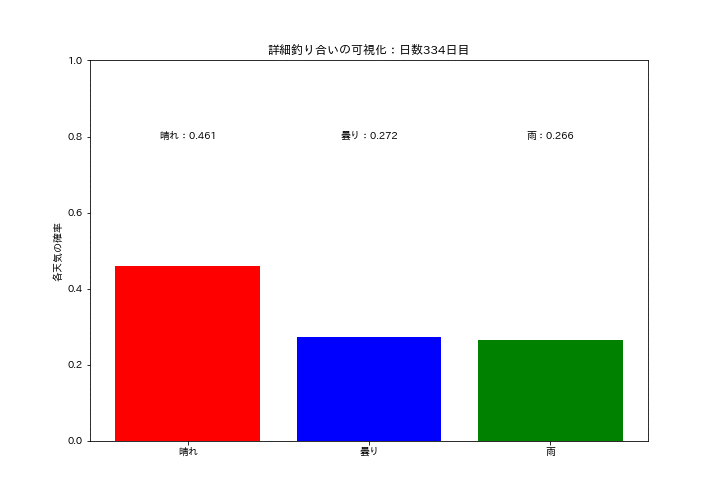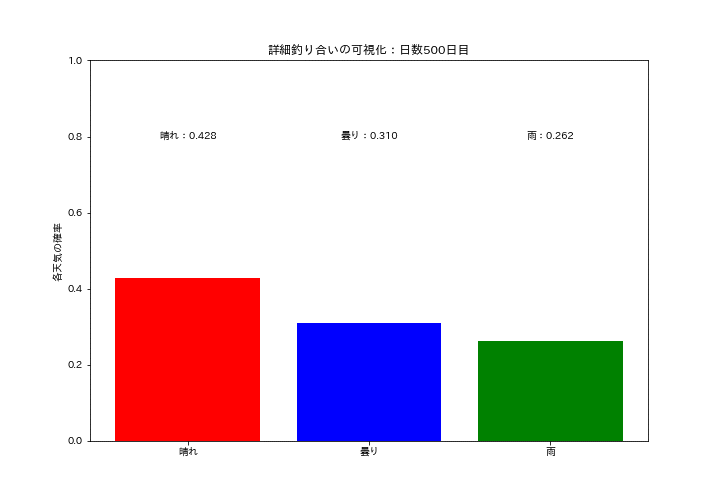
　各天気の確率質量分布が一定の値に収束していくのを可視化しました。初期は確率がバラバラですが、時間が経つにつれて分布が変化しなくなり定常分布になっていることが確認できます。

[IN]
fig, ax = plt.subplots(figsize=(10, 7), facecolor="white")

def init():
    ax.grid()

def show_detailed_balance(i):
    ax.cla()
    data = [sunny[i], cloudy[i], rainy[i]]
    ax.bar(states, data, color=["red", "blue", "green"])
    ax.set_title(f'詳細釣り合いの可視化：日数{i+1}日目')
    ax.text(0.0, 0.8, f'晴れ：{data[0]:.3f}', ha='center', va='center', color="black")
    ax.text(1.0, 0.8, f'曇り：{data[1]:.3f}', ha='center', va='center', color="black")
    ax.text(2.0, 0.8, f'雨：{data[2]:.3f}', ha='center', va='center', color="black")
    ax.set(ylabel="各天気の確率", ylim=(0, 1))

N = 500
ani = animation.FuncAnimation(fig, show_detailed_balance, init_func=init, frames=range(1,N,2), interval=10)
ani.save("detailed_balance.gif", writer="Pollow")
plt.legend()
plt.show()
    
[OUT]

４－４．解析計算

　シミュレーションではなく手計算でも解析解を解き下記を確認します。

• 定常分布の行列方程式：$${\pi=\pi \cdot P}$$

• 詳細釣り合い：$${P(j|i)π(i) = P(i|j)π(j)}$$

$$
\pi = \begin{pmatrix} \pi_{1} \\ \pi_{2} \\ \pi_{3} \end{pmatrix}
=\begin{pmatrix} \pi_{晴} \\ \pi_{曇} \\ \pi_{雨} \end{pmatrix}
$$

$$
\begin{aligned}
\bf P&=\begin{bmatrix} P_{11} & P_{12} & P_{13} \\ P_{21} & P_{22} & P_{23} \\ P_{31} & P_{32} & P_{33} \end{bmatrix}=\begin{bmatrix}
0.7 & 0.2 & 0.1 \\
0.3 & 0.4 & 0.3 \\
0.1 & 0.4 & 0.5
\end{bmatrix}
\end{aligned}
$$

　「定常分布の行列方程式」および「定常分布の確率和=1（$${\pi_{\text{晴}}+ \pi_{\text{曇}}+ \pi_{\text{雨}}=1}$$）」より計算式は下記の通りです。

$$
\begin{cases}
式1：0.7\pi_{\text{晴}} + 0.3\pi_{\text{曇}} + 0.1\pi_{\text{雨}} = \pi_{\text{晴}}\\ 式2：0.2\pi_{\text{晴}} + 0.4\pi_{\text{曇}} + 0.4\pi_{\text{雨}} = \pi_{\text{曇}}\\ 式3：0.1\pi_{\text{晴}} + 0.3\pi_{\text{曇}} + 0.5\pi_{\text{雨}} = \pi_{\text{雨}}\\ 式4：\pi_{\text{晴}} + \pi_{\text{曇}} + \pi_{\text{雨}} = 1 \end{cases}
$$

　上記の連立方程式はsympyを用いて解きました。なお変数が3つに対して式が4つあるため、式3を除外しました。結果として定常分布ベクトル$${\pi}$$を得られました。

$$
\pi = \begin{pmatrix} \pi_{1} \\ \pi_{2} \\ \pi_{3} \end{pmatrix}
=\begin{pmatrix} \pi_{晴} \\ \pi_{曇} \\ \pi_{雨} \end{pmatrix}
=\begin{pmatrix} 0.4091 \\ 0.3182 \\ 0.2727 \end{pmatrix}
$$

[IN]
import sympy as sym

pi_1, pi_2, pi_3 = sym.symbols("pi_1, pi_2, pi_3")
P11, P12, P13 = sym.symbols("P11, P12, P13")
P21, P22, P23 = sym.symbols("P21, P22, P23")
P31, P32, P33 = sym.symbols("P31, P32, P33")
P11, P12, P13 = 0.7, 0.2, 0.1
P21, P22, P23 = 0.3, 0.4, 0.3
P31, P32, P33 = 0.1, 0.4, 0.5

eq1 = sym.Eq(pi_1*P11 + pi_2*P21 + pi_3*P31, pi_1)
eq2 = sym.Eq(pi_1*P12 + pi_2*P22 + pi_3*P32, pi_2)
eq3 = sym.Eq(pi_1*P13 + pi_2*P23 + pi_3*P33, pi_3)
eq4 = sym.Eq(pi_1 + pi_2 + pi_3, 1)
display(eq1, eq2, eq3, eq4)

sym.solve([eq1, eq2, eq4])

[OUT]
\displaystyle 0.2 \pi_{1} + 0.4 \pi_{2} + 0.4 \pi_{3} = \pi_{2}0.2π 
\displaystyle 0.1 \pi_{1} + 0.3 \pi_{2} + 0.5 \pi_{3} = \pi_{3}0.1π 
\displaystyle \pi_{1} + \pi_{2} + \pi_{3} = 1π 
{pi_1: 0.409090909090909, pi_2: 0.318181818181818, pi_3: 0.272727272727273}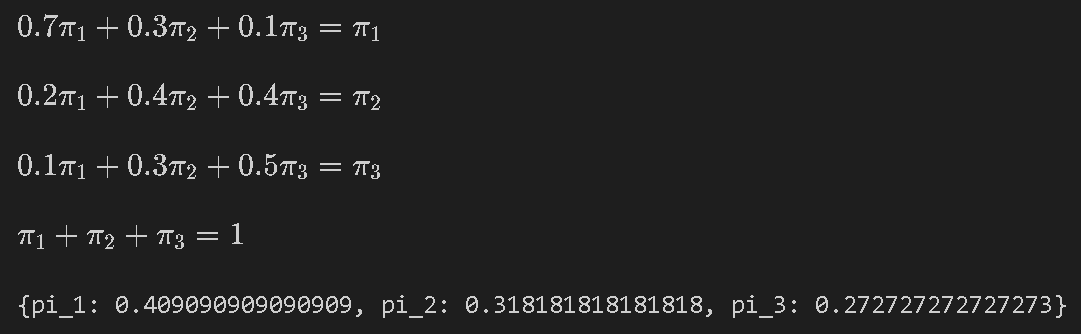

　まずは定常分布の行列方程式：$${\pi=\pi \cdot P}$$を確認したところ、計算式が成り立っており定常状態であることが確認できました。

　次に詳細釣り合い：$${P(j|i)π(i) = P(i|j)π(j)}$$を確認しました。各条件で完全に：$${P(j|i)π(i) = P(i|j)π(j)}$$は満たしておりませんが近い値は取っております。

５．棄却サンプリング

　マルコフ連鎖モンテカルロ法(MCMC)の説明に入る前に、棄却サンプリングというサンプリング手法を説明します。棄却サンプリングは、モンテカルロ法を用いて特定の確率分布からサンプリングを行う方法です。

　この方法の長所はその直感的な理解のしやすさです。しかし、高次元のデータに対しては「次元の呪い」の問題が生じ効率的なサンプリングが難しくなります。次元の呪いに対する対策としてマルコフ連鎖モンテカルロ法(MCMC)が使われますが、それについては次の章で説明します。

５－１．目標分布・提案分布

　棄却サンプリングにおいては、目標分布と提案分布という二つの用語が重要です。それぞれの意味を以下に説明します。

• 目標分布：分析者がサンプリングしたい確率分布を指します。機械学習においては、パラメータの事後分布が目標分布となることがよくあります。

• 提案分布：この分布は新しいサンプルを生成するために使われます。つまり、現在の状態から次の状態へ移るときに用いられる確率分布です。通常はサンプリングが容易な一様分布が用いられます。

５－２．棄却サンプリングのプロセス

　棄却サンプリングの一般的な手順は以下のとおりです。

1. 提案分布からランダムにサンプルを生成

2. 生成したサンプルが目標分布に基づいて受け入れられるかどうか判断

   • サンプルが受け入れられれば、そのサンプルを保持

   • サンプルが受け入れられなければ、そのサンプルを棄却

3. 1~2を所定の回数繰り返す

５－３．棄却サンプリングの実装(Python)

　Pythonを用いて棄却サンプリングを実装します。ライブラリを使用すれば簡単に実装できますが、ここでは標準正規分布からランダムに数値を取得して、得られたサンプリングデータが本当に正規分布に従っているかどうかを確認します。

　５－３－１．目標分布・提案分布の作成

　目標分布、提案分布はそれぞれ下記の通りです。

• 目標分布：標準正規分布（平均：０、分散：１）

• 提案分布：値が目標分布の最大値と同じ一様分布

$$
f(x)=\dfrac{1}{\sqrt{2\pi\sigma^2}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})
$$

[IN]
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from scipy.stats import norm, uniform

# 目標分布 (平均0, 標準偏差1の正規分布)
def target_dist(x):
    return norm.pdf(x, 0, 1)

# 提案分布 (一様分布)
def proposal_dist(x, max_y):
    loc, scale = -5, 10
    return uniform.pdf(x, -5, 10) * scale * max_y
    
#提案分布の上限設定
x = np.linspace(-5, 5, 100)
max_y = target_dist(x).max()

#可視化 
fig, axs = plt.subplots(1, 2, figsize=(10, 5), facecolor="white")
ax1, ax2 = axs[0], axs[1]

ax1.plot(x, target_dist(x), label="目標分布", color="green")
ax1.fill_between(x, 0, target_dist(x), color="green", alpha=0.3)
ax1.set(xlabel="x", ylabel="確率密度", title="目標分布", xticks=range(-5, 6), yticks=np.arange(0, 0.5, 0.1))
ax1.legend(), ax1.grid()

ax2.plot(x, proposal_dist(x, max_y), label="提案分布", color="orange")
ax2.fill_between(x, 0, proposal_dist(x, max_y), color="orange", alpha=0.3)
ax2.set(xlabel="x", ylabel="確率密度", title="提案分布", xticks=range(-5, 6), yticks=np.arange(0, 0.5, 0.1))
ax2.legend(), ax2.grid()
plt.show()

[OUT]

　５－３－２．棄却サンプリングの実装

　前述したプロセス通り棄却サンプリングを実装します。より具体的なフローは下記の通りです。

1. サンプリングの点を作成：欲しい範囲内、つまり分布の上限・下限に合わせて各次元の最大値・最小値を設定して、その中から一様乱数を生成

2. 生成したサンプルが目標分布に基づいて受け入れられるかどうかを判定

   • サンプルが受け入れられればそのサンプルを保持：acceptedに格納

   • サンプルが受け入れられなければそのサンプルを棄却：rejectedに格納

3. 1~2を所定の回数繰り返す

　結果より作成した乱数のうち約26.2%がサンプリングとして使用されました（残りは棄却）。

[IN]
np.random.seed(123)
# 棄却サンプリング
N = 1000
_x_sample = [np.random.uniform(x.min(), x.max()) for _ in range(N)]
_y_sample = [np.random.uniform(0, max_y) for _ in range(N)]
x_sample, y_sample = np.array(_x_sample), np.array(_y_sample)
print(f'サンプリングの範囲　x：{x_sample.min():.2f} ~ {x_sample.max():.2f}, y：{y_sample.min():.2f} ~ {y_sample.max():.2f}')
print(f'各次元のデータ数　X：{len(x_sample)}, Y：{len(y_sample)}')

# 棄却サンプリング
accepted = []
rejected = []

for i in range(N):
    if y_sample[i] <= target_dist(x_sample[i]):
        accepted.append((x_sample[i], y_sample[i]))
    else:
        rejected.append((x_sample[i], y_sample[i]))

accepted = np.array(accepted)
rejected = np.array(rejected)

# アニメーションの設定
fig, ax = plt.subplots(figsize=(10, 7), facecolor="white")

# 目標分布と提案分布のプロット
ax.plot(x, target_dist(x), label="目標分布", color="green")
ax.plot(x, proposal_dist(x, max_y), label="提案分布", color="orange")

# サンプルのプロット（初期設定）
scatter_accepted, = ax.plot([], [], 'o', color='blue', markersize=5, label='Accepted samples')
scatter_rejected, = ax.plot([], [], 'o', color='red', markersize=5, label='Rejected samples')

ax.set(xlim=(-5, 5), ylim=(0, max_y), xlabel="x", ylabel="確率密度", title="Rejection Sampling", xticks=range(-5, 6), yticks=np.arange(0, 0.5, 0.1))
ax.grid(), ax.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=12)

# アニメーション更新関数
def update(i):
    scatter_accepted.set_data(accepted[:i+1, 0], accepted[:i+1, 1])
    scatter_rejected.set_data(rejected[:i+1, 0], rejected[:i+1, 1])
    return scatter_accepted, scatter_rejected

# アニメーションの作成
ani = animation.FuncAnimation(fig, update, frames=range(1,N,3), interval=100, blit=True)

# アニメーションの保存
plt.tight_layout()
ani.save('rejection_sampling.gif', writer='pillow')

# アニメーションの表示
plt.show()

# 棄却サンプリングの結果
print(f'提案分布に入った乱数の割合：{len(accepted) / N*100:.1f}%')

[OUT]
サンプリングの範囲　x：-5.00 ~ 4.99, y：0.00 ~ 0.40
各次元のデータ数　X：1000, Y：1000
提案分布に入った乱数の割合：26.2%

　５－３－３．サンプリング結果の確認１：分布の可視化

　棄却サンプリングにより目標分布からサンプリングして、その数値を保持しました。これが本当に正規分布に従っているかどうか確認しました。
※サンプリングは各次元（x, y）をリストに格納していますが、使用するのはx軸のサンプルのみとなります。
　結果としてサンプリングしたデータは目標分布と同じ形であり正しく処理されていることが確認できました。

[IN]
print(f'10個のサンプル')
print(accepted[:10, 0])

fig, ax = plt.subplots(figsize=(10, 7), facecolor="white")
sns.histplot(accepted[:, 0], bins=30, color="blue", label="Accepted samples", ax=ax)

[OUT]
10個のサンプル
[ 1.96469186  0.51314769 -0.7689354  -0.19068099 -1.07882482 -0.61427755
 -1.01955745  0.31551374  0.31827587  1.11023511]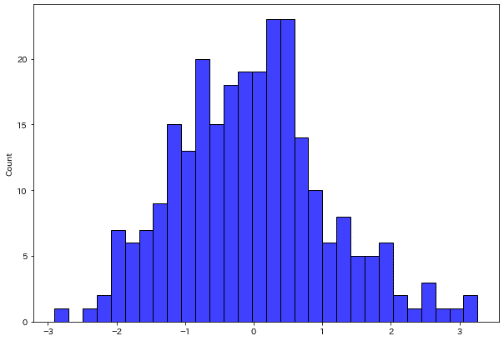

　５－３－４．サンプリング結果の確認２：Shapiro-Wilk検定

　参考としてShapiro-Wilk検定を紹介します。
　Shapiro-Wilk検定（正規性の検定）は、あるデータセットが正規分布から取得されたものであるかを確認するための統計的な検定方法の一つです。もしデータが正規分布に従っているという仮説が棄却されれば、データは正規分布から外れていると解釈します。

　検定の統計量Wは次の式で計算されます。検定の統計量Wの値は0から1までの範囲を取り、Wが1に近ければデータは正規分布に近いと解釈します。

$$
W = \frac{∑_{i=1}^{n} a_i x_{(i)})^2}{ ∑_{i=1}^{n} (x_i - x̄)^2} 
$$

• $${x_{(i)} }$$：ソートされたデータの i 番目の値

• $${x̄ }$$：全データの平均

• $${a_i}$$ ：正規分布から導かれる特定の重み

　説明は省略しますが、Wとは別に検定の統計量Wのp値が提供されます。これはデータが正規分布から取得されたものであるという仮説の下で、現在のW値あるいはそれ以上に極端なW値を取得する確率を表します。一般的に、p値に対して指定した閾値(0.05など)から判断します。注意点として検定のp値の棄却と符号が逆に感じることがあります。

• p<0.05の時、正規分布に従わないと判断

• p≧0.05の時、正規分布に従うと判断

　Pythonではscipy.statsモジュールのshapiro関数を使うとShapiro-Wilk検定を簡単に実装でき、p≧0.05のため統計学的に正規分布と判定できます。

[IN]
import numpy as np
from scipy import stats #Shapiro -Wilk検定
w, p = stats.shapiro(accepted[:, 0])
print(f'W値：{w:.3f}, p値：{p:.3f}')

[OUT]
W値：0.990, p値：0.079

Shapiro-Wilk検定（正規性の検定）

シャピロ–ウィルク検定 - Wikipedia

６．次元の呪い

　次元の呪いとは、次元が増えるにつれて計算量や必要なデータ量が指数的に増大する問題を指します。
　例えば棄却サンプリングではN次元空間をランダムにサンプリングしますが、次元数が増えると必要なサンプリング数が指数的に増加します。これは空間の広がりが指数的に大きくなるためです。

６－１．多変量ガウス分布で棄却サンプリング

　2次元の正規分布を使用した例から一歩進んで、ここでは3次元の正規分布（多変量ガウス分布）で棄却サンプリングを試してみます。

　1000個のサンプリングポイントのうち、目標分布（多変量ガウス分布）に入ったサンプリング点はわずか5個（0.5%）でした。図からも次元が増えることでターゲットのエリアが疎な状態になり、乱数値がターゲットエリアにヒットしていないことが確認できます。
　この結果より、次元が増えると目標のデータを抽出するためにはより多くのサンプリングが必要となることが直感的に理解できます。

[IN]
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.stats import multivariate_normal
import os
import imageio
import glob

np.random.seed(123) # 乱数の固定

#多変量ガウス分布の描画
mean = np.array([0, 0, 0]) # 平均ベクトルを3次元に
cov = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]]) # 共分散行列を3次元に
target_dist = multivariate_normal(mean, cov) # 多変量ガウス分布の定義

# Set up the proposal distribution
x_max, y_max = 5, 5
x_min, y_min, z_min = -5, -5, 0

# Number of samples
N = 1000
X = np.linspace(x_min, x_max, 100)
Y = np.linspace(y_min, y_max, 100)
X, Y = np.meshgrid(X, Y)
Z = multivariate_normal.pdf(np.dstack((X, Y)), mean=mean[:2], cov=cov[:2, :2])

x_samples = np.random.uniform(x_min, x_max, N) #Xの範囲：-5~5
y_samples = np.random.uniform(y_min, y_max, N) #Yの範囲：-5~5
z_samples = np.random.uniform(z_min, Z.max(), N) #Zの範囲：0~Zの最大値
print(f'形状　x:{x_samples.shape}, y:{y_samples.shape}, z:{z_samples.shape}')

# Perform rejection sampling
samples = []

for i in range(N):
    sample = np.array([x_samples[i], y_samples[i], z_samples[i]])
    if np.random.uniform(0, 1) < target_dist.pdf(sample):
        print(f'目標分布に入ったサンプルIndex：{i}')
        samples.append(sample)
    if i % 10 == 0:  # only plot every 10th sample for efficiency
        fig = plt.figure(figsize=(8, 8), facecolor='white')
        ax = fig.add_subplot(111, projection='3d')
        ax.plot_surface(X, Y, Z, cmap='jet', alpha=0.5)
        ax.scatter(x_samples[:i], y_samples[:i], z_samples[:i], color='blue', alpha=0.1)
        ax.set(xlabel='x', ylabel='y', zlabel='z')
        plt.savefig(f'images/sample_{i:04d}.png')
        plt.close(fig)

samples = np.array(samples)

# Create a GIF animation from the saved images
image_files = glob.glob('images/*.png')
images = [imageio.imread(image_file) for image_file in image_files]
imageio.mimsave('images/rejection_sampling.gif', images)

# Remove the saved images
for image_file in image_files:
    os.remove(image_file)

print(f'Acceptance rate: {len(samples) / N * 100:.1f}%')

[OUT]
形状　x:(1000,), y:(1000,), z:(1000,)
目標分布に入ったサンプルIndex：117
目標分布に入ったサンプルIndex：309
目標分布に入ったサンプルIndex：750
目標分布に入ったサンプルIndex：761
目標分布に入ったサンプルIndex：918
Acceptance rate: 0.5%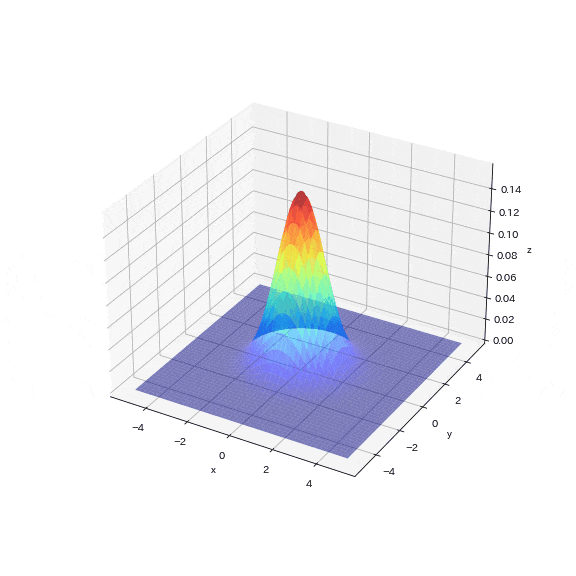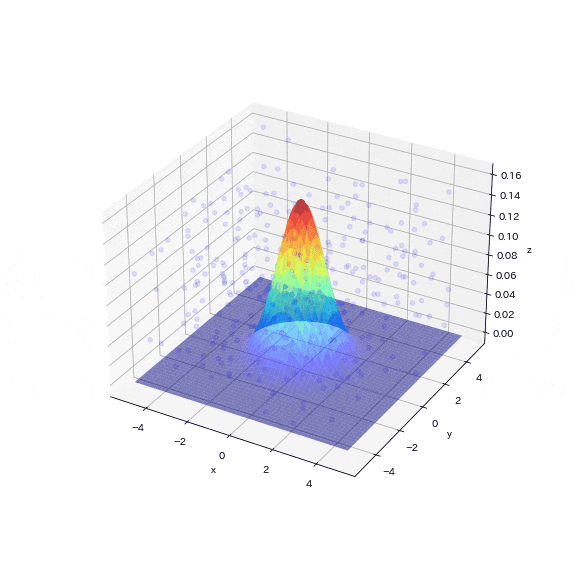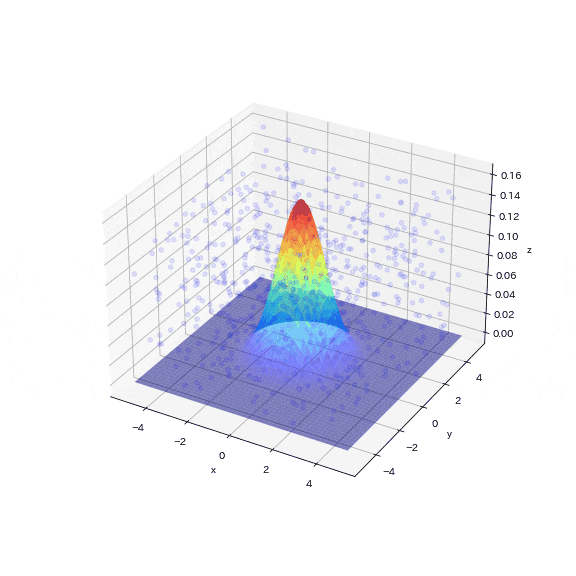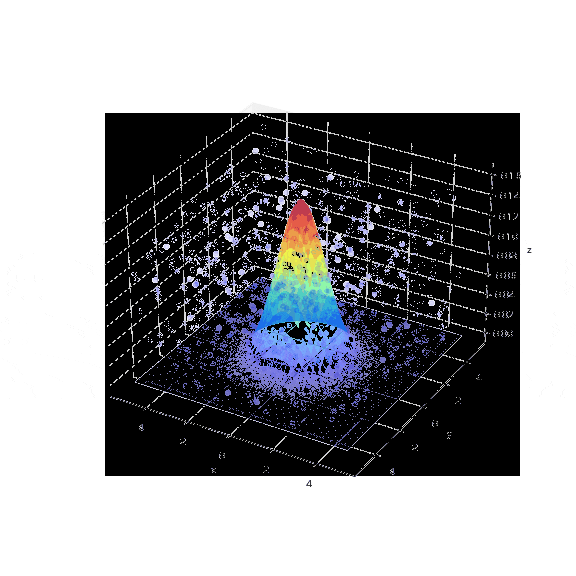

６－２．円周率の計算

　多次元における棄却サンプリングを用いた円周率の計算について考えてみます。多次元の単位球の体積を求める公式を用いて円周率を求めることができ、公式は次の通りです。

$$
V_{N}(r) = \frac{\pi^{N/2}}{\Gamma(\frac{N}{2} + 1)}r^{N}
$$

$$
超格子の体積 = 2^N
$$

$$
d = \sqrt{x_1^2 + x_2^2 + \ldots + x_n^2}
$$

• $${N}$$：次元数

• $${r}$$：半径

• $${V_{N}(r)}$$：$${N}$$次元球の体積

• $${\Gamma}$$：ガンマ関数

• $${2^N}$$：超格子の体積（$${N}$$次元球に接する面同士の空間の体積）

• $${d}$$：サンプリング点の距離（ユークリッド距離）

　見やすいように７次元未満は実線、７次元以上は破線としました。次元が高くなるほど同じサンプリング数でも理論値からのズレが大きくなります。これは高次元になると単位球内に点が落ちる確率が低くなり、結果として多くのサンプリングが必要となることを示しています。これが次元の呪いと呼ばれる現象の一例です。

[IN]
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gamma

def volume_of_sphere(dim, r=1):
    return (np.pi**(dim/2) * r**dim) / gamma(dim/2 + 1) #球の体積の公式（半径r=1）

def monte_carlo_estimate(dim, num_samples):
    """
    モンテカルロ法を用いて、単位球の体積を推定する関数。
    dimは球の次元数、num_samplesはサンプリング数。
    """
    count = 0
    for _ in range(num_samples):
        point = np.random.uniform(-1, 1, dim) #-1~1の一様分布:dim次元
        if np.sum(point**2) <= 1:  # 点が単位球内にある場合
            count += 1
    return 2**dim * count / num_samples  # [-1,1]^dimの立方体の体積は2^dimなので、それに比率を掛ける

dims = range(2, 11)  # 次元数の範囲
num_samples = [10**i for i in range(1, 4)]  # サンプリング数

fig, ax = plt.subplots(1,1 ,figsize=(10, 8), facecolor='white')

for dim in dims:
    true_volume = volume_of_sphere(dim)
    print(f'{dim}次元球の体積: {true_volume:.2f}')
    ratios = []
    for samples in num_samples:
        estimated_volume = monte_carlo_estimate(dim, samples)
        ratio = estimated_volume / true_volume
        ratios.append(ratio)
    
    if dim >= 7:
        ls = '--'
    else:
        ls = '-'
    ax.plot(num_samples, ratios, label=f'dim={dim}', ls=ls)


ax.set(xlabel='サンプル数', ylabel='推定した体積 / 真の体積', xticks=np.arange(0, 1100, 100))
ax.legend(), ax.grid()
plt.show()

[OUT]
2次元球の体積: 3.14
3次元球の体積: 4.19
4次元球の体積: 4.93
5次元球の体積: 5.26
6次元球の体積: 5.17
7次元球の体積: 4.72
8次元球の体積: 4.06
9次元球の体積: 3.30
10次元球の体積: 2.55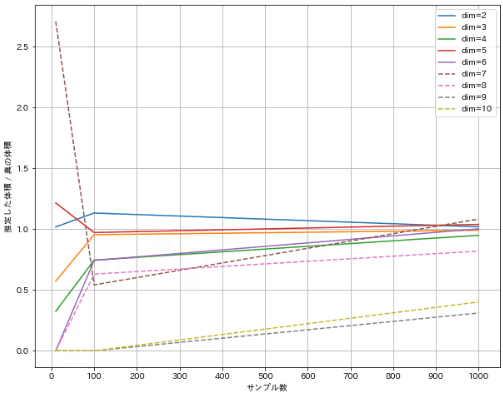

７．マルコフ連鎖モンテカルロ法(MCMC)

　MCMCは計算上扱いにくい確率分布（特に高次元）からのサンプリングを可能にする手法であり、特に対象となる確率分布が高次元で解析的に扱えない場合や、正規化定数が不明な場合などに有用です。（出典：MCMC チュートリアル 入門から多峰性分布の扱いとその応用まで）。
　利用例としてベイジアン統計学における事後分布のサンプリング、統計物理における平衡状態のシミュレーションなどがあります。

７－１．MCMCの手法

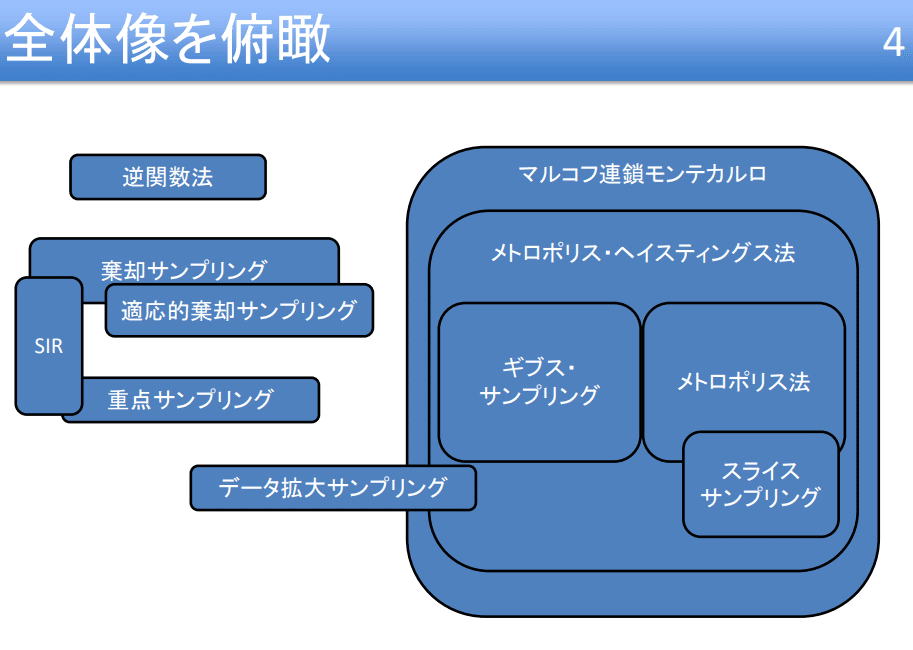
　MCMCの方法はいくつか種類があり、それぞれが異なる提案分布や受容基準を持ちます。以下によく用いられるMCMCの方法をいくつか紹介します。それぞれの手法には特性や利点・欠点があり、具体的な問題に応じて適切な手法を選択することが重要となります。

• メトロポリス・ヘイスティングス法（MH法）： 提案分布が対称であることを仮定して、新しい状態の受容基準を目標分布の確率密度の比率で決定します。この手法は最も基本的なMCMCの手法の一つで、他の多くの手法の基盤となっています。

• ギブスサンプリング：全ての変数を同時に更新するのではなく、1つの変数を条件付き分布からサンプリングして逐次的に更新します。この方法は、目標分布が多次元であっても各変数の条件付き分布が容易にサンプリング可能な場合に特に有用です。

• ハミルトニアンモンテカルロ法（HMC）:：: 物理学の概念を利用し、粒子の運動の模倣を通じて新しい状態を提案します。これにより、高次元の複雑な分布からの効率的なサンプリングが可能となります。ただし、この手法は計算時間が長いという欠点も持っています。

http://bin.t.u-tokyo.ac.jp/summercamp2015/document/prml11_chika.pdf

７－２．MCMCの関連用語

　MCMCに関連する用語を紹介します。

　７－２－１．トレースプロット／バーンイン

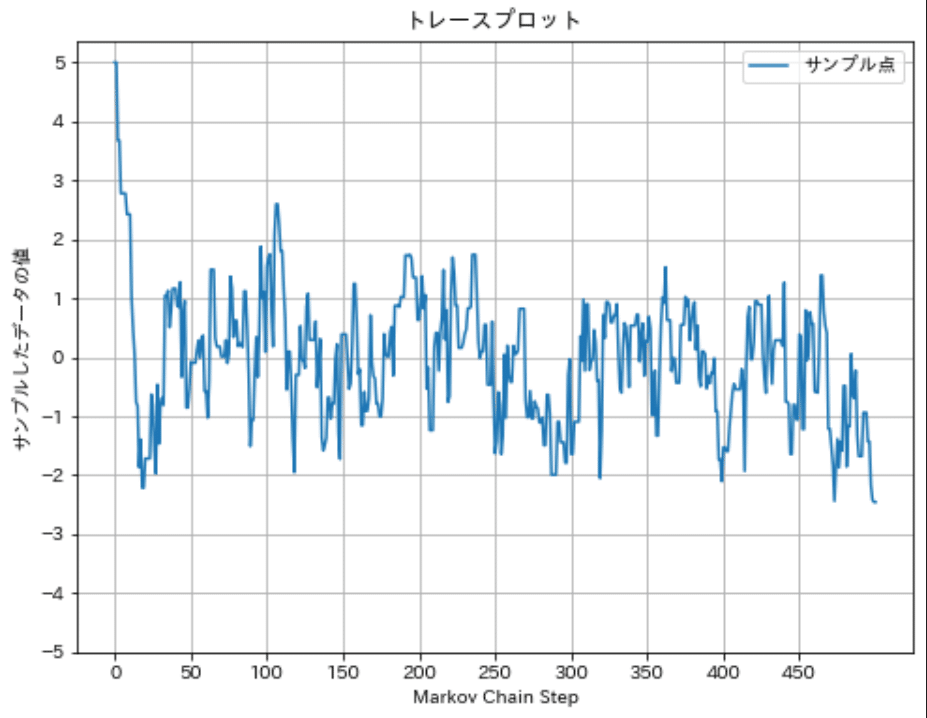
　トレースプロットとはMCMCのプロセスを可視化する手法であり、サンプリングの各ステップで得られた値を順番にプロットしたものです。

　バーンインとはMCMCの初期のステップを結果から除外するプロセスです。MCMCはランダムな初期値からスタートするため、その初期値が理想的な確率分布から遠い場合があります。バーンインは、サンプリングが適切な分布に「収束」するのに十分な時間を与え、初期の偏ったサンプルを無視するために行われます。

　下図は標準正規分布($${\mu=0}$$, $${\sigma^2=1}$$)からサンプリングしたトレースプロットの例です。下図では初期値が5であり確率分布から大きく外れているため、初期のサンプリングを除外する方がより良いサンプリング結果が得られます。

　７－２－２．Gelman-Rubin診断統計量／PSRF値

　Potential scale reduction factor (PSRF)値は、MCMCが適切に収束しているかを確認するための指標です。具体的には、複数のMCMCサンプリングを独立に行い、それぞれのサンプリング間での分散と各サンプリング内での分散を比較します。理想的にはこれらの分散は同じになるはずなので、PSRFが1に近いほどMCMCのサンプリングは収束していると言えます。
　計算式は下記の通りです。

$$
\bar{\theta}_{\cdot j} = \frac{1}{n} \sum_{i=1}^{n} \theta_{ij} \\
\bar{\theta}_{\cdot \cdot} = \frac{1}{m} \sum_{j=1}^{m} \bar{\theta}_{\cdot j}
$$

分散

$$
s_{j}^{2} = \frac{1}{n-1} \sum_{i=1}^{n} (\theta_{ij} - \bar{\theta}_{\cdot j})^{2}\\
$$

Between-chain variance

$$
B = \frac{n}{m-1} \sum_{j=1}^{m} (\bar{\theta}_{\cdot j} - \bar{\theta}_{\cdot \cdot})^{2}
$$

Within-chain variance

$$
W = \frac{1}{m} \sum_{j=1}^{m} s_{j}^{2}=\frac{1}{m(n-1)} \sum_{j=1}^{m} \sum_{i=1}^{n} (\theta_{ij} - \bar{\theta}_{\cdot j})^{2}
$$

Potential scale reduction factor (PSRF)値

$$
\hat{R} = \sqrt{\frac{\hat V}{W}}= \sqrt{\frac{(n - 1)/n + B/nW}{W}}
$$

８．メトロポリス・ヘイスティングス法

　メトロポリス・ヘイスティングス法（MH法）は、一般的なマルコフ連鎖モンテカルロ（MCMC）法の一つです。この手法は特定の確率分布からのサンプリングを目指す問題設定で広く利用されています。

Metropolis–Hastings algorithm - Wikipedia

　MH法は、提案分布と呼ばれる特定の確率分布から新しい状態を提案し、その状態を受け入れるかどうかを確率的に決定します。

８－１．MH法のアルゴリズム

　MH法のアルゴリズムは以下のステップで構成されます。

1. 初期状態$${x}$$を選択

2. 提案分布$${q(x'|x)}$$から新しい状態$${x'}$$を生成する

   • $${q(x'|x)}$$：現在の状態$${x}$$から新しい状態$${x′}$$への遷移を表す確率分布

3. 受入確率（Acceptance Probability）$${r}$$を計算

   • $${r = min(1, \frac{p(x')q(x|x')}{p(x)q(x'|x)})}$$

   • $${r}$$は新しい状態$${x′}$$を受け入れるかを決定するための基準

   • $${p(x)}$$：目標とする確率分布

   • $${q(x'|x)}$$：現在の状態$${x}$$から新しい状態$${x'}$$への提案分布

4. 一様乱数$${u}$$（0から1の範囲）を生成し、もし$${u < r}$$ならば新しい状態$${x'}$$を受け入れ、そうでなければ現在の状態$${x}$$を維持

   • 次の状態は、前の状態に依存せず、現在の状態のみに依存しておりマルコフ性がある。

5. ステップ2～4を指定回数だけ繰り返す

８－２．詳細釣り合いと受入確率r

　詳細釣り合い条件は、あるマルコフ連鎖が定常分布に収束するための重要な要件で、受入確率$${r}$$はこの詳細釣り合い条件を満たすよう設計されています。この条件は「現在の状態から次の状態への遷移」と「その逆遷移の確率」が等しいことを示しています。つまり全ての可能な状態のペア $${x}$$ と $${x'}$$ について以下の等式が成り立つべきです。

$$
P(x'|x)π(x) = P(x|x')π(x')
$$

• $${π(x)}$$：状態$${x}$$の定常確率（状態$${x}$$になる確率）

• $${P(x'|x)}$$：状態$${x}$$から状態$${x'}$$に遷移する確率

　理想的な遷移確率$${P(x|x')}$$（確率密度分布）を見つけるのは難しいため、サンプリングが簡単な提案分布$${q(x|x')}$$に置き換えます。
　しかし、この提案分布を用いた遷移は一般的に詳細釣り合い条件を満たさないため、補正項として受入確率 r が導入されます。これにより、詳細釣り合い条件が満たされるように補正されます。

$$
P(x'|x)π(x) = P(x|x')π(x') \rightarrow rp(x')q(x|x')=p(x)q(x'|x)
$$

$$
r=\frac{p(x')q(x|x')}{p(x)q(x'|x)}=\frac{新しい状態の受入れ度}{現在の状態の保持度}
$$

　前節の式は$${min()}$$を使用しており、$${r\geqq1}$$なら新しい状態をいけ入れ、$${r <1}$$ならこの比率と同じ確率で受け入れます。

$$
r = min(1, \frac{p(x')q(x|x')}{p(x)q(x'|x)})
$$

８－３．MH法の実装／可視化

　MH法をアルゴリズムに従って実装しました。詳細は下記の通りです。

1. 初期状態$${x}$$を選択：stat_init引数に指定

   • 通常は乱数値で決定

   • 本コードでは動作確認やバーンイン紹介のため外れ値を設定

2. 提案分布$${q(x'|x)}$$から新しい状態$${x'}$$を生成する

   • $${q(x'|x)}$$は"propose_distribution"関数化しており正規分布を選択

   • 平均(分布の中心)=現在値, 標準偏差=1.0を$${q(x'|x)}$$として使用

3. 受入確率$${r}$$を計算

   • $${r = min(1, \frac{p(x')q(x|x')}{p(x)q(x'|x)})}$$

   • min(1, a)は1とaの低い方を選択：最大値は1となり、それ以外は右辺の項を選択

   • $${p(x)}$$：目標とする確率分布

   • $${q(x|x')}$$：平均：新しい状態$${x'}$$、 標準偏差=1.0の正規分布における現在値$${x}$$での確率密度

   • $${q(x'|x)}$$：平均：現在値$${x}$$、 標準偏差=1.0の正規分布における新しい状態$${x'}$$での確率密度

4. 一様乱数$${u}$$（0から1の範囲）を生成し、もし$${u < r}$$ならば新しい状態$${x'}$$を受け入れ、そうでなければ現在の状態$${x}$$を維持

5. ステップ2～4を指定回数だけ繰り返す

[IN]
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import numpy as np
from scipy import stats
from typing import Callable, List, Tuple, Union, Optional

def metropolis_hastings(dist_Target, dist_Propose, stat_init, iterations):    
    state = stat_init # 初期状態を設定
    #データ格納リスト ：可視化のためrとuも格納
    samples = [state] #サンプリングデータを格納 （初期値を追加)
    r_values = [0] # 受入確率rを格納するリスト※適当な初期値:0を追加(サンプリング数と同じ長さになる)
    u_values = [0] # 乱数uを格納するリスト※適当な初期値:0を追加(サンプリング数と同じ長さになる)
    
    # サンプリング
    for _ in range(iterations):
        # 提案分布から新しい状態を生成
        state_next = dist_Propose(state, 1) # 平均=state, 標準偏差=1の正規分布からサンプリング
        
        # 受入確率rを計算
        r = min(1, 
            (dist_Target(state_next) * stats.norm.pdf(state, loc=state_next, scale=1)) /
            (dist_Target(state) * stats.norm.pdf(state_next, loc=state, scale=1))
        )
        
        # 一様乱数を生成
        u = np.random.uniform(0, 1) #0 ~1の一様乱数を生成
        
        # 受入確率と比較して新しい状態を受け入れるか判断
        if u < r:
            state = state_next #新しい状態を受け入れ 
        
        #データを格納 
        samples.append(state)
        r_values.append(r) 
        u_values.append(u)
    
    return np.array(samples), r_values, u_values

# 提案分布を生成する関数
def propose_distribution(current: float, scale: float) -> float:
    return np.random.normal(loc=current, scale=scale)

# 目標分布
dist_Target = stats.norm(0, 1).pdf 


samples, r_values, u_values = metropolis_hastings(dist_Target=stats.norm.pdf,
                                            dist_Propose=propose_distribution,
                                            stat_init=5, 
                                            iterations=500)

print(f'サンプル数：{len(samples)}, r数：{len(r_values)}, u数：{len(u_values)}')

fig, ax = plt.subplots(figsize=(8, 6), facecolor="white")
ax.plot(samples, label="サンプル点")
ax.set(xlabel='Markov Chain Step', ylabel='サンプルしたデータの値', title='トレースプロット', 
       xticks=np.arange(0, 500, 50), yticks=np.arange(-5, 6, 1))
ax.grid(), ax.legend()
plt.show()

sns.histplot(samples, kde=True, stat='density')

[OUT]
サンプル数：501, r数：501, u数：501

　初期値を外れ値として5で設定してサンプリングした結果、比較的正規分布に近い分布が得られました。しかしShapiro-Wilk検定で確認するとp<0.05のため正規分布とは言えません。原因はトレースプロットでも確認できるようにサンプリングの初期で分布の外れ値の部分を多くサンプリングしており、そのデータが分布に影響を与えています。
　そこでバーンインとして初期データを全体の20%除外してShapiro-Wilk検定を実施するとp≧0.05で正規分布であることが確認できました。つまり初期データを除外することでより良い分布を取得できました。

[IN]
w, p = stats.shapiro(samples) #正規性の検定 
print(f'W値：{w}, p値：{p}')

w, p = stats.shapiro(samples[100:]) #正規性の検定 
print(f'W値：{w}, p値：{p}')

[OUT]
W値：0.9471960067749023, p値：2.241283330803312e-12
W値：0.9951180219650269, p値：0.2392043173313141

８－４．MH法の可視化による更なる理解

　アルゴリズムをできる限り可視化してみました。可視化のポイントは下記の通りです。

• 目標分布と提案分布の違いを表示

  • 目標分布はサンプリングしたいデータのため不動

  • 提案分布は状態に応じて変わるため変動

• 移動距離は提案分布で用いた分布（分散）に依存するため一定ではない

  • 移動距離も分散で変化する。なお分散の値は適切に設定しないと受入れ率が低くなりサンプリング効率が低下します。

  • 勾配降下法のように一方向への移動ではなく、分布のため正の方向も負の方向にも移動しうる

• 受入確率rは一様乱数(0~1の乱数値)と比較することで、確率的に密度が高い方向へ移動

[IN]
# プロットの初期化
fig, ax = plt.subplots(figsize=(10, 8), facecolor="white")
x = np.linspace(-10, 10, 1000) # x軸の値
ax.plot(x, dist_Target(x), label="目標分布", color='blue')
samples_line, = ax.plot([], [], 'o', color='gray', label='サンプリングデータ')
current_state_line, = ax.plot([], [], 'o', color='red', label='現在の状態')
proposal_line, = ax.plot([], [], '--', color='gray', label='提案分布(正規分布)')
acceptance_text = ax.text(0.06, 0.5, '', transform=ax.transAxes, fontsize=17)
ax.grid(True)
ax.legend(loc='upper right')

# アニメーションの更新関数
def update(i):
    current_state = samples[i]
    if i > 0:
        previous_state = samples[i-1]
    else:
        previous_state = current_state
    
    # 過去のサンプリングデータはy=0にプロット
    samples_line.set_data(samples[:i+1], [0]*len(samples[:i+1]))
    
    # 現在の状態は目標分布の上にプロット
    current_state_line.set_data(current_state, dist_Target(current_state))
    
    # 新しい提案分布を描画
    proposal_line.set_data(x, stats.norm.pdf(x, loc=current_state, scale=1))
    
    acceptance_text.set_text('Iteration: {}\nCurrent state: {:.2f}\nAccepted: {}\nr値: {:.2f}\nu(乱数): {:.2f}'.format(i, current_state, current_state != previous_state, r_values[i], u_values[i]))
    return samples_line, current_state_line, proposal_line, acceptance_text

# アニメーションの生成※10回に1回の割合で更新
ani = FuncAnimation(fig, update, frames=range(0, len(samples), 5), blit=True)

# GIFとして保存
ani.save('metropolis_hastings.gif', writer='pillow', fps=100)

[OUT]

＃＃＃＃＃＃修正中※おそらく間違いあり＃＃＃＃＃＃＃＃＃＃＃＃＃

９．ギブスサンプリング

　ギブスサンプリングとは「多次元分布に対して、全体の確率分布を各次元の「条件付き分布」に分解し、それぞれの条件付き分布から交互にサンプリングする手法」です。
　これにより多次元分布でもサンプリングが可能となります。

９－１．MH法の課題とギブスサンプリングの特徴

　MH法では提案分布を用いてサンプリングの乱数を作成しました。１次元では提案分布を選択しやすいですが多次元だと最適な分布の選定が難しく、提案分布の選択が適切でないと高次元の問題で非効率的なります。この問題を解決する手法としてギブスサンプリングがあります。

　ギブスサンプリングは一度に一つの変数だけを考慮するため、多次元の問題を一次元の問題に「分解」できます。分解手法としてはその変数の条件付き確率分布を使用します。

９－２．用語・数式の定義

　今回は二変量ガウス分布からギブスサンプリングを用いてサンプリングしたいと思います。事前に使用する数式を記載しました。

　各種記号は下記の通りです。

• $${x}$$と$${y}$$：2次元正規分布の2つの変数(サンプリングする変数)

• $${\mu_x}$$と$${\mu_y}$$：$${x}$$と$${y}$$の平均値

• $${\bf \mu}$$：平均値ベクトル（2次元正規分布の中心）

• $${\sigma_x^2}$$と$${\sigma_y^2}$$：$${x}$$と$${y}$$の分散

• $${\Sigma}$$：分散共分散行列（2次元正規分布の形状）

• $${\rho}$$：$${x}$$と$${y}$$の間の相関係数を示します

• $${N()}$$：正規分布の表記

• $${p(x, y)}$$：$${x}$$と$${y}$$の同時分布

• $${p(x | y)}$$：$${y}$$が与えられたときの$${x}$$の条件付き分布

• $${p(y | x)}$$：$${x}$$が与えられたときの$${y}$$の条件付き分布

　９－２－１．二変量ガウス分布の数式

【2次元正規分布（同時分布）：二変量ガウス分布】

$$
p(x, y) \sim N\left( \mathbf{\mu}, \mathbf{\Sigma} \right)
=N\left( [\mu_x, \mu_y], \begin{bmatrix} \sigma_x^2 & \rho\sigma_x\sigma_y \\ \rho\sigma_x\sigma_y & \sigma_y^2 \end{bmatrix} \right)
$$

【二変量ガウス分布における各次元（変数）の条件付き分布】
　これらの条件付き分布の形は一般的な正規分布の形と同じです。下記式よりy固定におけるxの正規分布において平均：$${\mu_x + \rho\sigma_x (\frac{y - \mu_y}{\sigma_y})}$$、分散：$${\sigma_x^2(1 - \rho^2)}$$となります。

$$
p(x | y) \sim N\left(\mu_x + \rho\sigma_x\left(\frac{y - \mu_y}{\sigma_y}\right), \sigma_x^2\left(1 - \rho^2\right)\right)
$$

$$
p(y | x) \sim N\left(\mu_y + \rho\sigma_y\left(\frac{x - \mu_x}{\sigma_x}\right), \sigma_y^2\left(1 - \rho^2\right)\right)
$$

【分散共分散行列$${\Sigma}$$の特徴】
　別記事で紹介の通り分散共分散行列$${\Sigma}$$の特徴の１つとして　「行列の対角成分は各次元（各データ）における分散」があります。

$$
\Sigma
= \begin{bmatrix} \sigma_{x}^2 & \text{Cov}(x, y) \\ \text{Cov} (y, x)& \sigma_{y}^2 \end{bmatrix}= \begin{bmatrix} \sigma_x^2 & \rho\sigma_x\sigma_y \\ \rho\sigma_x\sigma_y & \sigma_y^2 \end{bmatrix}
= \begin{bmatrix} xの分散 & x・yの共分散 \\ y・xの共分散 & yの分散 \end{bmatrix}
$$

　９－２－２．多変量ガウス分布の数式

　多次元正規分布の密度関数は次のようになります。

$$
f(x) = \frac{1}{\sqrt{(2\pi)^n|\Sigma|}} \exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)
$$

　これを$${x_j}$$：現在サンプリングを行っている次元と$${x_{-j}}$$：既にサンプリングされた変数の値に分けると下記の条件付き分布が得られます。

$$
f(x_j | x_i) =\mathcal{N}(\mu_{j|i}, \sigma_{j|i}^2)
= \frac{1}{\sqrt{2\pi\sigma_{j|i}^2}} \exp\left(-\frac{(x_j-\mu_{j|i})^2}{2\sigma_{j|i}^2}\right)
$$

$$
\mu_{j|i} = \mu_j + \frac{\Sigma_{k=1}^{j-1} (x_{k} - \mu_{k})}{\sigma_{j, j}}
$$

$$
\sigma_{j|i}^2 = \sigma_{j,j}
$$

９－３．ギブスサンプリングのアルゴリズム

　ギブスサンプリングのアルゴリズムは以下のステップで構成されます。

1. 初期のサンプル点（状態）$${x}$$をランダムに選択

2. 1つの次元を固定し、それが既知であると仮定して他の次元の条件付き分布からサンプリング

   • この条件付き確率分布は、他の全ての変数が既知であるときのその変数の確率分布

   • あくまでサンプリング済みの次元の値を用いてサンプリングしており、まだサンプリングしていない次元の条件付き分布ではない

   • 多次元分布$${(x_{1}, x_{2}, \cdots, x_{j}, \cdots, x_{n})}$$があり、$${j}$$次元をサンプリングする時$${x_{1}, x_{2}, \cdots, x_{j-1}}$$までは既知だが$${x_{j+1}}$$以降は未知となる。

3. 次に新たにサンプリングされた値を固定し、それが既知であると仮定して元の次元の条件付き分布からサンプリング

4. これらのステップを交互に繰り返すことで、全体の分布からのサンプルを生成

　ギブスサンプリングの特徴として下記があります。

【メリット】

• 各次元の条件付き分布からのサンプリングは比較的簡単なため、全体の分布が複雑でも計算可能

• 高次元の分布に対しても適用可能（例：大規模なデータセットに対する分析など）

• 正規化定数（全確率の和を1にするための定数）が無くてもサンプリングが可能

【デメリット】　

• 「各変数の条件付き分布が容易に計算できる」という条件が必要です。これが満たされない場合ギブスサンプリングは実装が難しくなります。

• サンプリングはランダムのため良い近似値を得るために多数のサンプルを必要とします。このため収束速度が遅いという特性があります。

• 変数間の依存性が高いと効率が悪くなることがあります。これは１つの変数が他の多くの変数に強く影響を受ける場合、サンプリングの収束に時間がかかることを意味します。

【参考】

【Python】4.3.2：ポアソン混合モデルにおける推論：ギブスサンプリング【緑ベイズ入門のノート】 - からっぽのしょこ

わかりやすいギブスサンプリング - Yosshi Labo.

ギブスサンプリング - Wikipedia

http://watanabe-www.math.dis.titech.ac.jp/~kohashi/document/bayes_51.pdf

９－４．ギブスサンプリングの実装

　９－４－１．実装コードの動作確認（3次元)

　コードを確認するためのサンプル目標分布は平均ベクトル$${\bf \mu}$$,分散共分散行列 $${\bf \Sigma}$$が下記の3次元ガウス分布からギブスサンプリングでサンプリングしてみます。
　なお分布の原点は$${\mu}$$ですが、サンプリング開始点は[0, 0, 0]としています。

$$
\bf \mu = \begin{bmatrix}\mu_1 \\ \mu_2 \\ \mu_3\end{bmatrix}
= \begin{bmatrix}1 \\ 2 \\ 3\end{bmatrix}
$$

$$
\Sigma
= \begin{bmatrix}\sigma_{xx} & \sigma_{xy} & \sigma_{xz}\\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz}\end{bmatrix} = \begin{bmatrix}1 & 0.5 & 0.3 \\ 0.5 & 2 & 0.2 \\ 0.3 & 0.2 & 3\end{bmatrix}
$$

　まずはコード実装および出力を記載しました。

[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import seaborn as sns
import japanize_matplotlib
import scipy.stats as stats
from IPython.display import display, Math, Latex


np.set_printoptions(precision=3, suppress=True) #有効桁数3桁 、指数表示しない

def gibbs_sampling(mu, sigma, iterations: int, seed:int=123):
    if seed:
        np.random.seed(seed) # 乱数の固定
        
    ndim_mu = mu.shape[0] #平均ベクトルの次元数 
    samples = np.zeros((iterations, ndim_mu)) #サンプリング ×次元数の行列->各行にサンプリングデータを格納

    print(f'サンプリング開始点={samples[0]}') 
    display(Latex(r'$\sigma_x={:.3f}$'.format(sigma[0, 0]))) #Σからxの分散を表示
    display(Latex(r'$\sigma_y={:.3f}$'.format(sigma[1, 1]))) #Σからyの分散を表示
    display(Latex(r'$\sigma_z={:.3f}$'.format(sigma[2, 2]))) #Σからzの分散を表示
    
    for i in range(iterations):
        for j in range(ndim_mu): #各次元についてサンプリング 
            print(f'{"#"*10}イテレーション:{i}, {j+1}次元:{"#"*10}')
            if j > 0:
                mu_j = mu[j] + np.dot(sigma[j, :j], (samples[i, :j] - mu[:j])) / sigma[j, j]
                print(f'sigma[j, :j]={sigma[j, :j]}')
                print(f'samples[i, :j]={samples[i, :j]}')
                print(f'mu[:j]={mu[:j]}')
            else:
                mu_j = mu[j]

            sigma_j = sigma[j, j] #j番目の次元の条件付き分散 
            display(Latex(r'条件付き平均$\mu_j$:{:.3f}, 条件付き分散$\sigma_j$:{:.3f}'.format(mu_j, sigma_j)))
            
            #正規分布N (j次元の平均, j次元の条件付き分散)からサンプリング
            samples[i, j] = np.random.normal(mu_j, np.sqrt(sigma_j))
            print(f'samples:\n{samples}')
    
    return samples


# パラメータ設定
mu = np.array([1.0, 2.0, 3.0]) # 平均ベクトル
sigma = np.array([[1.0, 0.5, 0.3], 
                  [0.5, 2.0, 0.2],
                  [0.3, 0.2, 3.0]]) # 共分散行列

# ギブスサンプリング実行
samples = gibbs_sampling(mu=mu, 
                         sigma=sigma,
                         iterations=3, 
                         seed=123)
samples

[OUT]
途中経過

[OUT:最終出力のみ] 
array([[-0.086,  3.139,  3.458],
       [-0.506,  0.805,  5.63 ],
       [-1.427,  0.787,  4.869]])

【解説】

　初めの次元$${x}$$のサンプリングは既知情報が無いため平均値、すなわち分布の中心は目標分布（ここでは3次元ガウス分布）の平均ベクトル$${\bf  \mu}$$から$${\mu_1=1.0}$$値をそのまま使用します。1次元目の分散は$${ \Sigma_{11}=\sigma_{xx}=1.0}$$を使用することで下記正規分布が得られるため、ここからランダムサンプリングできます。結果として"-0.086"が得られました。

$$
f(x)=\dfrac{1}{\sqrt{2\pi\sigma_{xx}^2}}\exp(-\dfrac{(x-\mu_1)^ 2}{2\sigma_{xx}^ 2})
=\dfrac{1}{\sqrt{2\pi}}\exp(-\dfrac{(x-1.0)^ 2}{2})
$$

　次の次元$${y}$$のサンプリング では$${\mu_2=2.0}$$ではなく条件付き平均$${\mu_j' = \mu_j + \frac{\sum_{k=1}^{j-1}\sigma_{jk}(x_k - \mu_k)}{\sigma_{jj}}}$$を使用します。計算式は下記の通りです。

$$
\mu_j' = \mu_2 + \frac{\sigma_{yx}\times(x_{サンプル値}-\mu_1)}{\sigma_{yy}}
=2+\frac{0.5\times(-0.086-1.0)}{2.0}=1.729
$$

　ここで得られた 条件付き平均$${\mu_j'}$$と条件付き分散$${\sigma_{yy}}$$の正規分布からサンプリングします。結果として"3.139"が得られました。

 最後の次元では今まで得られた次元$${x}$$、$${y}$$の平均、分散、サンプリング値を用いて$${z}$$の条件付き平均を求めていきます。結果として"3.458"が得られました。

$$
\mu_j' = \mu_3 + \frac{\sigma_{zx}\times(x_{サンプル値}-\mu_1)+\sigma_{zy}\times(y_{サンプル値}-\mu_2)}{\sigma_{zz}}
=3+\frac{0.3\times(-0.086-1.0)+0.2\times(3.139-2.0)}{3.0}=3.458
$$

　９－４－２．実装（2次元)

９－５．ギブスサンプリングの可視化

追って

１０．ハミルトニアンモンテカルロ法

追って

１０－１．アルゴリズム：HM法

---

---

参考記事

あとがき 

　そろそろガウス過程回帰書きたい・・・・・