Pythonで学ぶ統計学５：推測統計（検定）

2023年1月6日 23:10

１．概要

　本記事は統計学の学習記録用として作成しており、私が理解するのに時間がかかった場所や追って参照したい内容を中心にまとめております。
　本記事のテーマは「推測統計：（仮説）検定」になります。

　参考資料として下記（CC-BY）を使用させていただきました。

１－１．記事説明：データとPythonライブラリ

　本記事で使用したサンプルデータを紹介します。本題ではないため詳細な説明は省きます。
　またPythonも使用していきますがライブラリの詳細説明は省きますので個別のライブラリは別記事で確認お願いします。なおScipyは(2023年1月現在)では記事を作成しておりませんがこちらも説明は省きます。

２．用語の説明

２－１．用語一覧

　検定に関する用語は多数あるため本章で一覧を記載しました。

母数：母平均や母分散など、母集団が持つ固有の統計量のこと
検定統計量：仮設検定において統計量と比較するための指標であり「統計量z（z値）：標準化されたデータ」や「統計量t（t値）」があります。
検定(test)：データである「標本」をもとにして検定統計量を計算し、「母集団」に関する各種の仮説に関する適否の判断を行うもの（ピアソンにより定式化された）
帰無仮説$${H_{0}}$$（null hypothesis）：棄却（否定）されることを目的に立てられる仮説のこと（差なし仮説ともいう）。
対立仮説$${H_{1}}$$（alternative hypothesis）：統計的仮説検定において、帰無仮説が棄却されたときに採択される仮説のこと。（差あり仮説ともいう）
有意確率（p値）：p値とは標本の結果（標本平均など）が、帰無仮説が正しい場合に発生する確率（可能性）である。つまりp値が基準値(優位水準α)より小さいと”発生確率(p値)が低い->帰無仮説はほとんどあり得ない”として「有意差あり」と判断される。
p値の補足1：有意水準5%とは仮説が正しい場合にこの手順を多数回実施して検定を行うとき、間違って帰無仮説を棄却する割合が5%であるという意味であり、特定の判断が間違っている確率が5%ということではない。
有意水準・棄却域α：検定において帰無仮説を設定したときにその帰無仮説を棄却する基準となる確率
αの補足１：統計的仮説検定において第一種の過誤を犯す確率のことで、P値の小ささの基準である
αの補足２：一般的には5%や1 %が使用されますが、研究・品質目的での許容されるエラーに合わせて個々に設定します。
検出力：有意水準と対するものとして、「検出力」があります。検出力は1-βで表される。βは「第2種の過誤の確率」を表す。
信頼区間：ー
両側検定・片側検定：ー
自由度：ー
２標本検定：2つの独立した母集団があり、各母集団から抽出した標本の平均に差があるかどうかを検定することを「2標本t検定」という。
F検定：２つの母集団から抽出した標本（F値=2標本の母分散の比）を使用して、２つの母集団が同じかどうか推定する手法（等分散か判断する）
Z検定：標準正規分布を使用した検定
t検定：t分布を使用した検定であり、独立した２群間における母平均の差の検定
p検定：ー
多重検定：ー
分散分析（ANOVA)：分散ではなく母平均に差があるか確認
第1種の過誤：帰無仮説が正しいのに棄却する
第2種の過誤：帰無仮説が正しいのに採択する
パラメトリック検定：検定に用いる統計量（Z値、t値、F値など）が特定の分布に従うと仮定を置く検定方法
ノンパラメトリック検定：検定に用いる統計量の分布に特別な分布型を仮定しない検定方法->標本数が小さい場合や標本の分布が不明の場合に使用する。ただし検定力はパラメトリック検定に比べて低くなる

２－２．用語の数式・計算式

　各種統計量の数式は下記の通りです。

$$
統計量t（Welchのt検定） = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}} \cdot \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}
$$

$${\bar{x}_1}$$, $${\bar{x}_2}$$：2つの群のサンプル平均、$${s_1^2}$$, $${s_2^2}$$：2つの群の不偏分散、$${n_1}$$, $${n_2}$$：2つの群のサンプルサイズ

２－３．コラム：p値の誤解

　p値とは「特定の統計モデルの元でデータの統計的要約（例：２グループ比較での標本平均の差）が観察された値と等しいか、より極端な値をとる確率」ですが、誤解が多い指標とのことです。
　P値の原則は下記の６つがあるとのことです。結論は「P値を計算したら終わりではなく、必要に応じて追加の検証も実施する必要がある」です。

原則１：P 値はデータと特定の統計モデルが矛盾する程度をしめす指標のひとつである
原則２：P 値は、調べている仮説が正しい確率や、データが偶然のみでえられた確率を測るものではない。
原則３：科学的な結論や、ビジネス、政策における決定は、P値がある値（訳注: 有意水準）を超えたかどうかにのみ基づくべきではない。
原則４：適正な推測のためには、すべてを報告する透明性が必要である。
原則５：P 値や統計的有意性は、効果の大きさや結果の重要性を意味しない。：「統計的に優位」と「科学的に意味がある」ことは同義ではない。
原則６：P 値はそれだけでは統計モデルや仮説に関するエビデンスの、よい指標とはならない。

（出典：日本計量生物学会　統計的有意性とP値に関するASA声明）
（出典：Youtube　京都大学大学院医学研究科聴講コース臨床研究者のための生物統計学「仮説検定とP値の誤解」佐藤俊哉医学研究科教授）

３．推測統計の検定とは

３－１．推定と検定の違い

　推測統計は大きく分けて「推定問題」と「検定問題」があります。本記事では検定を紹介しますが「基本的な考え方・計算する統計量は検定・推定とも同じ」です。大まかにいうと、推定：母集団の母数を算出、検定：母集団の母数が仮説にあうか判定　します。

●推定：母集団の特性値（平均や分散など）を標本のデータから統計学的に推測することであり、推定には点推定と区間推定がある。
●検定：母集団に関して、ある仮説が統計学的に成り立つか否かを、標本のデータを用いて判断すること

３－２．検定の手順

　検定には手順があり、流れは下記の通りです。

仮説の設定：帰無仮説$${H_{0}}$$と対立仮説$${H_{1}}$$を立てる
検定法の選定：分析目的に合った検定方法（検定手法や片側・両側など）を分析者が選定する
有意水準α・棄却域の決定：有意水準αの決定(一般的にはα=0.05、厳しいときはα=0.01を選定）
検定統計量と有意点を算出：標本から検定統計量、有意水準に対する有意点を算出
仮説の判定：検定統計量が棄却域内か確認、検定統計量に対するp値、有意水準を比較

（出典：数理統計学まとめ（その 10）：第 6 章検定）

　下記が参考として分かりやすいため紹介します。

http://mdsc.kyushu-u.ac.jp/wp/wp-content/uploads/2021/08/65acc4fde28714c38e918402c2d5c32a.pdf

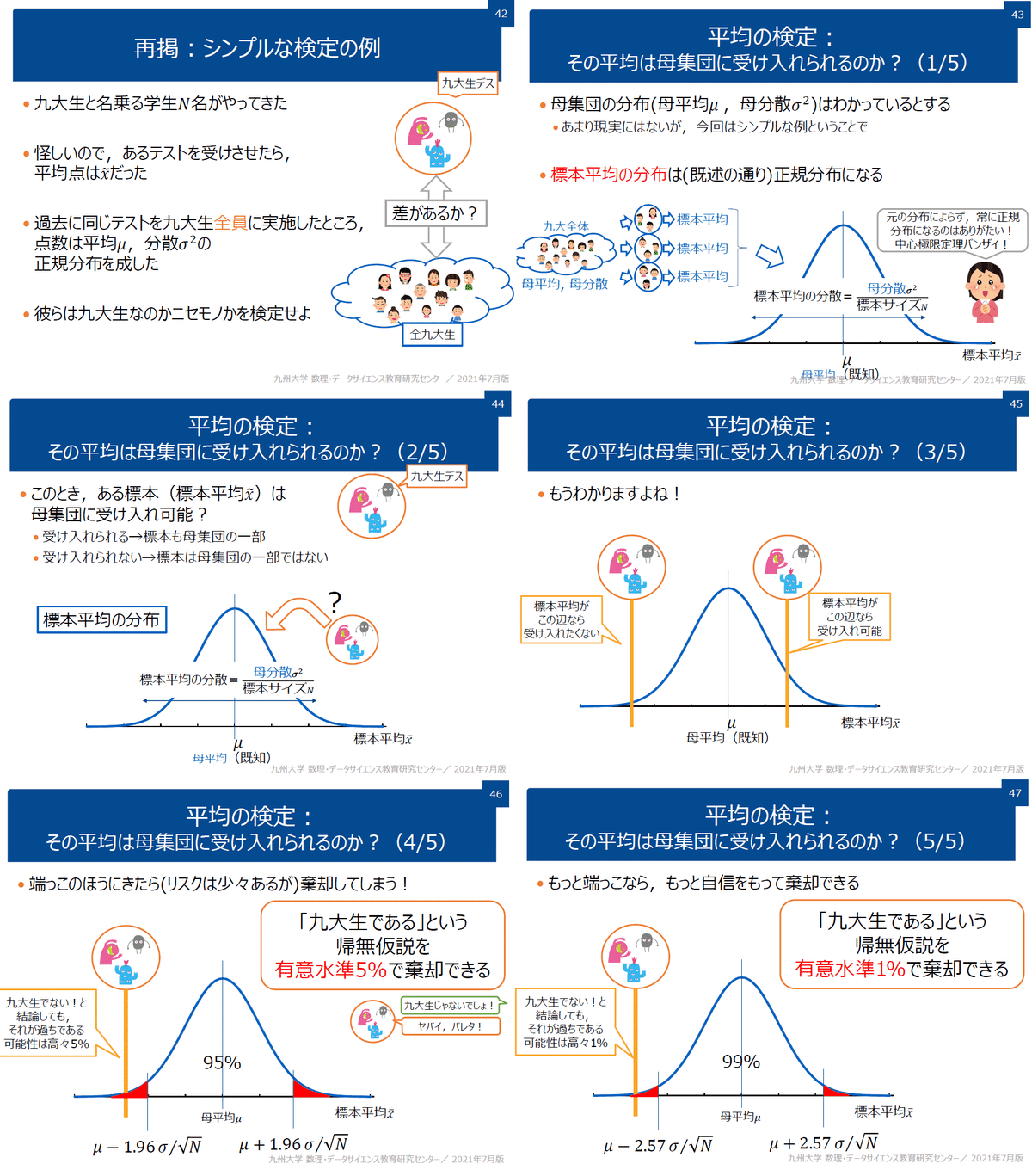
４．検定における重要用語

４－１．帰無仮説と対立仮説

　（推定における母集団の母数（μやσ）の区間を推定とは異なり、）検定では「母集団がある仮説が正しいか（例：母数はXである、２標本は同じなど）」を判定する手法です。そのため検定では確認したい目的に合わせて仮説を設定します。
　検定を行うため立てる仮説のことを「帰無仮説」、帰無仮説に対する仮説のことを「対立仮説」といいます。

【帰無仮説$${H_{0}}$$（null hypothesis）】
　一般的には「証明したいものとは逆の仮説」となる。帰無仮説を棄却（帰無仮説$${H_{0}}$$が間違っている）することで対立仮説$${H_{1}}$$が正しい（主張は正しい）というロジックとする。
　帰無仮説$${H_{0}}$$の正しさは$${H_{0}}$$が起こりえる確率p値を設定して、確率的に起こりにくい場合は棄却する。棄却するか否かの基準値を優位水準αと言い、「p<αなら帰無仮説を棄却」する。

【対立仮説$${H_{1}}$$（alternative hypothesis）】
　一般的には「証明したい仮説」となる。

　仮説検定では「いったん主張したいこと（対立仮説$${H_{1}}$$）とは逆の仮説（帰無仮説$${H_{0}}$$）を立て、それを否定することで主張を通す」ため背理法と似たロジックとなります。

【コラム：逆に対立仮説を棄却するとどうなるの？】
　結論としては対立仮説を棄却しても帰無仮説は主張できません。これは帰無仮説と対立仮説には非対称性があり、「帰無仮説を棄却->対立仮説が正しい」を主張できても、その逆は真とはならないためです。　

【背理法とは】
１．ある事柄を証明するのに、まずその事柄が成り立たないと仮定して矛盾を導き、それによって事柄の成り立つことを証明する方法
２．証明すべき結論を否定して論理を進めていき、与えられた条件と対立する結論を導き出して矛盾（不合理）を示す一つの証明法である。

４－２．両側検定と片側検定

　検定には「両側検定」と「片側検定」がありますが、考え方は推定で紹介した内容で理解できます。
　確率分布（正規分布やt分布）にはある区間での確率は決まっております。下図は標準正規分布ですが、確率：68.3%, 95.4%, 99.7%となるときの区間を左右対称（両側）と片方（片側）でプロットしました。結果として同じ確率でも片側の方が（片方のみですが）区間が広くなっています（p=68.3％では、両側は1以上だと棄却されますが、片側だと0.48で棄却されます）。
　よって「片側検定の方が有利になりやすい（両側検定の方が厳しく$${H_{0}}$$が棄却されにくい）」特徴があります。

　両側検定と片側検定の使い分けは目的に応じて決定され、例としては下記のようなものがあります。

【両側検定】
　標本間の大小に関係なく、差があるかどうかを確認したい場合
（例：成分の物性差、効果の有無確認）

【片側検定】
　標本間の大小（単純な差だけではなく有意差を確認）を確認したい場合
（例：新薬の性能）

[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy import stats
import glob
import os


x = np.linspace(-4, 4, 100)
y = stats.norm.pdf(x, 0, 1)
#標準正規分布の確率：両側検定
sigma = 1
p_1sigma = stats.norm.cdf(sigma*1)-stats.norm.cdf(-sigma*1) #-σ～σの確率
p_2sigma = stats.norm.cdf(sigma*2)-stats.norm.cdf(-sigma*2) #-2σ～2σの確率
p_3sigma = stats.norm.cdf(sigma*3)-stats.norm.cdf(-sigma*3) #-3σ～3σの確率
print(f'-σ～σの確率：{p_1sigma:.3f}, -2σ～2σの確率：{p_2sigma:.3f}, -3σ～3σの確率：{p_3sigma:.3f}')
#片側検定
x_side1 = stats.norm.ppf(0.683, 0, 1) #p_sigma(-σ～σでの確率)と同じ
x_side2 = stats.norm.ppf(0.954, 0, 1) #p_sigma(-2σ～2σでの確率)と同じ
x_side3 = stats.norm.ppf(0.997, 0, 1) #p_sigma(-3σ～3σでの確率)と同じ


fig, axs = plt.subplots(1, 2, figsize=(14, 6), facecolor='w')
#両側検定
axs[0].plot(x, y, label='標準正規分布')
axs[0].fill_between(x, y, where=(x>=-1*sigma)&(x<=1*sigma), color='red', alpha=0.2, label=f'-σ～σの確率：{p_1sigma:.3f}')
axs[0].fill_between(x, y, where=(x>=-2*sigma)&(x<=2*sigma), color='orangered', alpha=0.2, label=f'-2σ～2σの確率：{p_2sigma:.3f}')
axs[0].fill_between(x, y, where=(x>=-3*sigma)&(x<=3*sigma), color='orange', alpha=0.2, label=f'-3σ～3σの確率：{p_3sigma:.3f}')
axs[0].text(sigma, 0.3, 'σ', fontsize=12, color='red')
axs[0].text(-1*sigma*1.1, 0.3, '-σ', fontsize=12, color='red')
axs[0].text(2*sigma, 0.1, '2σ', fontsize=12, color='orangered')
axs[0].text(-2*sigma*1.1, 0.1, '-2σ', fontsize=12, color='orangered')
axs[0].text(3*sigma, 0.05, '3σ', fontsize=12, color='orange')
axs[0].text(-3*sigma*1.05, 0.05, '-3σ', fontsize=12, color='orange')
axs[0].annotate('', xy=(sigma, 0.25), xytext=(sigma, 0.3), arrowprops=dict(arrowstyle='->', color='red'))
axs[0].annotate('', xy=(-sigma, 0.25), xytext=(-sigma, 0.3), arrowprops=dict(arrowstyle='->', color='red'))
axs[0].annotate('', xy=(2*sigma, 0.06), xytext=(2*sigma, 0.1), arrowprops=dict(arrowstyle='->', color='orangered'))
axs[0].annotate('', xy=(-2*sigma, 0.06), xytext=(-2*sigma, 0.1), arrowprops=dict(arrowstyle='->', color='orangered'))
axs[0].annotate('', xy=(3*sigma, 0.01), xytext=(3*sigma, 0.05), arrowprops=dict(arrowstyle='->', color='orange'))
axs[0].annotate('', xy=(-3*sigma, 0.01), xytext=(-3*sigma, 0.05), arrowprops=dict(arrowstyle='->', color='orange'))
axs[0].legend(loc='upper right'), axs[0].grid()

#片側検定
axs[1].plot(x, y, label='標準正規分布')
axs[1].fill_between(x, y, where=(x>=x_side1), color='red', alpha=0.2, label=f'片側:{p_1sigma*100:.1f}%')
axs[1].fill_between(x, y, where=(x>=x_side2), color='orangered', alpha=0.5, label=f'片側:{p_2sigma*100:.1f}%')
axs[1].fill_between(x, y, where=(x>=x_side3), color='blue', alpha=1, label=f'片側:{p_3sigma*100:.1f}%')
axs[1].text(x_side1, 0.35, f'x={x_side1:.2f}', fontsize=12, color='red')
axs[1].text(x_side2, 0.1, f'x={x_side2:.2f}', fontsize=12, color='orangered')
axs[1].text(x_side3, 0.02, f'x={x_side3:.2f}', fontsize=12, color='blue')

axs[1].legend(loc='upper right'), axs[1].grid()
plt.suptitle('標準正規分布における片側と両側の確率イメージ', fontsize=14, y=0)
plt.show()

[OUT]
上図

４－３．間違えるリスク：第１種の過誤と第２種の過誤

　検定は「統計的に優位な差が見られた」ことを説明できますが因果関係や母集団の真値などは教えてくれません。よって検定をしても（確率的に）間違えることはあり、間違え方によって２つの過誤があります。

【第１種の過誤α：擬陽性、α過誤、あわてものの誤り】
　帰無仮説が正しいのに帰無仮説を棄却する誤り（差がないのに違いありと判断する）。帰無仮説を棄却する基準値の優位水準αを調整することで第１種の過誤をコントロールできる。

【第２種の過誤β：偽陰性、β過誤、ぼんやりものの誤り】
　対立仮説が正しいのに帰無仮説を棄却しない誤り（差があるのに無いとする）。第２種の過誤を起こす確率はβで表すが、その反対で差を正しいと判断できる確率を検出力（1－β)と言います。

　第１種と第２種の過誤（αとβ）にはトレードオフの関係があり、片方を小さくするともう片方が大きくなります。設定値α・βは何に重きをおくかで基準値が変わります。
　例として、品質に厳しく不良品を出したくない工場であれば第２種の過誤は避けたい（不良品が出荷される）ため、検出力を上げる(つまりβを下げる->αは上がる）ことで見逃しを防止しますが、逆に正常品を不良品と判断（第１種の過誤）する確率が増えるため検査数の増加（つまり工数upによるコストup）が発生します。

５．１標本検定：母数の確率検証

　１標本検定：標本が１個のみであり母集団との比較を実施します。

５－１．母平均の検定

　標本から母集団の平均（母平均）を検定します。条件は下記の通りです。

【シミュレーションの条件】
●内容：最近出費額が増えていると感じている。直近の毎月の出費が真値（母平均）から変動したかどうかを確認したい。
●母平均（真値）$${\mu}$$：120
●標本数n：12 （よって自由度は11）
●優位水準：5%
●確率分布：t分布（母分散：未知、母集団：正規分布、標準偏差：標本の不偏分散から算出※Pandasでは不偏分散となるためそのまま計算）
●検定TYPE：両側検定（出費の変化を確認するため、両側に設定）

$$
t値=\frac{\bar x – μ}{\frac {U}{\sqrt{n}}}
$$

$${\bar x}$$：標本平均、$${\mu}$$：母平均、$${n}$$：標本数、U：標本の不偏分散による標準偏差、$${\frac {U}{\sqrt{n}}}$$：標準誤差、

【検定の手順】
１．仮説の設定：　帰無仮説$${H_{0}：\bar{X}=\mu}$$より、対立仮説$${H_{1}：\bar{X}≠\mu}$$
２．検定法の選定：母分散は未知であり、データ数も大量ではないためt分布に設定
３．有意水準α・棄却域の決定：α=0.05(95%信頼区間)に設定
４．検定統計量と有意点を算出：t値、p値を計算（※p値は両側検定のため、片側を計算して2倍する）
５．仮説の判定：結果として帰無仮説$${H_{0}：\bar{X}=\mu}$$は棄却されなかった。

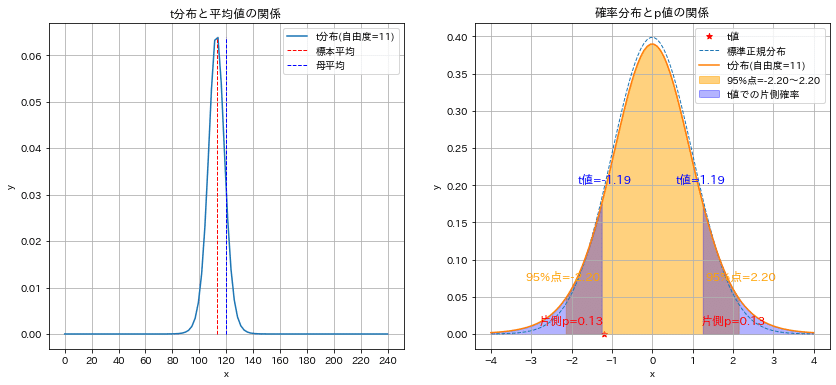
　まず統計量t値を計算するとt値=-1.19となりt分布の95%信頼区間：-2.2~2.2の間にあるため$${H_{0}：\bar{X}=\mu}$$は棄却されない、つまり差があるとは言えないと判断できます（※差が無いと言っているのではなく、統計学的に差があるとは言えないという意味です）。
　またp値を計算すると25.9%であり、帰無仮説が正しい場合に本結果（母集団の分布に対する標本平均）の起こりえる確率が25.9%あるため、帰無仮説は棄却できない（つまり差はない）と判断できます。

[IN]
mean_p = 120 #母平均
#標本
data = np.array([109.0, 152.2, 111.4, 110.6, 127.5, 107.3, 93.3, 92.0, 111.6, 75.7, 128.6, 135.1])
df = pd.DataFrame(data, columns=['Spend'], index=[f'{i}月' for i in range(1, 13)])
display(df.T)

df_stats = df.describe() #統計量の計算
display(df_stats.T)

df_stats = df_stats['Spend']
mean, std, nums_sample = df_stats['mean'], df_stats['std'], df_stats['count'] #平均、標準偏差、サンプル数
d_free = nums_sample - 1 #自由度
stderror = std / np.sqrt(nums_sample) #標準誤差

t_value = (mean - mean_p) / stderror #t値
#両側検定
lim_low_t95 = stats.t.ppf(0.025, d_free) #t分布の95%点(両側検定のため2.5%点)
lim_high_t95 = stats.t.ppf(0.975, d_free) #t分布の95%点(両側検定のため97.5%点)
#p値の計算
p_value = stats.t.cdf(t_value, d_free) * 2 #t分布の累積分布関数（Cumulative Distribution Function）
print(f'両側検定：t値={t_value:.2f}、t分布の95%点={lim_low_t95:.2f}～{lim_high_t95:.2f}, p値={p_value:.3f}')

[OUT]
両側検定：t値=-1.19、t分布の95%点=-2.20～2.20, p値=0.259

　この意味を理解するために各数値をすべて可視化しました。下図から下記が確認できました。

t値とはt分布（確率分布）におけるx軸を計算している。
優位水準αとは信頼区間、つまりt分布（確率分布）における発生確率を決める指標であり$${X%信頼区間=100\times(1-\alpha)}$$である。
p値とは（両側検定では）計算された統計量（t値）の外側の確率、つまり計算したt値から外れる（外側になる）確率を意味する。
p値が小さい=t分布のより外側にある=発生する確率は小さいこと
値は違えど、基本的にt値とp値は同じ指標である

[IN]
#可視化（グラフ１）：t分布と標本の関係
x = np.linspace(0, 240, 100)
y = stats.t.pdf(x, d_free, mean, stderror) #t分布の確率密度関数（Probability Density Function）
fig, axs = plt.subplots(1, 2, figsize=(14, 6), facecolor='w', edgecolor='k')

axs[0].plot(x, y, label=f't分布(自由度={int(d_free)})')
axs[0].vlines(mean, 0, y.max(), color='red', label='標本平均', ls='dashed', lw=1.0)
axs[0].vlines(mean_p, 0, y.max(), color='blue', label='母平均', ls='dashed', lw=1.0)

#可視化（グラフ２）：#t分布の95%点の区間を塗りつぶし
x_std = np.linspace(-4, 4, 100)
t_stddist = stats.t.pdf(x_std, d_free) #t分布の確率密度関数（Probability Density Function）
stdnorm_dist = stats.norm.pdf(x_std) #標準正規分布の確率密度関数（Probability Density Function）
axs[1].scatter(t_value, 0, color='red', marker='*', label=f't値')
axs[1].plot(x_std, stdnorm_dist, label='標準正規分布', ls='dashed', lw=1.0)
axs[1].plot(x_std, t_stddist, label=f't分布(自由度={int(d_free)})')
axs[1].fill_between(x_std, t_stddist, where=(x_std>=lim_low_t95)&(x_std<=lim_high_t95), color='orange', alpha=0.5, label=f'95%点={lim_low_t95:.2f}～{lim_high_t95:.2f}')
axs[1].fill_between(x_std, t_stddist, where=(x_std<=t_value), color='blue', alpha=0.3, label=f't値での片側確率')
axs[1].fill_between(x_std, t_stddist, where=(x_std>=-t_value), color='blue', alpha=0.3)

#アノテーション追加
axs[1].text(t_value, 0.20, f't値={t_value:.2f}', ha='center', va='bottom', color='blue', fontsize=12)
axs[1].text(-t_value, 0.20, f't値={-t_value:.2f}', ha='center', va='bottom', color='blue', fontsize=12)
axs[1].text(lim_low_t95, 0.07, f'95%点={lim_low_t95:.2f}', ha='center', va='bottom', color='orange', fontsize=12)
axs[1].text(lim_high_t95, 0.07, f'95%点={lim_high_t95:.2f}', ha='center', va='bottom', color='orange', fontsize=12)
axs[1].text(-2, 0.01, f'片側p={p_value/2:.2f}', ha='center', va='bottom', color='red', fontsize=12)
axs[1].text(2, 0.01, f'片側p={p_value/2:.2f}', ha='center', va='bottom', color='red', fontsize=12)

#体裁調整
axs[0].set(xlabel='x', ylabel='y', xticks=np.arange(0, 260, 20), title='t分布と平均値の関係')
axs[0].legend(loc='upper right'), axs[0].grid()

axs[1].set(xlabel='x', ylabel='y', title='確率分布とp値の関係')
axs[1].legend(loc='upper right'), axs[1].grid()
plt.show()

[OUT]
上図

５－２．母比率の検定

　標本から母比率を検定します。条件は下記の通りです。

【シミュレーションの条件】
●内容：アンケートで政党Aの指示を確認し、前回調査から支持率が上昇したか確認したい。
●母比率（真値）$${p}$$：0.75 (前回アンケート結果)
●標本数n：2000人
●優位水準：5%
●確率分布：標準正規分布（母集団：ベルヌーイ分布と仮定）
●検定TYPE：片側検定（上昇の有無を確認するため片側に設定）

$$
z値=\frac{R-p}{\sqrt{\frac{p(1-p)}{n}}}
$$

$${R}$$：標本比率、$${p}$$：母比率、$${n}$$：標本数、$${\sqrt{\frac{p(1-p)}{n}}}$$：標準誤差

【検定の手順】
１．仮説の設定：　帰無仮説$${H_{0}：R<x}$$より、対立仮説$${H_{1}：R>=x}$$
２．検定法の選定：比率のためベルヌーイ分布に設定
３．有意水準α・棄却域の決定：α=0.05(95%信頼区間)に設定
４．検定統計量と有意点を算出：z値、p値を計算（※p値は片側検定のため1倍のまま）
５．仮説の判定：結果として帰無仮説$${H_{0}：\bar{X}=\mu}$$は棄却されるため増加したと判断

　計算結果より下記が確認できました。

z値は標準正規分布の片側95%区間より外側にいるため、普段は起こりえない事象が起こっていると判断できる（有意差がある）
z値からp値を計算するとp=0.02(2%)であり”帰無仮説が正しい場合の発生確率が低い”ため帰無仮説を棄却できます。
帰無仮説の棄却より「有意差あり」と判断できるため、「標本比率は母比率より増加した」と判断できる。

[IN]
ratio_p = 0.75 #母比率
#標本
nums_sample = 2000
nums_True = 1540
ratio_s = nums_True / nums_sample #標本比率

def calc_zvalue(R, p, n):
    '''
	p: 母比率, R: 標本比率, n: 標本数
 	'''
    z = (R - p) / np.sqrt(p * (1 - p) / n) #
    return z

z_value = calc_zvalue(ratio_s, ratio_p, nums_sample)
p_value = stats.norm.sf(z_value) #標準正規分布の累積分布関数（Cumulative Distribution Function）の逆関数（PPF: Percent Point Function）
print(f'母比率p:{ratio_p}, 標本比率R:{ratio_s}, 標本数n:{nums_sample}, z値:{z_value:.2f}, p値:{p_value:.3f}')

#標準正規分布
x = np.linspace(-4, 4, 100)
stdnorm = stats.norm.pdf(x) #標準正規分布の確率密度関数（Probability Density Function）
lim95_1side = stats.norm.ppf(0.95) #標準正規分布の95%点（1側）(PPF: Percent Point Function)

#可視化
fig = plt.figure(figsize=(8, 6), facecolor='w', edgecolor='k')
plt.plot(x, stdnorm, label='標準正規分布')
plt.scatter(z_value, 0, color='red', marker='*', label=f'z値={z_value:.2f}')
plt.fill_between(x, stdnorm, where=(x<=lim95_1side), 
                 color='blue', alpha=0.3, label=f'片側95%区間={lim95_1side:.2f}')
plt.fill_between(x, stdnorm, where=(x>=z_value),
                 color='red', alpha=0.2, label=f'z値での片側確率')

plt.legend(loc='upper right'), plt.grid()
plt.show()
plt.show()

[OUT]
母比率p:0.75, 標本比率R:0.77, 標本数n:2000, z値:2.07, p値:0.019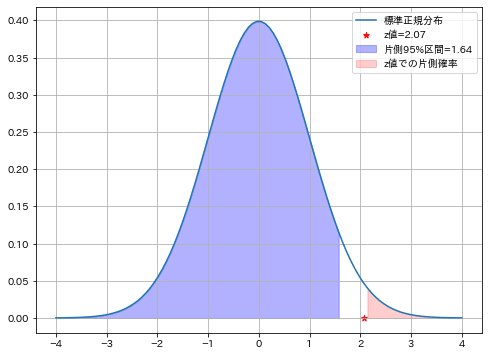

５－３．母分散の検定

　標本から母分散（ばらつき）を検定します。条件は下記の通りです。

【シミュレーションの条件】
●内容：工場において使用する材料を変更したところ、ばらつきが増えた気がする。本当にばらつきが増加したか確認したい。
●母分散（真値）$${\sigma^2}$$：0.01 (材料変更前の分散)
●標本数n：10
●優位水準：5%
●確率分布：$${\chi^2}$$分布（母集団：正規分布と仮定）
●検定TYPE：両側検定（変化があるかを確認するため）

$$
t値=\frac{(n-1)U^2}{\sigma^2}
$$

$${U^2}$$：標本の不偏分散、$${\sigma^2}$$：母分散、$${n}$$：標本数

【検定の手順】
１．仮説の設定：　帰無仮説$${H_{0}：U^2≠\sigma^2}$$より、対立仮説$${H_{1}：U^2=\sigma^2}$$
２．検定法の選定：母分散を推定するため$${χ^2}$$分布を選定
３．有意水準α・棄却域の決定：α=0.05(95%信頼区間)に設定
４．検定統計量と有意点を算出：t値、p値を計算
５．仮説の判定：結果として帰無仮説$${H_{0}：\bar{X}=\mu}$$は棄却されず変化があるとは認められない

　計算結果より下記が確認できました。

計算したt値は$${χ^2}$$分布の95%区間内に入っており、確率的にはあり得ることが分かる。
p値を計算（t値以上となる確率）すると16.3%と優位水準αより高く、良く生じる事象と判断でき帰無仮説を棄却できない。
結果として有意差があるとは判断できない。

[IN]
#母分散
var_p = 0.01 

#標本データ
data = np.array([6.28, 6.33, 6.52, 6.44, 6.31, 6.40, 6.49, 6.68, 6.34, 6.44])
nums_sample = len(data) #標本数
var_unbiased = data.var(ddof=1) #不偏分散
d_free = nums_sample - 1 #自由度

t_value = (nums_sample-1) * var_unbiased/var_p
print(f'母分散:{var_p}, 標本分散:{var_unbiased:.4f}, 自由度:{d_free}, t値:{t_value:.2f}')

#Chi2分布
x=np.linspace(0, 30, 100)
y_chi2 = stats.chi2.pdf(x, d_free) #Chi2分布の確率密度関数（Probability Density Function）
lim_low_chi95 = stats.chi2.ppf(0.025, d_free) #Chi2分布の95%点（下側）(PPF: Percent Point Function)
lim_high_chi95 = stats.chi2.ppf(0.975, d_free) #Chi2分布の95%点（上側）(PPF: Percent Point Function)
p_value = stats.chi2.sf(t_value, d_free) #Chi2分布の累積分布関数（Cumulative Distribution Function）の逆関数（PPF: Percent Point Function）
print(f'Chi2分布の95%点（下側）:{lim_low_chi95:.2f}, Chi2分布の95%点（上側）:{lim_high_chi95:.2f}, p値:{p_value:.3f}')

#可視化
fig = plt.figure(figsize=(8, 6), facecolor='w', edgecolor='k')
plt.plot(x, y_chi2, label='χ2分布')
plt.scatter(t_value, 0, color='red', marker='*', label=f't値')
plt.fill_between(x, y_chi2, where=(x<=lim_low_chi95), 
                 color='orange', alpha=0.3, label=f'両側95%区間:下限')
plt.fill_between(x, y_chi2, where=(x>=lim_high_chi95),
                 color='blue', alpha=0.9, label=f'両側95%区間:上限')
plt.fill_between(x, y_chi2, where=(x>=t_value),
                 color='red', alpha=0.2, label=f'p値')

plt.annotate(f't値={t_value:.2f}', xy=(t_value, 0.002), xytext=(t_value, 0.01), arrowprops=dict(facecolor='red', shrink=0.01))
plt.annotate(f'下限={lim_low_chi95:.2f}', xy=(lim_low_chi95, 0.002), xytext=(lim_low_chi95, 0.01), arrowprops=dict(facecolor='orange', shrink=0.01))
plt.annotate(f'上限={lim_high_chi95:.2f}', xy=(lim_high_chi95, 0.002), xytext=(lim_high_chi95, 0.01), arrowprops=dict(facecolor='blue', shrink=0.01))

plt.xlabel('t値'), plt.ylabel('確率密度')
plt.title(f'Fig. 自由度:{d_free}のχ2分布とt値の関係', y=-0.15)
plt.legend(loc='upper right'), plt.grid()
plt.show()


[OUT]
母分散:0.01, 標本分散:0.0144, 自由度:9, t値:12.98
Chi2分布の95%点（下側）:2.70, Chi2分布の95%点（上側）:19.02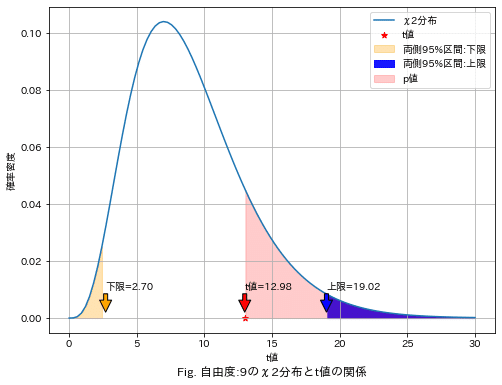

６．２標本検定：母集団の比較

２標本検定では２つの標本を比較し、それらの母集団（の母数）に差があるか確認します。

６－１．母平均の差の検定

　標本1と標本2の母平均の差を考えます。

　正規分布同士の差は正規分布に従うため、今までと同様に検定できます。なお標本の差をとった場合平均値は引き算だが、ばらつきは足し算になることに注意が必要です。

$$
標本1　\bar{X}=\mathcal{N}(\mu_{1}, \frac{\sigma_{1}^2}{m}),
$$

$$
標本２　\bar{Y}=\mathcal{N}(\mu_{2}, \frac{\sigma_{2}^2}{n})
$$

$$
標本平均の差=\bar{X}-\bar{Y}=\mathcal{N}(\mu_{1}-\mu_{2}, \frac{\sigma_{1}^2}{m}+\frac{\sigma_{2}^2}{n})
$$

$$
Z=\frac{\bar{X}-U}{\frac{\sigma}{\sqrt{n}}}　より2標本では
$$

$$
Z=\frac{\bar{X}と\bar{Y}との群間差}{標本のばらつき}=\frac{\bar{X}-\bar{Y}-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^2}{m}+\frac{\sigma_{2}^2}{n}}}
$$

【標本１】
$${\bar{X}}$$：標本平均、$${\mu_{1}}$$：母平均、$${\sigma_{1}}$$：標準偏差、m：データ数
【標本２】
$${\bar{Y}}$$：標本群、$${\mu_{2}}$$：母平均、$${\sigma_{2}}$$：標準偏差、n：データ数

　統計量ｚ値は母分散が既知と未知の時で考えることができます。

　６－１ー１．等分散と仮定：Z検定

　標本１・２の分散が同じ（等分散）であれば分散は同じ値に集約できるので前述の統計量を下記の通り変更できます。

$$
Z=\frac{\bar{X}-\bar{Y}-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^2}{m}+\frac{\sigma_{2}^2}{n}}}=\frac{\bar{X}-\bar{Y}-(\mu_{1}-\mu_{2})}{\sqrt{(\frac{1}{m}+\frac{1}{n})\sigma^2}}
$$

　母分散は未知のため同じ母分散を持つ２つの標本を合算して、２つの不偏分散から合併した分散を作り母分散を推定すると下記式となります。

$$
T=\frac{\bar{X}-\bar{Y}-(\mu_{1}-\mu_{2})}{\sqrt{(\frac{1}{m}+\frac{1}{n})(\frac{(m-1)U_{1}^2+(n-1)U_{2}^2}{m+n+2})}}
$$

$${U_1}$$：標本の標準偏差、$${U_2}$$：標本の標準偏差

　サンプルとしてテストの点数を比較すると考えます。帰無仮説で標本1と標本2の平均値は同じと仮定すると$${\mu_{1}-\mu_{2}=0}$$となるため統計量Tを計算することが可能となります。

標本１：$${\bar{X_{2}}}$$=63、$${\mu_{1}}$$=None、$${\sigma_{1}}$$=5、m=40
標本２：$${\bar{X_{2}}}$$=58、$${\mu_{2}}$$=None、$${\sigma_{2}}$$=10、m=60

　統計量Tはt分布（自由度：m+n-2）に従うため、いつも通りの区間推定ができます。今回は信頼区間から外れているため帰無仮説が棄却され、有意差がある（標本１の結果の方が優れている）と言えます。

[IN]
#標本1
X1 = 63 #標本平均
var1 = 5**2 #標本分散
num1 = 40 #標本数
#標本2
X2 = 58 #標本平均
var2 = 10**2 #標本分散
num2 = 60 #標本数

d_free = num1 + num2 - 2 #自由度

#2標本のt検定
def calc_tvalue_2sample(X1, var1, num1, X2, var2, num2):
    diff_U = 0 #母平均の差は同じと仮定
    var_pool = ((num1-1)*var1 + (num2-1)*var2) / (num1+num2-2)
    t = (X1-X2-diff_U) / np.sqrt(var_pool*(1/num1 + 1/num2))
    return t

t_value = calc_tvalue_2sample(X1, var1, num1, X2, var2, num2)
print(f't値:{t_value:.2f}')


#t分布
x_std = np.linspace(-4, 4, 100)
t_stddist = stats.t.pdf(x_std, d_free) #t分布の確率密度関数（Probability Density Function）
stdnorm_dist = stats.norm.pdf(x_std) #標準正規分布の確率密度関数（Probability Density Function）
lim_low_t99 = stats.t.ppf(0.005, d_free) #t分布の99%点（下側）(PPF: Percent Point Function)
lim_high_t99 = stats.t.ppf(0.995, d_free) #t分布の99%点（上側）(PPF: Percent Point Function)
print(f't分布の99%点（下側）:{lim_low_t99:.2f}, t分布の99%点（上側）:{lim_high_t99:.2f}')

#可視化
fig = plt.figure(figsize=(8, 6), facecolor='w', edgecolor='k')
plt.scatter(t_value, 0, color='red', marker='*', label=f't値')
plt.plot(x_std, stdnorm_dist, label='標準正規分布', color='lightblue', ls='dashed', lw=1.0)
plt.plot(x_std, t_stddist, label=f't分布(自由度={int(d_free)})', color='blue', lw=1.0)

plt.fill_between(x_std, t_stddist, where=(x_std>=lim_low_t99)&(x_std<=lim_high_t99),
                 color='orange', alpha=0.5, label=f'95%点={lim_low_t99:.2f}～{lim_high_t99:.2f}')

#アノテーション追加
plt.text(lim_high_t99, 0.05, f'99%点:{lim_high_t99:.2f}', ha='center', va='bottom', color='blue', fontsize=12)
plt.text(lim_low_t99, 0.05, f'99%点:{lim_low_t99:.2f}', ha='center', va='bottom', color='blue', fontsize=12)
plt.arrow(lim_high_t99, 0.045, 0.0, -0.02, head_width=0.05, head_length=0.01, fc='blue', ec='blue')
plt.arrow(lim_low_t99, 0.045, 0.0, -0.02, head_width=0.05, head_length=0.01, fc='blue', ec='blue')
plt.text(t_value*1.1, 0.02, f't値:{t_value:.2f}', ha='center', va='bottom', color='red', fontsize=12)


plt.legend(loc='upper right'), plt.grid()
plt.show()

[OUT]
t値:2.92
t分布の99%点（下側）:-2.63, t分布の99%点（上側）:2.63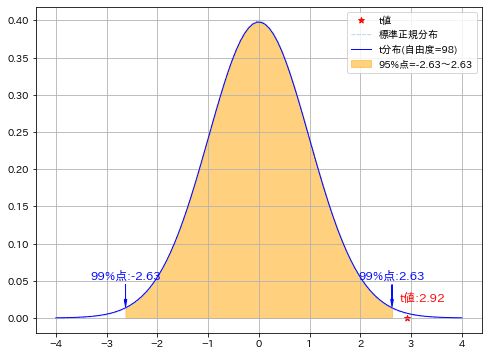

　６－１ー２．等分散出ない場合：ウェルチのt検定

　等分散を仮定しない場合は$${\bar{X}-\bar{Y}}$$の正確な分布は分かりませんが以下の形で近似できます（等分散の時より分母の形がシンプルになっています）。またこの時にt分布が従う自由度はm+n-2ではなく下記式となります。

$$
T=\frac{\bar{X}-\bar{Y}-(\mu_{1}-\mu_{2})}{\sqrt{\frac{U_{1}^2}{m}+\frac{U_{2}^2}{n}}}
$$

$$
自由度ν = \frac{(\frac{U_{1}^2}{m} + \frac{U_{2}^2}{n})^2}{\frac{(\frac{U_{1}^2}{m})^2}{m-1} + \frac{(\frac{U_{2}^2}{n})^2}{n-1}}
$$

　先ほどと標本のデータは同じにして、等分散を仮定せずに計算しました。結果は下記の通りです。

結論は同じであり帰無仮説を棄却して差があることが確認できた。
自由度は98->92に変化したがデータ数が多くほぼ標準正規分布と同じ形になっているため影響はほぼなかった。
t値はより外側に移動した。

[IN]
def calc_dfree(var1, var2, num1, num2):
    numerator = (var1/num1 + var2/num2)**2
    denominator = (var1/num1)**2/(num1-1) + (var2/num2)**2/(num2-1)
    return int(round(numerator/denominator, 0))

def calc_tvalue_welch(X1, var1, num1, X2, var2, num2):
    diff_U = 0 #母平均の差は同じと仮定
    t = (X1-X2-diff_U) / np.sqrt(var1/num1 + var2/num2)
    return t

d_free_calc = calc_dfree(var1, var2, num1, num2)
t_value_welch = calc_tvalue_welch(X1, var1, num1, X2, var2, num2)
print(f'自由度:{d_free_calc}, t値:{t_value_welch:.2f}')


#t分布
x_std = np.linspace(-4, 4, 100)
t_stddist = stats.t.pdf(x_std, d_free_calc) #t分布の確率密度関数（Probability Density Function）
stdnorm_dist = stats.norm.pdf(x_std) #標準正規分布の確率密度関数（Probability Density Function）
lim_low_t99 = stats.t.ppf(0.005, d_free_calc) #t分布の99%点（下側）(PPF: Percent Point Function)
lim_high_t99 = stats.t.ppf(0.995, d_free_calc) #t分布の99%点（上側）(PPF: Percent Point Function)
print(f't分布の99%点（下側）:{lim_low_t99:.2f}, t分布の99%点（上側）:{lim_high_t99:.2f}')

#可視化
fig = plt.figure(figsize=(8, 6), facecolor='w', edgecolor='k')
plt.scatter(t_value_welch, 0, color='red', marker='*', label=f't値')
plt.plot(x_std, stdnorm_dist, label='標準正規分布', color='lightblue', ls='dashed', lw=1.0)
plt.plot(x_std, t_stddist, label=f't分布(自由度={int(d_free_calc)})', color='blue', lw=1.0)

plt.fill_between(x_std, t_stddist, where=(x_std>=lim_low_t99)&(x_std<=lim_high_t99),
                 color='orange', alpha=0.5, label=f'95%点={lim_low_t99:.2f}～{lim_high_t99:.2f}')

#アノテーション追加
plt.text(lim_high_t99, 0.05, f'99%点:{lim_high_t99:.2f}', ha='center', va='bottom', color='blue', fontsize=12)
plt.text(lim_low_t99, 0.05, f'99%点:{lim_low_t99:.2f}', ha='center', va='bottom', color='blue', fontsize=12)
plt.arrow(lim_high_t99, 0.045, 0.0, -0.02, head_width=0.05, head_length=0.01, fc='blue', ec='blue')
plt.arrow(lim_low_t99, 0.045, 0.0, -0.02, head_width=0.05, head_length=0.01, fc='blue', ec='blue')
plt.text(t_value_welch*1.1, 0.02, f't値:{t_value_welch:.2f}', ha='center', va='bottom', color='red', fontsize=12)


plt.legend(loc='upper right'), plt.grid()
plt.show()

[OUT]
自由度:92, t値:3.30
t分布の99%点（下側）:-2.63, t分布の99%点（上側）:2.63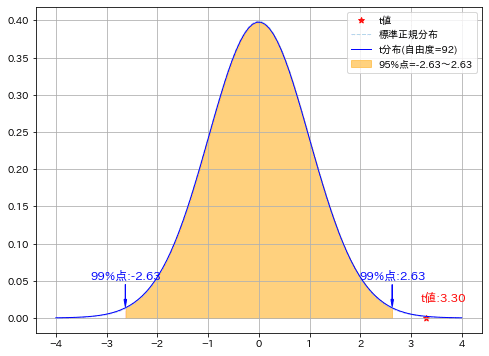

　参考として体重で検定した記事を紹介します。

　６－１ー３．対応（ペア）がある：ペアt検定

　２標本検定において対応（ペア）があるもの、つまり基本的に同じ標本対象で測定した物であれば、２標本間の分布を正規分布とおけば１標本検定と同様に扱えます。
　下記練習問題：被験者５人に対して薬を投与して、その前後で血圧を測定したうえで薬に効果があるか（$${\mu_{1}=\mu_{2}}$$を棄却）を確認します（優位水準5%の片側検定）。

　実施より下記が確認できました。

計算より標本１・２（投薬前後）の差分を1つの標本として取り扱い１標本検定を実施するのと同じ内容になった
差分が標本のため、母平均の差は帰無仮説として$${\mu_{1}-\mu_{2}=0}$$とできる。
確率としてt分布内に存在する。またp値=0.10であり優位水準α=5%より大きいため帰無仮説は棄却されない。つまり有意差がない（血圧は下がっていない）と判断される。

[IN]
data = np.array([[180, 150,  30],
                 [130, 135,  -5],
                 [165, 145,  20],
                 [155, 150,   5],
                 [140, 140,   0]])
df_data = pd.DataFrame(data, columns=['投与前の血圧', '投与後の血圧', '差分'])


#標本間の平均
diff_mu = 0 #帰無仮説H0:標本間の平均は同じと仮定

#標本の統計量
nums_sample = df_data.shape[0]
mean_diff_s = df_data['差分'].mean()
std_diff_s = df_data['差分'].std(ddof=1) #不偏標準偏差
d_free= nums_sample - 1 #自由度

t_value = (mean_diff_s - diff_mu) / (std_diff_s / np.sqrt(nums_sample))
p_value = stats.t.sf(np.abs(t_value), d_free) #t分布の累積分布関数（Cumulative Distribution Function）の逆関数
print(f'標本間の平均の差:{mean_diff_s:.2f}, 標本間の標準偏差:{std_diff_s:.2f}, t値:{t_value:.2f}, p値:{p_value:.2f}')

#t分布
x_std = np.linspace(-4, 4, 100)
t_stddist = stats.t.pdf(x_std, d_free) #t分布の確率密度関数（Probability Density Function）
stdnorm_dist = stats.norm.pdf(x_std) #標準正規分布の確率密度関数（Probability Density Function）
lim_t95_1side = stats.t.ppf(0.95, d_free) #t分布の95%点（上側）(PPF: Percent Point Function)


#可視化
fig = plt.figure(figsize=(8, 6), facecolor='w', edgecolor='k')
plt.scatter(t_value, 0, color='red', marker='*', label=f't値')
plt.plot(x_std, stdnorm_dist, label='標準正規分布', ls='dashed', lw=1.0)
plt.plot(x_std, t_stddist, label=f't分布(自由度={int(d_free)})', color='blue', lw=1.0)
plt.fill_between(x_std, t_stddist, where=(x_std>=lim_t95_1side),
                 color='orange', alpha=0.5, label=f'95%点={lim_t95_1side:.2f}')

#アノテーション追加
plt.text(lim_t95_1side, 0.1, f'95%点:{lim_t95_1side:.2f}', ha='center', va='bottom', color='blue', fontsize=12)
plt.arrow(lim_t95_1side, 0.095, 0.0, -0.02, head_width=0.05, head_length=0.01, fc='blue', ec='blue')
plt.text(t_value*1.1, 0.02, f't値:{t_value:.2f}', ha='center', va='bottom', color='red', fontsize=12)


plt.legend(loc='upper right'), plt.grid()
plt.show()

[OUT]
標本間の平均の差:10.00, 標本間の標準偏差:14.58, t値:1.53, p値:0.10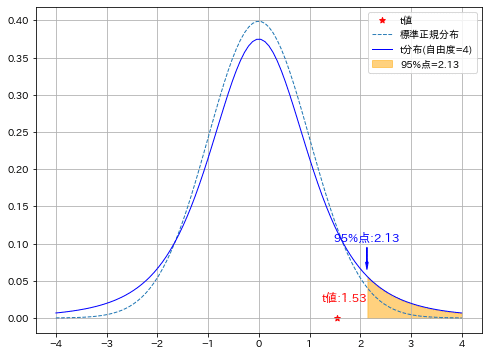

６－２．母比率の差の検定

　６－２－１．ベルヌーイ分布ベース

　標本1と標本2の母比率の差を考えます。ベルヌーイ分布では平均：p、分散：p(1-p)であり帰無仮説$${H_0:p_1=p_2}$$を前提にすると等分散と仮定できるため、下記式が得られます。なお母比率は不明のため、推定値で計算します。

$$
z= \frac{X_1 - X_2-(\mu_{1}-\mu_{2})}{\sqrt{(\frac{1}{m}+\frac{1}{n})\sigma^2}} \to \frac{X_1 - X_2}{\sqrt{\hat{p}(1-\hat{p})(\frac{1}{m} + \frac{1}{n}})}
$$

$$
合併した分散（母比率の推定値）\hat{p}=\frac{mX_1+nX_2}{m+n}
$$

$${X_1 }$$：標本1の標本比率、$${m}$$：標本1の標本数、$${X_2}$$：標本2の標本比率、$${n}$$：標本2の標本数

　例としてアンケートで政党Aの支持率を調査して、標本1の標本比率とサンプル数=(0.33, 100)、標本２は(0.25, 100)としたときに有意差があるか確認しました。
　結果としてz値1.25<1.645でありp値>αのため帰無仮説は棄却できません。よって現状では標本に差があるとは判断できません（※くどいですが差が無いわけでなく統計的に判断できないだけです）。

[IN]
ratio_1=0.33 #標本1の比率
ratio_2=0.25 #標本2の比率
nums_sample1 = 100 #標本1のサンプル数
nums_sample2 = 100 #標本2のサンプル数

ratio_p = (ratio_1*nums_sample1 + ratio_2*nums_sample2) / (nums_sample1 + nums_sample2) #標本間の比率の平均
z= (ratio_1 - ratio_2) / np.sqrt(ratio_p*(1-ratio_p)*(1/nums_sample1 + 1/nums_sample2)) #z値
lim_z95_1side = stats.norm.ppf(0.95) #標準正規分布の95%点（上側）(PPF: Percent Point Function)
p_value = stats.norm.sf(np.abs(z)) #標準正規分布の累積分布関数（Cumulative Distribution Function）の逆関数

print(f'推定母比率p:{ratio_p:.3f}, z値:{z:.3f}')
print(f'片側95%点:{lim_z95_1side:.3f}, p値:{p_value:.3f}')

[OUT]
推定母比率p:0.290, z値:1.247
片側95%点:1.645, p値:0.106

　もしサンプル数を2倍に増やしても標本比率が変わらなければ有意差が出るようになります。よって、必要であればサンプル数を増やす必要があることが分かります。

[IN]
ratio_1=0.33 #標本1の比率
ratio_2=0.25 #標本2の比率
nums_sample1 = 200 #標本1のサンプル数
nums_sample2 = 200 #標本2のサンプル数

ratio_p = (ratio_1*nums_sample1 + ratio_2*nums_sample2) / (nums_sample1 + nums_sample2) #標本間の比率の平均
z= (ratio_1 - ratio_2) / np.sqrt(ratio_p*(1-ratio_p)*(1/nums_sample1 + 1/nums_sample2)) #z値
lim_z95_1side = stats.norm.ppf(0.95) #標準正規分布の95%点（上側）(PPF: Percent Point Function)
p_value = stats.norm.sf(np.abs(z)) #標準正規分布の累積分布関数（Cumulative Distribution Function）の逆関数

print(f'推定母比率p:{ratio_p:.3f}, z値:{z:.3f}')
print(f'片側95%点:{lim_z95_1side:.3f}, p値:{p_value:.3f}')

[OUT]
推定母比率p:0.290, z値:1.763
片側95%点:1.645, p値:0.039

　６－２－２．カイ二乗検定

　２グループ間の比率の差の検定は$${χ^2}$$検定でも可能である。$${χ^2}$$検定はZ検定とは別の観点から作られているが、２グループ間の比較であれば計算式は同じとなる。

$$ \chi^2 = \sum_{i=1}^{n} \frac{(O_i - E_i)^2}{E_i} $$

$${O_i}$$：観測値（カテゴリーで観測された度数）
$${E_i}$$：理論値/期待値（カテゴリーで期待される度数）
$${n}$$：カテゴリーの総数

　サンプルとして２グループ間に差があるかを確認した。結果としてp値=0.03%であり帰無仮説は棄却されるため有意差がありと判断できる。

[IN]
class HorizontalDisplay:
    def __init__(self, *args):
        self.args = args

    def _repr_html_(self):
        template = '<div style="float: left; padding: 10px;">{0}</div>'
        return "\n".join(template.format(arg._repr_html_())
                         for arg in self.args)

data = np.array([[44, 20],
                 [56, 80]])

df_origin = pd.DataFrame(data, columns=['プロパー', '転職組'], index=['優秀', '普通'])
df = df_origin.copy()
df['合計'] = df.sum(axis=1)
df_ideal = df.copy()
df_ideal['プロパー'], df_ideal['転職組'] = df_ideal['合計']/2, df_ideal['合計']/2

display(HorizontalDisplay(df_origin, df, df_ideal))

def calc_chi2dist(s1_T, s1_F, s2_T, s2_F):
    #カイ二乗分布の計算
    nums_T_total = s1_T + s2_T
    nums_F_total = s1_F + s2_F
    nums_T = nums_T_total/2
    nums_F = nums_F_total/2
    chi2 = (s1_T - nums_T)**2/nums_T + (s1_F - nums_F)**2/nums_F + (s2_T - nums_T)**2/nums_T + (s2_F - nums_F)**2/nums_F
    return chi2

s1_T, s2_T, s1_F, s2_F = data[0][0], data[0][1], data[1][0], data[1][1]
chi2 = calc_chi2dist(s1_T, s1_F, s2_T, s2_F)
p_value = stats.chi2.sf(chi2, 1) #カイ二乗分布の累積分布関数（Cumulative Distribution Function）の逆関数
print(f'カイ二乗値:{chi2:.3f}, p値:{p_value:.5f}')
    
[OUT]
カイ二乗値:13.235, p値:0.00027

６－３．母分散の差の検定：F検定

　母分散はF検定を使用します。F検定ではF分布を使用し、F分布は標本1,2それぞれの自由度の関数となります。

　ここでは簡易に結果だけ示します。下記条件では２標本間の母分に差はなく、ばらつきの違いはないと判断されました。

[IN]
data = np.array([[168.1, 9.78, 10],
                 [164.3, 11.54, 8]])

df = pd.DataFrame(data, columns=['標本平均', '不偏偏差', '標本数'], index=['標本1', '標本2'])
display(df)
d_free1, d_free2 = df['標本数'][0]-1, df['標本数'][1]-1
print(f'自由度1:{d_free1}, 自由度2:{d_free2}')

def calc_Fvalue(var1_unbiased, var2_unbiased):
    if var1_unbiased > var2_unbiased:
        F = var1_unbiased / var2_unbiased
    else:
        F = var2_unbiased / var1_unbiased
    return F

F = calc_Fvalue(df['不偏偏差'][0], df['不偏偏差'][1])
p_value = stats.f.sf(F, d_free2, d_free1) #F分布の累積分布関数（Cumulative Distribution Function）の逆関数
print(f'F値:{F:.3f}, p値:{p_value:.3f}')

[OUT]
	標本平均	不偏偏差	標本数
標本1	168.1	9.78	10.0
標本2	164.3	11.54	8.0

自由度1:9.0, 自由度2:7.0
F値:1.180, p値:0.399

６－４．補足：検定の多重性の問題

　６－１節では母平均の差を求めるために「等分散かどうかを判断」してZ検定かウェルチのt検定を使い分けました。論理的に考えれば「事前に母分散の検定」ー＞「検定結果に合わせて母平均の検定をどちらにするか判断」する流れになりますが、この場合検定を複数重ねることになり信頼性が低くなる問題があります。これを検定の多重性と言います。
　必ずしも母分散の検定が必要というわけでもないため、状況に応じて判断が必要になります。

７．多重比較法（Multiple Comparison Procedure）

　今までは２群間での差を検定しましたが、帰無仮説$${H_{0}:u_{1}=u_{2}}$$を棄却すると対立仮説$${H_{1}:u_{1}≠u_{2}}$$が採択されます。他群になると単純に帰無仮説$${H_{0}:u_{1}=u_{2}=u_{3}}$$を棄却しても対立仮説は複数あるためどこに有意差があるか特定できません。よって、他群の平均値の有意差検定にt検定は使用できません。
（※t検定は決められた２群間の有意差を確認するためのもの）
　多重比較の方法には次のようなものがあります。詳細はまだ理解できないため本章では紹介のみとなります。

ライヤン（Ryan）の方法
テューキー（Tukey）の方法
ダンカン（Cuncan）の方法
シェッフェ（Scheffe）の方法
最小有意差（LSD）法

参考資料

仮説検定など統計手法選択のフローチャートhttps://t.co/2ikn6t0i9j https://t.co/wcMq4ANfGI
「このページは大阪大学大学院薬学研究科・医薬情報解析学分野、大阪大学遺伝情報実験センター、大阪大学微生物病研究所で開発された、医薬学分野において必要な統計解析プログラムのサービスサイトです」 pic.twitter.com/DKqLqnjGNV
— 🎍QDくん🎍Python x 機械学習 x 金融工学 (@developer_quant) January 6, 2023

Python

データ用

https://dashboard.e-stat.go.jp/

あとがき

　追って追記予定

この記事が気に入ったらサポートをしてみませんか？