Pythonで学ぶ統計学２：母集団と標本／抽出

2023年1月3日 10:58

１．概要

　本記事は統計学の学習記録用として作成しており、私が理解するのに時間がかかった場所や追って参照したい内容を中心にまとめております。

　本記事のテーマは「母集団と標本／抽出」になります。
　参考として下記（CC-BY）を使用させていただきました。

１－１．記事説明：データとPythonライブラリ

　本記事で使用したサンプルデータを紹介します。本題ではないため詳細な説明は省きます。
　またPythonも使用していきますがライブラリの詳細説明は省きますので個別のライブラリは別記事で確認お願いします。なおScipyは(2023年1月現在)では記事を作成しておりませんがこちらも説明は省きます。

２．母集団と標本

２－１．母集団と標本の定義

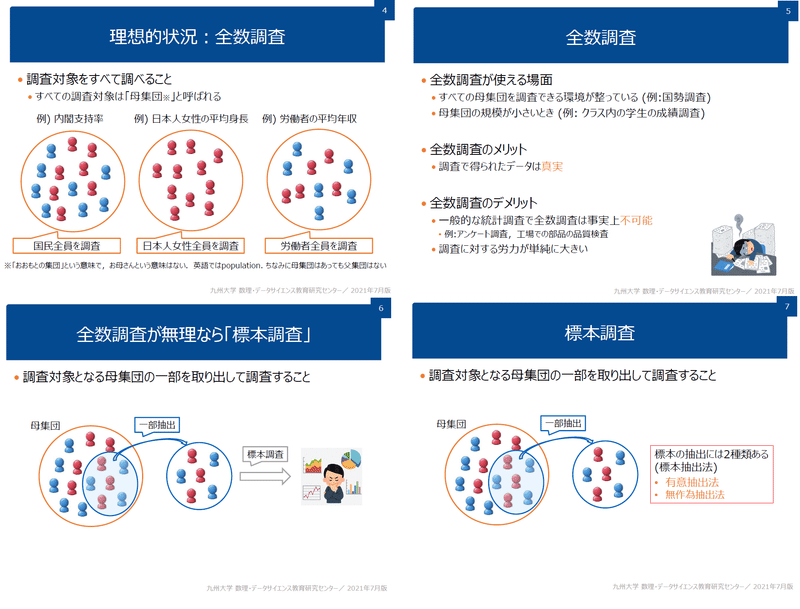
　データ群には母集団（Population)と標本(Sample)の２種類があります（出典：なるほど統計学園）。なお母集団の固有統計量（平均・分散など）を総称して母数(parameter)と呼びます。

母集団：対象となるデータ群の全体
標本：母集団の中からデータを一部抽出したデータ群

　母集団には「有限母集団」と「無限母集団」があり、それぞれの定義は下記の通りです。

●有限母集団：母集団のデータ数に限りがあるもの（例：日本の人口など）
●無限母集団：母集団のデータ数に限りがないもの（例：工場での運転データなど）

２－２．サンプルサイズ・サンプル数

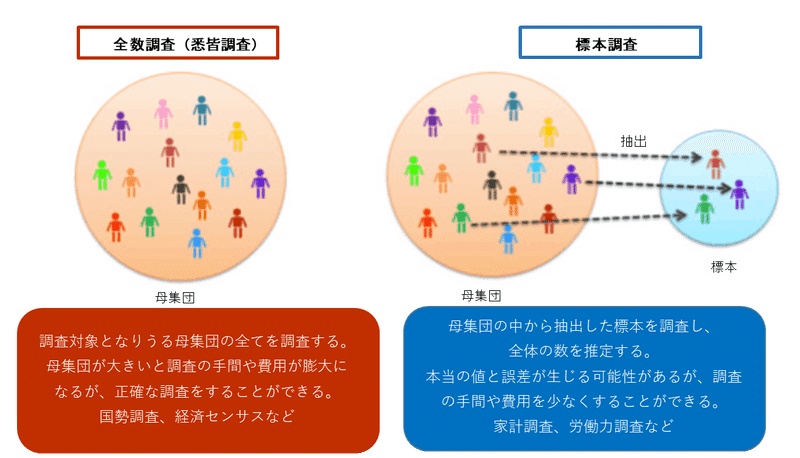
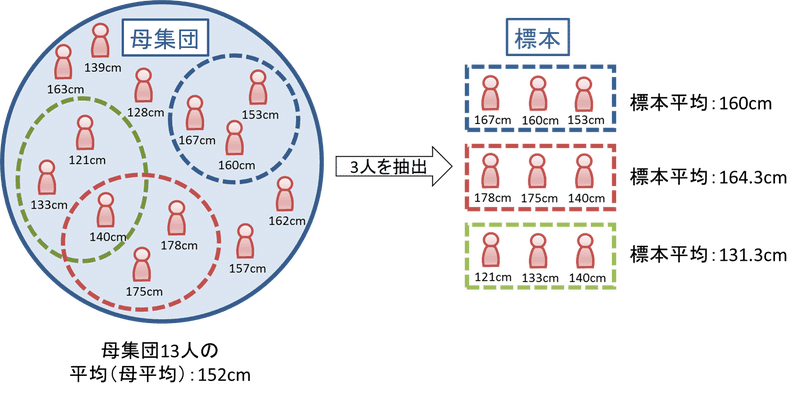
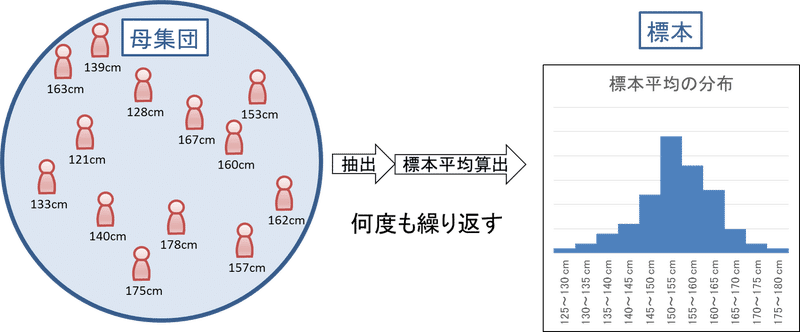
　母集団から抽出されたサンプルである標本には下記用語があります。下図の例だとサンプル数：1、サンプルサイズ：3となります。

サンプル数（標本数）：何回標本抽出を実施したか
サンプルサイズ：１回の標本抽出において抽出したデータ数

　なおサンプルサイズの決め方は難しく１つの学問としても成り立ちます。

２－３．標本平均と標本分散

　母集団＝集団の全数のため統計量（平均値$${\mu_p}$$、標準偏差$${\sigma_p}$$）は変化しません（全数取得すれば得られるデータに変化はないため）。
　しかし母集団から抽出される標本にばらつきが発生するため、標本の統計量は抽出ごとに変化します。従って「標本の平均値$${\mu_s}$$は(定数でなく)ばらつきを持った分布」でありこの分布を標本分布といいます。
　標本分布は下記の特徴があります。

母集団が正規分布である場合、標本平均も正規分布に従う
大数の法則より、標本数$${n}$$が大きくなれば標本平均$${\mu_s}$$は母平均$${\mu_p}$$に近づく
中心極限定理より、母集団に特定の分布がなくても標本数が大きくなれば標本平均は正規分布に従う
標本平均の標準偏差は標本数nに合わせて$${\frac{1}{\sqrt{n}}}$$だけ小さくなる（標本数が大きいとばらつきが小さくなる）
母集団が事前にわかっている状況はまれであり、通常は標本のデータしか取れない。この時標準平均が正規分布に従うとしても真の母集団の$${\mu_p}$$、$${\sigma_p}$$（つまり分布）はわからない。

【補足】
　上記に関して一部補足を記載します。くどい説明にはなりますが、私が勘違いしていた部分も含めて追記しました。

標本数$${n}$$が大きくなる時に正規分布に従うのは標本平均の分布です。母集団の分布が正規分布であるかが分かるわけではありません（そもそも推定・検定では母集団の分布は不明であり、分布は仮定して推定・検定を実施する）。
中心極限定理より、母集団の分布が正規分布でなくても標本平均の分布が正規分布に従う（母集団の分布が正規分布に従うわけではない）。
中心極限定理における、標本平均の分布は「平均：μ、標準偏差：標準誤差$${\frac{\sigma}{\sqrt{n}}}$$」に従う。よって、サンプル数nが増えると分散が小さくなるため標本平均の分布のばらつきは小さくなる

$$
標準誤差（SE：standard error）：\sqrt{\frac{分散}{サンプル数}}=\sqrt{\frac{\sigma^2}{n}}=\frac{\sigma}{\sqrt{n}}
$$

（出典：17. 大数の法則と中心極限定理）

２－３．標本分布の確認

　数値計算で標本抽出を実施して下記を検証しました。

（A）標本平均の平均・分散はばらつく
（B）標本平均には分布が存在し、確率分布として存在する

【シミュレーションのフロー】

母集団の作成：正規分布のデータを作成するためnp.random.randn()で1億個のデータを作成（平均0, 標準偏差1になる程度に大きなサンプルを作成）。これを母集団と考える。
標本の作成：母集団から標本数=1000で無作為抽出（ランダム）
可視化：データの分布をヒストグラムで可視化（ヒストグラムのため縦軸は確率密度ではなく相対度数です。標本同士は階級(bins)が同じため比較できますが正規分布との比較はできません。）

　結果として各抽出ごとで分布も平均値・分散も異なることが分かります。つまり標本から得られる値は定数ではなく（母集団をベースとした）分布として考える必要があるということが分かります。
　通常は母集団は不明であり標本しかわからないことが多いため、標本から母集団の統計量を推定することが重要になります（母集団の分布は不明のため、あくまで母数（平均値や分散）を推定します）。

[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import os 
from scipy import stats
from typing import List

np.random.seed(123)

def showGraph(xs: List, ys: List, labels: List, verbose=False):
    fig = plt.figure(figsize=(10, 6), facecolor='w')
    ax = fig.add_subplot(111)
    
    colors = {0:'red', 1:'blue', 2:'green', 3:'orange'}
    idx = 0
    #確率密度分布 
    for x, y, label in zip(xs, ys, labels):
        #分布を表示 
        ax.plot(x, y, label=label, color=colors[idx])
        
        idx += 1

    #x軸の作成 
    tick_x = np.array(xs).max()
    tick_xs = np.arange(-int(tick_x), int(tick_x)+0.5, 0.5)

    #体裁調整 
    ax.set(xlabel='x(データ)', ylabel='頻度', 
           xticks=tick_xs,
           xlim=(tick_xs.min(), tick_xs.max()))
    plt.title(f'正規分布の母集団と標本の確率分布', y=-0.15)
    plt.grid()
    plt.legend()
    if verbose:
        if os.path.exists('image') == False:
            os.mkdir('image') #imageフォルダがなければ作成 
        plt.savefig(f'image/確率密度_{label}.png')
        
    plt.show()
    
 #母集団 
nums = int(1e8)
y = np.random.randn(nums) #標準正規分布に従う乱数を大量に生成 (母集団)
freqs, _x = np.histogram(y, bins=20) #ヒストグラムを作成 
probs = freqs / nums #確率密度を計算 
x = (_x[1:] + _x[:-1]) / 2 #x軸の値を計算 
 #標本 
nums_s = 1000 #標本数 
sample_1 = np.random.choice(y, size=nums_s, replace=False) #標本抽出 
sample_2 = np.random.choice(y, size=nums_s, replace=False) #標本抽出 
sample_3 = np.random.choice(y, size=nums_s, replace=False) #標本抽出 

freqs1, _x1 = np.histogram(sample_1, bins=20) #ヒストグラムを作成 
freqs2, _x2 = np.histogram(sample_2, bins=20) #ヒストグラムを作成 
freqs3, _x3 = np.histogram(sample_3, bins=20) #ヒストグラムを作成 ]\
probs1, probs2, probs3 = freqs1 / nums_s, freqs2 / nums_s, freqs3 / nums_s #確率密度を計算 
x1_s, x2_s, x3_s = (_x1[1:] + _x1[:-1]) / 2, (_x2[1:] + _x2[:-1]) / 2, (_x3[1:] + _x3[:-1]) / 2 #x軸の値を計算 


xs = [x, x1_s, x2_s, x3_s]
ys = [probs, probs1, probs2, probs3]
labels = ['母集団', '標本1', '標本2', '標本3']

print(f'母集団平均値:{y.mean():.2f}, 母集団標準偏差:{y.std():.2f}')
print(f'標本1平均値:{sample_1.mean():.2f}, 標本1標準偏差:{sample_1.std():.2f}')
print(f'標本2平均値:{sample_2.mean():.2f}, 標本2標準偏差:{sample_2.std():.2f}')
print(f'標本3平均値:{sample_3.mean():.2f}, 標本3標準偏差:{sample_3.std():.2f}')

showGraph(xs, ys, labels, verbose=True)


[OUT]
母集団平均値:0.00, 母集団標準偏差:1.00
標本1平均値:-0.01, 標本1標準偏差:1.01
標本2平均値:-0.00, 標本2標準偏差:0.99
標本3平均値:0.01, 標本3標準偏差:1.03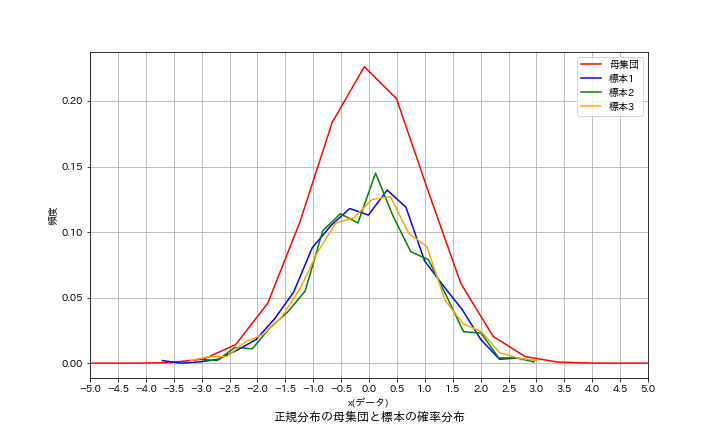

３．標本抽出

　前章で母集団と標本の違いと標本抽出を説明しました。標本抽出において重要な法則を紹介します。

３－１．大数の法則

　大数の法則とは「ある独立した試行においてその事象が発生する確率p（または期待値E）とすると、試行回数nが大きくなるにつれて事象の発生確率がp(またはE)に近づいていくこと。」です。つまり「標本数nが大きくなれば標本平均$${\mu_s}$$は母平均$${\mu_p}$$に近づく」ことを意味します。
　なおこれは母平均を定数（特定の値）とみなすため「記述統計」や「推測統計の点推定」に該当し、推定・検定での概念とは異なることに注意が必要です。

【大数の法則をシミュレーション】
　条件として6面さいころの期待値を求めます。理論値は下記の通り3.5となります。　標本数が大きくなれば標本平均のばらつき$${\sigma_s}$$が小さくなり、平均値は母平均$${\mu_p}$$に近づいていることが確認できます。

$$
E(X) = \frac{1}{6} \cdot 1 + \frac{1}{6} \cdot 2 + \frac{1}{6} \cdot 3 + \frac{1}{6} \cdot 4 + \frac{1}{6} \cdot 5 + \frac{1}{6} \cdot 6=3.5
$$

[IN]
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

np.random.seed(135)

class ThrowDice:
    def __init__(self, ):
        self.diceNo = np.arange(1, 7) # 1~6のサイコロの目
        self.deceprob = np.full(6, 1/6) # 6面の確率を同じにする
        
    def __call__(self, nums):
        output = np.random.choice(self.diceNo, nums, p=self.deceprob)  
        return output
    
dice = ThrowDice()
result = dice(5)
print(f'試行回数5の結果: {result}, 期待値: {result.mean()}')

nums_throws = 300
dice_throws = np.array([dice(num).mean() for num in range(1, nums_throws+1)]) # 1~99回投げた結果を配列にする
 #可視化 
fig = plt.figure(figsize=(12, 6), facecolor='w')
ax = fig.add_subplot(111)
ax.plot(dice_throws, label='平均値', linewidth=1)
ax.plot(np.full(nums_throws, 3.5), 'r--', label='理論値', linewidth=1)
ax.set(xlabel='試行回数n(サイコロをなげた回数)', ylabel='平均値μ', title='さいころをn回投げた結果の平均値μの推移',
       xticks=np.arange(0, nums_throws+1, 10), yticks=np.arange(0, 6.5, 0.5))
plt.legend(), plt.grid()
plt.show()


[OUT]
試行回数5の結果: [4 2 2 6 5], 期待値: 3.8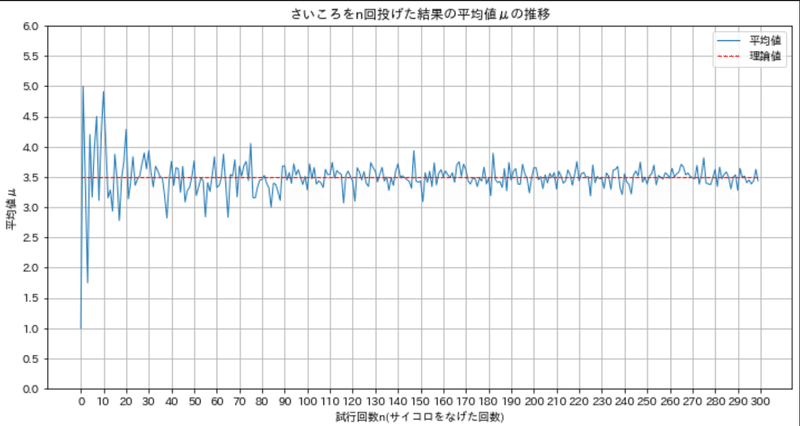

３－２．中心極限定理

　中心極限定理とは「母集団が未知でも、標本数nが大きくなれば標本平均の分布は下記の正規分布に従う」です。ポイントは下記の通りです。

「nが増えると平均は母平均$${\mu}$$に近づき、分散はnが増える分だけ母分散$${\sigma^2}$$から$${\frac{1}{n}}$$だけ小さくなる」ことと同義です
本定義ではサンプルサイズ(標本数)nに依存する式であり、サンプル数（標本数）は影響しません。ただしシミュレーションをする場合は、標本分布を取得するため標本数はたくさん必要です（後述参照）。

$$
中心極限定理における標本分布\mathcal{N(\mu, \frac{\sigma^2}{n})}=\dfrac{1}{\sqrt{2\pi\frac{\sigma}{\sqrt{n}}}}\exp(-\dfrac{(x-\mu)^ 2}{2\frac{\sigma^2}{n}})
$$

$$
標本平均の分布の分散=\frac{\sigma^2}{n}
$$

$$
標本平均の分布の標準偏差=\frac{\sigma}{\sqrt{n}}
$$

母平均：$${\mu}$$、母分散：$${\sigma^2}$$、サンプルサイズ：$${n}$$、正規分布：$${\mathcal{N(平均, 分散)}}$$

$$
通常の正規分布\mathcal{N(\mu, \sigma^2)}=\dfrac{1}{\sqrt{2\pi\sigma^ 2}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})
$$

　中心極限定理を理解するためにシミュレーションを実施します。

　３－２－１．数値計算１：サンプル作成

　下記条件で母集団と標本抽出を実施しました。結果として(標本数, 標本サイズ)の形状をもつ配列を作成できました。コードの動作や注意点も合わせて下記に記載します。
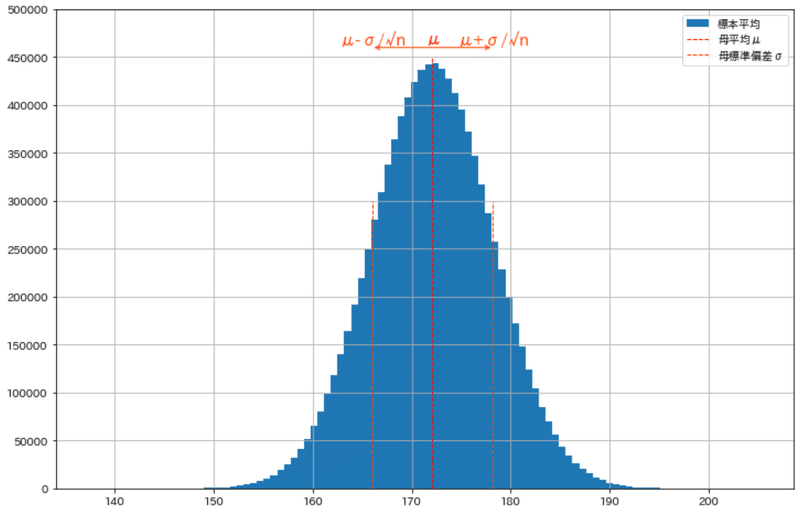
　参考までにコードは記載しておりませんが母集団は下図の通りです。

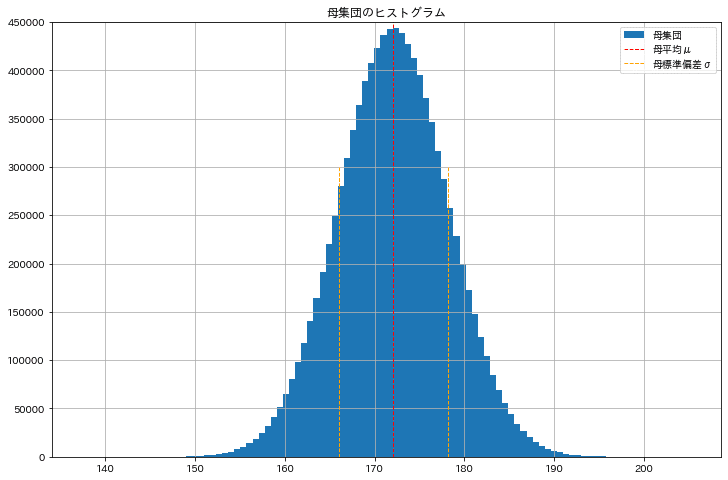
【シミュレーションの条件：30-39歳の男性の身長】
●母集団の平均値、標準偏差、サンプル数：μ=172.1、σ=6.1, 全数=1000万
●標本サイズ＝4～100万（計：7パターン）
●標本数=5, 100（中心極限定理での標本分布の正規分布に影響しませんが、標本分布を作るために数がいることを確認するために２種作成）

【Pythonコードの動作内容】
１．指定した平均値、標準偏差、サンプル数の母集団を正規分布で作成
２．標本抽出より、標本サイズ7種×標本数2種＝計14パターンを作成
３．出力値の確認（標本の形状、最小標本(標本数：4, 標本サイズ：5))

【注意点】
●標本数が大きいほどきれいな標準平均の分布を作成（分布に使用する標本平均の数が増えるため）できますが、標本抽出(samplingメソッド)をfor文で作成しており時間がかかります。高速化しきれなかったため、今回は標本数=100で計算しました。
●この時点では母集団から標本を抽出しただけのため、標本があるだけであり標本平均（の分布）ではありません。

[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import re
import time

np.random.seed(135)

class GetSample:
    def __init__(self, mean_p, std_p, size_population):
        self.mean_p = mean_p #母平均 
        self.std_p = std_p #母分散の標準偏差 
        self.size_population = size_population #標本サイズ 
        
        self.population = np.random.normal(self.mean_p, self.std_p, size_population) #母集団を作成 
    
    def sampling(self, sample_size, nums_sample):
        output = [np.random.choice(self.population, sample_size, replace=False) for _ in range(nums_sample)] #replace =Falseで重複なし
        return np.array(output)
    
 #母集団の作成 
mean, std, size_population = 172.1, 6.1, int(1e7)
data_p = GetSample(mean, std, size_population)
population = data_p.population
print(f'母数 n:{len(population)}, μ：{population.mean():.2f}, var:{population.var():.2f}, σ：{population.std():.2f}') 
 #サンプル数を設定 
num_samples_little, num_samples = 5, 100
 #標本数 （サンプルサイズ）を設定
s_size4, s_size25, s_size100, s_size400, s_size1e4, s_size1e5, s_size1e6 = 4, 25, 100, 400, int(1e4), int(1e5), int(1e6) #標本抽出 (標本数:5)
_starttime = time.time()
data_s4_little, data_s25_little, data_s100_little, data_s400_little, data_s1e4_little, data_s1e5_little, data_s1e6_little = data_p.sampling(s_size4, num_samples_little), data_p.sampling(s_size25, num_samples_little), data_p.sampling(s_size100, num_samples_little), data_p.sampling(s_size400, num_samples_little), data_p.sampling(s_size1e4, num_samples_little), data_p.sampling(s_size1e5, num_samples_little), data_p.sampling(s_size1e6, num_samples_little)
print(f'処理時間(標本数={num_samples_little})：{time.time() - _starttime:.2f}sec') #標本抽出 (標本数:100)
_starttime = time.time()
data_s4, data_s25, data_s100, data_s400, data_s1e4, data_s1e5, data_s1e6 = data_p.sampling(s_size4, num_samples), data_p.sampling(s_size25, num_samples), data_p.sampling(s_size100, num_samples), data_p.sampling(s_size400, num_samples), data_p.sampling(s_size1e4, num_samples), data_p.sampling(s_size1e5, num_samples), data_p.sampling(s_size1e6, num_samples)
print(f'処理時間(標本数={num_samples})：{time.time() - _starttime:.2f}sec')
 #データの形状確認 
print(f'データ形状(標本数={num_samples_little})：{data_s4_little.shape}, {data_s25_little.shape}, {data_s100_little.shape}, {data_s400_little.shape}, {data_s1e4_little.shape}, {data_s1e5_little.shape}, {data_s1e6_little.shape}')
print(f'データ形状(標本数={num_samples})：{data_s4.shape}, {data_s25.shape}, {data_s100.shape}, {data_s400.shape}, {data_s1e4.shape}, {data_s1e5.shape}, {data_s1e6.shape}')
 #参考用としてDataFrame作成 
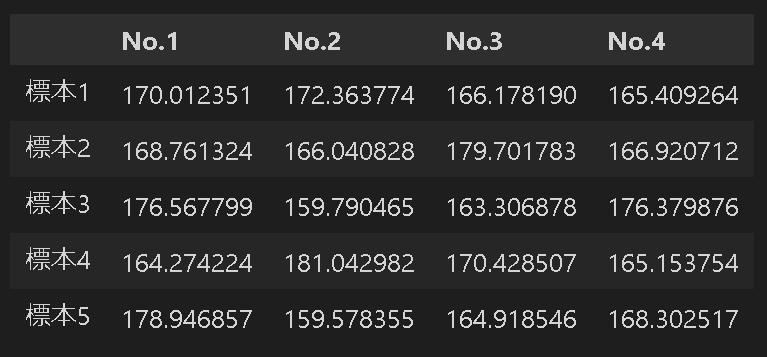
df_s4little = pd.DataFrame(data_s4_little, 
                  columns=[f'No.{i}' for i in range(1, s_size4+1)],
                  index=[f'標本{i+1}' for i in range(num_samples_little)])

display(df_s4little)

[OUT]
母数 n:10000000, μ：172.10, var:37.18, σ：6.10
処理時間(標本数=5)：12.99sec
処理時間(標本数=100)：264.34sec
データ形状(標本数=5)：(5, 4), (5, 25), (5, 100), (5, 400), (5, 10000), (5, 100000), (5, 1000000)
データ形状(標本数=100)：(100, 4), (100, 25), (100, 100), (100, 400), (100, 10000), (100, 100000), (100, 1000000)

標本サイズ：4、標本数：５の出力

　３－２－２．標本平均の分布を作成

　抽出した標本から標本平均の分布を作成します。具体的には前述で取得した配列は行方向に標本が並ぶため、Numpyのaxis=1で列方向に平均と分散を計算します。

　本コードでは概要として下記を実施しました。なおイメージとして標本数5、標本サイズn=4のパターンを図示しました。

各標本(計14パターン)において、配列の表方向の平均を計算して標本平均の分布を計算（mean(axix=1)後に行方向に標準平均の配列が生成）
標本平均の分布の（平均値、分散）を計算
中心極限定理における”標本平均の分布”の平均値=母平均、分散=$${\frac{\sigma^2}{n}}$$を計算
テーブルデータとして確認できるようにDataFrame化

　結果として下記が確認できました。

標本サイズが大きくても標本数が小さいと、標本分布にならない。
標本数を大きくすると「標本平均の分布の平均値（各標本内で計算した平均値の平均）」は母平均μに近くなる。
標本数を大きくしたとき、「標本平均の分布の分散」は$${\frac{\sigma^2}{n}}$$に近くなる。
（後述しますが）「標本平均の分布」は正規分布に従う。

[IN]
pd.options.display.float_format = '{:.2f}'.format
 #標本分布の作成 ：標本の平均値を計算
meandist_s4_little, meandist_s25_little, meandist_s100_little, meandist_s400_little, meandist_s1e4_little, meandist_s1e5_little, meandist_s1e6_little = data_s4_little.mean(axis=1), data_s25_little.mean(axis=1), data_s100_little.mean(axis=1), data_s400_little.mean(axis=1), data_s1e4_little.mean(axis=1), data_s1e5_little.mean(axis=1), data_s1e6_little.mean(axis=1)
meandist_s4, meandist_s25, meandist_s100, meandist_s400, meandist_s1e4, meandist_s1e5, meandist_s1e6 = data_s4.mean(axis=1), data_s25.mean(axis=1), data_s100.mean(axis=1), data_s400.mean(axis=1), data_s1e4.mean(axis=1), data_s1e5.mean(axis=1), data_s1e6.mean(axis=1)
 #まとめ参考用 ：DataFrame作成
_data = np.array([meandist_s4_little, meandist_s25_little, meandist_s100_little, meandist_s400_little, meandist_s1e4_little, meandist_s1e5_little, meandist_s1e6_little])
_s = np.array([s_size4, s_size25, s_size100, s_size400, s_size1e4, s_size1e5, s_size1e6])
_data = np.concatenate([_s.reshape(-1, 1), _data], axis=1)
_cols = ['サンプルサイズn'] + [f'標本平均{i}' for i in range(1, num_samples_little+1)]
df = pd.DataFrame(_data, columns=_cols)
display(df)
 #標本分布の平均・分散・標準偏差を計算 
mean_s4_little, mean_s25_little, mean_s100_little, mean_s400_little, mean_s1e4_little, mean_s1e5_little, mean_s1e6_little = meandist_s4_little.mean(), meandist_s25_little.mean(), meandist_s100_little.mean(), meandist_s400_little.mean(), meandist_s1e4_little.mean(), meandist_s1e5_little.mean(), meandist_s1e6_little.mean()
var_s4_little, var_s25_little, var_s100_little, var_s400_little, var_s1e4_little, var_s1e5_little, var_s1e6_little = meandist_s4_little.var(), meandist_s25_little.var(), meandist_s100_little.var(), meandist_s400_little.var(), meandist_s1e4_little.var(), meandist_s1e5_little.var(), meandist_s1e6_little.var()
std_s4_little, std_s25_little, std_s100_little, std_s400_little, std_s1e4_little, std_s1e5_little, std_s1e6_little = meandist_s4_little.std(), meandist_s25_little.std(), meandist_s100_little.std(), meandist_s400_little.std(), meandist_s1e4_little.std(), meandist_s1e5_little.std(), meandist_s1e6_little.std()

mean_s4, mean_s25, mean_s100, mean_s400, mean_s1e4, mean_s1e5, mean_s1e6 = meandist_s4.mean(), meandist_s25.mean(), meandist_s100.mean(), meandist_s400.mean(), meandist_s1e4.mean(), meandist_s1e5.mean(), meandist_s1e6.mean()
var_s4, var_s25, var_s100, var_s400, var_s1e4, var_s1e5, var_s1e6 = meandist_s4.var(), meandist_s25.var(), meandist_s100.var(), meandist_s400.var(), meandist_s1e4.var(), meandist_s1e5.var(), meandist_s1e6.var()
std_s4, std_s25, std_s100, std_s400, std_s1e4, std_s1e5, std_s1e6 = meandist_s4.std(), meandist_s25.std(), meandist_s100.std(), meandist_s400.std(), meandist_s1e4.std(), meandist_s1e5.std(), meandist_s1e6.std()
 #DataFrame作成 
columns = ['標本数', 'サンプルサイズ', '標本平均', '分散', '標準偏差']
_n = np.concatenate([np.full(7, num_samples_little), np.full(7, num_samples)], axis=0)
_size = np.array([s_size4, s_size25, s_size100, s_size400, s_size1e4, s_size1e5, s_size1e6]*2) #axis =1で各行(標本ごと)の平均、分散、標準偏差を計算しているため、標本分布の平均、分散、標準偏差を計算する
_mean = [mean_s4_little, mean_s25_little, mean_s100_little, mean_s400_little, mean_s1e4_little, mean_s1e5_little, mean_s1e6_little, mean_s4, mean_s25, mean_s100, mean_s400, mean_s1e4, mean_s1e5, mean_s1e6]
_var = [var_s4_little, var_s25_little, var_s100_little, var_s400_little, var_s1e4_little, var_s1e5_little, var_s1e6_little, var_s4, var_s25, var_s100, var_s400, var_s1e4, var_s1e5, var_s1e6]
_std = [std_s4_little, std_s25_little, std_s100_little, std_s400_little, std_s1e4_little, std_s1e5_little, std_s1e6_little, std_s4, std_s25, std_s100, std_s400, std_s1e4, std_s1e5, std_s1e6]
_data = np.array([_n, _size, _mean, _var, _std]).T
df = pd.DataFrame(_data, columns=columns) #中心極限定理による理論値を追加 
df['母平均'] = mean
df['理論分散'] = std**2/df['サンプルサイズ']
df['理論σ'] = df['理論分散'].apply(np.sqrt)
 #カラムの調整 
cols = [['標本抽出の条件', '標本抽出の条件', '標本分布', '標本分布', '標本分布', '中心極限定理', '中心極限定理', '中心極限定理'],
        ['標本数', 'サンプルサイズ', '標本平均', '分散', '標準偏差', '母平均', '理論分散', '理論σ']]
df.columns = cols
df

[OUT]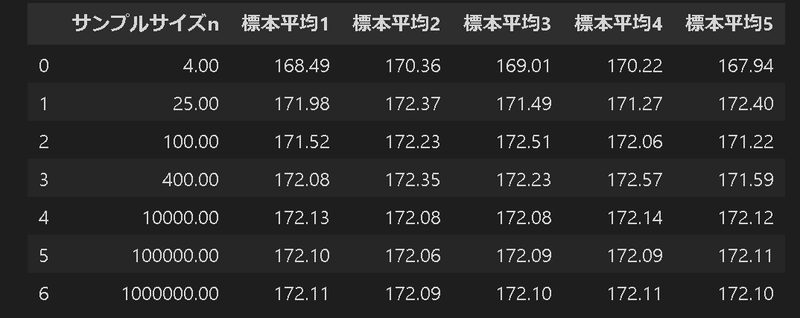

　３－２－３．可視化1：標本平均の分布のヒストグラム

　標本平均の分布を取得できましたのでヒストグラムで可視化しました。結果として下記が確認できました。

標本数が小さいと標本平均の分布は不明（ヒストグラム化できるほどのデータ数にならないため）
標本数が十分な場合において、サンプル数nが増えると”標本平均の分布”は釣り鐘型となり正規分布に従う。
標本数が十分な場合において、サンプル数nが増えると”標本平均の分布”の分散は小さくなる。つまりサンプル数nが大きいなら、（分布の幅が小さくなるため）標本平均は母平均に近くなる。

[IN]
def generate_tick(num):
    if num<10:
        return 1
    elif 10<num<30:
        return 2
    elif 30<num<100:
        return 5
    elif 100<num<300:
        return 10
    
data_plot = [meandist_s4_little, meandist_s25_little, meandist_s100_little, meandist_s400_little, meandist_s1e4_little, meandist_s1e5_little, meandist_s1e6_little]
label = ['size=5, n=4', 'size=5, n=25', 'size=5, n=100', 'size=5, n=400', 'size=5, n=1000', 'size=5, n=1e4', 'size=5, n=1e5']

fig, axs = plt.subplots(2, 4, figsize=(20, 12), facecolor='w', edgecolor='k')
for idx, (data, label) in enumerate(zip(data_plot, label)):
    ax = axs[idx//4, idx%4]
    Y, X, _ = ax.hist(data, bins=20, density=False, 
                      range=(167, 177), label=label, ec='navy')
    
    #体裁調整 
    y_max, y_min = int(max(Y)) + 1, int(min(Y))
    tick = generate_tick(y_max)
    ax.set_yticks(np.arange(0, y_max+1, tick))
    ax.set_xticks(np.arange(167, 178, 1))
    ax.vlines(mean, 0, y_max, color='red', label='母平均', ls='dashed')
    ax.set_xlabel('標本平均')
    ax.set_ylabel('度数')
    ax.legend(loc='upper right')
    
    if idx==6:
        ax = axs[1, 3]
        Y, X, _ = ax.hist(data_plot, bins=10, density=False, label='全データ')
        ax.set_xlabel('標本平均')
        ax.set_ylabel('度数')
        ax.legend(loc='upper right')

plt.tight_layout()
plt.suptitle(f'標本平均のヒストグラム（標本数：{num_samples_little}, 標本サイズ:{s_size4}～{format(s_size1e6, ",")}）', fontsize=20, y=-0.01)

 #標本数 ：１００
data_plot = [meandist_s4, meandist_s25, meandist_s100, meandist_s400, meandist_s1e4, meandist_s1e5, meandist_s1e6]
label = ['size=100, n=4', 'size=100, n=25', 'size=100, n=100', 'size=100, n=400', 'size=100, n=1000', 'size=100, n=1e4', 'size=100, n=1e5']

fig, axs = plt.subplots(2, 4, figsize=(20, 12), facecolor='w', edgecolor='k')
for idx, (data, label) in enumerate(zip(data_plot, label)):
    ax = axs[idx//4, idx%4]
    Y, X, _ = ax.hist(data, bins=20, density=False, 
                      range=(167, 177), label=label, ec='navy')
    
    #体裁調整 
    y_max, y_min = int(max(Y)) + 1, int(min(Y))
    tick = generate_tick(y_max)
    ax.set_yticks(np.arange(0, y_max+1, tick)) # １刻みにしても見にくいので２刻みにします
    ax.set_xticks(np.arange(167, 178, 1))
    ax.vlines(mean, 0, y_max, color='red', label='母平均', ls='dashed')
    ax.set_xlabel('標本平均')
    ax.set_ylabel('度数')
    ax.legend(loc='upper right')
    
    if idx==6:
        ax = axs[1, 3]
        Y, X, _ = ax.hist(data_plot, bins=10, density=False, label='全データ')
        ax.set_xlabel('標本平均')
        ax.set_ylabel('度数')
        ax.legend(loc='upper right')

plt.tight_layout()
plt.suptitle(f'標本平均のヒストグラム（標本数：{num_samples}, 標本サイズ:{s_size4}～{format(s_size1e6, ",")}）', fontsize=20, y=-0.01)


[OUT]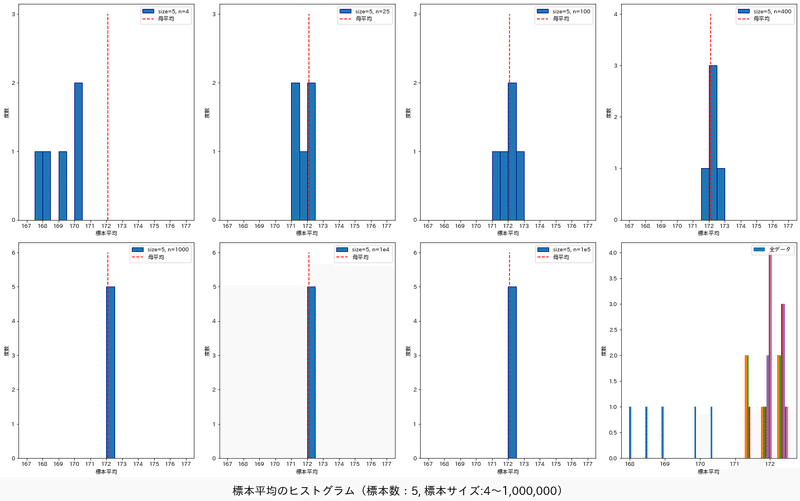

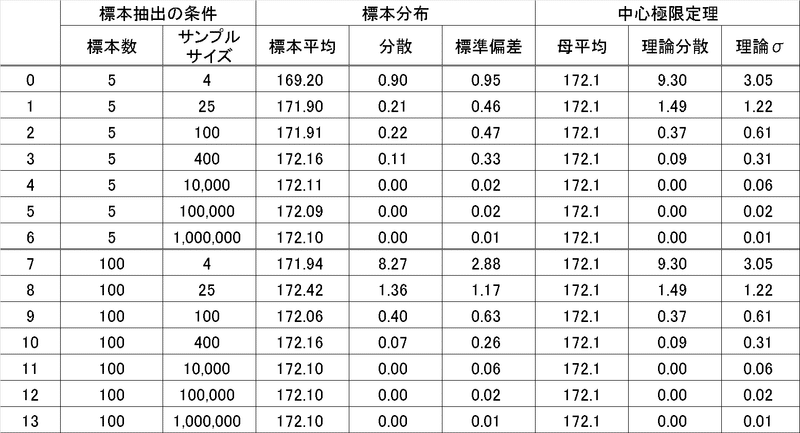
　３－２－４．可視化２：標本平均の分布の確率密度関数

　ヒストグラムと同様ですが、標本数が大きい(100)の時において確率密度関数がどのようになるかを確認しました。
　結論は同じであり①標本分布は正規分布に従う、②標本数nが増えると標本平均の分布は母平均に近づく、③標本数nが大きいほど標本分布の幅が小さくなり分散は$${\frac{\sigma^2}{n}}$$となります。

[IN] #標本数 ：１００
probdense_s4, bins_s4 = np.histogram(meandist_s4, bins=20, density=True)
probdense_s25, bins_s25 = np.histogram(meandist_s25, bins=20, density=True)
probdense_s100, bins_s100 = np.histogram(meandist_s100, bins=20, density=True)
probdense_s400, bins_s400 = np.histogram(meandist_s400, bins=20, density=True)
probdense_s1e4, bins_s1e4 = np.histogram(meandist_s1e4, bins=20, density=True)
probdense_s1e5, bins_s1e5 = np.histogram(meandist_s1e5, bins=20, density=True)
probdense_s1e6, bins_s1e6 = np.histogram(meandist_s1e6, bins=20, density=True)
 
data_plot = [probdense_s4, probdense_s25, probdense_s100, probdense_s400, probdense_s1e4, probdense_s1e5, probdense_s1e6]
bins_plot = [bins_s4, bins_s25, bins_s100, bins_s400, bins_s1e4, bins_s1e5, bins_s1e6]
label = ['size=100, n=4', 'size=100, n=25', 'size=100, n=100', 'size=100, n=400', 'size=100, n=1000', 'size=100, n=1e4', 'size=100, n=1e5']

fig, axs = plt.subplots(2, 4, figsize=(23, 14), facecolor='w', edgecolor='k')
for idx, (data, bins, label) in enumerate(zip(data_plot, bins_plot, label)):
    ax = axs[idx//4, idx%4]
    ax.plot(bins[:-1], data, label=label)
    
    #母集団情報を描写 
    sample_size = int(float(re.findall(r'n=(\d+e?\d*)', label)[0])) #正規表現でlabelからnの値を取得 
    calc_std = std/np.sqrt(sample_size)
    y_max = max(data)
    ax.vlines(mean, 0, y_max, color='red', label='母平均', ls='dashed')
    ax.vlines(mean+calc_std, 0, y_max, color='green', label='母標準偏差', ls='dashed')
    ax.vlines(mean-calc_std, 0, y_max, color='green', ls='dashed')
    ax.text(mean, y_max*1.05, f'μ：{mean:.2f}', fontsize=12, color='red')
    ax.text(mean+calc_std, y_max*0.8, f'σ：{calc_std:.2f}', fontsize=12, color='green')
    
    #図の体裁調整 
    ax.set_xlabel('標本平均')
    ax.set_ylabel('確率密度')
    ax.set_xticks(np.arange(165, 180, 1))
    ax.legend(loc='upper right'), ax.grid()

plt.tight_layout()
plt.suptitle(f'標本平均の確率密度分布（標本数：{num_samples}, 標本サイズ:{s_size4}～{format(s_size1e6, ",")}）', fontsize=20, y=-0.01)

[OUT]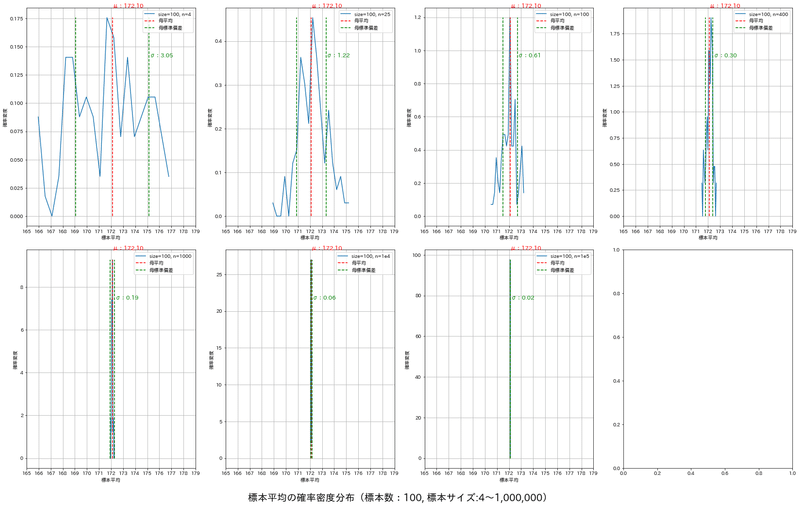

４．標本抽出（サンプリング）

　統計調査では時間・コストの面で全数（母集団）調査は難しいため、一般的には一部だけ抽出、つまり標本抽出（調査）を行います。
　要素はランダムに抽出される必要があり、十分にランダムに抽出された標本を無作為標本（確率標本）と呼びます。
　統計解析するデータは①バイアスがない、②ランダムでサンプリング　する必要性がありこの２つが成立していないと統計解析そのものに意味(価値)がありません。つまり標本抽出（データ取得）は非常に重要な条件であり、統計云々の前に正常なデータを取得・チェックできる必要があります。

４－１．抽出法の概要

　標本調査を行うために母集団から標本を抽出する手法としては「有意抽出法」と「無作為抽出法」があります。

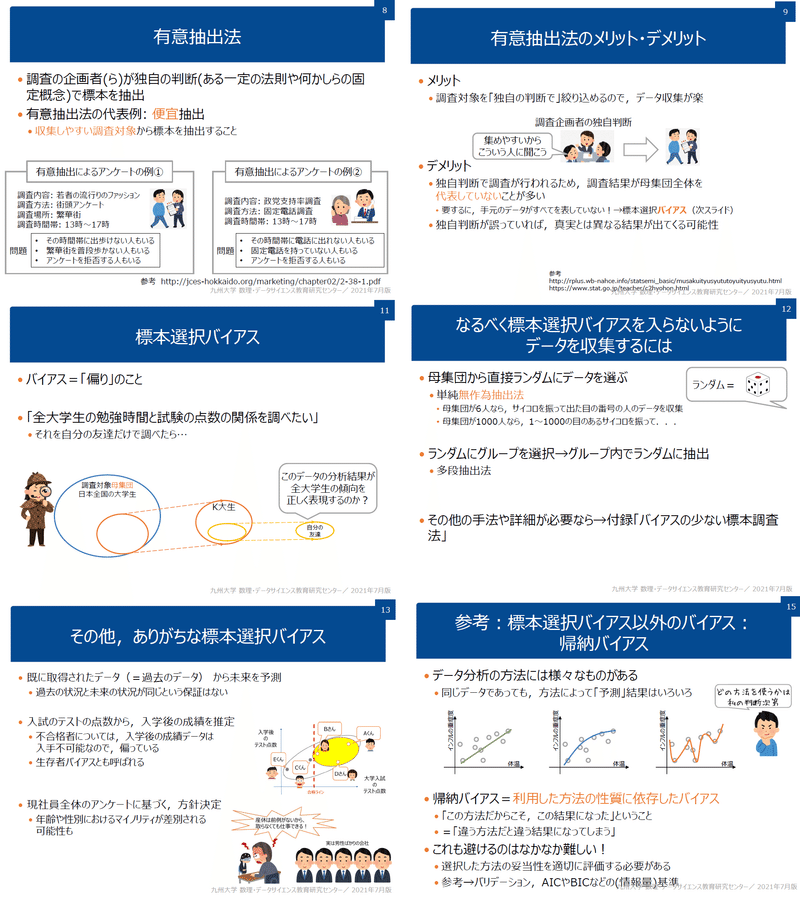
http://mdsc.kyushu-u.ac.jp/wp/wp-content/uploads/2021/08/f84d5a932fac29fbcda3cde3be78e52f.pdf

４－２．無作為抽出

　標本を抽出する時に重要なのは母集団と同じ偏りにすることです。無作為抽出とは、標本調査を行うときの標本の選び方の一つで、選ぶ際の恣意性をなくし全く確率的に母集団から選ぶ方法です。抽出法には下記があります。

（単純）無作為抽出
層化抽出法（層別抽出法）
クラスター抽出法（集落抽出法）
多段抽出法
系統抽出法
二相抽出法

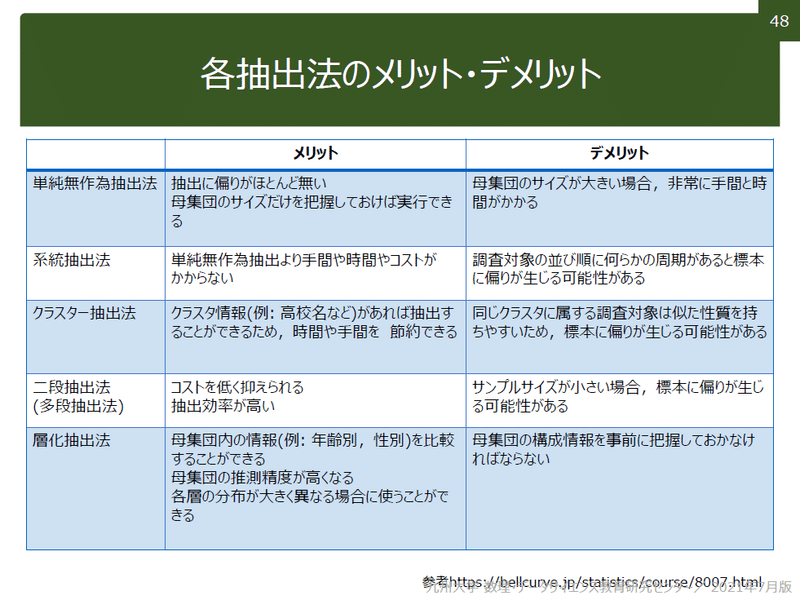
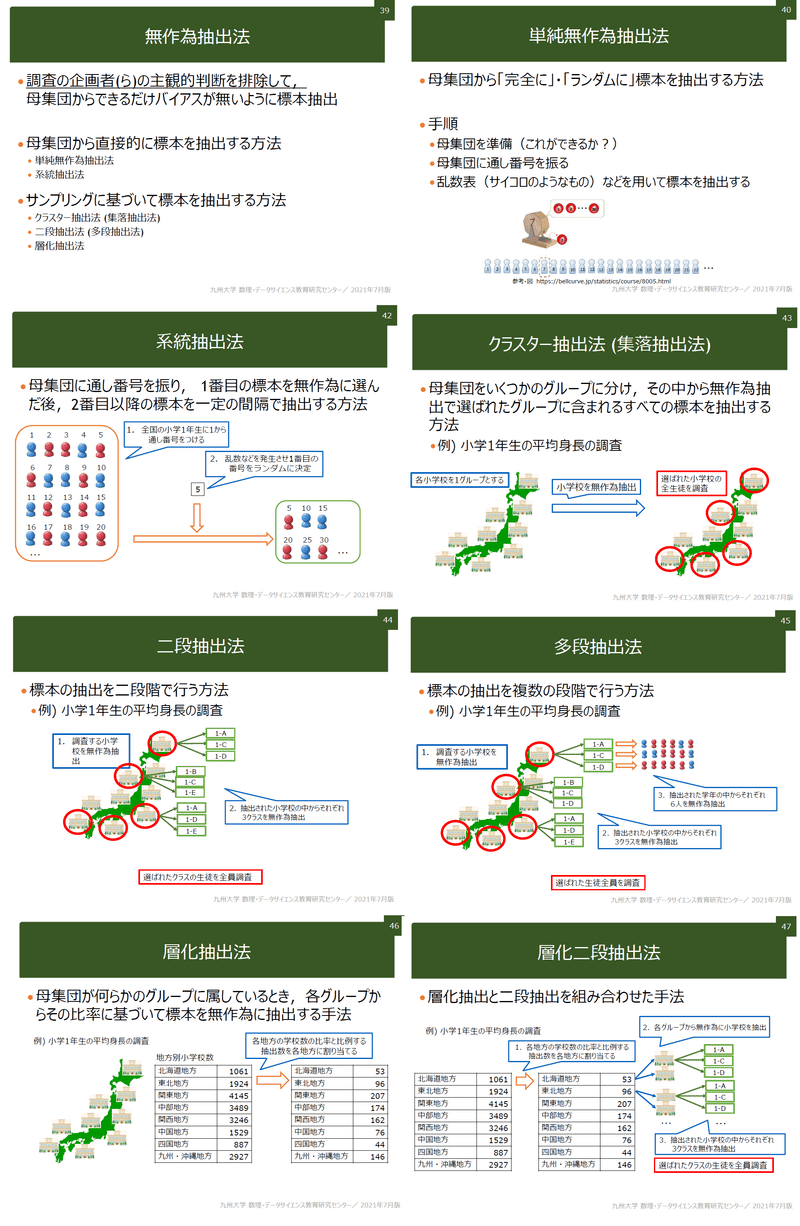
４－３．有意抽出法

　バイアスがかかる抽出法のため統計的な判断は基本的にはできない（いわゆるダメなサンプリング）。特にSNSでのアンケートなどはバイアスがかかりやすいため結果の判断には注意が必要です。

機縁法・縁故法
応募法
インターセプト法
割り当て法

５．オープンデータ

　サンプリング手法を学びましたが実際に実施すると時間もお金もかかります。既にあるデータの正しさを判断（無作為抽出か？バイアスがないか？標本数は十分かなど）したうえで、既にデータがあるならばそれを活用した方が効率的です。
　公共データとして公開されている情報がありオープンデータと呼びます。

５－１．オープンデータとは

　詳細は下記の通りです。

５－２．参考用サイト

https://dashboard.e-stat.go.jp/

キーワード一覧

カール・ピアソンの確率分布：ピアソンの論文「進化の数学理論への貢献1）」で紹介された確率分布
推測統計：母集団から抽出した標本の情報を用いて、母集団の情報を推測する。統計学的に推測するには、データに当てはまるであろう確率分布を推定し、その確率分布を基に、母集団のデータを推測します。
大数の法則（law of large numbers）：ある独立した試行においてその事象が発生する確率をpとすると、試行回数nが大きくなるにつれて事象の発生確率がpに近づいていくこと
中心極限定理：母集団が正規分布でなくても、そこから抽出したサンプルサイズNが大きくなると標本の分布は正規分布に近づく
モンテカルロ法：、乱数を用いた試行を繰り返すことにより近似解を求める手法->大数の法則を考慮すると試行回数nを大きくして近似解を取得
標準誤差(SE：standard error)：標本から測定された統計量の標準偏差であり標本統計量の精度を表す。標本平均の標準偏差を指すことが多い。

$$
不偏分散\sigma^2 = \frac{1}{n-1}\sum_{i=1}^{n} (x_i - \bar{x})^2
$$

$$
標準偏差\sigma = \sqrt{\sigma^2}
$$

$$
SE = \frac{\sigma}{\sqrt{n}}= \frac{\sqrt{不偏分散\sigma^2}}{\sqrt{n}}= \frac{\sqrt{\frac{1}{n-1} \displaystyle\sum^{n}_{i=1} (x_{i} - \bar{x})^{2}}} {\sqrt{n}}
$$

参考資料

あとがき

　追って追記予定

この記事が気に入ったらサポートをしてみませんか？