第８章「傾いた文字は正しい文字か？鏡文字か？」のベイズモデリングをPyMC Ver.5 で

2023年12月2日 11:03

この記事は、テキスト「たのしいベイズモデリング」の第８章「傾いた文字は正しい文字か？鏡文字か？」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。

この章では、通常の文字と左右逆さまの文字（鏡文字）を０～３６０度回転させて、回答者が通常の文字か鏡文字かを判断するのにかかった反応時間を混合プロセスモデルで分析します。

今回のモデルもかなり複雑であり、自己流PyMCモデルはテキストと大きく異なる結果を出力しました（３回連続の汗）
結果はさておき、楽しくPyMCでモデリングして、ベイズ推論を満喫しましょう！

テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。

テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。

サマリー

テキストの概要

執筆者　　　：　武藤拓之先生
モデル難易度：　★★★★★　（難しい）

自己評価

評点

$$
\begin{array}{c:c:c}
実装精度 & ★・・・・& 悪い \\
結果再現度 & ★・・・・& NG!! \\
楽しさ & ★★★★・& 楽しそう \\
\end{array}
$$

評価ポイント

モデルに含まれる「相関行列」（rho）に全く自信がないです。
- PyMCの「LKJCorr()」を使いこなせていません。
  確率変数的に利用するとサンプリング処理時にエラーが発生してしまいます。
- 今回はエラー回避の目的でモデル内で確定的な乱数を用いました。
  PyMCで一様な相関行列をモデル内で定義する方法が知りたいです。
- ひとまずこの記事のPyMCモデルは「PyMCの実装」の失敗例としてご活用下さい（泣）
とにかく$${\hat{R}}$$が非常に悪いです。収束できないです（泣）

工夫・喜び・反省

「指数－正規分布」と「多変量正規分布」のあわせ技（階層化）が面白かったです。
５つの潜在的変数の「個人別と全平均とマリアージュ」をお楽しみ下さい！

モデルの概要

テキストの調査・実験の概要

文字の心的回転処理のイメージ図です。
文字を見てから回答までの反応時間をコンピューターで計測しています。

■回転プロセスと非回転プロセス
図の例では文字が逆さになっていて、頭の中で回転処理をする人が多いかもしれません。
この回転処理をテキストでは「回転プロセス」と呼んでいます。
一方で、文字の傾きが小さい場合、わざわざ回転させなくても文字を判別できるでしょう。
このように回転させないで文字を判別する処理をテキストでは「非回転プロセス」と呼んでいます。

■混合プロセスモデル
２つのプロセスは反応時間にかかわります。
回転プロセスを経る場合、反応時間は長くなる可能性が高く、一方で非回転プロセスの場合、反応時間は短くなる可能性が高いのです。
「混合プロセスモデル」は、文字の向きと反応時間の対応関係に「回転プロセス」と「非回転プロセス」が混合して影響していると仮定するモデルです。
テキストに５つの仮定が記載されています。

テキストのモデリング

■目的変数と関心のあるパラメータ
目的変数$${RT}$$は反応時間（ミリ秒）です。
関心のあるパラメータは次の５つのパラメータです。
最初の３つは混合プロセスのパラメータ、残りの２つは反応時間が従うと仮定する指数－正規分布のパラメータです。

$${base}$$：基本的な処理に要する時間
$${rate}$$：心的に文字を１°回転させるのに要する時間
$${expo}$$：文字の回転の増大に伴う２つのプロセスの混合率の増加を表現
$${\sigma}$$：指数－正規分布の標準偏差パラメータ
$${\lambda}$$：指数－正規分布の平均生起回数パラメータ

■混合プロセスモデル
回転プロセスと非回転プロセスの混合モデルは整理されるとあっさりした数式になります。
$${\widehat{RT}}$$は反応時間の予測値、$${Angle}$$は文字の回転角度、添字$${i}$$は実験参加者のIDです。
この数式に至る検討過程はテキストでご確認下さい。

$$
\widehat{RT}_i = base_i + rate_i \times Angle \times \left( \cfrac{Angle}{180^{\circ}}\right)^{expo_i}
$$

テキストを一部改変して引用

■指数－正規分布モデル
反応時間は一般的には正規分布に従わず、フィッティングによく用いられる理論分布が「指数－正規分布」だそうです。
正規分布のパラメータ$${\sigma}$$と指数分布のパラメータ$${\lambda}$$によって反応時間データに含まれるノイズを表現します。

$$
RT \sim \text{ExpModNormal}\ (\ \widehat{RT}_i,\ \sigma_i,\ \lambda_i\ )
$$

テキストを一部改変して引用

■階層ベイズモデル
５つのパラメータの実験参加者の個人差が正規分布に従うと仮定しています。
個人ごとのパラメータをベクトル$${\boldsymbol{local}_i}$$で表現しています。

$$
\begin{align*}
\{ base_i, rate_i, \log expo_i, \sigma_i, \log \lambda_i \} &= \boldsymbol{local}_i \\
\boldsymbol{local}_i &\sim \text{MultiNormal}\ (\boldsymbol{\mu},\ \boldsymbol{cov}) \\
\boldsymbol{\mu} &= \{ \overline{base},\ \overline{rate},\ \log \overline{expo},\ \overline{\sigma},\ \log \overline{\lambda} \} \\
\boldsymbol{cov} &= \left[
\begin{matrix}
S_{11} &\cdots &S_{15} \\ \vdots &\ddots &\vdots \\ S_{51} &\cdots &S_{55} \\
\end{matrix}
\right]
\end{align*}
$$

テキストを一部改変して引用

$${\text{MultiNormal}}$$は多変量正規分布です。
多変量正規分布のパラメータのうち、ベクトル$${\boldsymbol{\mu}}$$は５つのパラメータの平均、行列$${\boldsymbol{cov}}$$は５つのパラメータの分散共分散行列です。

■事前分布
先行研究より$${\log \overline{expo} \cong 1.00}$$であることがわかっているとのことで、標準正規分布を弱情報事前分布としています、
その他のパラメータの事前分布については、テキストでは言及されておらず、Stanスクリプトにある程度記述されています。

$$
\log \overline{expo} \sim \text{Normal}(0, 1)
$$

テキストより引用

■分析・分析結果
分析結果はテキストに記載の図表を利用して実施して下さい。
PyMCの自己流モデルはテキストと異なる結果となってしまい、分布は収束せず、分析に利用できない状況です（スミマセン・・・）。

PyMC実装

Let's enjoy PyMC & Python !

準備・データ確認

１．インポート

### インポート

# ユーティリティ
import pickle

# 数値・確率計算
import pandas as pd
import numpy as np

# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

２．データの読み込み
csvファイルをpandasのデータフレームに読み込みます。

### データの読み込み
data_orgn = pd.read_csv('data.csv')
display(data_orgn)

【実行結果】
モデリングで利用する項目は以下のとおりです。
・ID：実験参加者のID　※説明変数
・RotAngle：文字の回転角度（最短角距離：0～180°）　※説明変数
・RT：反応時間　※目的変数
ダウンロードファイルに項目説明ファイルが含まれています。

データの前処理をします。
Rスクリプトの処理と同じ内容の前処理にしました。

### データの前処理 ★Rコードに準拠
# データコピー
data = data_orgn.copy()
# 不正解試行の除外
data = data[data['Err']==0]
# 外れ値試行の除外 有効反応時間 200ms<=RT<=5000ms
data = data[(data['RT'] >= 200) & (data['RT'] <= 5000)].reset_index(drop=True)
# データの表示
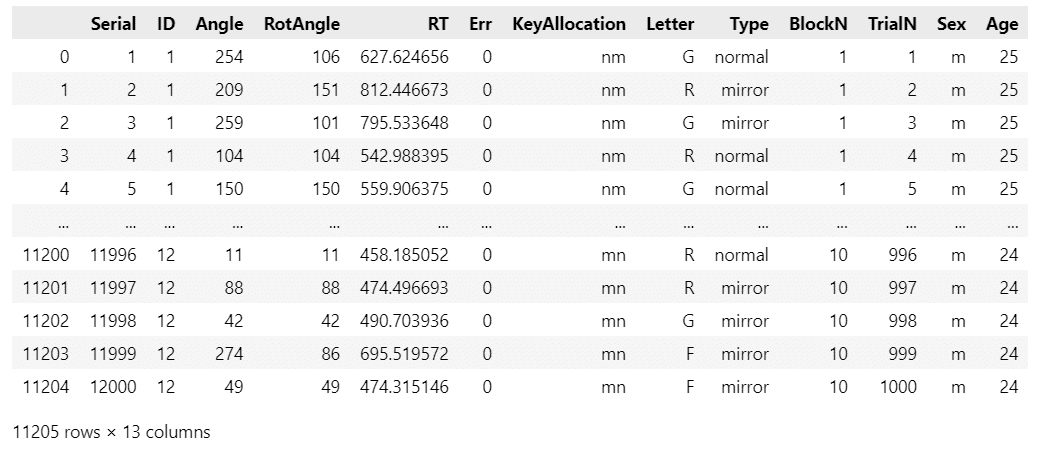
display(data)

【実行結果】
データ件数は11205件となりました。

３．データの外観・統計量

ひとまず要約統計量を確認します。

### 要約統計量の表示
data.describe().round(2)

【実行結果】

文字タイプごとに文字の傾きと反応時間（平均値）をグラフにしてみましょう。

### 文字の傾きと平均反応時間の描画

## データの準備
# 平均反応時間
means = data.groupby(['Letter', 'Type', 'Angle'])['RT'].mean().reset_index()
# 文字のリスト
letters = means['Letter'].unique()
# タイプ（通常の文字か鏡文字か）のリスト
types = ['normal', 'mirror']

## 描画
fig, ax = plt.subplots(3, 1, figsize=(8, 8), sharey=True)
# 文字ごとに描画
for i, l in enumerate(letters):
    # タイプごとに線の色を変えて折れ線グラフを描画
    for t in types:
        # 文字・タイプで絞り込み
        tmp = means[(means['Letter']==l) & (means['Type']==t)]
        # 描画
        ax[i].plot(tmp['Angle'], tmp['RT'], lw=1, label=f'{t}')
    # axes単位の修飾
    # ax[i].set_ylim(500, 1500)
    ax[i].set_xticks(np.linspace(0, 360, 7))
    ax[i].set_title(f'文字:{l}')
    ax[i].legend(loc='upper left')

# 全体の修飾
fig.suptitle('文字の傾きと平均反応時間')
fig.supxlabel('文字の向き（度）')
fig.supylabel('反応時間（ミリ秒）')
plt.tight_layout()
plt.show()

【実行結果】
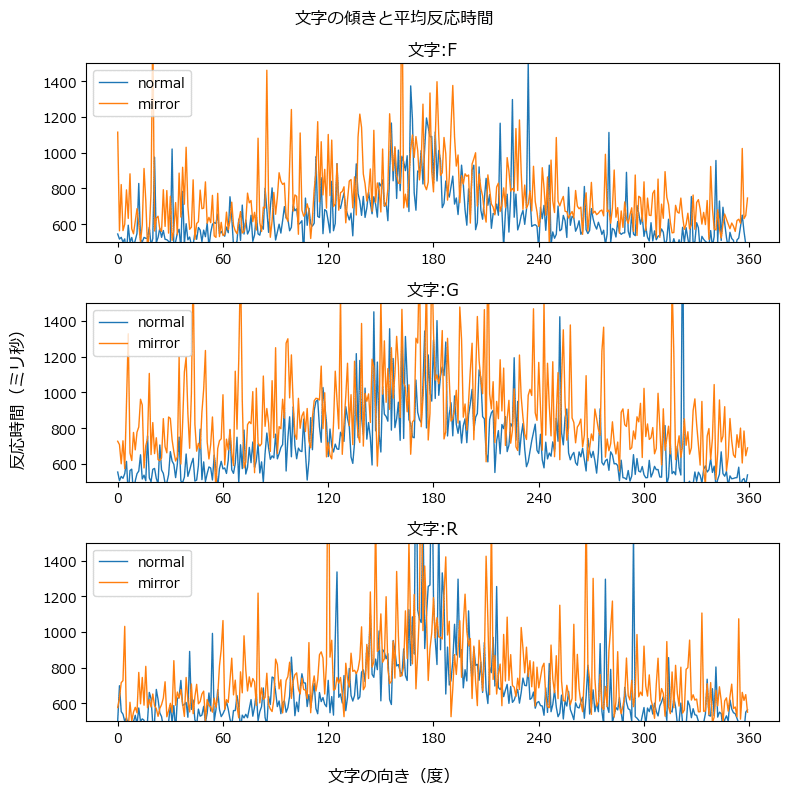
２つのグラフを作成しました。
上側が全ての反応時間、下側が500～1500秒の反応時間です。
下側の方が傾向をつかみやすいかもです。

青色の正しい文字は180°を尖った頂点にして急カーブの曲線を描いている感じがします。
オレンジ色の鏡文字は青色の線と傾向は似ていますが、大きなノイズが含まれている感じがします。

モデルの実装

階層ベイズモデルの実装です。
事後分布からのサンプリング結果がテキストと大きく相違します。
PyMCモデリングの参考例くらいのゆるい見方をお願いします。

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
テキストおよびStanコードに沿った形です。
長くなってしまいました・・・。

$$
\begin{align*}
\mu_{base} &\sim \text{Uniform}\ (\text{lower}=200,\ \text{upper}=1000) \\
\mu_{rate} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=3) \\
\mu_{\log expo} &\sim \text{TruncatedNormal}\ (\text{mu}=0,\ \text{sigma}=1, \text{lower}=-2,\ \text{upper}=2) \\
\mu_{\sigma} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=60) \\
\mu_{\log \lambda} &\sim \text{Uniform}\ (\text{lower}=-6.5,\ \text{upper}=-4.0) \\
mus &= \{\mu_{base},\ \mu_{rate},\ \mu_{\log expo},\ \mu_{\sigma},\ \mu_{\log \lambda}\}\\
\sigma_{base} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\sigma_{rate} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=10) \\
\sigma_{\log expo} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=3) \\
\sigma_{\sigma} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\sigma_{\log \lambda} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=1.5) \\
\rho\_matrix &= corr\_matrix(\text{LKJCorr}(\text{n}=5,\ \text{eta}=1))\\
\sigma\_diag &= diag_matrix(\sigma_{base},\ \sigma_{rate},\ \sigma_{\log expo},\ \sigma_{\sigma},\ \sigma_{\log \lambda})\\
cov\_matrix &= \sigma\_diag\ @\ \rho\_matrix\ @\ \sigma\_diag \\
local_i &\sim \text{MvNormal}\ (\text{mu}=mus,\ \text{cov}=cov\_matrix)\\
\{base_i, rate_i, \log expo_i, \sigma_i, \log \lambda_i\} &= local_i \\
expo_i &= \exp (\log expo_i)\\
\lambda_i &= \exp (\log \lambda_i) \\
\widehat{RT}_i &= base_i + rate_i \times Angle \times \left( \cfrac{Angle}{180^{\circ}}\right)^{expo_i}\\
likelihood &= \text{ExNormal}\ (\text{mu}=\widehat{RT}_i,\ \text{sigma}=\sigma_i,\ \text{nu}=1 / \lambda_i) \\
\end{align*}
$$

式中の妄想数式の意図は次のとおりです。

$${corr\_matrix}$$：$${\text{LKJCorr()}}$$で取得した上三角行列から相関行列を生成
$${diag\_matrix}$$：与えられたベクトルを対角成分に配置する対角行列を生成

１．モデルの定義
リスト・インデックス、coord、data、パラメータの事前分布、尤度、計算値をそれぞれ定義・指定します。
id_idxは説明変数IDの値から1を差引いたインデックスです。

### モデルの定義

### リスト・インデックスの作成
# 実験参加者のIDのリストとインデックスの作成
id_list = list(set(data['ID']))
id_idx = data['ID'].values - 1
# ５つのlocalパラメータのリストの作成
params_list = ['base', 'rate', 'logExpo', 'σ', 'logλ']

### モデルの定義
with pm.Model() as model:

    ### データ関連定義
    # coordの定義
    model.add_coord('data', values=data.index, mutable=True)
    model.add_coord('ID', values=id_list, mutable=True)           # 実験参加者ID
    model.add_coord('params', values=params_list, mutable=True)   # 5つのparam
    # dataの定義
    RT = pm.ConstantData('RT', value=data['RT'], dims='data')
    angle = pm.ConstantData('angle', value=data['RotAngle'], dims='data')
    idIdx = pm.ConstantData('idIdx', value=id_idx, dims='data')

    ### パラメータの事前分布
    # base, rate, log expo, sigma, log lambdaの平均と標準偏差の事前分布
    muBase = pm.Uniform('muBase', lower=200, upper=1000)
    muRate = pm.Uniform('muRate', lower=0, upper=3)
    muLogExpo = pm.TruncatedNormal('muLogExpo', mu=0, sigma=1, lower=-2, upper=2)
    muSigma = pm.Uniform('muSigma', lower=0, upper=60)
    muLogLam = pm.Uniform('muLogLam', lower=-6.5, upper=-4.0)
    sigmaBase = pm.Uniform('sigmaBase', lower=0, upper=100)
    sigmaRate = pm.Uniform('sigmaRate', lower=0, upper=10)
    sigmaLogExpo = pm.Uniform('sigmaLogExpo', lower=0, upper=3)
    sigmaSigma = pm.Uniform('sigmaSigma', lower=0, upper=100)
    sigmaLogLam = pm.Uniform('sigmaLogLam', lower=0, upper=1.5)
    
    #### local関連定義
    ### local の平均ベクトルパラメータmusの作成
    mus = pt.stack([muBase, muRate, muLogExpo, muSigma, muLogLam])
    
    ### local の共分散行列パラメータcovMatrixの作成
    ## 相関行列rhoの事前分布 ※pytensorのソースを引用
    # 初期値設定：行数とshape
    n = len(params_list)
    shape = n * (n - 1) // 2
    # 上三角行列のインデックス作成
    tri_index = np.zeros((n, n), dtype="int32")
    tri_index[np.triu_indices(n, k=1)] = np.arange(shape)
    tri_index[np.triu_indices(n, k=1)[::-1]] = np.arange(shape)
    # rhoの事前分布：LKJCorrの戻り値は上三角行列要素の１次元配列
    # rho = pm.LKJCorr('rho', n=n, eta=1)        # ★エラーが発生する
    # rho = pm.LKJCorr.dist(n=n, eta=1)          # ★エラーが発生する
    rho = pm.draw(pm.LKJCorr.dist(n=n, eta=1))   # ★エラー回避できるが確率変数にならない
    # 行列化：上三角行列インデックスにrhoを当てはめて、対角要素に1を設定
    rhoMatrix = pm.Deterministic('rhoMatrix',
                                 pt.fill_diagonal(pt.take(rho, tri_index), 1))
    ## 標準偏差の対角行列化
    # 標準偏差をベクトル化
    sigmas = pt.stack([sigmaBase, sigmaRate, sigmaLogExpo, sigmaSigma,
                       sigmaLogLam])
    # 標準偏差を対角行列化
    sigmaDiag = pt.basic.alloc_diag(sigmas)
    ## 分散共分散行列の作成
    covMatrix = pm.Deterministic('covMatrix',
                                 pt.dot(pt.dot(sigmaDiag, rhoMatrix),
                                        sigmaDiag))

    ### localの事前分布: 多変量正規分布
    local = pm.MvNormal('local', mu=mus, cov=covMatrix, dims=('ID', 'params'))
    
    #### 尤度の定義
    # 実験参加者ごとの５つのパラメータをlocalから分離
    base = pm.Deterministic('base', local[:, 0], dims='ID')
    rate = pm.Deterministic('rate', local[:, 1], dims='ID')
    logExpo = pm.Deterministic('logExpo', local[:, 2], dims='ID')
    sigma = pm.Deterministic('sigma', local[:, 3], dims='ID')
    logLam = pm.Deterministic('logLam', local[:, 4], dims='ID')
    # 対数をもとに戻す
    expo = pm.Deterministic('expo', pt.exp(logExpo), dims='ID')
    lam = pm.Deterministic('lam', pt.exp(logLam), dims='ID')
    # 反応時間RTの予測値rtPredの算出
    rtPred = pm.Deterministic(
            'rtPred',
            base[idIdx] + rate[idIdx] * angle * pt.pow((angle/180), expo[idIdx]),
            dims='data')
    
    ## 尤度：指数－正規分布　観測値:反応時間RT
    likelihood = pm.ExGaussian('likelihood', mu=rtPred, sigma=sigma[idIdx],
                               nu=1 / lam[idIdx], observed=RT, dims='data')
    
    ### 計算値
    muExpo = pm.Deterministic('muExpo', pt.mean(expo))
    muLam = pm.Deterministic('muLam', pt.mean(lam))
    muLamReciprocal = pm.Deterministic('muLamReciprocal', 1 / pt.mean(lam))

【モデル注釈】

coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次を設定しました
- 行の座標：名前「data」、値「行インデックス」
- 実験参加者のIDの座標：名前「ID」、値「ID」
- パラメータの座標：名前「params」、値「param_list」（5個）
dataの定義
目的変数$${RT}$$：反応時間、説明変数$${angle}$$（RotAngle）、説明変数$${idIdx}$$（IDのインデックス）を設定しました。
パラメータの事前分布
- モデルの数式表現のとおりに設定しました。
- テキスト・Stanスクリプトに無いパラメータ値は適当に設定しました。
- 相関行列の素「rho」には注意が必要です。
  テキストにならって、パラメータeta=1の一様な相関行列を作成したいのですが、うまく定義できない部分になりました。
  - PyMCのLKJCorrは上三角行列（n=5の場合、要素10個）を生成します。
  - 次を設定すると、サンプリング処理時にエラーが発生します。
    次元／形状がうまくマッチしない感じのエラーです。
    - rho = pm.LKJCorr('rho', n=n, eta=1)
    - rho = pm.LKJCorr.dist(n=n, eta=1)
  - エラー回避のためやむを得ず、pm.draw()を用いてrhoに確定した乱数を設定することにしました。
- localは多変量正規分布 MvNormalです。
尤度
指数－正規分布ExGaussianです。次元は「data」です。

【2023/12/05追記】
相関行列「rho」の計算に LKJCholeskyCov() を用いたモデルを作成しました。
詳細は「モデルの実装（改）」の項をご覧ください。

２．モデルの外観の確認

### モデルの表示
model

【実行結果】
localが従う多変量正規分布のパラメータが長ーーーいです🐘

### モデルの可視化
pm.model_to_graphviz(model)

【実行結果】
巨大なグラフになりました。
localをハブにして、集まって放出される「m : 1」「1 : n」の関係が面白いです（正しくモデリングできているか不安です）。

３．事後分布からのサンプリング
乱数生成数については、drawsはRスクリプトの数に合わせました。
tune（バーンイン期間）は収束を目指してテキストよりもかなり増やしています。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ90秒でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 90秒
with model:
    idata = pm.sample(draws=4000, tune=10000, chains=4, target_accept=0.95, 
                      nuts_sampler='numpyro', random_seed=999)

【実行結果】省略

４．サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。

### r_hat>1.1の確認
rhat_idata = az.rhat(idata)
(rhat_idata > 1.1).sum()

【実行結果】
全パラメータが収束していません！

📢 分析断念のお知らせ 📢
収束させることができないため、ベイズ推論による分析ができません。
ここからは、Pythonコードの参考例の位置づけで続行します。
※ExGaussian() の使い方とテキストの指数－正規分布が合っていないような気がしています。

パラメータ等の事後分布の要約統計量です。
パラメータ種が多いので、分割して、かつ、限定的に選んで、確認します。

var_names = ['muBase', 'muRate', 'muExpo', 'muSigma', 'muLamReciprocal']
pm.summary(idata, hdi_prob=0.95, var_names=var_names)

【実行結果】

var_names = ['sigmaBase', 'sigmaRate', 'sigmaLogExpo', 'sigmaSigma', 'sigmaLogLam']
pm.summary(idata, hdi_prob=0.95, var_names=var_names)

【実行結果】

トレースプロットを確認しましょう。

pm.plot_trace(idata, combined=True, var_names=['muBase', 'muRate', 'muLogExpo',
                                               'muSigma', 'muLogLam'])
plt.tight_layout();

【実行結果】
複数の峰が出現しています。

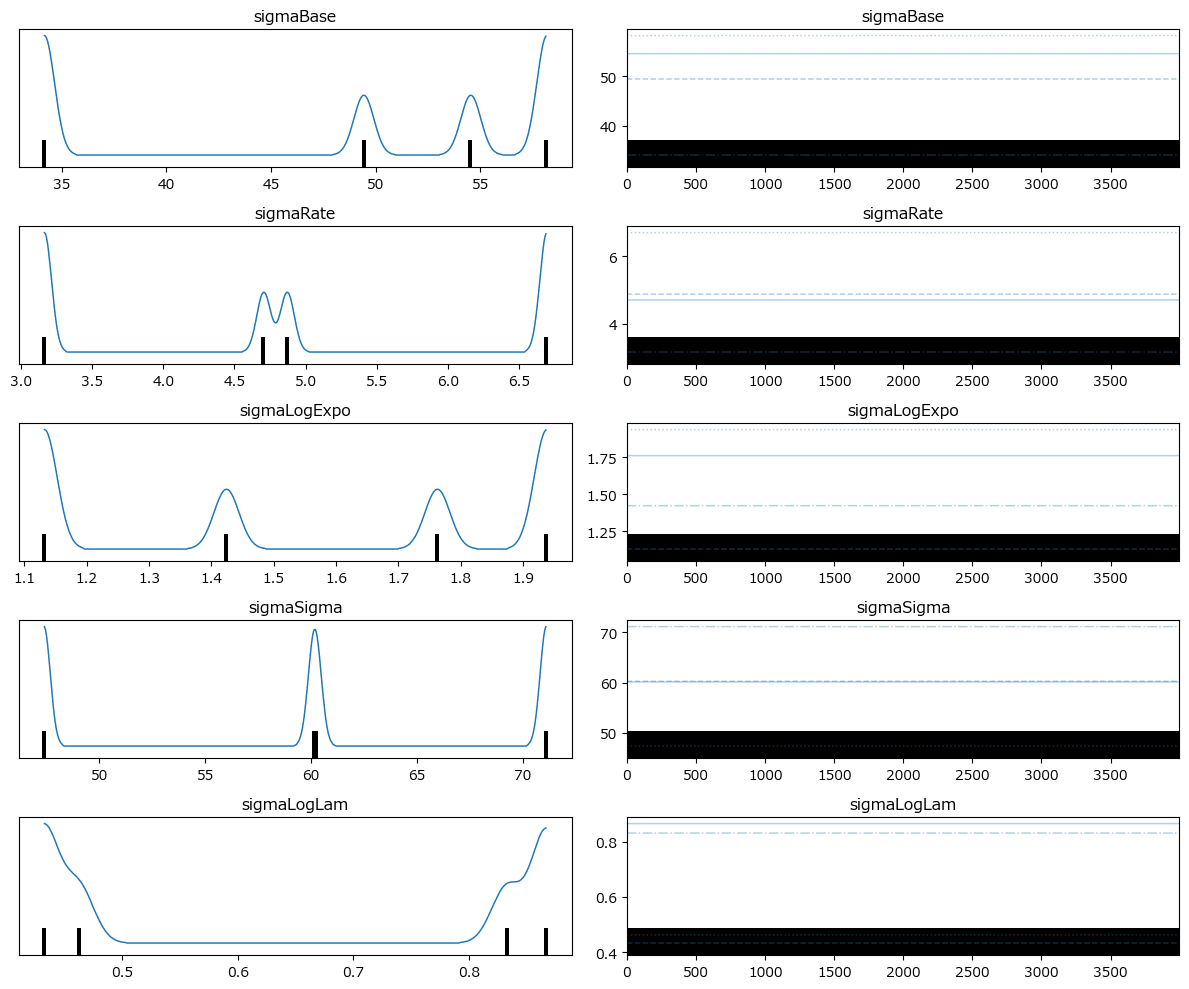
pm.plot_trace(idata, combined=True, var_names=['sigmaBase', 'sigmaRate',
                                'sigmaLogExpo', 'sigmaSigma', 'sigmaLogLam'])
plt.tight_layout();

【実行結果】
複数の峰が出現しています。

５．分析～テキストにならって

テキスト表8.1の要約統計量の代替コードです。
MAPに代えてEAP（平均値）を使用しました。

### 集団レベルのパラメータの事後分布に関する要約統計量（EAPと95%HDI）
# ★テキストの表8.1に対応

# 初期値設定
val_list = ['muBase', 'muRate','muExpo', 'muSigma', 'muLamReciprocal',
            'sigmaBase', 'sigmaRate','sigmaLogExpo', 'sigmaSigma', 'sigmaLogLam']
col_list = ['base', 'rate', 'expo', 'σ', '1/λ', 'σbase', 'σrate', 'σlog_expo',
            'σσ', 'σlog_λ']
# 95%HDIの計算
hdi_data = pm.hdi(idata, hdi_prob=0.95)

# データフレーム化
df = pd.DataFrame()
for (val, col) in zip(val_list, col_list):
    # リストの各項目のEAP（平均）・95%HDI・標準偏差をデータフレームに追加
    tmp = pd.DataFrame(
        {col: [idata.posterior[val].mean().data, hdi_data[val][0].data,
               hdi_data[val][1].data, idata.posterior[val].std()]}
    )
    df = pd.concat([df, tmp], axis=1)
# データフレームの調整（列名の変更、型の変更）
df = df.T.rename(columns={0: 'EAP', 1: '2.5%',2: '97.5%', 3: 'std'}
                ).astype(float)
# データフレームの表示
df.round(2)

【実行結果】
上５つが参加者間平均値、下５つが参加者間標準偏差（個人の差の程度）です。
収束していないので、この表の数値を利用して分析することはできません。。。

６．推論データ（idata）の保存
推論データを再利用することはないと思いますが、ひとまずファイルに保存しましょう。
idataをpickleで保存します。

### idataの保存 pickle
file = r'idata_ch08.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata_ch08.pkl'
with open(file, 'rb') as f:
    idata_load = pickle.load(f)

モデルの実装（改）

【2023/12/05追記】
相関行列「rho」の計算に LKJCholeskyCov() を用いたモデルを作成しました。

１．モデルの定義

### モデルの定義

### リスト・インデックスの作成
# 実験参加者のIDのリストとインデックスの作成
id_list = list(set(data['ID']))
id_idx = data['ID'].values - 1
# ５つのlocalパラメータのリストの作成
params_list = ['base', 'rate', 'logExpo', 'σ', 'logλ']

### モデルの定義
with pm.Model() as model:

    ### データ関連定義
    # coordの定義
    model.add_coord('data', values=data.index, mutable=True)
    model.add_coord('ID', values=id_list, mutable=True)           # 実験参加者ID
    model.add_coord('params', values=params_list, mutable=True)   # 5つのparam
    # dataの定義
    RT = pm.ConstantData('RT', value=data['RT'], dims='data')
    angle = pm.ConstantData('angle', value=data['RotAngle'], dims='data')
    idIdx = pm.ConstantData('idIdx', value=id_idx, dims='data')

    ### パラメータの事前分布
    # base, rate, log expo, sigma, log lambdaの平均と標準偏差の事前分布
    muBase = pm.Uniform('muBase', lower=200, upper=1000)
    muRate = pm.Uniform('muRate', lower=0, upper=3)
    muLogExpo = pm.TruncatedNormal('muLogExpo', mu=0, sigma=1, lower=-2, upper=2)
    muSigma = pm.Uniform('muSigma', lower=0, upper=60)
    muLogLam = pm.Uniform('muLogLam', lower=-6.5, upper=-4.0)
    sigmaBase = pm.Uniform('sigmaBase', lower=0, upper=100)
    sigmaRate = pm.Uniform('sigmaRate', lower=0, upper=10)
    sigmaLogExpo = pm.Uniform('sigmaLogExpo', lower=0, upper=3)
    sigmaSigma = pm.Uniform('sigmaSigma', lower=0, upper=100)
    sigmaLogLam = pm.Uniform('sigmaLogLam', lower=0, upper=1.5)
    
    #### local関連定義
    ### local の平均ベクトルパラメータmusの作成
    mus = pt.stack([muBase, muRate, muLogExpo, muSigma, muLogLam])
    
    ### local の共分散行列パラメータcovMatrixの作成
    ## 相関行列rho
    # 初期値設定：行数とshape
    n = len(params_list)
    # LKJCholesky共分散に用いる標準偏差の分布
    sd_dist = pm.Uniform.dist(lower=0, upper=100, size=n)
    # LKJCholesky共分散にて相関行列を取得
    _, rho, _ = pm.LKJCholeskyCov('rho', eta=1, n=n, sd_dist=sd_dist,
                                  compute_corr=True)
    ## 標準偏差の対角行列化
    # 標準偏差をベクトル化
    sigmas = pt.stack([sigmaBase, sigmaRate, sigmaLogExpo, sigmaSigma,
                       sigmaLogLam])
    # 標準偏差を対角行列化
    sigmaDiag = pt.basic.alloc_diag(sigmas)
    ## 分散共分散行列の作成
    covMatrix = pm.Deterministic('covMatrix',
                                 pt.dot(pt.dot(sigmaDiag, rho), sigmaDiag))

    ### localの事前分布: 多変量正規分布
    local = pm.MvNormal('local', mu=mus, cov=covMatrix, dims=('ID', 'params'))
    
    #### 尤度の定義
    # 実験参加者ごとの５つのパラメータをlocalから分離
    base = pm.Deterministic('base', local[:, 0], dims='ID')
    rate = pm.Deterministic('rate', local[:, 1], dims='ID')
    logExpo = pm.Deterministic('logExpo', local[:, 2], dims='ID')
    sigma = pm.Deterministic('sigma', local[:, 3], dims='ID')
    logLam = pm.Deterministic('logLam', local[:, 4], dims='ID')
    # 対数をもとに戻す
    expo = pm.Deterministic('expo', pt.exp(logExpo), dims='ID')
    lam = pm.Deterministic('lam', pt.exp(logLam), dims='ID')
    # 反応時間RTの予測値rtPredの算出
    rtPred = pm.Deterministic(
            'rtPred',
            base[idIdx] + rate[idIdx] * angle * pt.pow((angle/180), expo[idIdx]),
            dims='data')
    
    ## 尤度：指数－正規分布　観測値:反応時間RT
    likelihood = pm.ExGaussian('likelihood', mu=rtPred, sigma=sigma[idIdx],
                               nu=1 / lam[idIdx], observed=RT, dims='data')
    
    ### 計算値
    muExpo = pm.Deterministic('muExpo', pt.mean(expo))
    muLam = pm.Deterministic('muLam', pt.mean(lam))
    muLamReciprocal = pm.Deterministic('muLamReciprocal', 1 / pt.mean(lam))

【モデル注釈】変更点

相関行列 rho
- pm.LKJCholeskyCov() を用いて相関行列 rho を算出しています。
- 引数
  - eta：1：一様分布（テキストとおそらく同様）
  - n：共分散行列の次元５
  - sd_dist：標準偏差の分布
  - compute_corr：True。相関行列と標準偏差を返す

相関行列の様子を見てみましょう。

# 相関行列の確認
rho.eval()

【実行結果】

２．モデルの外観の確認
LKJCholeskyCov() が生成する変数名にアンダースコアが含まれており、自環境で KeTex エラーが発生するため、別の方法でモデル式を表示します。

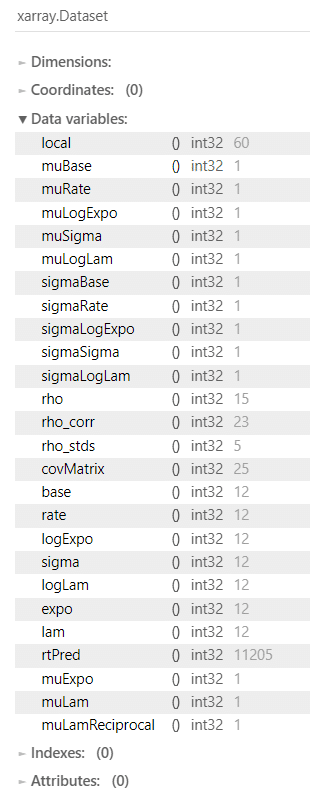
# モデルの表示：決定論的変数を含まない確率変数のリスト
model.basic_RVs

【実行結果】

# モデルの表示：決定論的変数を含む確率変数のリスト（観測値の変数は表示されない）
model.unobserved_RVs

【実行結果】

### モデルの可視化
pm.model_to_graphviz(model)

【実行結果】

３．事後分布からのサンプリング
乱数生成数については、drawsはRスクリプトの数に合わせました。
tune（バーンイン期間）は収束を目指してテキストよりもかなり増やしています。
また、target_accept の値も大きくしてみました。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ95秒でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 95秒
with model:
    idata = pm.sample(draws=4000, tune=10000, chains=4, target_accept=0.998, 
                      nuts_sampler='numpyro', random_seed=999)

【実行結果】省略

### r_hat>1.1の確認
rhat_idata = az.rhat(idata)
(rhat_idata > 1.1).sum()

【実行結果】
こちらもモデルも全パラメータが収束していません！
指数－正規分布をうまく使えていないかもしれません。

５．分析～テキストにならって

ひとまず、テキスト表8.1の要約統計量の表を作成してみましょう。
MAPに代えてEAP（平均値）を使用しました。

### 集団レベルのパラメータの事後分布に関する要約統計量（EAPと95%HDI）
# ★テキストの表8.1に対応

# 初期値設定
val_list = ['muBase', 'muRate','muExpo', 'muSigma', 'muLamReciprocal',
            'sigmaBase', 'sigmaRate','sigmaLogExpo', 'sigmaSigma', 'sigmaLogLam']
col_list = ['base', 'rate', 'expo', 'σ', '1/λ', 'σbase', 'σrate', 'σlog_expo',
            'σσ', 'σlog_λ']
# 95%HDIの計算
hdi_data = pm.hdi(idata, hdi_prob=0.95)

# データフレーム化
df = pd.DataFrame()
for (val, col) in zip(val_list, col_list):
    # リストの各項目のEAP（平均）・95%HDI・標準偏差をデータフレームに追加
    tmp = pd.DataFrame(
        {col: [idata.posterior[val].mean().data, hdi_data[val][0].data,
               hdi_data[val][1].data, idata.posterior[val].std()]}
    )
    df = pd.concat([df, tmp], axis=1)
# データフレームの調整（列名の変更、型の変更）
df = df.T.rename(columns={0: 'EAP', 1: '2.5%',2: '97.5%', 3: 'std'}
                ).astype(float)
# データフレームの表示
df.round(2)

【実行結果】
最初のモデルとほぼ同じ結果になりました。
ただし標準偏差（std）は、変数によって大きく変化したようです。

（参考：最初のモデルの要約統計量）

以上で第８章は終了です。
表8.2、図8.6は省略しました。

おわりに

鏡文字か、鏡餅か

人間の認知プロセスに切り込む認知心理学的なテーマでした。
予めベイズモデリングを定め、実験参加者から実験データを収集して、分析するという、一連のデータ分析過程を疑似体験できる素晴らしい章です。
がしかし、PyMC自己流モデルの限界を超えてしまい、事後分布（からの乱数）が収束することなく、BADエンディングを迎える結果になってしまいました。
残念です・・・。

とは言うものの、この章のモデルに取り組んだ当初は、サンプリング時のエラーが解消できず、「お蔵入り」候補だったのです。
エラー回避ができるようになったことだけでも喜んでおこうと思います！
やったー！

記事のアップデート

2023年12月10日にこの章のアップデート記事を投稿しました。
新記事では遂に分布が収束しました！
ぜひ新記事もお読み下さい。

シリーズの記事

次の記事

前の記事

ブログの紹介

note で４つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。

２．RとStanではじめる心理学のための時系列分析入門を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ（お題）を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます！
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀

３．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。

４．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。

最後までお読みいただきまして、ありがとうございました。

この記事が参加している募集

#お金について考える

39,070件

この記事が気に入ったらサポートをしてみませんか？