
第9章「己の歌唱力を推定する」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング」の第9章「己の歌唱力を推定する」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
この章では、カラオケ採点システムの上限値を超える「真の総合得点」を時系列のベイズモデルで推論します。

今回は3つのモデリングに挑戦します。
極めつけは3つ目の「状態空間モデル」です。
しかし今回もまたまた、自己流PyMCモデルはテキストと大きく異なる結果を出力しました(4回連続の汗)
結果はさておき、楽しくPyMCでモデリングして、ベイズ推論を満喫しましょう!
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 紀ノ定保礼 先生
モデル難易度: ★★★★★ (難しい)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★・・・& いまいち \\
結果再現度 & ★★・・・& やや悪い \\
楽しさ & ★★★★★& 楽しい! \\
\end{array}
$$

評価ポイント
執筆者による推論よりも低い点数になってしまいました。
先生、ごめんなさい!
私の実装精度と結果再現度の評価も低くしておきました!「状態空間モデル」に挑戦しました!楽しかったです!
状態空間モデルはPyMCの実験中の機能を提供する pymc_experimental に含まれています。簡単に将来予測できる優れものです!

工夫・喜び・反省
pymc_experimentalの状態空間モデルの構築に当たっては、「ぱぐみさん」のコードを使わせていただきました。
pymc_experimentalの状態空間モデルの日本語情報が少ない中、実際に動くコードを共有していただいています。
ありがとうございます!
モデルの概要
テキストの調査・実験の概要
■カラオケ採点システムの仕組み
カラオケの採点システムの総合得点は、基礎的な得点(素点)と何らかのアルゴリズムで算出されたボーナス点を合計して計算されます。
素点が95点、ボーナス点が3点の場合、総合得点は98点です。
ただし、総合得点の上限は100点と定められているため、例えば、素点が99点の場合、ボーナス点は最高1点までになるそうです。
ボーナス点を減らして調整していると考えられています。
執筆者は、調整前(減らす前)のボーナス点と素点の合計を「真の総合得点」と呼んでいます。
調整前のボーナス点が2点で素点が99点の場合、真の総合得点は101点です。
■真の総合得点をベイズします
しかし、真の総合得点はカラオケ採点システムでは表示されません。
ということで、執筆者はベイズモデルを用いて、真の総合得点を推論したのです!
100点を連発できるって、とても羨ましいです。
テキストでは、試行6回の「曲H」と試行30回「曲S」を用いて、真の総合得点を推論を実践しています。
HとSのタイトル、気になりますね!

テキストのモデリング
1.曲「H」
■目的変数と関心のあるパラメータ
目的変数$${y}$$は総合得点です。
関心のあるのはもちろん「真の総合得点」です。
テキストでは2つのモデルで「真の総合得点」の推論を試みます。
■1つ目のモデル「打ち切られていないデータで推論」
試行回数7回のうち、最初の6回は100点未満のため、ボーナス点の調整は行われていません。
この6回の試行データを用いて、総合得点$${y_n}$$を推論します。
$$
\begin{align*}
y_n &\sim \text{Normal}\ (\mu,\ \sigma),\quad n=1, \cdots, 6 \\
y_{cens} &\sim \text{Normal}\ (\mu,\ \sigma)[100,\ +\infty] \\
\end{align*}
$$
$${y_n}$$は平均$${\mu}$$、標準偏差$${\sigma}$$の正規分布に従うと仮定しています。
また、同じ平均$${\mu}$$、標準偏差$${\sigma}$$を用いて、下限100の切断正規分布に従う「真の総合得点」$${y_{cens}}$$を推論します。
なお、$${\mu,\ \sigma}$$の事前分布は明示されていません。

■2つ目のモデル「打ち切りデータを活用して推論」
打ち切りのない試行6回のデータが従う確率分布と、打ち切りされた試行1回のデータが従う確率の両方を定義するモデルです。
$$
\begin{align*}
y_n &\sim \text{Normal}\ (\mu,\ \sigma),\quad n=1, \cdots, 6 \\
\text{Pr}[y>U] &= \int^{\infty}_U \text{Normal}\ (y \mid \mu,\ \sigma) dy=1-\phi \left( \cfrac{y-\mu}{\sigma}\right) \\
\end{align*}
$$
上式が打ち切りのない試行、下式が打ち切りされた試行に対応します。
$${U}$$は打ち切り点(100)、$${\phi(\ )}$$は標準正規分布の累積分布関数です。
なお、$${\mu,\ \sigma}$$の事前分布は明示されていません。
2.曲「S」
■ローカル・レベル・モデル
ローカル・レベル・モデルは、時系列的な変化を考慮した状態空間モデルの一種です。
「真の状態」を$${\mu}$$と表すと、ローカル・レベル・モデルでは$${\mu}$$が試行ごとに変化することを認めるとのこと。
学習や疲労などによって試行ごとに真の歌唱力が変動する(してしまう)ことをモデルに反映できるようです。
$$
\begin{align*}
y_t &\sim \text{Normal}\ (\mu_t,\ \sigma_{\epsilon}) \\
\mu_t &\sim \text{Normal}\ (\mu_{t-1}, \sigma_{\xi}) \\
\xi_t &\sim \text{Normal}\ (0,\ \sigma_{\xi}) \\
\mu_t &= \mu_{t-1} + \xi_{t-1}, \quad t=2, \cdots, 30 \\
\end{align*}
$$
ざっくり「1回前の実力が今回の得点力のベースになるけど、不確定要素も加味するよ!」ってことです!
試行$${t}$$の真の歌唱力$${\mu_t}$$は、直前の試行$${t-1}$$における真の歌唱力$${\mu_{t-1}}$$と誤差$${\xi_{t-1}}$$の足し合わせとして表現されています。
また、真の歌唱力$${\mu_t}$$と誤差$${\epsilon_t}$$(マイクの調子が悪いなど)による正規分布に従って、総合得点$${y_t}$$が立ち上ります。

■目的変数と関心のあるパラメータ
目的変数$${y}$$は総合得点です。
関心のあるのは「31回めの試行の真の総合得点」の予測です。
事前分布はStanスクリプトに次のように定義されています。
$$
\mu \sim \text{Normal}\ (0,\ 100) \\
\sigma_{\xi},\ \sigma_{\epsilon} \sim \text{StudentT} \ (3,\ 0,\ 100) \\
$$
$${\mu}$$はおそらく試行1回目の$${\mu_1}$$に関わる事前分布と思われます。
■分析・分析結果
分析結果はテキストに記載の図表を利用して実施して下さい。
PyMCの自己流モデルはテキストと異なる結果となってしまい、分析に利用するには慎重な判断を要する状況です。

PyMC実装
Let's enjoy PyMC & Python !
曲「H」の準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
import scipy.stats as stats
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込み
曲「H」のcsvファイルをpandasのデータフレームに読み込みます。
# データの読み込み
data = pd.read_csv('sample_data_h.txt')
display(data)【実行結果】
全7回の試行の記録です。
trial:試行番号
total_score:総合得点 ※目的変数
bonus:ボーナス点
censored:打ち切りフラグ
(打ち切りのないデータ、1:打ち切られたデータ)

3.データの外観・統計量
ひとまず要約統計量を確認します。
### 要約統計量の表示
data.describe().round(2)【実行結果】
平均得点は98.75点、すごく高得点です。

時系列(試行番号順)にプロットしましょう。
seabornのscatterplotを利用します。
テキストの図9.1を代替します。
### 曲Hの総合得点の推移 ★図9.1に対応
plt.figure(figsize=(5, 3))
sns.scatterplot(data=data, x='trial', y='total_score', size='bonus',
sizes=(20, 200))
plt.legend(title='bonus', bbox_to_anchor=(1, 1));【実行結果】
総合得点が高くなるにつれてボーナス得点が低くなる感じがします。


モデル1「打ち切られていないデータで推論」
テキストの「9.1.1 対策1:打ち切られた「真の総合得点」を推定する」のモデルです。
「切断正規分布」(TruncatedNormal)を活用します。
テキストの図9.2のイメージを確認しましょう。
### 想定する分布の描画 ★図9.2に対応
# 初期値設定 x軸の値、正規分布インスタンス
x = np.linspace(0, 150, 151)
dist = stats.norm(95, 10)
# 描画
plt.figure(figsize=(6, 3))
# 正規分布の確率密度関数の描画
plt.plot(x[45:145], dist.pdf(x[45:145]))
# x<=100の領域の塗りつぶし
plt.fill_between(x[100:145], 0, dist.pdf(x[100:145]), alpha=0.5)
# 修飾
plt.xlim(40, 150)
plt.title(r'想定する分布($\mu$=95, $\sigma$=10)')
plt.xlabel('total score')
plt.ylabel('density')
plt.show()【実行結果】
打ち切られた真の総合得点は100点を超える「青塗りの領域」で生成されるものと考察されています。
「青塗りの領域」の面積が1になるように拡大した分布が「切断正規分布」なのです。

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
目的変数$${y_{data}}$$の添字$${data}$$はデータのインデックスであり、$${data = 0, \cdots, 5}$$です。
$$
\begin{align*}
\mu &\sim \text{Uniform}\ (\text{lower}=-1000,\ \text{upper}=1000) \\
\sigma &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=1000) \\
y_{data} &\sim \text{Normal}\ (\text{mu}=\mu,\ \text{sigma}=\sigma) \\
y_{cens} &\sim \text{TruncatedNormal}\ (\text{mu}=\mu,\ \text{sigma}=\sigma,\ \text{lower}=100) \\
\end{align*}
$$
1.モデルの定義
打ち切りのない6回の試行データをdata_noncensordに格納します。
その後、coord、data、パラメータの事前分布、尤度、計算値をそれぞれ定義・指定します。
### モデルの定義
# 打ち切られていないデータを抽出(6個)
data_noncensored = data[data['censored']==0].reset_index(drop=True)
# モデルの定義
with pm.Model() as model1:
### データ関連定義
# coordの定義
model1.add_coord('data', values=data_noncensored.index, mutable=True)
# dataの定義
score = pm.ConstantData('score',
value=data_noncensored['total_score'].values,
dims='data')
### 事前分布
mu = pm.Uniform('mu', lower=-1000, upper=1000)
sigma = pm.Uniform('sigma', lower=0, upper=1000)
### 尤度
# 6試行の打ち切られていない部分のデータY
y = pm.Normal('y', mu=mu, sigma=sigma, observed=score, dims='data')
### 計算値:下限100の切断正規分布
# 下限100の切断正規分布(Truncated)
yCens = pm.TruncatedNormal('yCens', mu=mu, sigma=sigma, lower=100)【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次を設定しました行の座標:名前「data」、値「行インデックス」
dataの定義
目的変数$${score}$$:総合得点(打ち切りのないデータに限定)を設定しました。パラメータの事前分布
モデルの数式表現のとおりに設定しました。
テキスト・Stanスクリプトに無いパラメータ値は適当に設定しました。
尤度
打ち切りのないデータの総合得点$${y}$$が従う正規分布Normalです。
次元は「data」です。
計算値
下限100の切断正規分布に従う、打ち切られた真の総合得点$${y_{cens}}$$です。
2.モデルの外観の確認
### モデルの表示
model1【実行結果】
シンプルなモデルです。

# モデルの可視化
pm.model_to_graphviz(model1)【実行結果】

3.事後分布からのサンプリング
乱数生成数(draws, tune)はテキストと同様です。
ただし、thinは行っていません。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ20秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 22秒
with model1:
idata1 = pm.sample(draws=50000, tune=50000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.01}$$としています(この章の閾値は他の章よりも厳しい内容です)。
### r_hat>1.01の確認
rhat_idata1 = az.rhat(idata1)
(rhat_idata1 > 1.01).sum()【実行結果】
$${\hat{R}>1.01}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq1.01}$$であることを確認できました。

パラメータ等の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
var_names = ['mu', 'sigma', 'yCens']
pm.summary(idata1, hdi_prob=0.95, var_names=var_names)【実行結果】
テキストの表9.2の要約統計量と比べて、全てのパラメータ等の値が小さい、という結果になりました(汗)

トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata1,combined=True, var_names=var_names, figsize=(12, 7))
plt.tight_layout();【実行結果】
収束している感じがいたします。

5.分析~テキストにならって
テキスト表9.2の要約統計量の代替コードです。
### パラメータの事後分布の要約統計量 ★表9.2に対応
# μ, sigma, y_censの事後分布データの取得
mu_data = idata1.posterior.mu.stack(sample=('chain', 'draw')).data
sigma_data = idata1.posterior.sigma.stack(sample=('chain', 'draw')).data
y_cens_data = idata1.posterior.yCens.stack(sample=('chain', 'draw')).data
# 要約統計情報を計算する関数の定義
def calc_stat(x):
return [np.mean(x), np.median(x), np.std(x), np.quantile(x, 0.025),
np.quantile(x, 0.975)]
# 要約統計量のデータフレームの表示
df1 = pd.DataFrame({'μ': calc_stat(mu_data),
'σ': calc_stat(sigma_data),
'y_cens': calc_stat(y_cens_data)},
index=['平均値', '中央値', '標準偏差', '2.5%', '97.5%']).T
display(df1.round(3))【実行結果】
観測データの総合得点の平均値は$${98.54}$$であり、$${\mu}$$の平均値と同じです。
打ち切りのない真の総合得点$${y_{cens}}$$は、100点を達成した際に獲得した点です。テキストの$${101.16}$$と比べて$${0.37}$$小さい$${100.79}$$になりました。
テキストの推論と異なるのは、PyMC自己流モデルの設定が悪いのでしょうか・・・???

$${y}$$の事後予測データを取得してプロットしてみます。
### 事後予測のサンプリングの実施
with model1:
idata1.extend(pm.sample_posterior_predictive(idata1))【実行結果】

### ppcプロットの描画~散布図
pm.plot_ppc(idata1, kind='scatter')
plt.xlim(90, 108)
plt.legend(bbox_to_anchor=(1.5, 1));【実行結果】
オレンジの点線が$${y}$$の事後予測の平均値です。
きれいなベル型を描いています。
青い点が事後予測のサンプリングデータ点です。
100点よりも左側(下側)に多く分布しているようです。

6.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idata1をpickleで保存します。
### idataの保存 pickle
file = r'idata1_ch09.pkl'
with open(file, 'wb') as f:
pickle.dump(idata1, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata1_ch09.pkl'
with open(file, 'rb') as f:
idata1_load = pickle.load(f)
モデル2「打ち切りデータを活用して推論」
テキストの「9.1.2 対策2:打ち切りデータが発生する確率を利用する」のモデルです。
「切断正規分布」(TruncatedNormal)を活用します。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
目的変数$${y}}$$の添字$${noncensdata,\ censdata}$$は、打ち切りのないデータおよび打ち切りデータのインデックスです。
$${noncensdata=0, \cdots, 5}$$、$${censdata=6}$$です。
$$
\begin{align*}
\mu &\sim \text{Uniform}\ (\text{lower}=-1000,\ \text{upper}=1000) \\
\sigma &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=1000) \\
y_{noncensdata} &\sim \text{Normal}\ (\text{mu}=\mu,\ \text{sigma}=\sigma) \\
y_{censdata} &\sim \text{TruncatedNormal}\ (\text{mu}=\mu,\ \text{sigma}=\sigma,\ \text{lower}=100) \\
\end{align*}
$$
1.モデルの定義
打ち切りのない6回の試行データをdata_noncensordに格納します。
打ち切りのある1回の試行データをdata_censordに格納します。
その後、coord、data、パラメータの事前分布、尤度、計算値をそれぞれ定義・指定します。
### モデルの定義
# 打ち切られていないデータ・打ち切りデータを抽出
data_noncensored = data[data['censored']==0].reset_index(drop=True)
data_censored = data[data['censored']==1].reset_index(drop=True)
with pm.Model() as model2:
### データ関連定義
# coordの定義
model2.add_coord('dataNonCens', values=data_noncensored.index, mutable=True)
model2.add_coord('dataCens', values=data_censored.index, mutable=True)
# dataの定義
scoreNonCens = pm.ConstantData('scoreNonCens',
value=data_noncensored['total_score'].values,
dims='dataNonCens')
scoreCens = pm.ConstantData('scoreCens',
value=data_censored['total_score'].values,
dims='dataCens')
### 事前分布
mu = pm.Uniform('mu', lower=-1000, upper=1000)
sigma = pm.Uniform('sigma', lower=0, upper=1000)
### 尤度
# 6試行の打ち切られていない部分のデータY
y = pm.Normal('y', mu=mu, sigma=sigma,
observed=scoreNonCens, dims='dataNonCens')
# 1試行の打ち切られた部分のデータYcens
yCens = pm.TruncatedNormal('yCens', mu=mu, sigma=sigma, lower=100,
observed=scoreCens, dims='dataCens')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次を設定しました打ち切りのないデータの行の座標:名前「dataNonCens」、値「行インデックス」
打ち切りデータの行の座標:名前「dataCens」、値「行インデックス」
dataの定義
目的変数$${scoreNonCens}$$:打ち切りのないデータの総合得点、目的変数$${scoreCens}$$:打ち切りデータの総合得点を設定しました。パラメータの事前分布
モデルの数式表現のとおりに設定しました。
テキスト・Stanスクリプトに無いパラメータ値は適当に設定しました。
尤度
打ち切りのないデータの総合得点$${y}$$が従う正規分布Normalです。
次元は「data」です。打ち切りデータの総合得点$${y_{cens}}$$が従う下限100の切断正規分布TruncatedNormalです。
次元は「data」です。
テキストでは打ち切りデータの総合得点は標準正規分布の上側確率としていますが、ここでのPyMCモデルは切断正規分布を用います。
切断正規分布の適否に自信は無いです(泣)
2.モデルの外観の確認
### モデルの表示
model2【実行結果】
モデル1との違いが表現されていません・・・。

# モデルの可視化
pm.model_to_graphviz(model2)【実行結果】
「打ち切りのないデータの総合得点が従う正規分布」と「打ち切りデータの総合得点が従う切断正規分布」の両方で、共通の平均パラメータ mu と標準偏差パラメータ sigma を使っていることが分かります!

3.事後分布からのサンプリング
乱数生成数(draws, tune)はテキストと同様です。
ただし、thinは行っていません。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ10秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 10秒
with model2:
idata2 = pm.sample(draws=50000, tune=50000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.01}$$としています(この章の閾値は他の章よりも厳しい内容です)。
### r_hat>1.01の確認
rhat_idata2 = az.rhat(idata2)
(rhat_idata2 > 1.01).sum()【実行結果】
$${\hat{R}>1.01}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq1.01}$$であることを確認できました。

パラメータ等の事後分布の要約統計量です。
#### 推論データの要約統計情報の表示
pm.summary(idata2, hdi_prob=0.95)【実行結果】
テキストの表9.2の要約統計量と比べて、全てのパラメータ等の値が小さい、という結果になりました(汗)
また、打ち切りデータの総合得点100点を含めたにも関わらず、$${\mu}$$の平均値はモデル1よりも小さな値になりました(泣)

トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata2,combined=True, figsize=(12, 5))
plt.tight_layout();【実行結果】
収束している感じがいたします。

5.分析~テキストにならって
テキスト表9.3の要約統計量の代替コードです。
### パラメータの事後分布の要約統計量 ★表9.3に対応
# μ, sigma, y_censの事後分布データの取得
mu_data2 = idata2.posterior.mu.stack(sample=('chain', 'draw')).data
sigma_data2 = idata2.posterior.sigma.stack(sample=('chain', 'draw')).data
# 要約統計情報を計算する関数の定義
def calc_stat(x):
return [np.mean(x), np.median(x), np.std(x), np.quantile(x, 0.025),
np.quantile(x, 0.975)]
# 要約統計量のデータフレームの表示
df2 = pd.DataFrame({'μ': calc_stat(mu_data2),
'σ': calc_stat(sigma_data2)},
index=['平均値', '中央値', '標準偏差', '2.5%', '97.5%']).T
display(df2.round(3))【実行結果】
$${\mu}$$の平均値はテキストの$${98.917}$$と比べて$${0.47}$$小さい結果になりました。
テキストの推論と異なるのは、PyMC自己流モデルの設定が悪いのでしょうか・・・???

$${y,\ y_{cens}}$$の事後予測サンプリングを行って、プロットしてみましょう。
### 事後予測のサンプリングの実施
with model2:
idata2.extend(pm.sample_posterior_predictive(idata2))【実行結果】

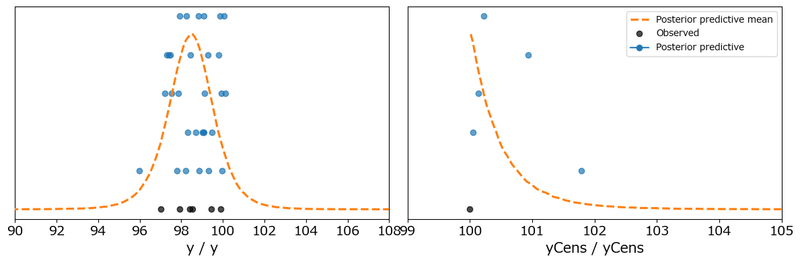
### ppcプロットの描画~散布図
fig, ax = plt.subplots(1, 2, figsize=(12, 4))
pm.plot_ppc(idata2, kind='scatter', legend=False, ax=ax)
ax[0].set_xlim(90, 108)
ax[1].set_xlim(99, 105)
ax[1].legend()
plt.tight_layout();【実行結果】
こちらも$${y}$$はきれいなベル型です。
モデル1と比べると100点を超えるサンプルデータが多い印象です。
打ち切りデータの$${y_{cens}}$$のサンプルデータは100~102点の間にあり、やや100点側に偏った放物線のような雰囲気です。
6.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idata2をpickleで保存します。
### idataの保存 pickle
file = r'idata2_ch09.pkl'
with open(file, 'wb') as f:
pickle.dump(idata2, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata2_ch09.pkl'
with open(file, 'rb') as f:
idata2_load = pickle.load(f)
曲「S」の準備・データ確認
1.データの読み込み
曲「S」のcsvファイルをpandasのデータフレームに読み込みます。
# データの読み込み
data2 = pd.read_csv('./data/sample_data_s.txt')
print(data2.shape)
display(data2.tail())【実行結果】
全30回の試行の記録のうち、最後の5試行を表示しています。
trial:試行番号
total_score:総合得点 ※目的変数
raw_score:素点
bonus:ボーナス点

3.データの外観・統計量
ひとまず要約統計量を確認します。
### 要約統計量の表示
data2.describe().round(2)【実行結果】
平均得点は97.91点、こちらも、すごく高得点です。

時系列(試行番号順)にプロットしましょう。
seabornのscatterplotを利用します。
テキストの図9.3を代替します。
### 曲Sの総合得点の推移 ★図9.3に対応
plt.figure(figsize=(7, 3))
sns.scatterplot(data=data2, x='trial', y='total_score', size='bonus',
sizes=(20, 200))
plt.legend(title='bonus', bbox_to_anchor=(1, 1));【実行結果】
試行を進めるにつれて、得点が上下に揺らぐ雰囲気を感じます。


状態空間モデル
テキストの「9.2 これからも100点を取れるのか」のモデルです。
pymc_experimentalを用いて状態空間モデルを構築します。
pymc_experimentalのインストール(必要に応じて)
pymc_experimentalの公式サイトに掲載のインストール方法は、Gitリポジトリからインストールする方法です。
そこで、まずGitアプリをインストールして、次にpymc_experimentalをインストールします。
■ Gitアプリのインストール
私はこちらのサイトからGitアプリをダウンロードしました。
Windows版のインストールの手順は、こちらのサイトの情報を参考にしました。
■pymc_experimentalのインストール
pymc_experimental公式サイトのインストールコードをそのまま実行しました。
pip install git+https://github.com/pymc-devs/pymc-experimental.gitインストールしたpymc_experimentalのバージョンは 0.0.12 です。
### バージョン確認
import pymc_experimental
pymc_experimental.__version__【実行結果】

pymc_experimentalの状態空間モデルからstructuralをインポートします。
### インポート
from pymc_experimental.statespace import structural as stモデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
状態空間モデルっぽく書きます。
■状態方程式(システムモデル)
$${\mu_t = \mu_{t-1} + \xi_{t}, \quad \xi_t \sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\xi})}$$
■観測方程式(観測モデル)
$${y_t = \mu_t + \epsilon_t, \quad \epsilon_t \sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\epsilon})}$$
■事前分布
$${\sigma_{\xi} \sim \text{HalfStudentT}\ (\text{nu}=3,\ \text{sigma}=100)}$$
$${\sigma_{\epsilon} \sim \text{HalfStudentT}\ (\text{nu}=3,\ \text{sigma}=100) }$$
$${\mu_0 \sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=100) }$$
状態空間モデルのイメージ図を再掲します。

このモデルの状態方程式は、レベル成分と正規分布に従うシステムノイズ$${\xi_t}$$で構成されます。
実装では「LevelTrendComponent」(レベル・トレンド成分)にかかわります。
観測方程式は真の値$${\mu_t}$$に正規分布に従う観測ノイズ$${\epsilon_t}$$で構成されます。
実装では観測ノイズが「MeasurementError」(観測誤差)にかかわります。
1.モデルの定義
状態空間モデルの定義とPyMCモデルの定義に分けて書きます。
まずは状態空間モデルの定義から。
### 状態空間モデルの定義
# レベル・トレンドコンポーネントの定義
# μt = μt-1 + ξt, ξt ~ Normal(0, σξ)
trend = st.LevelTrendComponent(order=1, innovations_order=1)
# 測定ノイズの定義 分散パラメータσε
error = st.MeasurementError()
# レベル・トレンドと観測ノイズで状態空間モデルを構築
ss_mod = (trend + error).build()【モデル注釈】
trend = st.LevelTrendComponent(order=1, innovations_order=1)
状態方程式$${\mu_t = \mu_{t-1} + \xi_{t}}$$を定義しています。
orderで時間依存する状態変数の個数を指定、innovations_orderでシステムノイズの個数を指定する模様です。
今回のモデルでは、時間依存する状態変数は$${\mu_t}$$の1個、システムノイズは$${\xi_t}$$の1個です。以下の公式サイトの例示が分かりやすいかと思います。
(ガウスランダムウォークであることを覚えておいて下さい)

error = st.MeasurementError()
観測ノイズ$${\epsilon_t}$$を設定しています。
ss_mod = (trend + error).build()
観測方程式$${y_t = \mu_t + \epsilon_t}$$を定義して、.build()で状態空間モデルを構築します。
レベル・トレンド・成分と観測ノイズの足し算で簡単に定義できる模様です。
【実行結果】
PyMCモデルで「事前分布」の設定が必要なパラメータが表示されます。
変数名、dim名、形状(shape)は指定通りに設定する必要があるとのこと。

initial_trend:$${\mu_0}$$の事前分布だろうと想定しました。
sigma_trend:システムノイズが従う正規分布の標準偏差$${\sigma_{\xi}}$$の事前分布だろうと想定しました。
sigma_MeasurementError:観測ノイズが従う正規分布の標準偏差$${\sigma_{\epsilon}}$$の事前分布だろうと想定しました。
P0:何者でしょう?制約は「半正定値」(Positive semi-definite)の形状$${(1,1)}$$ということで、参考サイトの$${\text{Gamma}}$$分布を用いて対角行列を生成する定義を借用することにします。
続いて、PyMCのモデル定義です。
### PyMCモデルの定義
with pm.Model(coords=ss_mod.coords) as model_ss:
# パラメータの事前分布
intitial_trend = pm.Normal('initial_trend', mu=0, sigma=100,
dims=['trend_state'])
sigma_trend = pm.HalfStudentT('sigma_trend', nu=3, sigma=100,
dims=['trend_shock'])
sigma_MeasurementError = pm.HalfStudentT('sigma_MeasurementError', nu=3,
sigma=100)
P0_diag = pm.Gamma('P0_diag', alpha=1, beta=1, dims=['state'])
P0 = pm.Deterministic('P0', pt.diag(P0_diag), dims=['state', 'state_aux'])
# 状態空間モデルの計算グラフ構築
ss_mod.build_statespace_graph(data=data2['total_score'], mode='JAX')【実行結果】なし
パラメータの事前分布には、さきほど状態空間モデルから指示をいただいたものについて定義しました。
最後に、状態空間モデル ss_mod に対して、build_statespace_graphを実行して、状態空間モデルと観測データを結びつけてモデルを構築します。
引数 data に目的変数(観測値) を設定しています。
2.モデルの外観の確認
変数内に"_" (アンダースコア)を含んでいるせいか、「model」を実行するとKaTexエラーになってしまいます。
そこで、__getstate__()メソッドで状態空間モデルの内部を覗いてみましょう。
### モデルの表示()
model_ss.__getstate__()【実行結果】
載せきれません・・・。
モデル内部では、ものすごいことが起きている予感がします。

モデルを可視化しましょう。
### モデルの可視化
pm.model_to_graphviz(model_ss)【実行結果】
・・・(言葉を失いました)
電子回路のような複雑怪奇さに驚きました。

左下に注目すると、3つの状態変数が見つかります。

3.事後分布からのサンプリング
乱数生成数(draws, tune)はテキストと同様です。
ただし、thinは行っていません。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ65秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 65秒
with model_ss:
idata_ss = pm.sample(draws=50000, tune=50000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.01}$$としています(この章の閾値は他の章よりも厳しい内容です)。
### r_hat>1.01の確認
rhat_idata_ss = az.rhat(idata_ss)
(rhat_idata_ss > 1.01).sum()【実行結果】
$${\hat{R}>1.01}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq1.01}$$であることを確認できました。
パラメータ等の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
pm.summary(idata_ss, hdi_prob=0.95)【実行結果】
パラメータ数が多いので見切れています。
また、テキストに要約統計量の記載がないので、一致しているかどうかを確かめられません。

トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata_ss, combined=True, figsize=(12, 20))
plt.tight_layout();【実行結果】
バーコードは収束していない(発散している)データを示しています。
かなり収束していないデータが混在しているようです。
$${\hat{R}}$$の確認で収束したことにしています。

5.分析~テキストにならって
状態変数の事後分布からのサンプリングを実行します。
状態空間モデル ss_mod に対して、sample_conditional_posterior()メソッドを適用します。
# 状態変数の事後分布からのサンプリングの実行 2分30秒
post = ss_mod.sample_conditional_posterior(idata_ss, random_seed=1234)【実行結果】
5つの変数がサンプリングの対象です。

総合得点の事後分布を可視化しましょう。
### 事後分布データの加工
# データの整理(chainとdrawの次元を統合)
post_stacked = post.stack(sample=('chain', 'draw'))
# 95%HDI区間、50%HDI区間の算出
hdi95_post = az.hdi(post, hdi_prob=0.95
).smoothed_posterior_observed.squeeze().values
hdi95_lower_post = hdi95_post[:, 0]
hdi95_upper_post = hdi95_post[:, 1]
hdi50_post = az.hdi(post, hdi_prob=0.50
).smoothed_posterior_observed.squeeze().values
hdi50_lower_post = hdi50_post[:, 0]
hdi50_upper_post = hdi50_post[:, 1]
### 事後分布の描画
plt.figure(figsize=(10, 4))
# 観測値の描画
plt.scatter(data2['trial'], data2['total_score'], color='black', label='観測値')
# 事後分布の描画
plt.plot(data2['trial'],
post_stacked.smoothed_posterior_observed.squeeze().mean(axis=1).data,
color='steelblue', label='事後分布の平均値')
plt.fill_between(data2['trial'], y1=hdi95_lower_post, y2=hdi95_upper_post,
color='steelblue', alpha=0.1, label='事後分布95%HDI')
plt.fill_between(data2['trial'], y1=hdi50_lower_post, y2=hdi50_upper_post,
color='steelblue', alpha=0.3, label='事後分布50%HDI')
# 修飾
plt.legend(loc='lower right')
plt.show()【実行結果】
テキストの区間は信用区間ですが、このコードではHDI区間を表示しています。
テキストの図9.4のグラフと比べると、50%区間も95%区間も、区間が広くなってしまいました。

将来予測のサンプリング取得を実行しましょう。
テキストに合わせて、31回めの試行(つまり1期先)を予測します。状態空間モデル ss_mod に対して、forecast()メソッドを適用します。
簡単に将来予測ができるので、使い勝手がいいです!
### 将来予測のサンプリングの実行 60秒
# 初期値設定:予測期間
n_periods = 2
# 将来予測のサンプリングの実行
forecasts = ss_mod.forecast(idata_ss, start=data2.index[-1], periods=n_periods)【実行結果】

30試行までの事後分布と31試行の予測をまとめて可視化しましょう。
テキストの図9.4に代替します。
### 事後分布と将来予測のHDI区間の描画
plt.figure(figsize=(10, 5))
## 100点の水平線の描画
plt.axhline(100, color='gray', lw=0.8, ls='--')
## 観測値の描画
plt.scatter(data2['trial'], data2['total_score'], color='black', s=15,
label='観測値')
## 学習期間の描画
# 95%HDIの描画
plt.fill_between(data2['trial'], y1=hdi95_lower_post, y2=hdi95_upper_post,
color='steelblue', alpha=0.2, label='事後分布95%HDI')
# 50%HDIの描画
plt.fill_between(data2['trial'], y1=hdi50_lower_post, y2=hdi50_upper_post,
color='steelblue', alpha=0.5, label='事後分布50%HDI')
# 事後分布の平均値の描画
plt.plot(data2['trial'],
post_stacked.smoothed_posterior_observed.squeeze().mean(axis=1).data,
color='steelblue', label='事後分布の平均')
## 将来期間の描画
# 95%HDIの描画
plt.fill_between(forecasts.coords['time'] + 1,
y1=hdi95_lower_forecasts, y2=hdi95_upper_forecasts,
color='tomato', alpha=0.2, label='将来予測95%HDI')
# 50%HDIの描画
plt.fill_between(forecasts.coords['time'] + 1,
y1=hdi50_lower_forecasts, y2=hdi50_upper_forecasts,
color='tomato', alpha=0.5, label='将来予測50%HDI')
# 将来予測の平均値の描画
plt.plot(forecasts.coords['time'] + 1,
forecasts_stacked.forecast_observed.squeeze().mean(axis=1).data,
color='tomato', alpha=1, label='将来予測の平均')
## 修飾
text = f'31試行目の95%予測区間 [{hdi95_lower_forecasts[1]:.3f}, ' \
f'{hdi95_upper_forecasts[1]:.3f}]'
plt.title(f'歌唱力の事後分布と将来予測のHDI区間\n{text}')
plt.xlabel('試行回数')
plt.ylabel('得点')
plt.legend()
plt.show()【実行結果】
テキストの区間は信用区間ですが、このコードではHDI区間を表示しています。
赤い部分が31回目の試行の予測です。
事後分布・将来予測のHDI区間はテキストよりも広くなっています。
ただし、31試行目の95%予測区間は、テキストの$${[96.890,\ 101.775]}$$に近い値となりました。
なお、折れ線で示しているのは平均値です。
テキストの破線は中央値ですので、違いがあることにご留意ください。

※補足
plot_hdi関数を用いて事後分布と将来予測の区間を描画すると、区間のつなぎ目がズレるんです。
理由は分かりませんが、plot_hdi関数はおそらく平滑化しているのではないかと想像しています。
arvizのhdi関数で区間の下限・上限値を計算してプロットするコードは、つなぎ目がピッタリ繋がっています。
ぱぐみさんが書いたコードは凄いです!
6.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idata2_ssをpickleで保存します。
### idataの保存 pickle
file = r'idata_ss_ch09.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_ss, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_ss_ch09.pkl'
with open(file, 'rb') as f:
idata_ss_load = pickle.load(f)
おまけモデル
PyMCのガウスランダムウォークモデルを試してみます。
今回の状態空間モデルは、状態方程式が「ランダムウォーク」です。
$$
\begin{align*}
\sigma_{\xi} &\sim \text{HalfStudentT}\ (\text{nu}=3,\ \text{sigma}=100) \\
\sigma_{\epsilon} &\sim \text{HalfStudentT}\ (\text{nu}=3,\ \text{sigma}=100) \\
\mu_0 &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=100) \\
\mu_t &\sim \text{GaussianRandomWalk}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\xi},\ \text{init}=\mu_o) \\
y_t &\sim \text{Normal}\ (\text{mu}=\mu,\ \text{sigma}=\sigma_{\epsilon})
\end{align*}
$$
【ランダムウォーク】
次数1の自己回帰モデル$${\text{AR(1)}}$$(次式参照)について、自己回帰係数$${\phi_1=1}$$のとき、ランダムウォークと呼ばれます。
$${y_t = \phi_1 y_{t-1} + \varepsilon_t, \quad \varepsilon_t \sim \text{Normal}(0, \sigma^2)}$$
今回の状態方程式(次式参照)は、次数1、自己回帰係数$${\phi_1=1}$$の自己回帰モデルです。
$${\mu_t = 1 \times \mu_{t-1} + \xi_{t}, \quad \xi_t \sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=\sigma_{\xi})}$$
ローカル・レベル・モデルは、ランダムウォークに観測誤差が加わったモデルであり、「ランダムウォーク・プラス・ノイズモデル」とも呼ばれるそうです。
PyMCのモデルの定義です。
# モデルの定義
with pm.Model() as model_rw:
### データ関連定義
# coordの定義
model_rw.add_coord('data', values=data2['trial'].values, mutable=True)
score = pm.ConstantData('score', value=data2['total_score'].values,
dims='data')
### 事前分布
sigmaXi = pm.HalfStudentT('sigmaXi', nu=3, sigma=100)
sigmaEpsilon = pm.HalfStudentT('sigmaEpsilon', nu=3, sigma=100)
initDist = pm.Normal.dist(mu=0, sigma=100)
mu = pm.GaussianRandomWalk('mu', mu=0, sigma=sigmaXi, init_dist=initDist,
dims='data')
### 尤度
y = pm.Normal('y', mu=mu, sigma=sigmaEpsilon, observed=score, dims='data')モデルを表示します。
### モデルの表示
model_rw【実行結果】

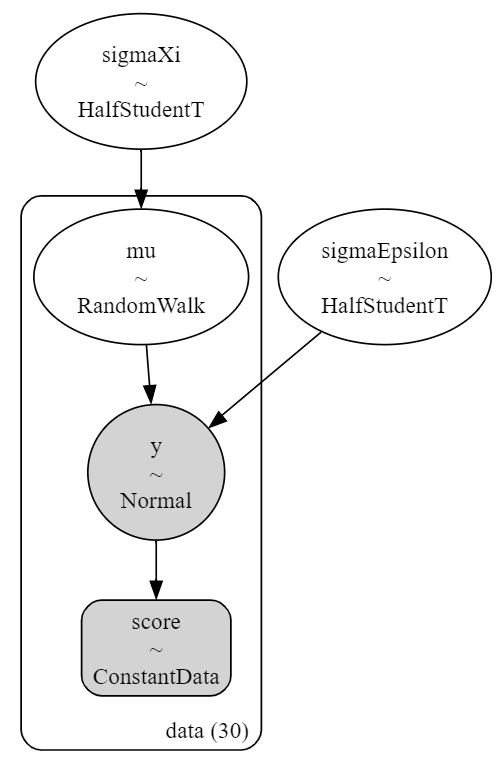
モデルを可視化します。
# モデルの可視化
pm.model_to_graphviz(model_rw)【実行結果】
状態空間モデルと比べるととてもシンプルなモデルです。
事後分布からのサンプリングを実行します。
およそ40秒かかりました。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 40秒
with model_rw:
idata_rw = pm.sample(draws=50000, tune=50000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)$${\hat{R}}$$はすべて$${1.01}$$以下でした。
### r_hat>1.01の確認
rhat_idata_rw = az.rhat(idata_rw)
(rhat_idata_rw > 1.01).sum()【実行結果】

トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata_rw, combined=True, figsize=(12, 7))
plt.tight_layout();【実行結果】
drawの最初の方に発散のバーコードが見られます。
$${\hat{R}}$$より、収束していることにしています。

事後予測からのサンプリングを実行しましょう。
### 事後予測の乱数データの取得
with model_rw:
pred_rw = pm.sample_posterior_predictive(idata_rw, random_seed=1234)【実行結果】

では、お待ちかねの事後分布のプロットです。
### 事後予測のプロット
# 事後予測の平均値の算出
pred_y_mean_rw = pred_rw.posterior_predictive.y.mean(dim=('chain', 'draw')).data
# 描画
fig, ax = plt.subplots(figsize=(10, 5))
# 観測データのtotal_scoreの散布図の描画
ax.scatter(data2['trial'], data2['total_score'], color='black', label='観測値')
# 事後予測値の平均値の折れ線グラフの描画
ax.plot(data2['trial'], pred_y_mean_rw, color='steelblue', label='事後平均')
# 事後予測値のHDI:95%の描画
pm.plot_hdi(data2['trial'], pred_rw.posterior_predictive.y, hdi_prob=0.95,
fill_kwargs={'color': 'steelblue', 'alpha': 0.2, 'label': '95%HDI'})
# 事後予測値のHDI:50%の描画
pm.plot_hdi(data2['trial'], pred_rw.posterior_predictive.y, hdi_prob=0.50,
fill_kwargs={'color': 'steelblue', 'alpha': 0.5, 'label': '50%HDI'})
# 修飾
plt.xlabel('試行回数')
plt.ylabel('得点')
plt.title('歌唱力の信用区間')
plt.legend(loc='lower right')
plt.show()【実行結果】
plot_hdi関数を用いてHDI区間を描画しているので、輪郭が滑らかになっています。
状態空間モデルと比べて、区間が狭い感じがします。
なお、将来予測の方法がわからないので、予測区間の描画は省略いたします(泣)

以上で第9章は終了です。
おわりに
真の総合得点を自己採点
この章を実践する途中でふと気がついたこと、それは、ベイズ推論の対象はいつもは確率分布のパラメータですが、今回は目的変数が推論の対象になっていたことです。
なので、事後予測が活躍したのですね。
そして、もう1つ気がついたことがあります。
PyMCで割りと気軽に状態空間モデルを書けるということです。
はやく「experimental」状態から「formal」状態、つまり、PyMC本体に状態空間モデルが追加されて欲しい、と思いました。
時系列モデルの将来予測を少ないコード量で書けることで、Pythonによる時系列分析にPyMCのベイズ推論という選択肢が増えます。
強力な分析手段になることでしょう。
PyMC本体の状態空間モデル化、すごく楽しみです。
今回のモデルでは、テキストの統計量よりも下方にズレてしまい、申し訳なく思う反面、状態空間モデルを動かせたという経験を獲得でき、私の心身に好ましい状態を観測できました。
ですので、実質的な自己採点は・・・

シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ(お題)を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます!
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。
最後までお読みいただきまして、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
