5-4 ２項分布の正規近似～出口調査で二項分布と標本比率を深掘りして、母比率との差の確率を計算

ネイピア DS

2023年6月7日 11:43

今回の統計トピック

標本比率を確率変数にして正規分布近似を用いた確率計算を行います！
二項分布の深掘りも行います！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解く

📘公式問題集のカテゴリ

確率分布の分野
問4 ２項分布の正規近似（投票の出口調査）

試験実施年月
調査中（類似問題：統計検定2級 2019年11月問13（回答番号22）

問題

公式問題集をご参照ください。

解き方

題意
母比率の推定において、標本サイズ$${n}$$が大きい場合に標本比率$${\hat{p}}$$が近似的に正規分布に従う性質を利用して、標本比率$${\hat{p}}$$を確率変数としたときの確率を計算します。

標本サイズ$${n=100}$$、ある候補者への投票者数$${x=54}$$、ある候補者の真の得票率（母比率）$${p}$$のとき、ある候補者の標本得票率（母比率の推定値）$${\hat{p}=x/n}$$を確率変数とする確率$${P(|\hat{p}-p| \leq 0.1)}$$の近似値を求めます。

公式問題集の記載内容を改変

作戦会議
正規分布の確率計算のときは、確率$${P}$$のかっこ内の「確率変数を標準化」して、「標準正規分布の上側確率表」から確率を取得する解答シナリオを描きましょう！
この問題では「母比率の推定値」である「標本比率$${\hat{p}}$$」を標準化します。
標本比率の期待値と分散から、近似する正規分布のパラメータを定めて、正規分布の標準化の公式を当てはめます。

以下、少々機械的に書きます。

標本比率
投票者全体の中から$${n=100}$$人を標本抽出して、ある候補者への投票者数$${x=54}$$人を得ます。
標本比率$${\hat{p}=x/n=54/100=0.54}$$です。
$${p}$$の上の$${\ \hat{}}$$（ハット）は推定値であることを表しています。

■公式
・標本比率$${\hat{p}=x/n}$$

標本比率の期待値と分散
標本比率$${\hat{p}}$$の期待値$${E[\hat{p}]}$$と分散$${V[\hat{p}]}$$は次のとおりです。
$${p}$$は母集団の母比率、$${n}$$は標本サイズ$${100}$$です。

■公式
・標本比率の期待値$${E[\hat{p}]=p}$$
・標本比率の分散$${V[\hat{p}]=\cfrac{p(1-p)}{n}}$$

正規分布近似
標本サイズ$${n}$$が大きいとき、中心極限定理により、標本比率は正規分布に近似的に従います。
このとき、正規分布のパラメータである平均と分散は次のようになります。

■公式
・平均＝標本比率の期待値$${E[\hat{p}]=p}$$
・分散＝標本比率の分散$${V[\hat{p}]=\cfrac{p(1-p)}{n}}$$

標準誤差
標本サイズ$${n}$$が大きい場合、標本比率$${\hat{p}}$$が母比率$${p}$$に近づくという大数の法則を利用して、標本比率の分散の式に含まれる$${p}$$を$${\hat{p}}$$に置き換えて、標準誤差を求めます。

■公式
・標準誤差$${=\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}}$$

■標本平均の分散・標準偏差、標準誤差
・標本平均の分散：$${p(1-p)/n}$$
・標本平均の標準偏差：$${\sqrt{p(1-p)/n}}$$
・標準誤差：$${\sqrt{\hat{p}(1-\hat{p})/n}}$$

標準化
標準化の式$${Z=\frac{X-\mu}{\sigma}}$$に対して、確率変数$${X}$$に標本比率$${\hat{p}}$$、平均$${\mu}$$に母比率$${p}$$、標準偏差$${\sigma}$$に標準誤差$${\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}}$$を当てはめます。
得られた$${z}$$は近似的に標準正規分布$${N(0,1)}$$に従います。

■公式
・標本比率の標準化$${z=\cfrac{\hat{p}-p}{\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}}}$$

問題に戻ります。

標準化の実施と解答
確率のかっこ内の確率変数を$${\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}}$$で割って標準化します。

$$
\begin{align*}
P(|\hat{p}-p| \leq 0.1)&=P \left( \left| \cfrac{\hat{p}-p}{\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}} \right| \leq \cfrac{0.1}{\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}} \right)\\
\\
&=P \left( |z| \leq \cfrac{0.1}{\sqrt{\cfrac{0.54\times0.46}{100}}} \right)\\
\\
&\approx P(|z| \leq 2.01)\\
&=P(-z \leq 2.01, z \leq 2.01)\\
&=P(z \geq -2.01, z \leq 2.01)\\
&=P(-2.01 \leq z \leq 2.01)\\
&=1-2 \times P(z > 2.01)　※補足①参照\\
&=1- 2 \times 0.0222　※補足②参照\\
&=1-0.0444\\
&=0.9556\\
\end{align*}
$$

答えは 0.96 です。
お疲れ様でした。

補足①　正規分布の両側確率
確率$${P(z<-2.01)}$$と確率$${P(z>2.01)}$$は同値です。
次の図の白い領域をご覧ください。
正規分布は平均$${\mu}$$を境にして左右対称なのです。

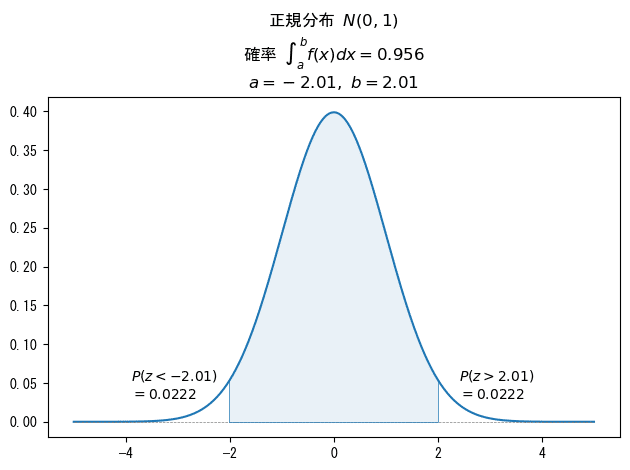
補足②　標準正規分布の上側確率
$${z}$$値$${=2.01}$$の上側確率$${P(z>2.01)}$$は、標準正規分布の上側確率表より$${0.0222}$$です。
次の図の赤い枠の部分です。

解答

⑤ 0.96 です。

難易度　ややむずかしい

・知識：標本比率、標本比率の期待値と分散、正規分布近似、標準正規分布
・計算力：数式組み立て（中）、数式計算（中）
・時間目安：2分

知る

おしながき

公式問題集の問題に接近してみましょう！
今回は、母比率の推定の目線で標本比率の正規分布近似のテーマに取り組みます！
母比率の推定～二項分布～二項分布の期待値・分散～標本比率の期待値・分散～正規分布近似～確率計算を巡って類似問題を旅します。

母比率の推定

📕公式テキスト：3.3.4 母比率の推定（118ページ～）

母比率と標本比率

たとえば選挙の出口調査のように、投票者の全体から一部の投票者を抽出して、ある候補者の得票率を推定して当落を予想する場面を想像しましょう。
投票者の全体が「母集団」であり、母集団から無作為抽出などの方法によって取り出した一部の投票者の投票データを「標本」と呼びます。
ある候補者の得票率は、投票者全体のうち、ある候補者に投票する「割合」です。
この「ある候補者の得票率」について、投票者全体＝母集団における割合（得票率）を「母比率」と呼びます。
一部の投票者から得た割合（得票率）を「標本比率」と呼びます。

母比率の推定
母比率の推定は多くの場合、「ある候補者の得票率はおよそ◯％から◯％と推定される」のように、一定の区間を推定する「区間推定」の場面で用いられます。
区間推定のテーマを取り扱う「統計的推定」の深掘りは今回はパスします。

標本比率と二項分布の関係
標本比率の正規分布近似は二項分布をベースにした議論なのです。
ということで、二項分布に飛びます！

二項分布

📕公式テキスト：2.7.2 二項分布（72ページ～）

たとえば、表を当たり、裏をはずれとするコイントスをします。
コイントスを10回行って表の出る回数が3回である確率を取り扱うのが二項分布なのです。

二項分布の定義へ向かいます。

正常なコインの場合、表の出る確率は$${1/2}$$です。
この確率を「成功確率$${p}$$」と呼びます。成功確率$${p}$$は$${1/2}$$で一定です。
なお、失敗確率は$${1-p=1/2}$$です。
トスを10回行うことを「試行を10回行う」と言い換えます。
表の出る回数3回を「成功回数が3回」と言い換えます。

実際のコイントスは偶然性が入るので、毎回試行結果が異なります。
一定の成功確率で毎回結果が異なる（互いに独立である）試行をベルヌーイ試行と呼びます。

二項分布とは
成功確率$${p}$$のベルヌーイ試行を$${n}$$回行うときの成功回数を表す確率変数$${X}$$の確率分布は、二項分布$${Bin(n,p)}$$に従います。

コイントスの例では、成功確率$${1/2}$$のベルヌーイ試行を$${10}$$回行うときの、成功回数$${3}$$回を表す確率変数$${X=3}$$の確率分布は、二項分布$${Bin(10, 1/2)}$$に従います、となります。

二項分布の確率
二項分布は離散型の確率分布です。
二項分布$${Bin(n,p)}$$に従う確率変数$${X=x}$$の確率質量関数$${f(x)}$$は次のようになります。

■公式：二項分布の確率質量関数
$${P(X=x) \equiv f(x) =\ _nC_x \ p^x \ (1-p)^{n-x} \qquad (x=0, 1, 2, \cdots, n) }$$

■公式：組み合わせの計算
$${_nC_x=\cfrac{n!}{(n-x)!x!}=\cfrac{n \times n-1\times \cdots \times n-x+1}{x \times x-1 \times \cdots \times 1}}$$

コイントスの例では、次のような計算で確率を求めることができます。

$$
\begin{align*}
f(x) &=\ _nC_x \ p^x \ (1-p)^{n-x}\\
\\
&=\ _{10}C_{3}\ \left( \frac{1}{2} \right) ^3\ \left(1-\frac{1}{2} \right)^{10-3}\\
\\
&=\cfrac{10!}{3!7!} \times \left( \frac{1}{2} \right) ^3 \times \left( \frac{1}{2} \right)^7\\
\\
&=\cfrac{10\times9\times8}{3\times2\times1}\times \cfrac{1}{2\times2\times2\times2\times2\times2\times2\times2\times2\times2}\\
&=\cfrac{\cancel{10}\ 5 \times \cancel9\ 3 \times \cancel8}{\cancel3\times\cancel2\times1}\times \cfrac{1}{\cancel 2\times\cancel2\times\cancel2\times2\times2\times2\times2\times2\times2\times2}\\
&=\cfrac{15}{128}\\
&=0.1171\cdots
\end{align*}
$$

コインを10回投げて表が3回出る確率は 11.7% です。
表が出る回数と確率の分布表は次のとおりです。

二項分布の可視化
コイントスの例をグラフにしました。
なんだか正規分布の形状に似ていますね。

試行回数$${n=1000}$$のグラフです。
試行回数$${n}$$が大きいとき、二項分布は正規分布に近似します。

二項分布の期待値と分散
二項分布$${Bin(n,p)}$$の期待値と分散は次のようになります。

■公式：二項分布の期待値
$${E[X]=np}$$

■公式：二項分布の分散
$${V[X]=np(1-p)}$$

コイントスの例の期待値と分散をみてみましょう。
・期待値$${E[X]=np=10\times1/2=5}$$回
・分散$${V[X]=np(1-p)=10\times1/2\times(1-1/2)=2.5}$$

表の出る確率が$${1/2}$$のコインを$${10}$$回トスするとき、表が出る回数の期待値が$${5}$$回というのは納得できますね！

二項分布の期待値と分散は、標本比率の期待値と分散の場面で再登場します。お楽しみに。

標本比率に戻ります。
以後は、「類題」を用いてお話を進めます。

類題

無作為抽出した100人に選挙の出口調査を行ったところ、X候補者に投票した人$${x}$$は 52人であり、得票率（標本比率）$${\hat{p}}$$は 0.52 でした。
母集団のX候補者の得票率（母比率）を$${p}$$とし、標本比率$${\hat{p}}$$を確率変数とするとき、確率$${P(|\hat{p}-p| \leq 0.05)}$$の近似値を求めましょう。
なお、二項分布は近似的に正規分布に従うものとします。

二項分布の期待値と分散
類題の数字を整理します。
・標本サイズ$${n=100}$$
・成功確率$${p=0.52}$$
100人の標本$${n=100}$$のうちX候補者に投票した人の数$${x}$$は二項分布$${Bin(100, 0.52)}$$に従うと想定します。
二項分布$${Bin(100, 0.52)}$$は、期待値$${E[x]=np=100\times0.52=52}$$、分散$${V[x]=np(1-p)=100\times0.52\times0.48=24.96}$$です。

グラフにしてみます。正規分布に似ています。

以下、しばらく機械的に書きます。

標本比率の期待値と分散
X候補者に投票した人の標本比率$${\hat{p}}$$は、標本サイズ$${n}$$と投票数$${x}$$を用いて、$${\hat{p}=x/n}$$と表します。
標本比率の期待値$${E[\hat{p}]}$$と分散$${V[\hat{p}]}$$は、二項分布の期待値・分散と、期待値・分散の演算公式から導出できます。

確率変数$${X}$$について
・二項分布の期待値$${E[X]=np}$$
・二項分布の分散の期待値$${V[X]=np(1-p)}$$
・期待値の演算$${E[aX]=aE[X]}$$
・分散の演算$${V[aX]=a^2V[X]}$$

標本比率の期待値$${\boldsymbol{E[\hat{p}]}}$$の計算
標本比率$${\hat{p}=x/n}$$、二項分布の期待値$${E[x]=np}$$より、
$${E[\hat{p}]=E[x/n]=E[\frac{1}{n}x]=\frac{1}{n}E[x]=\frac{1}{n}np=p}$$

標本比率の分散$${\boldsymbol{V[\hat{p}]}}$$の計算
標本比率$${\hat{p}=x/n}$$、二項分布の分散$${V[x]=np(1-p)}$$より、
$${V[\hat{p}]=V[x/n]=V[\frac{1}{n}x]=(\frac{1}{n})^2V[x]=(\frac{1}{n})^2np(1-p)=\frac{p(1-p)}{n}}$$

標本比率の期待値と分散が求まりました。

■公式：標本比率の期待値
$${E[\hat{p}]=p}$$

■公式：標本比率の分散
$${V[\hat{p}]=\cfrac{p(1-p)}{n}}$$

二項分布の正規分布近似
標本サイズ$${n}$$が大きいとき、二項分布は近似的に正規分布に従います。
正規分布$${N(\mu, \sigma)}$$のパラメータについて、$${\mu}$$は標本比率の期待値$${E[\hat{p}]=p}$$、分散は標本比率の分散$${V[\hat{p}]=\frac{p(1-p)}{n}}$$です。
つまり、確率変数としての標本比率$${\boldsymbol{\hat{p}}}$$は近似的に正規分布$${\boldsymbol{N(p, \frac{p(1-p)}{n})}}$$に従います。

標準誤差における近似
標本サイズ$${n}$$が大きい場合、標本比率$${\hat{p}}$$が母比率$${p}$$に近づくという大数の法則を利用して、標本平均の分散の式に含まれる$${p}$$を$${\hat{p}}$$に置き換えて、標準誤差を求めます。
標準誤差$${=\sqrt{V[\hat{p}]}=\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}}$$です。

標準化
確率変数としての標準比率$${\hat{p}}$$を標準化します。
$${z}$$値は「（確率変数－平均）／標準偏差」です（$${Z=\frac{X-\mu}{\sigma}}$$）。
標本平均の期待値（平均）は$${p}$$、標準偏差には標準誤差$${\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}}$$を充てます。
$${z}$$値は$${\cfrac{\hat{p}-p}{\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}}}$$です。

確率の計算
確率$${P(|\hat{p}-p| \leq 0.05)}$$の確率変数を標準化しましょう。
$${z}$$値は$${\cfrac{\hat{p}-p}{\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}}}$$。
$${|\hat{p}-p|}$$を$${\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}}$$で割ると$${z}$$値にできます。

では計算します。

$$
\begin{align*}
P(|\hat{p}-p| \leq 0.05)&=P \left( \left|\cfrac{\hat{p}-p}{\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}} \right| \leq \cfrac{0.05}{\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}} \right)\\
\\
&=P \left(|z| \leq \cfrac{0.05}{\sqrt{\cfrac{0.52\times0.48}{100}}} \right)\\
\\
&=P(|z| \leq 1.00)\\
&=P(-1.00 \leq z \leq 1.00)\\
\end{align*}
$$

標準正規分布$${N(0,1)}$$の$${P(-1.00 \leq z \leq 1.00)}$$を確認します。
次の図の青い部分が相当します。

確率の全体である$${1}$$から、標準正規分布の上側確率表より取得した確率を差し引いて確率$${P(-1.00 \leq z \leq 1.00)}$$を求めます。
「上側確率」は、図の左側の白い領域$${z>1.00}$$が相当します。
右側の「下側確率」$${z>-1.00}$$は上側確率$${z>1.00}$$と等しいです。
つまり、２箇所の白い領域は上側確率の２倍である$${2\times P(z>1.00)}$$です。
したがって、確率$${P(-1.00 \leq z \leq 1.00)}$$は、$${1}$$から$${2\times P(z>1.00)}$$を差し引いて算出できます。

標準正規分布の上側確率表を確認しましょう。

上側確率$${P(z>1.00)}$$は赤い枠の部分より$${0.1587}$$であることが分かりました。
計算に戻ります。

$$
\begin{align*}
P(|\hat{p}-p| \leq 0.05)&=P(-1.00 \leq z \leq 1.00)\\
&=1-2\times P(z>1.00)　※上側確率の２倍\\
&=1-2\times0.1587　※標準正規分布の上側確率表より\\
&=0.6826
\end{align*}
$$

$${P(|\hat{p}-p \leq 0.05|)}$$は$${0.683}$$です。

100人のサンプルから得たX候補者の標本得票率（標本比率）$${\hat{p}=0.52}$$と母集団の真の得票率$${p}$$のズレが$${\pm 0.05}$$以内である確率が約$${68\%}$$ということでしょう。
接戦状態で$${0.05}$$のズレが当落に影響するとなると、この確率の大きさ（小ささ）の評価が大切になりそうです。

最後に解答の標準正規分布のグラフを再確認しましょう。

平均$${\mu=0}$$を中心にして左右対称です。
$${P(-1.00 < z < 1.00)}$$は、平均$${\mu=0}$$から左右に標準偏差$${\sigma=1}$$離れた区間を範囲にする領域です。
一般に$${1\sigma}$$区間と呼ばれます。
$${1\sigma}$$区間におさまる確率は約$${68\%}$$です。

実践する

二項分布のグラフを描画してみよう！

二項分布の確率質量関数をグラフに描いてみましょう！
$${Bin(10,0.5)}$$の確率$${P(X=x), x=0, 1, \cdots ,10}$$を確率質量関数$${\ _nC_x \ p^x \ (1-p)^{n-x}}$$に当てはめて計算してグラフ化するのです。
確率計算結果（表）およびグラフの参考例は、「知る」の「二項分布の確率」と「二項分布の可視化」の項に記載していますので、参考にしてください。

電卓・手作業で作成してみよう！

上述の方法で手作業で二項分布の確率質量関数のグラフを描いてみましょう！
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。

EXCELで作成してみよう！

データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。

二項分布のグラフの作成
二項分布の確率質量関数の値は、①計算式を組む方法と、②BINOM.DIST関数を使用する方法で取得できます。

①計算式を組む方法
確率質量関数$${f(x)=\ _nC_x \ p^x \ (1-p)^{n-x}}$$を計算式で組みます。

組み合わせ$${\ _nC_x}$$はCOMBIN関数で計算します。
「COMBIN(試行回数n, 成功回数x)」です。

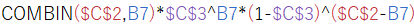
②BINOM.DIST関数を使用する方法
BINOM.DIST関数で二項分布の確率を計算します。

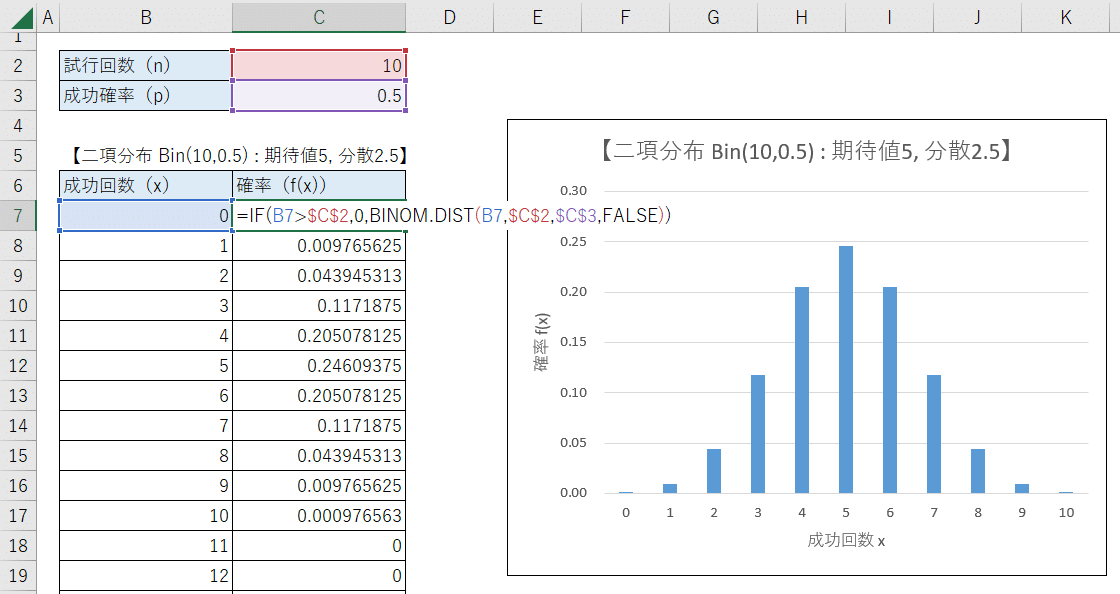
「BINOM.DIST(成功回数x, 試行回数n, 成功確率p, 確率質量関数FALSE)」です。

次のグラフができました。

試行回数ｎ、成功確率ｐをさまざまな値に変えてみて、二項分布の確率の変化を確認してみてくださいね。
次のグラフは試行回数100、成功確率0.6の例です。

EXCEL耳寄り情報
グラフのタイトルにセルの値を表示する方法をご紹介します。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

Pythonで作成してみよう！

プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。

今回は、二項分布の可視化に取り組みます。
設定を変更して、さまざまな二項分布のグラフの形状をご確認ください！

①インポート
scipy.statsのbinomで二項分布の確率質量関数、累積分布関数を取得します。

from scipy.stats import norm, binom
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline

②二項分布の確率質量関数のプロット
さまざまな二項分布の確率質量関数をプロットします。
scipy.statsのbinom.pmfで確率質量関数を取得します。
引数はデータx、試行回数、成功確率です。

paramsに二項分布のパラメータ：試行回数、成功確率を設定します。
x_min、x_maxにグラフの表示区間を設定します。

■例１

# 【設定】二項分布のパラメータを[試行回数, 成功確率], で繋いで指定
params = [[10, 0.5],]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = 0, 10

# 描画 binom.pmf(x, 試行回数, 成功確率)
x = range(x_min, x_max+1)
for n, p in params:
    plt.bar(x, binom.pmf(x, n, p), label=f'$Bin({n},{p})$')
plt.title('二項分布 確率質量関数')
plt.legend()

# plt.savefig('./binom_pmf_bar.png') # グラフ画像ファイルの保存
plt.show()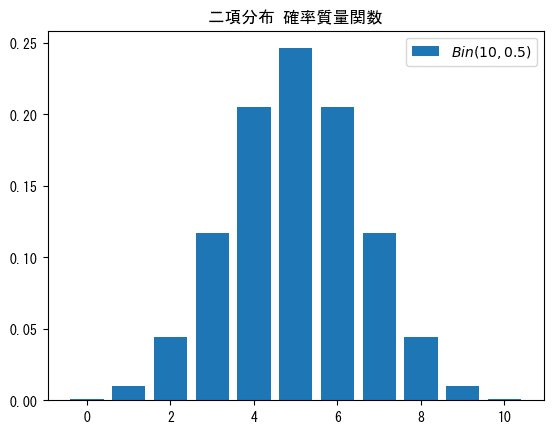

■例２

# 【設定】二項分布のパラメータを[試行回数, 成功確率], で繋いで指定
params = [[10, 0.5],]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = 0, 10

# 描画 binom.pmf(x, 試行回数, 成功確率)
x = range(x_min, x_max+1)
for n, p in params:
    plt.plot(x, binom.pmf(x, n, p), label=f'$Bin({n},{p})$')
plt.title('二項分布 確率質量関数')
plt.legend()

# plt.savefig('./binom_pmf1.png') # グラフ画像ファイルの保存
plt.show()

■例３

# 【設定】二項分布のパラメータを[試行回数, 成功確率], で繋いで指定
params = [
          [2, 0.5], [5, 0.5], [10, 0.5], [20, 0.5], [40, 0.5],  
          [60, 0.5], [80, 0.5], [100, 0.5],
         ]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = 0, 70

# 描画 binom.pmf(x, 試行回数, 成功確率)
x = range(x_min, x_max+1)
for n, p in params:
    plt.plot(x, binom.pmf(x, n, p), label=f'$Bin({n},{p})$')
plt.title('二項分布 確率質量関数')
plt.legend()

# plt.savefig('./binom_pmf2.png') # グラフ画像ファイルの保存
plt.show()

■例４

# 【設定】二項分布のパラメータを[試行回数, 成功確率], で繋いで指定
params = [
          [10, 0.1], [10, 0.2], [10, 0.3], [10, 0.4], [10, 0.5],
          [10, 0.6], [10, 0.7], [10, 0.8], [10, 0.9],
         ]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = 0, 10

# 描画 binom.pmf(x, 試行回数, 成功確率)
x = range(x_min, x_max+1)
for n, p in params:
    plt.plot(x, binom.pmf(x, n, p), label=f'$Bin({n},{p})$')
plt.title('二項分布 確率質量関数')
plt.legend()

# plt.savefig('./binom_pmf3.png') # グラフ画像ファイルの保存
plt.show()

③二項分布の累積分布関数のプロット
さまざまな二項分布の累積分布関数をプロットします。
scipy.statsのbinom.cdfで累積分布関数を取得します。
引数はデータx、試行回数、成功確率です。

paramsに二項分布のパラメータ：試行回数、成功確率を設定します。
x_min、x_maxにグラフの表示区間を設定します。

■例１

# 【設定】二項分布のパラメータを[試行回数, 成功確率], で繋いで指定
params = [[10, 0.5],]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = 0, 10

# 描画 binom.pmf(x, 試行回数, 成功確率)
x = range(x_min, x_max+1)
for n, p in params:
    plt.plot(x, binom.cdf(x, n, p), label=f'$Bin({n},{p})$')
plt.title('二項分布 確率質量関数')
plt.legend()

# plt.savefig('./binom_cdf1.png') # グラフ画像ファイルの保存
plt.show()

■例２

# 【設定】二項分布のパラメータを[試行回数, 成功確率], で繋いで指定
params = [
          [2, 0.5], [5, 0.5], [10, 0.5], [20, 0.5], [40, 0.5],  
          [60, 0.5], [80, 0.5], [100, 0.5],
         ]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = 0, 70

# 描画 binom.pmf(x, 試行回数, 成功確率)
x = range(x_min, x_max+1)
for n, p in params:
    plt.plot(x, binom.cdf(x, n, p), label=f'$Bin({n},{p})$')
plt.title('二項分布 確率質量関数')
plt.legend()

# plt.savefig('./binom_cdf2.png') # グラフ画像ファイルの保存
plt.show()

■例３

# 【設定】二項分布のパラメータを[試行回数, 成功確率], で繋いで指定
params = [
          [10, 0.1], [10, 0.2], [10, 0.3], [10, 0.4], [10, 0.5],
          [10, 0.6], [10, 0.7], [10, 0.8], [10, 0.9],
         ]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = 0, 10

# 描画 binom.pmf(x, 試行回数, 成功確率)
x = range(x_min, x_max+1)
for n, p in params:
    plt.plot(x, binom.cdf(x, n, p), label=f'$Bin({n},{p})$')
plt.title('二項分布 確率質量関数')
plt.legend()

# plt.savefig('./binom_cdf3.png') # グラフ画像ファイルの保存
plt.show()

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

おわりに

二項分布に寄り道して、標準正規分布の上側確率表を用いた正規分布の確率計算へと進みました。
試行回数$${n}$$が100くらいになると、二項分布のグラフの線がなめらかになり、正規分布に非常に似ていることを確認できたと思います。

この他にも、確率分布どうしでさまざまな繋がりを持っています。
例えば、幾何分布がある条件を満たすと二項分布やポアソン分布に近似します。

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事

この記事が気に入ったらサポートをしてみませんか？