
5-3 確率変数の関数の期待値 ~ 連続型確率変数の期待値をWebサイトで積分する
今回の統計トピック
期待値、確率変数の関数の期待値、積分計算に取り組みます。
欠かせない存在の積分計算、しかも強敵の積分計算。
今回は、Webサイトの計算ツールを活用して積分計算する方法を紹介いたします。
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
確率分布の分野
問3 確率変数の関数の期待値(1か月1人暮らしの水道使用量・料金)
試験実施年月
統計検定2級 2019年11月 問9(回答番号16)
問題
公式問題集をご参照ください。
解き方
題意
確率密度関数が$${f(x)}$$の連続型の確率変数$${X}$$があり、この確率変数$${X}$$の関数$${g(x)}$$の期待値$${E[g(x)]}$$を求めます。
連続型の確率変数$${X}$$は使用量であり、確率密度関数$${f(x)}$$は次のとおりです。
$$
f(x)=
\begin{cases}
\cfrac{1}{10} \left( 1-\cfrac{x}{20} \right) &(0 \leq x \leq 20)\\
0 &(x<0, x>20)
\end{cases}
$$
確率変数$${X}$$の関数$${g(X)}$$は料金であり、使用量に応じて次のように決まります。
$$
g(x)=
\begin{cases}
1000 &(0 \leq x<10)\\
1120 &(10 \leq x < 15)\\
1280 &(x \geq 15)
\end{cases}
$$
確率変数の関数の期待値
$${X}$$が確率変数のとき、確率変数$${X}$$の関数$${g(X)}$$も確率変数です。
関数$${g(X)}$$の期待値$${E[g(X)]}$$は、確率変数$${X}$$の確率密度関数$${f(x)}$$を用いて、次のように定義されます。
$$
E[g(X)] \equiv \displaystyle \int^{\infty}_{-\infty} g(x)f(x)dx
$$
この定義はざっくり、「確率変数の関数の期待値は、確率変数の関数の全ての値に確率の重み付けをした加重平均」です。
問題文の言葉で置き換えると、「料金の期待値は、料金の全ての値に使用量の確率の重み付けをした加重平均」ということになります。
可視化
料金の期待値は、次のように図示できます。
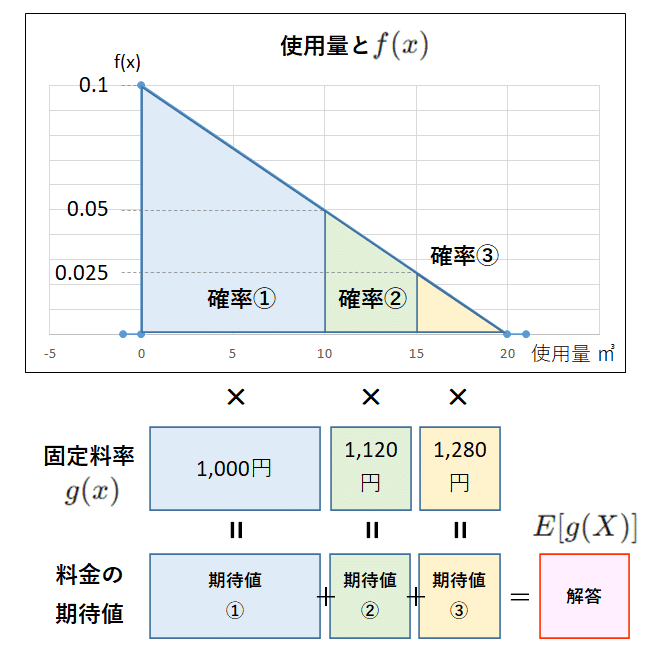
使用量$${X}$$は区間$${[0, 20]}$$で確率密度関数$${f(x)=1/10(1-x/20)}$$です。
式を展開すると$${f(x)=(-1/200)x+1/10}$$になるので、$${f(x)}$$のグラフは傾き$${-1/200}$$、切片$${1/10}$$の直線です。
$${X=0}$$のとき$${f(x)=1/10}$$、$${X=20}$$のとき$${f(x)=0}$$になります。
それでは解答に取り掛かりましょう。
まずは図形コースから。
図形コース
「使用量の確率」に「固定料率を掛けてから合算」して「料金の期待値」を計算してまいりましょう!
1.使用量の確率
使用量が発生する$${0 \leq x \leq 20}$$の範囲を考えます。
使用量$${f(x)}$$のグラフを紐解いて、料金が変わるポイント ①0~10㎥、②10~15㎥、③15~20㎥ に分けて、使用量のグラフの面積=確率を求めます。
■各ポイントのY軸$${f(x)}$$の値
問題文の$${f(x)=1/10(1-x/20)}$$に、ポイント$${x=0, 10, 15}$$を当てはめて、Y軸($${f(x)}$$)の値を計算します。
ポイント:$${x=0}$$㎥
$$
\begin{align*}
f(x)&=1/10 \times (1-0/20)\\
&=1/10\times(1-0)\\
&=1/10\times1\\
&=1/10\\
&=0.1\\
\end{align*}
$$
ポイント:$${x=10}$$㎥
$$
\begin{align*}
f(x)&=1/10 \times (1-10/20)\\
&=1/10\times(1-1/2)\\
&=1/10\times1/2\\
&=1/20\\
&=0.05\\
\end{align*}
$$
ポイント:$${x=15}$$㎥
$$
\begin{align*}
f(x)&=1/10 \times (1-15/20)\\
&=1/10\times(1-3/4)\\
&=1/10\times1/4\\
&=1/40\\
&=0.025\\
\end{align*}
$$
図のY軸の値 0.1、0.05、0.025が求まりました。
■確率①~③の計算
確率は面積で計算できます。
確率①の台形、確率②の台形、確率③の三角形の面積を計算しましょう。
図を反時計回りに回転して、グラフのY軸から上底と下底(底辺)、X軸から高さを取得します。
台形の面積=(上底+下底)× 高さ ÷ 2 です。
三角形の面積=底編 × 高さ ÷ 2 です。
・確率①
$$
確率①=(0.05+0.1)\times(10-0)\div2=0.75
$$
・確率②
$$
確率②=(0.025+0.05)\times(15-10)\div2=0.1875
$$
・確率③
$$
確率③=0.025\times(20-15)\div2=0.0625
$$
使用量の確率が求まりました。
確率①=0.75、確率②=0.1875、確率③=0.0625 です。
2.固定料率を掛けてから合算
使用量を0~10㎥、10~15㎥、15~20㎥ に場合分けして、固定料金 × 使用量の確率を求めてから合算して、料金の期待値$${E[g(X)]}$$を求めましょう。
使用量0~10㎥のとき
固定料金 1,000 円 × 確率① 0.75 = 750円使用量10~15㎥のとき
固定料金 1,120 円 × 確率② 0.1875 = 210円使用量15~20㎥のとき
固定料金 1,280 円 × 確率③ 0.0625 = 80円合算=料金の期待値$${E[g(X)]}$$
750円+210円+80円=1,040円
答えは 1,040円 です。
お疲れ様でした!

積分コース
問題文の確率密度関数$${f(x)}$$、料金の関数$${g(x)}$$、関数の期待値の定義を再掲します。
$$
\begin{align*}
f(x)&=
\begin{cases}
\cfrac{1}{10} \left( 1-\cfrac{x}{20} \right) &(0 \leq x \leq 20)\\
0 &(x<0, x>20)\\
\end{cases}\\
\\
g(x)&=
\begin{cases}
1000 &(0 \leq x<10)\\
1120 &(10 \leq x < 15)\\
1280 &(x \geq 15)
\end{cases}\\
\\
E[g(X)] &\equiv \displaystyle \int^{\infty}_{-\infty} g(x)f(x)dx
\end{align*}
$$
関数の期待値$${E[g(X)]}$$に$${f(x),g(x)}$$を当てはめて解きます。
$$
\begin{align*}
E([g(X)]&=\displaystyle \int^{\infty}_{-\infty} g(x)f(x)dx\\
\\
&=\displaystyle \int^{10}_{0} 1000\ \cfrac{1}{10} \left(1-\cfrac{x}{20} \right)dx
+\displaystyle \int^{15}_{10} 1120\ \cfrac{1}{10} \left(1-\cfrac{x}{20} \right)dx
+\displaystyle \int^{20}_{15} 1280\ \cfrac{1}{10} \left(1-\cfrac{x}{20} \right)dx\\
\\
&=\displaystyle \int^{10}_{0} 100 \left(1-\cfrac{x}{20} \right)dx
+\displaystyle \int^{15}_{10} 112 \left(1-\cfrac{x}{20} \right)dx
+\displaystyle \int^{20}_{15} 128 \left(1-\cfrac{x}{20} \right)dx\\
\\
&=\displaystyle 100 \int^{10}_{0} \left(1-\cfrac{x}{20} \right)dx
+\displaystyle 112 \int^{15}_{10} \left(1-\cfrac{x}{20} \right)dx
+\displaystyle 128\int^{20}_{15} \left(1-\cfrac{x}{20} \right)dx\\
\\
&=100 \left[x-\cfrac{x^2}{40} \right]^{10}_{0}
+112 \left[x-\cfrac{x^2}{40} \right]^{15}_{10}
+128 \left[x-\cfrac{x^2}{40} \right]^{20}_{15}\\
\\
&=100 \left(10-\cfrac{10^2}{40} \right)
+112 \left(15-\cfrac{15^2}{40} \right)-112 \left(10-\cfrac{10^2}{40} \right)
+128 \left(20-\cfrac{20^2}{40} \right)-128 \left(15-\cfrac{15^2}{40} \right)\\
\\
&=(100-112) \left(10-\cfrac{10^2}{40} \right)
+(112-128) \left(15-\cfrac{15^2}{40} \right)
+128 \left(20-\cfrac{20^2}{40} \right)\\
\\
&=-12 \left(\cfrac{400}{40}-\cfrac{100}{40} \right)
-16 \left(\cfrac{600}{40}-\cfrac{225}{40} \right)
+128 \left(\cfrac{800}{40}-\cfrac{400}{40} \right)\\
\\
&=-12 \times \cfrac{300}{40} -16 \times\cfrac{375}{40} +128 \times \cfrac{400}{40}\\
\\
&=-3 \times \cfrac{300}{10} -2 \times \cfrac{375}{5} +16 \times \cfrac{400}{5}\\
\\
&=-3 \times 30 -2 \times 75+16 \times 80\\
&=-90-150+1280\\
&=1040
\end{align*}
$$
答えは 1,040円 です。
お疲れ様でした!

定積分の計算の補足
$${F(x)}$$の微分が$${f(x)}$$になるとき、
$${f(x)=\left(1-\cfrac{x}{20} \right)}$$から$${F(x)}$$への操作は、
$${1 = 1 \times x^0 \rightarrow 1\times \cfrac{1}{1}x^1=x}$$
$${-\cfrac{x}{20} = -\cfrac{1}{20}x^1 \rightarrow -\cfrac{1}{20} \times\cfrac{1}{2}x^2= - \cfrac{1}{40}x^2=- \cfrac{x^2}{40}}$$
$${F(x)=x-\cfrac{x^2}{40}}$$になります。
解答
② 1,040円 です。
難易度 ふつう
・知識:連続型確率分布、確率変数の関数の期待値、積分
・計算力:数式組み立て(中)、数式計算(中)
・時間目安:2分
知る
おしながき
公式問題集の問題に接近してみましょう!
今回は、確率変数の関数の期待値に取り組みます!
さらっとね。
確率変数の関数の期待値
📕公式テキスト:2.5 期待値と分散(67ページ~)
期待値
確率変数$${X}$$の期待値$${E[X]}$$は「平均$${\mu}$$」です。
ざっくり「確率変数の期待値は、確率変数の全ての値に確率の重み付けをした加重平均」なのです。
例題
次のたからくじの期待値を求めてみましょう。
・1等 100万円の出る確率 0.01 %
・2等 1万円の出る確率 1 %
・3等 100円の出る確率 10 %
期待値は、
100万円×0.01%+1万円×1%+100円×10%
=100円+100円+10円
=210円
1枚200円だったら買いですね!

この例から期待値の定義を考えてみます。
確率変数$${X}$$は$${\{x_1=100万円,x_2=1万円,x_3=100円\}}$$の値を持ち、各確率$${f(x_i)}$$は$${\{f(x_1)=0.01\%,\ f(x_2)=1\%,\ f(x_3)=10\% \}}$$です。
期待値$${E[X]}$$は「確率変数の全ての値に確率の重み付けをした加重平均」ですので、$${E[X]=100万円\times 0.01\%+1万円\times 1\%+100円 \times 10\%}$$なのです。
期待値は、個々の確率変数の値と確率を掛けて足し上げる、こんな感じです。
期待値の定義式
■離散型の確率変数$${X}$$の場合
$$
E[X] \equiv \displaystyle \sum_i x_i f(x_i)=\mu
$$
■連続型の確率変数$${X}$$の場合
$$
E[X] \equiv \displaystyle \int^{\infty}_{-\infty} x\ f(x)\ dx=\mu
$$
意味合いは「確率変数の個々の値とその確率(または確率密度関数)を掛けて、足し上げる」です。
確率変数の関数の期待値
確率密度関数が$${f(x)}$$の確率変数$${X}$$があって、この確率変数$${X}$$に関数$${g(X)}$$があるとします。
この確率変数$${X}$$の関数$${g(X)}$$も確率変数になります。
確率変数$${g(X)}$$なのです。
公式問題集では、確率変数$${X}$$が使用量、確率変数の関数$${g(X)}$$が料金でした。
確率確率の関数=料金の期待値$${E[g(X)]}$$は、使用量$${X}$$の確率密度関数$${f(x)}$$と固定料率$${g(x)}$$に基づいて、面積計算/積分計算を行って算出しました。
期待値の定義式のうち、確率変数に相当する$${X}$$と$${x}$$の箇所を$${g(X)}$$と$${g(x)}$$に置き換えると、「確率変数の関数の期待値の定義式」になります。
確率変数の関数$${\boldsymbol{g(X)}}$$の期待値の定義式
■離散型の確率変数$${X}$$の場合
$$
E[g(X)] \equiv \displaystyle \sum_i g(x_i) f(x_i)
$$
■連続型の確率変数$${X}$$の場合
$$
E[g(X)] \equiv \displaystyle \int^{\infty}_{-\infty} g(x)\ f(x)\ dx
$$
期待値の定義式への当てはめ
今回の公式問題集のように確率関数の区間が複数ある場合は、その区間ごとに$${g(x)f(x)}$$を記述するような感じになります。
再掲します。
$$
\begin{align*}
f(x)&=
\begin{cases}
\cfrac{1}{10} \left( 1-\cfrac{x}{20} \right) &(0 \leq x \leq 20)\\
0 &(x<0, x>20)\\
\end{cases}\\
\\
g(x)&=
\begin{cases}
1000 &(0 \leq x<10)\\
1120 &(10 \leq x < 15)\\
1280 &(x \geq 15)
\end{cases}\\
\end{align*}
$$
この式から、確率変数$${X}$$は次の区間を取ることが分かります。
$$
x < 0,\ 0 \leq x < 10,\ 10 \leq x < 15,\ 15 \leq x \leq 20,\ 20 < x
$$
各区間ごとに期待値の定義式にざっくり当てはめてみましょう。
$$
\begin{align*}
E[g(X)]&=\displaystyle \int^{\infty}_{-\infty}g(x)f(x)dx\\
\\
&=\displaystyle \int^{0}_{-\infty} 0 \times 0 \ dx = 0\\
\\
&+\displaystyle \int^{10}_{0} 1000\ \cfrac{1}{10}\left( 1-\cfrac{x}{20} \right) \ dx\\
\\
&+\displaystyle \int^{15}_{10} 1120\ \cfrac{1}{10}\left( 1-\cfrac{x}{20} \right) \ dx\\
\\
&+\displaystyle \int^{20}_{15} 1280\ \cfrac{1}{10}\left( 1-\cfrac{x}{20} \right) \ dx\\
\\
&+\displaystyle \int^{\infty}_{20} 0 \times 0 \ dx = 0\\
\end{align*}
$$
(区間の境目の厳密さは・・・・・、ということで!)

定積分$${\boldsymbol{\int^b_a}}$$の計算
数学的な説明や学習は他のサイトにお願いいたします。ぺこり。
ここでは、積分計算をしてくれるサイトを紹介します!
期待値の式を組み立てることができれば、あとはネットにお任せなのです!

マイクロソフト社の数学ソルバー
画面はこんな感じ。
「数学の問題を入力」に積分の式を入力します。

$${\int}$$のボタンなどを利用して、積分の計算式を入力しました。
「解」ボタンをクリックして答えを見てみましょう。
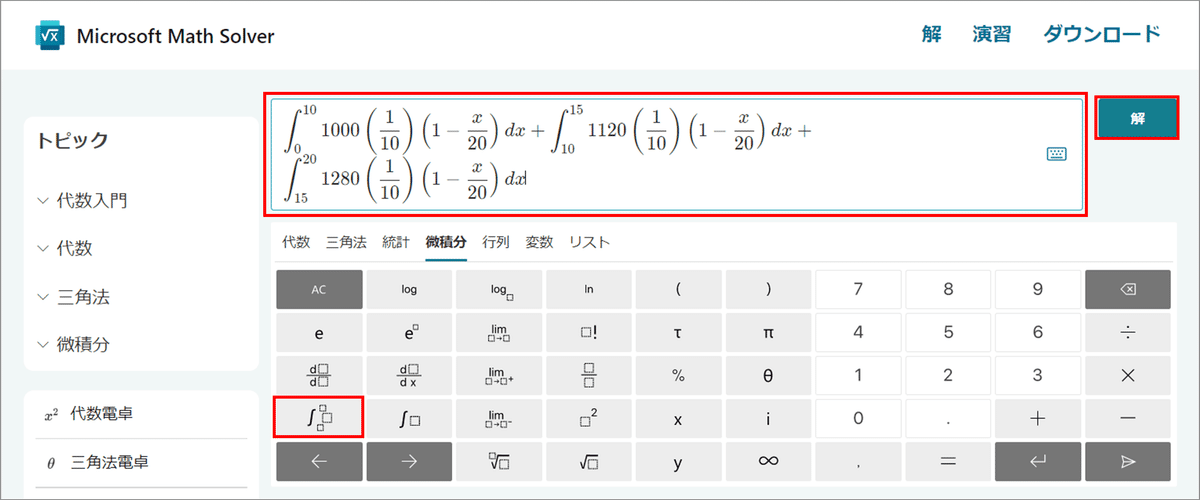
ご明算です!

マイクロソフト社のブラウザ「エッジ」を用いると、Webサイトの数式をドラッグするだけで計算することができるようです(記事執筆時点ではプレビュー版)。
wikibooksさん掲載の数式を利用して実験しましょう。
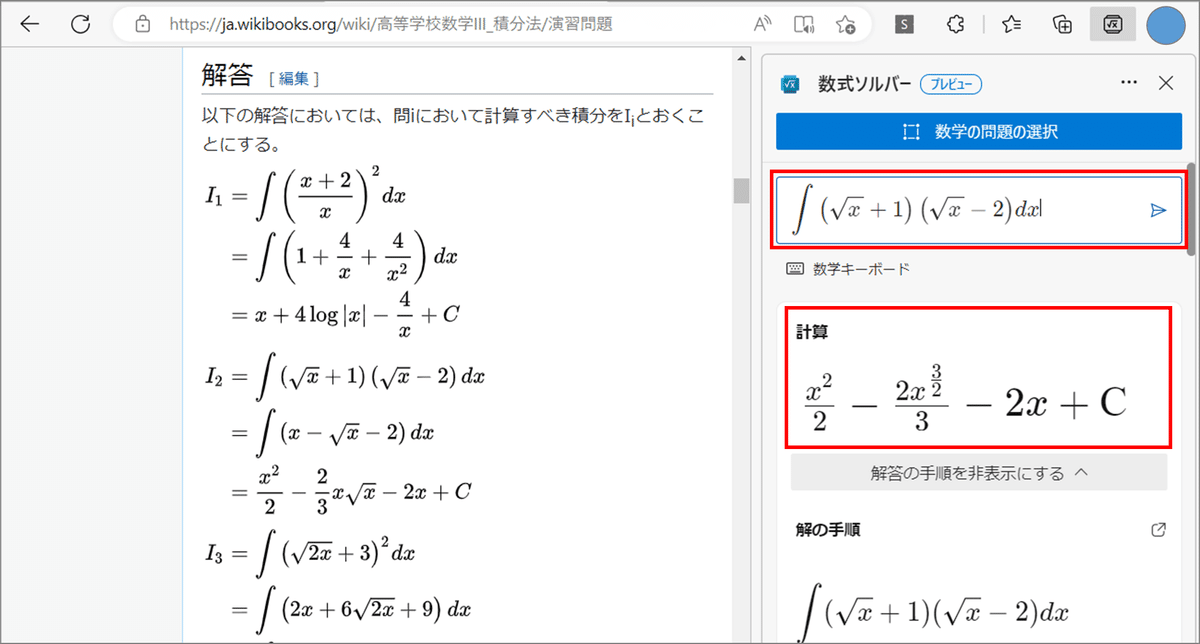
エッジに「数式ソルバー」(右側)を表示して「数学の問題の選択」を指定すると、Webサイトの画面がグレーになります。
ここで、数式の範囲をドラッグで指定すると・・・

数式(画像)を読み取って、計算結果を「計算」欄に表示します!
しかも「解の手順」の解説付き!
本来的には自らの手で積分の計算ができるようになることが望ましいのですが、ハードルが高い場合もあります。
ひとまず計算機を利用して「積分に慣れる」のもアリの時代ですよね!
「期待値の式の組み立てができるようになる」ところから始めましょう!
実践する
今回はお休みです。
公式問題集の問題を解いてみましょう!
電卓・手作業で作成してみよう!
今回はお休みです。
EXCELで作成してみよう!
今回はお休みです。
EXCELサンプルファイルのダウンロード
今回はファイル提供はありません。
Pythonで作成してみよう!
今回はお休みです。
Pythonサンプルファイルのダウンロード
今回はファイル提供はありません。
おわりに
確率・統計の分野では積分が活躍します。
連続型の確率分布について、確率密度関数$${f(x)}$$を手がかりにして、累積分布関数$${F(x)}$$・確率$${P(X>n)}$$・期待値$${E[X]}$$・分散$${V[X]}$$などなど、さまざまな計算に積分を用います。
サクッと計算できるコツを見つけたいものです・・・。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
この記事が気に入ったらサポートをしてみませんか?
