5-2 正規確率の計算 ～ 正規分布の確率密度関数を可視化して確率計算する

今回の統計トピック

正規分布の確率を計算します。
確率変数を標準化して、標準正規分布の上側確率表を利用します！
あわせて、さまざまな平均と分散（標準偏差）の正規分布のグラフ描画に取り組みます。

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

日本統計学会公式認定　統計検定　2級　公式問題集［CBT対応版］

問題を解く

---

📘公式問題集のカテゴリ

確率分布の分野
問2 正規確率の計算（データ無し）

試験実施年月
統計検定2級 2019年6月 問11（回答番号20）

問題

公式問題集をご参照ください。

解き方

題意
「正規分布の標準化」と「標準正規分布の上側確率表」を用いて正規分布の確率を計算する問題です。

正規分布の標準化
機械学習の前処理でおなじみの「標準化」(Standardization)。
正規分布$${N(\mu, \sigma^2)}$$に従う確率変数$${X}$$の標準化は、次の式で実施します。

$$
Z=(X-\mu)/\sigma
$$

この式は、確率変数$${X}$$から平均$${\mu}$$を差し引いて、標準偏差$${\sigma}$$で割ることで、標準化することを表しています。
標準化によって変換先の確率変数$${Z}$$は、平均$${0}$$、分散$${1}$$の正規分布$${N(0, 1)}$$に従います。

正規分布$${N(0, 1)}$$を標準正規分布と呼びます。
「確率変数$${Z}$$は標準正規分布に従う」、「確率変数$${Z \sim N(0,1)}$$」と表現します。

標準化と確率計算と可視化
問題文の正規分布と確率を可視化しましょう。

確率変数$${X}$$は、平均$${\mu=2}$$、分散$${\sigma^2=9}$$の正規分布$${N(2, 9)}$$に従います。
標準偏差$${\sigma=\sqrt{\sigma^2}=\sqrt{9}=3}$$です。
また、求める確率は$${P(-1< X \leq 4)}$$です。
正規分布$${N(2,9)}$$のグラフの青い領域に相当します。

この確率の確率変数$${X}$$の部分を$${Z=(X-\mu)/\sigma}$$にて標準化しましょう。

$$
\begin{align*}
P(-1< X \leq 4)&=P \left(\cfrac{-1-\mu}{\sigma} < \cfrac{X-\mu}{\sigma} \leq \cfrac{4-\mu}{\sigma}\right)\\
  \\
&=P \left(\cfrac{-1-2}{3} < Z \leq \cfrac{4-2}{3}\right)\\
  \\
&=P \left(-1 < Z \leq \cfrac{2}{3} \right)
\end{align*}
$$

標準正規分布と確率を可視化しましょう。
標準正規分布$${N(0,1)}$$の確率$${P(-1 < Z \leq 2/3)}$$は図の青い領域に相当します。

上側確率を見つける
青い領域は、全事象の確率$${P(\Omega)=1}$$から、白い領域「確率変数$${Z \leq-1,\quad Z > 2/3}$$」を差し引いて、求めることができます。

$$
\begin{align*}
P(-1< X \leq 4)&= P \left(-1 < Z \leq \cfrac{2}{3} \right)\\
  \\
&=1-P(Z \leq -1) -  P \left(Z \geq \cfrac{2}{3} \right)\\
\end{align*}
$$

$${P(Z \leq -1)}$$について考えます。
標準正規分布は平均$${\mu=0}$$を頂点として左右対称の分布です。
次の図の白い領域を確認しましょう。

左側の白い領域は確率変数$${Z \leq -1}$$の確率$${P(Z \leq -1)}$$です。
右側の白い領域は確率変数$${Z \geq 1}$$の確率$${P(Z \geq 1)}$$です。
両方の白い領域の面積は等しいです。
つまり、$${P(Z \leq -1)=P(Z \geq 1)}$$です。

$$
\begin{align*}
P(-1< X \leq 4)&=1-P(Z \leq -1) -  P \left(Z \geq \cfrac{2}{3} \right)\\
  \\
&=1-P(Z \geq 1) -  P \left(Z \geq \cfrac{2}{3} \right)\\
\end{align*}
$$

上側確率に変換できました。
上側確率は、次の図の白い領域に相当します。
確率変数$${Z=1}$$の上側の確率、$${Z=2/3}$$の上側の確率です。

$${P(Z \geq 1)}$$と$${P (Z \geq 2/3 )}$$は標準正規分布の上側確率表で近似値を得ることができます。

標準正規分布の上側確率表の見方
「標準正規分布の上側確率表」は、標準正規分布の横軸である確率変数$${Z}$$の値「$${z}$$値$${=u}$$」のときの上側確率$${Q(u)}$$を表します。

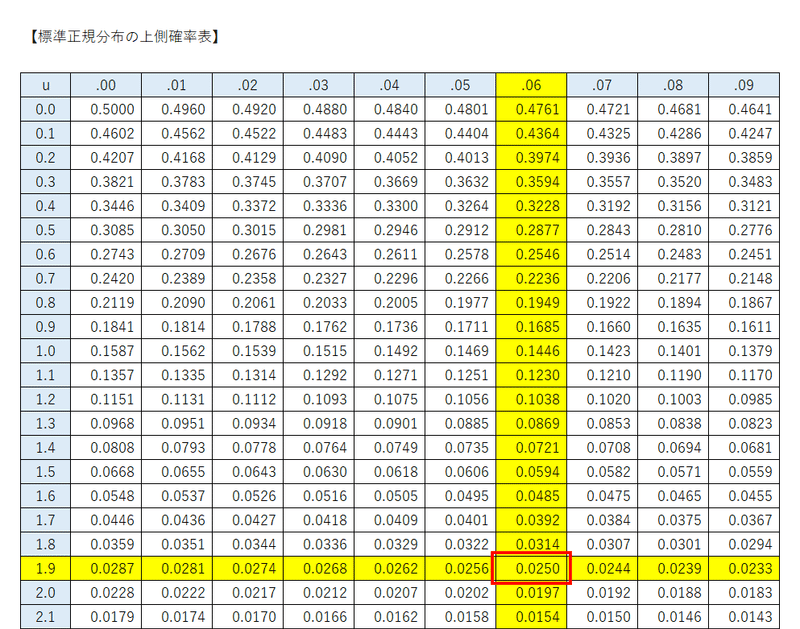
$${z}$$値$${u=1.96}$$を例にとって、上側確率表を確認してまいりましょう。
$${z}$$値を示す「表の行と列」に注目します。
行が「一の位．小数点第一位の$${1.9}$$」、列が「小数点第二位の$${0.06}$$」を表し、合体して $${u=1.96}$$ です。
行と列の交わる部分に上側確率$${Q(1.96)=0.0250}$$を表示しています。
$${z}$$値$${u=1.96}$$の上側確率は$${0.025=2.5\%}$$です。

$${z}$$値$${=1}$$の上側確率$${P(Z \geq 1)}$$と、$${z}$$値$${=2/3}$$の上側確率$${P(Z \geq 2/3)}$$を表から取得しましょう。

■$${z}$$値$${=1}$$の上側確率$${P(Z \geq 1)}$$
表より$${0.1587}$$です。

■$${z}$$値$${=2/3}$$の上側確率$${P(Z \geq 2/3)}$$
$${2/3=0.666 \cdots}$$なので、$${z}$$値が$${0.66}$$から$${0.67}$$の間に上側確率が存在します。

公式問題集と同じように、線形補間してみます。
$${0.2546+(0.2514-0.2546) \times 2/3=0.25246\cdots \fallingdotseq 0.2525}$$
上側確率$${P(Z \geq 2/3)}$$は$${0.2525}$$です。

総仕上げ
取得した上側確率を次の式に当てはめて確率を求めましょう。

$$
\begin{align*}
P(-1< X \leq 4)&=1-P(Z \geq 1) -  P \left(Z \geq \cfrac{2}{3} \right)\\
&=1-0.1587-0.2525=0.5888\\
&\fallingdotseq0.59\\
\end{align*}
$$

答えは$${P(-1< X \leq 4)=0.59}$$です。

まとめ

前回記事5-1の定積分付きグラフで確率を確認してみましょう。

確かに、正規分布$${N(2,9)}$$の確率$${P(-1< X \leq 4)}$$は$${0.589}$$です。
正規分布に従う確率変数を標準化しても確率は変わらないのです。

解答

⑤ 0.59 です。

難易度　ふつう

・知識：正規分布、標準化、標準正規分布の上側確率表
・計算力：数式組み立て（中）、数式計算（低）
・時間目安：2分

知る

---

おしながき

公式問題集の問題に接近してみましょう！
今回は、正規分布の確率計算と可視化に取り組みます！
確率分布界のキングのような存在の「正規分布」に迫ります！

正規分布

📕公式テキスト：2.8.2 正規分布（77ページ～）

正規分布の形状
正規分布の確率密度関数は平均$${\mu}$$（ミュー）を中心にして、左右対称の「釣り鐘」「ベル」の形状をしています。
次の図は平均$${\mu=1}$$、分散$${\sigma^2=4=2^2}$$の正規分布$${N(1, 2^2)}$$の確率密度関数$${f(x)}$$を表しています。

正規分布は平均$${\mu}$$と分散$${\sigma^2}$$で確率密度関数$${f(x)}$$が決まります。

■平均$${\mu}$$
平均$${\mu}$$の変化によって横軸をスライドします。
釣り鐘の形状は変わりません。

■分散$${\sigma^2}$$
分散$${\sigma^2}$$の変化によって峰の高さと裾の緩急が定まります。
分散$${\sigma^2}$$の値が小さい時、峰は高くなり、裾の変化が急です。
分散$${\sigma^2}$$の値が大きい時、峰は低くなり、裾の変化が緩やかです。

正規分布の確率密度関数
正規分布の確率密度関数は次のとおりです。

$$
f(x)=\cfrac{1}{\sqrt{2\pi \sigma^2}} \ \exp \left\{-\cfrac{(x-\mu)^2}{2\sigma^2} \right\} \quad (-\infty < x < \infty)
$$

正規分布の性質１：変換
確率変数$${X}$$が正規分布$${N(\mu,\sigma^2)}$$に従うとき、$${aX+b}$$は正規分布$${N(a\mu+b, a^2\sigma^2)}$$に従います。

$${aX+b}$$の平均と分散
・平均$${E[aX+b]}$$は$${aE[X]+E[b]=a\mu+b}$$です。
・分散$${V[aX+b]}$$は$${a^2V[X]=a^2\sigma^2}$$です。

正規分布の性質２：標準化
上述の変換を応用します。
確率変数$${X}$$が正規分布$${N(\mu,\sigma^2)}$$に従うとき、$${Z=(X-\mu)/\sigma}$$は標準正規分布$${N(0, 1)}$$に従います。

$${(X-\mu)/\sigma}$$の平均と分散
・平均$${E[(X-\mu)/\sigma]}$$は$${\frac{1}{\sigma} E[X-\mu]=E[X] / \sigma -\mu / \sigma= \mu / \sigma - \mu / \sigma=0}$$です。
・分散$${V[(X-\mu)/\sigma]}$$は$${\frac{1}{\sigma^2} V[X-\mu]=\frac{1}{\sigma^2} V[X] =\frac{1}{\sigma^2} \sigma^2=1}$$です。

正規分布の性質３：正規分布の再生性
確率変数$${X}$$と$${Y}$$が独立に正規分布$${N(\mu_X,\sigma^2_X)}$$、$${N(\mu_Y,\sigma^2_Y)}$$に従うとき、$${X+Y}$$は正規分布$${N(\mu_X+\mu_Y, \sigma^2_X+\sigma^2_Y)}$$に従います。
独立の条件があるので、平均も分散も足し算の関係が成立します。

標準正規分布の上側確率
「正規分布に従う確率変数$${X}$$」を「標準正規分布に従う確率変数$${Z}$$」に変換する主な目的は、標準正規分布の上側確率表を利用して確率を算出することにある、そんな気がします。

標準正規分布の上側確率表の利用方法

1. 確率変数$${X}$$を標準化して、$${z}$$値$${u}$$を求めます。

2. 標準正規分布の上側確率表は、$${z}$$値$${u}$$よりも大きい確率変数$${Z}$$における確率$${Q(u)=P(Z>u)}$$を記載しています。

3. $${z}$$値$${u}$$の値を表の行・列にあてはめて、確率$${Q(u)}$$を得ます。

（例）$${z}$$値$${u=1.96}$$のとき、確率$${Q(x)=0.0250}$$です。
※この$${z}$$値$${u=1.96 \rightarrow }$$確率$${Q(x)=0.025=2.5\%}$$はよく使います。

■$${z}$$値$${u}$$がマイナスの場合
マイナスを絶対値（正の値）に変換して上側確率表を見ます。

■$${z}$$値$${u}$$の区間両端が正の場合
２つの$${z}$$値$${u}$$の上側確率を取得して差し引きして確率を求めます。

実践する

---

正規分布のグラフを描画してみよう！

正規分布の確率密度関数をグラフに描いてみましょう！
EXCELで作成した「標準正規分布の上側確率表」と「標準正規分布の確率密度関数表」を用いて、標準正規分布の確率をグラフに起こすのです。

EXCELで標準正規分布の上側確率表を作成する方法は、次のサイトの情報を参考にいたしました。
ありがとうございました！

標準正規分布表（片側／両側）の見方とエクセルで作る方法をわかりやすく | 物流業界の歩き方標準正規分布表（片側／両側）の見方とエクセルで作る方法をわかりやすく | 物流業界の歩き方

EXCELファイルのダウンロード
こちらのリンクから「標準正規分布の上側確率表」EXCELファイルをダウンロードできます。

標準正規分布の上側確率表.xlsx

57.4 KB

ファイルダウンロードについて

ダウンロード

電卓・手作業で作成してみよう！

上述の方法でデータを取得して、手作業で標準正規分布の確率密度関数のグラフを描いてみましょう！
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。

標準正規分布の確率密度関数の表の「u」列の値を横軸に、「.00」列の値を縦軸にプロットすると、グラフの右側が完成します。
「u」列の値をマイナスにして（-1を掛ける）プロットすると、グラフの左側が完成します。

EXCELで作成してみよう！

データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。

正規分布のグラフの作成
正規分布の確率密度関数の値は「NORM.DIST」関数で取得できます。
引数には、NORM.DIST（xの値，平均，標準偏差，FALSE：確率密度関数）を設定します。
次のサンプルは、平均50、分散144（標準偏差12）の正規分布$${N(50, 12^2)}$$について、 B7セルから始まる x の値 0～100 に対して、C7セル以降で確率密度関数の値を計算しています。

EXCELサンプルファイルには、次のパターンの正規分布のグラフを例示しています。
数字を変更して、さまざまな正規分布の形状を確認してみましょう！

■標準正規分布

■平均の値を変えて複数比較

■分散の値を変えて複数比較

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

5-2_正規確率の計算.xlsx

69 KB

ファイルダウンロードについて

ダウンロード

Pythonで作成してみよう！

プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。

今回は、正規分布の可視化に取り組みます。

①インポート
scipy.statsのnormで正規分布の確率密度関数、累積分布関数を取得します。

import numpy as np
from scipy.stats import norm
from scipy.integrate import quad
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline

②正規分布の確率密度関数のプロット
さまざまな正規分布の確率密度関数をプロットします。
scipy.statsのnorm.pdfで確率密度関数を取得します。
引数は データx、平均、標準偏差です。

paramsに正規分布のパラメータ：平均、標準偏差を設定します。
x_min、x_maxにグラフの表示区間を設定します。

■例１

# 【設定】正規分布のパラメータを[平均, 標準偏差], で繋いで指定
params = [[0, 1],]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = -4, 4

# 描画 norm.pdf(x, 平均, 標準偏差)
x = np.linspace(x_min, x_max, 1000)
for mu, stddev in params:
    plt.plot(x, norm.pdf(x, mu, stddev), label=f'$N({mu},{stddev}^2)$')
plt.title('正規分布 確率密度関数')
plt.legend()

# plt.savefig('./norm_pdf1.png') # グラフ画像ファイルの保存
plt.show()

出力イメージ

■例２

# 【設定】正規分布のパラメータを[平均, 標準偏差], で繋いで指定
params = [[-1, 1], [0, 1], [1, 1], [5, 1], [10, 1]]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = -6, 16

# 描画 norm.pdf(x, 平均, 標準偏差)
x = np.linspace(x_min, x_max, 1000)
for mu, stddev in params:
    plt.plot(x, norm.pdf(x, mu, stddev), label=f'$N({mu},{stddev}^2)$')
plt.title('正規分布 確率密度関数')
plt.legend()

# plt.savefig('./norm_pdf2.png') # グラフ画像ファイルの保存
plt.show()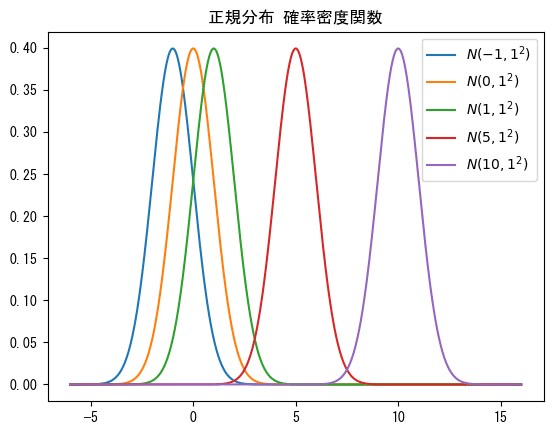

出力イメージ

■例３

# 【設定】正規分布のパラメータを[平均, 標準偏差], で繋いで指定
params = [[0, 1], [0, 3], [0, 5], [0, 10], [0, 20]]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = -50, 50

# 描画 norm.pdf(x, 平均, 標準偏差)
x = np.linspace(x_min, x_max, 1000)
for mu, stddev in params:
    plt.plot(x, norm.pdf(x, mu, stddev), label=f'$N({mu},{stddev}^2)$')
plt.title('正規分布 確率密度関数')
plt.legend()

# plt.savefig('./norm_pdf3.png') # グラフ画像ファイルの保存
plt.show()

出力イメージ

■例４

# 【設定】正規分布のパラメータを[平均, 標準偏差], で繋いで指定
params = [
          [1, 2], [2, 3], [3, 4], [4, 5], [5, 6], [6, 7], 
          [7, 8], [8, 9], [9, 10], [10, 11], [11, 12], [12, 13], 
         ]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = -20, 50

# 描画 norm.pdf(x, 平均, 標準偏差)
x = np.linspace(x_min, x_max, 1000)
for mu, stddev in params:
    plt.plot(x, norm.pdf(x, mu, stddev), label=f'$N({mu},{stddev}^2)$')

plt.title('正規分布 確率密度関数')
plt.legend()

# plt.savefig('./norm_pdf4.png') # グラフ画像ファイルの保存
plt.show()

出力イメージ

③正規分布の累積分布関数のプロット
さまざまな正規分布の累積分布関数をプロットします。
scipy.statsのnorm.cdfで累積分布関数を取得します。
引数は データx、平均、標準偏差です。

paramsに正規分布のパラメータ：平均、標準偏差を設定します。
x_min、x_maxにグラフの表示区間を設定します。

■例１

# 【設定】正規分布のパラメータを[平均, 標準偏差], で繋いで指定
params = [
          [0, 1], 
         ]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = -4, 4

# 描画 norm.cdf(x, 平均, 標準偏差)
x = np.linspace(x_min, x_max, 1000)
for mu, stddev in params:
    plt.plot(x, norm.cdf(x, mu, stddev), label=f'$N({mu},{stddev}^2)$')
plt.title('正規分布 累積分布関数')
plt.legend()

# plt.savefig('./norm_cdf1.png') # グラフ画像ファイルの保存
plt.show()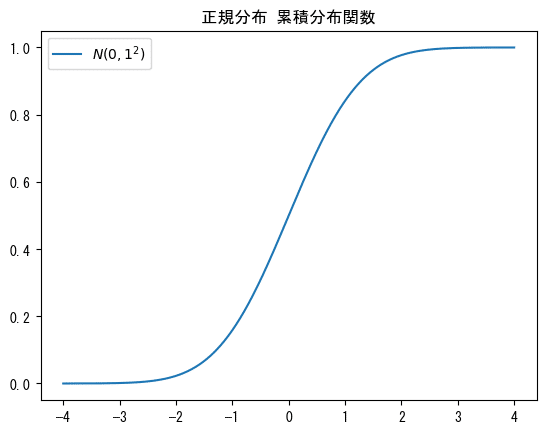

出力イメージ

■例２

# 【設定】正規分布のパラメータを[平均, 標準偏差], で繋いで指定
params = [[-1, 1], [0, 1], [1, 1], [5, 1], [10, 1]]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = -6, 16

# 描画 norm.cdf(x, 平均, 標準偏差)
x = np.linspace(x_min, x_max, 1000)
for mu, stddev in params:
    plt.plot(x, norm.cdf(x, mu, stddev), label=f'$N({mu},{stddev}^2)$')
plt.title('正規分布 累積分布関数')
plt.legend()

# plt.savefig('./norm_cdf2.png') # グラフ画像ファイルの保存
plt.show()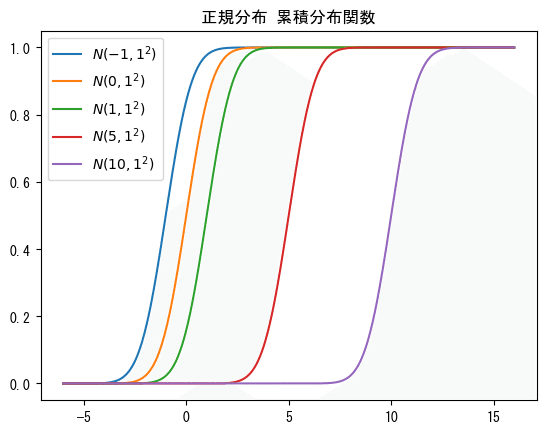

出力イメージ

■例３

# 【設定】正規分布のパラメータを[平均, 標準偏差], で繋いで指定
params = [[0, 1], [0, 3], [0, 5], [0, 10], [0, 20]]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = -50, 50

# 描画 norm.cdf(x, 平均, 標準偏差)
x = np.linspace(x_min, x_max, 1000)
for mu, stddev in params:
    plt.plot(x, norm.cdf(x, mu, stddev), label=f'$N({mu},{stddev}^2)$')
plt.title('正規分布 累積分布関数')
plt.legend()

# plt.savefig('./norm_cdf3.png') # グラフ画像ファイルの保存
plt.show()

出力イメージ

■例４

# 【設定】正規分布のパラメータを[平均, 標準偏差], で繋いで指定
params = [
          [1, 2], [2, 3], [3, 4], [4, 5], [5, 6], [6, 7], 
          [7, 8], [8, 9], [9, 10], [10, 11], [11, 12], [12, 13], 
         ]

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = -20, 50

# 描画 norm.cdf(x, 平均, 標準偏差)
x = np.linspace(x_min, x_max, 1000)
for mu, stddev in params:
    plt.plot(x, norm.cdf(x, mu, stddev), label=f'$N({mu},{stddev}^2)$')
plt.title('正規分布 累積分布関数')
plt.legend()

# plt.savefig('./norm_cdf4.png') # グラフ画像ファイルの保存
plt.show()

出力イメージ

④確率計算と確率密度関数のプロット：共通処理の定義
積分計算とグラフ表示の共通処理をPython関数で定義します。

# xの型に応じて関数case_f(x)の処理を変える
def f(x, mu, stddev):
    if isinstance(x, (int, float)): # xがint型、float型の場合、map処理が不要
        fx = def_f(x, mu, stddev)
    else:
        fx = list(map(lambda z: def_f(z, mu, stddev), x))
    return fx

# 【設定】確率密度関数f(x)の定義
def def_f(x, mu, stddev):
    fx = norm.pdf(x, loc=mu, scale=stddev)
    return fx 

#  積分計算、関数・積分区分のプロット
def f_plot(x_min, x_max, a, b, mu, stddev):

    # 関数の値の取得
    x = np.linspace(x_min, x_max, 1000)  # 変数 X の値を取得
    y = f(x, mu, stddev)                 # 関数f(x)の値を取得

    # 積分区間[a,b]の定積分計算
    result = quad(f, a, b, limit=1000, args=(mu, stddev))

    # 関数の描画
    plt.plot(x, y)

    # 積分区間[a,b]の領域の描画
    y0 = 0                               # y=0
    x_ab = np.linspace(a, b, 1000)       # 積分区間[a,b]の変数Xの値を取得
    y_ab = f(x_ab, mu, stddev)           # 積分区間[a,b]の関数f(x)の値を取得
    plt.fill_between(x_ab, y_ab, y0,     # 面を塗りつぶす描画
                     alpha=0.1) 
    plt.hlines(y0, x_min, x_max, lw=0.5, # y=0の水平線の描画 x_min≦X≦x_max
               color='gray', ls='--')
    plt.hlines(y0, a, b, lw=0.5)         # y=0の水平線の描画 a≦X≦b
    plt.vlines(a, y0, y_ab[0], lw=0.5)   # x=aの垂直線の描画
    plt.vlines(b, y0, y_ab[-1], lw=0.5)  # x=bの垂直線の描画

    plt.title(
              f'正規分布 $N({mu:.2f}, {stddev:.2f}^2)$\n'
              f'確率 $\int^b_a f(x)dx={result[0]:.3f}$\n'
              f'$a={a:.2f},\ b={b:.2f}$'
             )

    plt.tight_layout()
#     plt.savefig('./norm_pdf_int.png') # グラフ画像ファイルの保存
    plt.show()
    
    return result

⑤確率計算と確率密度関数のプロット：処理の実行
設定値を変えることで、さまざまな正規分布の確率密度関数と確率計算を実行できます。
・正規分布の平均と標準偏差：mu、stddev
・グラフの表示区間：x_min、x_max
・確率計算区間（積分区間）：a、b

# 【設定】正規分布の平均と標準偏差
mu, stddev = 10, 10

# 【設定】確率密度関数f(x)の描画区間[x_min,x_max]
x_min, x_max = -50, 75

# 【設定】定積分の積分区間[a,b]
a, b = 12, 70

# 処理の実行
integrate_result = f_plot(x_min, x_max, a, b, mu=mu, stddev=stddev)

出力イメージ

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

5-2_正規確率の計算.ipynb

517 KB

ファイルダウンロードについて

ダウンロード

---

おわりに

ようやく正規分布の問題がやってきました。
正規分布と標準正規分布は統計（検定２級）の様々なシーンで登場します。
末永いおつきあいになりそうです。

最後までお読みいただきまして、ありがとうございました。

---

のんびり統計シリーズの記事

次の記事

前の記事

目次