
5-7 X-Yの確率計算 ~ 正規分布に従う確率変数の線形結合と可視化
今回の統計トピック
確率変数の変数変換/線形結合と正規分布の関係に迫ります!
期待値・分散の演算も取り組みますよー!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
確率分布の分野
問7 X-Yの確率計算(電気料金)
試験実施年月
統計検定2級 2018年6月 問8(回答番号16)
問題
公式問題集をご参照ください。
解き方
数式が並びます。何卒、何卒。

題意
確率変数の線形結合と正規分布の再生性をベースにして、正規分布に従う独立の確率変数どうしの差の確率を求めます。
そして正規分布の確率と言えば、確率変数を標準化して標準正規分布の上側確率表を活用します。
問題を要約します。
ある月の電気料金は確率変数です。
ある月について、今年の電気料金を確率変数$${X}$$、昨年の電気料金を確率変数$${Y}$$とすると、差の$${X-Y}$$も確率変数です。
確率変数$${X}$$と$${Y}$$は独立に正規分布$${N(4000, 500^2)}$$に従います。
このときに確率変数$${X-Y}$$が$${800}$$円以上になる確率$${P(X-Y \geq 800)}$$を求めます。

正規分布の再生性
2つの確率変数が独立に正規分布に従うとき、2つの確率変数の和も正規分布に従います。
この性質を正規分布の再生性と呼びます。
確率変数$${X}$$と$${Y}$$が独立に正規分布$${N(\mu_X,\ \sigma^2_X)}$$、$${N(\mu_Y,\ \sigma^2_Y)}$$に従うとき、確率変数$${X+Y}$$は正規分布$${N( \mu_X + \mu_Y ,\ \sigma^2_X + \sigma^2_Y )}$$に従います。

確率変数の線形結合と正規分布
2つの確率変数が独立に正規分布に従うとき、2つの確率変数の線形結合も正規分布に従います。
確率変数$${X}$$と$${Y}$$が独立に正規分布$${N(\mu_X,\ \sigma^2_X)}$$、$${N(\mu_Y,\ \sigma^2_Y)}$$に従うとき、$${X}$$と$${Y}$$の1次結合(線形結合)である$${aX+bY}$$($${a,\ b}$$は定数)は、正規分布$${N(a \mu_X + b \mu_Y,\ a^2 \sigma^2_X+b^2 \sigma^2_Y)}$$に従います。

確率変数$${\boldsymbol{X-Y}}$$の従う正規分布
では、問題の各値を正規分布の線形結合の計算式に当てはめましょう。
確率変数$${X}$$と$${Y}$$は独立に正規分布$${N(4000,\ 500^2)}$$に従います。
平均$${\mu_X=\mu_Y=4000}$$、分散$${\sigma^2_X=\sigma^2_Y=500^2}$$です。
2つの確率変数の差は線形結合であり、$${X-Y=1X+(-1)Y}$$なので、$${a=1,\ b=-1}$$です。
$${X-Y}$$が従う正規分布$${N(a \mu_X + b \mu_Y,\ a^2 \sigma^2_X+b^2 \sigma^2_Y)}$$に各値を当てはめます。
$${N(1 \times 4000 +(-1) \times 4000,\ 1^2 \times 500^2 +(-1)^2 \times 500^2)}$$となり、$${N(0,\ 500^2 \times 2)}$$です。
$${X-Y}$$が従う正規分布は、平均$${\mu_{X-Y}=0}$$、分散$${\sigma^2_{X-Y}=500^2 \times 2}$$ということが分かりました。

標準化
確率変数$${X}$$の標準化と言えば$${Z=\cfrac{X-\mu}{\sqrt{\sigma^2}}}$$です。
これを確率変数$${X-Y}$$のケースに当てはめます。
確率$${P(X-Y \geq 800)}$$のかっこの中を平均$${\mu_{X-Y}=0}$$、分散$${\sigma^2_{X-Y}=500^2 \times 2}$$を使って、標準化します。
$$
\begin{align*}
P(X-Y \geq 800) &=P \left( \cfrac{(X-Y) - \mu_{X-Y} }{ \sqrt{ \sigma^2_{X-Y} }} \geq \cfrac{800 - \mu_{X-Y}}{ \sqrt{ \sigma^2_{X-Y}} } \right)\\
\\
&=P \left( Z \geq \cfrac{800-0}{\sqrt{500^2 \times 2}} \right)\\
\\
&=P \left( Z \geq \cfrac{800}{\sqrt{500^2} \times \sqrt{2}} \right)\\
\\
&=P \left( Z \geq \cfrac{800}{500\sqrt{2}} \right)\\
\\
&\approx P(Z \geq 1.13)
\end{align*}
$$
標準正規分布$${N(0,1)}$$のグラフを確認しましょう。
$${z}$$値$${=1.13}$$は垂直点線の部分にあたります。
$${P(Z \geq 1.13)}$$は概ね青塗りの領域の面積です。
$${z}$$値$${=1.13}$$の右側=上側の面積が求める確率です。

$${z}$$値が$${1.13}$$以上となる上側確率を「標準正規分布の上側確率表」から見つけましょう。

$${z}$$値$${=1.13}$$の上側確率$${P(Z \geq 1.13)}$$は$${0.1292}$$です。
答えは 0.129 です。
Pythonのscipy.statsで計算した確率も 0.1292 になりました。

ちなみに、標準化する前の正規分布$${N(0, 500^2 \times 2)}$$のグラフは次のようになります。

若干、確率の値が異なるのは、標準化の際に$${\cfrac{800}{500\sqrt{2}} \approx1.13}$$の計算で端数を丸めたことが影響しています。
標準正規分布の上側確率表から求めた確率が「近似値」であることを意識する必要がありそうです。
解答
③ 0.129 です。
難易度 ふつう
・知識:確率変数の線形結合、正規分布の再生性
・計算力:数式組み立て(中)、数式計算(低)
・時間目安:1分
知る
おしながき
公式問題集の問題に接近してみましょう!
今回は、正規分布に従う確率変数の変数変換・線形結合にトライしてまいりましょう!
期待値・分散の演算
📕公式テキスト:2.9.2 共分散と相関係数の「コメント」(84ページ~)
実験/シミュレート
最初に問題$${X-Y}$$に出てきた正規分布を実験をします!
独立に正規分布$${N(4000,\ 500^2)}$$に従う確率変数$${X}$$と$${Y}$$の差$${X-Y}$$が正規分布$${N(0,\ 500^2 \times 2)}$$に従うのかを、Pythonでシミュレートします。
次の4パターンについてそれぞれ、乱数を10,000,000個生成してヒストグラムをプロットします。
【4つのパターン】
$${X}$$:正規分布$${N(4000,\ 500^2)}$$に従う乱数
$${Y}$$:正規分布$${N(4000,\ 500^2)}$$に従う乱数
$${X-Y}$$:「$${X}$$の乱数の値」$${-}$$「$${Y}$$の乱数の値」
$${U}$$:正規分布$${N(0,\ 500^2 \times 2)}$$に従う乱数
「3.$${X-Y}$$」と「4.$${U}$$」が一致する場合、「独立に正規分布$${N(4000,\ 500^2)}$$に従う確率変数$${X}$$と$${Y}$$の線形結合$${X-Y}$$が正規分布$${N(0,\ 500^2 \times 2)}$$に従う」ことを確認できます。
そして次の図が4つの乱数をプロットした結果です。

グリーンの「3.$${X-Y}$$」と 赤枠の「4.$${U}$$」がピッタリ一致しています!
両方のヒストグラムは平均$${\mu=0}$$を中心にして、きれいなベル型の正規分布に似た形状を示しています。
「独立に正規分布$${N(4000,\ 500^2)}$$に従う確率変数$${X}$$と$${Y}$$の線形結合$${X-Y}$$が正規分布$${N(0,\ 500^2 \times 2)}$$に従う」ことを確認できました!
コードは「Pythonで作成してみよう!」で紹介いたします。

期待値と分散の演算
期待値と分散の演算の重要な公式に触れます。
ここでは、特定の確率分布に限定しない、確率変数全般のお話になります。
確率変数$${X,\ Y}$$について、期待値を$${E[X]}$$、分散を$${V[X]}$$、共分散を$${\mathrm{Cov}[X,\ Y]}$$と表します。
まず1~2つの確率変数バージョンです。
$${X}$$と$${Y}$$は確率変数、$${a,\ b,\ c}$$は定数です。
$${aX+c}$$と$${aX+bY+c}$$について考えます。
■期待値の演算の公式
$${E[aX+c]=aE[X]+c}$$
$${E[aX+bY+c]=aE[X]+bE[Y]+c}$$
■分散の演算の公式
$${V[aX+c]=a^2V[X]}$$
$${V[aX+bY+c]=a^2V[X]+b^2V[Y]+2ab \mathrm{Cov}[X, Y]}$$
$${V[aX+bY+c]=a^2V[X]+b^2V[Y]}$$($${X}$$と$${Y}$$が独立の場合)
次に3つ以上の確率変数バージョンです。
$${n}$$個の確率変数$${X_1, X_2, \cdots , X_n}$$について考えます。
■期待値の演算の公式
$${E[X_1+X_2+\cdots + X_n]=E[X_1]+E[X_2]+\cdots +E[X_n]}$$
■分散の演算の公式
$${V[X_1+X_2+\cdots + X_n]=V[X_1]+V[X_2]+\cdots +V[X_n]+2\displaystyle \sum^{n-1}_{i=1} \sum^n_{j=i+1} \mathrm{Cov}[X_i,\ X_j]}$$
最後に複数の確率変数が独立に平均・分散の同一の確率分布に従う場合について、確率変数の和と平均を考えます。
$${n}$$個の確率変数$${X_1, X_2, \cdots , X_n}$$、平均$${\mu}$$、分散$${\sigma^2}$$、確率変数の平均$${\bar{X}}$$で表します。
■期待値の演算の公式
$${E[X_1+X_2+\cdots + X_n]=n\mu}$$
$${E[\bar{X}]=\mu}$$
■分散の演算の公式
$${V[X_1+X_2+\cdots + X_n]=n\sigma^2}$$
$${V[\bar{X}]=\cfrac{\sigma^2}{n}}$$
簡単なまとめ
期待値と分散の演算をざっくりまとめます。
「確率変数の係数をかっこの外に出すとき、期待値は係数の値そのまま、分散は係数の二乗の値になる」という感じです。
ここまでは、特定の確率分布に限定しない、一般的な期待値・分散のお話でした。
次に正規分布に話を移します。
正規分布と変数変換・線形結合
📕公式テキスト:2.8.2 正規分布(77ページ~)
正規分布に従う確率変数$${X,\ Y}$$について、変数変換$${aX+c}$$、線形結合$${aX+bY+c}$$を行うとき、$${aX+c}$$、$${aX+bY+c}$$も正規分布に従います。
正規分布を変数変換(1次変換)を施しても正規分布、線形結合を施しても正規分布なのです。
正規分布の性質1:変数変換(1次変換)
確率変数$${X}$$が正規分布$${N(\mu,\sigma^2)}$$に従うとき、$${aX+c}$$は正規分布$${N(a\mu+c,\ a^2\sigma^2)}$$に従います。
$${aX+c}$$の平均と分散
・平均$${E[aX+c]}$$は$${aE[X]+E[c]=a\mu+c}$$です。
・分散$${V[aX+c]}$$は$${a^2V[X]=a^2\sigma^2}$$です。
標準化はこの変換変換の性質に基づきます。
正規分布の性質2:線形結合
確率変数$${X}$$と$${Y}$$が独立に正規分布$${N(\mu_X,\ \sigma^2_X)}$$、$${N(\mu_Y,\ \sigma^2_Y)}$$に従うとき、$${aX+bY+c}$$は正規分布$${N(a\mu_X+b\mu_Y+c,\ a^2\sigma^2_X + b^2\sigma^2_Y)}$$に従います。
$${aX+bY+c}$$の平均と分散
・平均$${E[aX+bY+c]}$$は
$${aE[X]+bE[Y]+E[c]=a\mu_X+b \mu_Y +c}$$です。
・分散$${V[aX+bY+c]}$$は
$${a^2V[X]+b^2V[Y]=a^2\sigma^2_X + b^2\sigma^2_Y}$$です。
例題を用いて、確率変数の変換と正規分布の変化に迫ります!
例題1
確率変数$${X}$$が正規分布$${N(10, 4)}$$に従うとき、$${2X+3}$$が従う正規分布の平均と分散を計算しましょう。
【解き方】
確率変数$${X}$$が従う正規分布は、平均$${E[X]=\mu=10}$$、分散$${V[X]=\sigma^2=4}$$です。
変数変換の式より、平均と分散を得ます。
・平均$${E[2X+3]=2E[X]+3=2\times10+3=23}$$
・分散$${V[2X+3]=2^2V[X]=4 \times 4=16}$$
答えは、平均$${=23}$$、分散$${=16}$$ です。
グラフを見てみましょう。

例題2
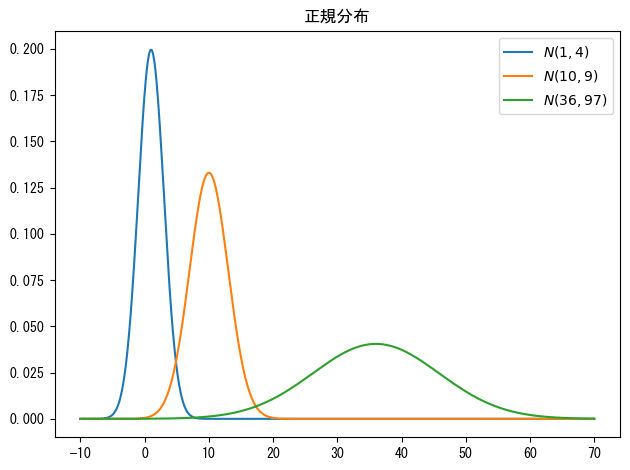
確率変数$${X}$$と$${Y}$$が独立に正規分布$${N(1, 4)}$$、$${N(10, 9)}$$に従うとき、$${2X+3Y+4}$$が従う正規分布の平均と分散を計算しましょう。
【解き方】
確率変数$${X}$$が従う正規分布は、平均$${E[X]=\mu_X=1}$$、分散$${V[X]=\sigma^2_X=4}$$です。
確率変数$${Y}$$が従う正規分布は、平均$${E[Y]=\mu_Y=10}$$、分散$${V[Y]=\sigma^2_Y=9}$$です。
線形結合の式より、平均と分散を得ます。
・平均$${E[2X+3Y+4]=2E[X]+3E[Y]+4=2\times1+3\times 10 + 4=36}$$
・分散$${V[2X+3Y+4]=2^2V[X]+3^2V[Y]=4 \times 4 + 9 \times 9=97}$$
答えは、平均$${=36}$$、分散$${=97}$$ です。
グラフを見てみましょう。
【次回予告】
次回記事「5-8 線形な変数変換、共分散、相関係数」にて、変数変換を深掘りします!
実践する
正規分布の変数変換・線形結合を体感してみよう!
確率変数の変換を行うときに正規分布がどのように変化するか、平均と分散を計算したり、グラフを描いて形状を確認しましょう!
EXCELを活用して、グラフの形状、平均・分散をシミュレートしていきましょう!
Pythonコードでサクサク図表化しましょう。
電卓・手作業で作成してみよう!
「知る」の例題1、例題2を解いてみましょう。
また、「EXCELで作成してみよう!」の内容を参照しつつ、確率変数を変換/結合して、平均・分散を計算したり、正規分布のグラフを描いてみましょう。
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。
EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。
データシートの紹介
変数変換$${aX+c}$$と線形結合$${aX+bY+c}$$のデータシートを作成しました。
変数変換$${aX+c}$$のデータシート(抜粋)は次のような雰囲気です。
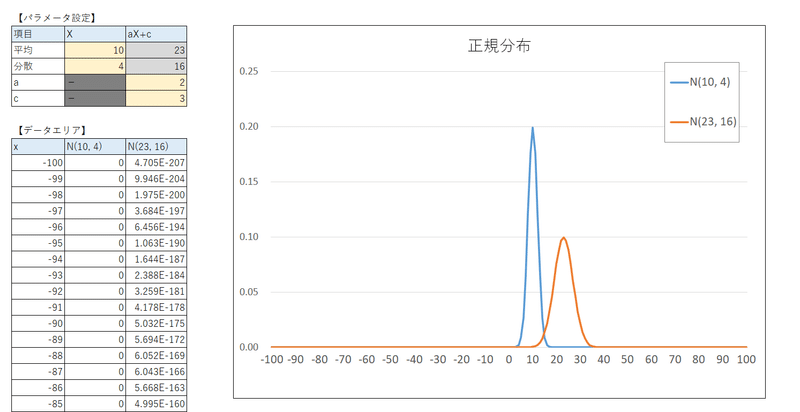
黄色のセルにパラメータの設定値を入力します。
確率変数$${X}$$が従う正規分布の平均と分散、$${aX+c}$$の$${a,\ c}$$の値です。
パラメータの値を変えてみましょう。
例えば次のようにパラメータを変更します。

パラメータの値に連動して【データエリア】正規分布の確率密度関数の値(NORM.DIST関数)が変わり、グラフの描画も変わります。

確率変数$${X}$$のデータ値$${x}$$は$${-100}$$から$${100}$$まで用意しました。
線形結合$${aX+bY+c}$$のデータシート(抜粋)は次のような雰囲気です。
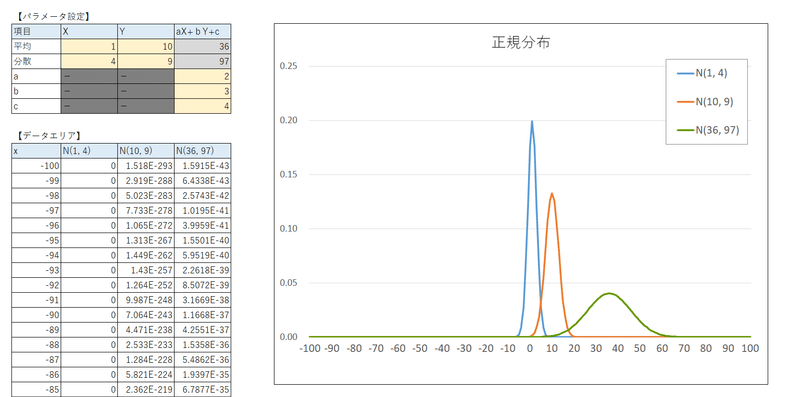
黄色のセルにパラメータ設定値を入力します。
確率変数$${X}$$が従う正規分布の平均と分散、確率変数$${Y}$$が従う正規分布の平均と分散、$${aX+bY+c}$$の$${a,\ b,\ c}$$の値です。
パラメータの設定値をいろいろ変えてみて、平均・分散・グラフの形状の変化を楽しんでくださいね。
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回は、「知る」の章で使用した図表のコードを紹介します。
ぜひパラメータを変更して、正規分布の形状と数値の変化をご堪能ください!
なお、正規分布の第2パラメータには分散ではなく「標準偏差」を用いています。
scipyの仕様に合わせています。
$${標準偏差=\sqrt{分散}}$$です。
①インポート
scipy.statsのnormを利用して、正規分布に従う乱数生成と確率密度関数・累積分布関数の値を取得します。
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline②X-Yの分布をプロットして確かめる
「実験/シミュレート」で使用したグラフを描画します。
norm.rvsで正規分布に従う乱数を生成します。
引数は norm.rvs( 平均, 標準偏差, 乱数生成数 )です。
コンピュータの負荷が高いようでしたら、その他の設定の「size」(乱数の生成数)の値を小さくしてください。
# 設定 確率変数X,Yの平均・標準偏差
x_mu, x_stddev = 4000, 500
y_mu, y_stddev = 4000, 500
# その他の設定
np.random.seed(3) # 乱数シード
size = 10000000 # 乱数の生成数
alp = 0.2 # グラフの透明度
# 乱数生成:確率変数X、確率変数Y、XとYの差、X-Yの分布に従う確率変数U
X = norm.rvs(x_mu, x_stddev, size=size)
Y = norm.rvs(y_mu, y_stddev, size=size)
subXY = X - Y
U = norm.rvs(x_mu-y_mu, np.sqrt(x_stddev**2+y_stddev**2), size=size)
# プロット
bins = np.linspace(-4000, 6000, 101)
plt.hist(X, bins=bins, histtype='bar', alpha=alp, ec='darkblue', label='X')
plt.hist(Y, bins=bins, histtype='step', label='Y')
plt.hist(subXY, bins=bins, histtype='bar', alpha=alp, ec='darkgreen', label='X-Y')
plt.hist(U, bins=bins, histtype='step', label='U')
plt.legend()
# plt.savefig('./hist1.png') # グラフ画像ファイルの保存
plt.show()
③正規分布のグラフ描画(z値の上側確率を表示)
設定欄の z値(この値の上側確率を算出)、表示区間[a, b]を変更して、さまざまな正規分布のグラフと上側確率を確認しましょう!
norm.pdfで正規分布の確率密度関数の値を取得します。
引数は norm.pdf( xデータ, 平均, 標準偏差 )です。
また上側確率を表示する目的で、norm.cdfで正規分布の累積分布関数の値(下側確率です)を取得します。
引数は norm.cdf( xデータ, 平均, 標準偏差 )です。
# 設定
z = 1.13 # z値
a, b = -4, 4 # 表示区間[a, b]
prob_disp = True # 確率を表示 True, 非表示 False
# 正規分布曲線の取得
mu, stddev = 0, 1 # 平均、標準偏差
x = np.linspace(a, b, 1001)
y = norm.pdf(x, loc=mu, scale=stddev)
# Z>zの曲線の取得
x_zb = np.linspace(z, b, 100)
y_zb = norm.pdf(x_zb, loc=mu, scale=stddev)
# 上側確率 P(Z>z)の計算 1-累積分布関数cdf
p = 1- norm.cdf(z, loc=mu, scale=stddev)
prob= f'$P(Z>{z}) \\approx {p:.4f}$'
# プロット
plt.plot(x, y, label=f'$N({mu},{stddev**2})$')
plt.fill_between(x_zb, y_zb, 0, alpha=0.2, label=f'$P(Z>{z})$')
plt.vlines(z, 0, max(y), ec='gray', lw=0.5, ls='--')
plt.hlines(0, a, b, ec='gray', lw=0.5, ls='--')
plt.text(z, 0, f'$z={z}$')
if not prob_disp:
prob=''
if (mu==0)&(stddev==1):
plt.title(f'標準正規分布 $N({mu},{stddev})$\n' + prob)
else:
plt.title(f'正規分布 $N({mu},{stddev**2:.1f})$\n' + prob)
plt.legend()
plt.tight_layout()
# plt.savefig('./norm1.png') # グラフ画像ファイルの保存
plt.show()
こちらのコードは標準化前の正規分布と上側確率のグラフを描画します。
設定の平均mu、標準偏差stddev、上側確率のx値xdata、表示区間[a, b]を変更して、正規分布の形状や上側確率の変化を確認できます。
# 設定
mu, stddev = 0, 500*np.sqrt(2) # 平均、標準偏差
xdata = 800 # 上側確率を求めるxの値
a, b = -2500, 2500 # 表示区間[a, b]
prob_disp = True # 確率を表示 True, 非表示 False
# 正規分布曲線の取得
x = np.linspace(a, b, 1001)
y = norm.pdf(x, loc=mu, scale=stddev)
# X>xの曲線の取得
x_xb = np.linspace(xdata, b, 100)
y_xb = norm.pdf(x_xb, loc=mu, scale=stddev)
# 上側確率 P(Z>z)の計算 1-累積分布関数cdf
p = 1- norm.cdf(xdata, loc=mu, scale=stddev)
prob= f'$P(X>{xdata}) \\approx {p:.4f}$'
# プロット
plt.plot(x, y, label=f'$N({mu},{stddev**2:.1f})$')
plt.fill_between(x_xb, y_xb, 0, alpha=0.2, label=f'$P(X>{xdata})$')
plt.vlines(xdata, 0, max(y), ec='gray', lw=0.5, ls='--')
plt.hlines(0, a, b, ec='gray', lw=0.5, ls='--')
plt.text(xdata, 0, f'$x={xdata}$')
if not prob_disp:
prob=''
if (mu==0)&(stddev==1):
plt.title(f'標準正規分布 $N({mu},{stddev})$\n' + prob)
else:
plt.title(f'正規分布 $N({mu},{stddev**2:.1f})$\n' + prob)
plt.legend()
plt.tight_layout()
# plt.savefig('./norm2.png') # グラフ画像ファイルの保存
plt.show()
④正規分布に従う確率変数Xの変数変換(aX+c)
設定の平均muX、標準偏差stddevX、関数aX+cのaとc、表示区間[u, v]を変更して、正規分布の形状の変化を確認できます。
# 設定
muX, stddevX = 10, 2 # 平均、標準偏差
a, c = 2, 3 # aX+c
u, v = -10, 50 # 表示区間[u, v]
# 変数変換の平均mu2と標準偏差stddev2の算出
muX2 = a * muX + c
stddevX2 = np.sqrt(a**2 * stddevX**2)
# 正規分布曲線の取得
x = np.linspace(u, v, 1001)
fxX = norm.pdf(x, loc=muX, scale=stddevX)
fxX2 = norm.pdf(x, loc=muX2, scale=stddevX2)
# プロット
plt.plot(x, fxX, label=f'$N({muX:.0f},{stddevX**2:.0f})$')
plt.plot(x, fxX2, label=f'$N({muX2:.0f},{stddevX2**2:.0f})$')
plt.title('正規分布')
plt.legend()
plt.tight_layout()
# plt.savefig('./norm3.png') # グラフ画像ファイルの保存
plt.show()
⑤正規分布に従う確率変数X,Yの線形結合(aX+bX+c)
確率変数XとYを取り扱います。
設定の平均muX, muY、標準偏差stddevX, stddevY、関数aX+bY+cのa, b, c、表示区間[u, v]を変更して、正規分布の形状の変化を確認できます。
# 設定
muX, stddevX = 1, 2 # 平均、標準偏差
muY, stddevY = 10, 3 # 平均、標準偏差
a, b, c = 2, 3, 4 # aX+bY+c
u, v = -10, 70 # 表示区間[u, v]
# 変数変換の平均muXYと標準偏差stddevXYの算出
muXY = a * muX + b * muY + c
stddevXY = np.sqrt(a**2 * stddevX**2 + b**2 * stddevY**2)
# 正規分布曲線の取得
x = np.linspace(u, v, 1001)
fxX = norm.pdf(x, loc=muX, scale=stddevX)
fxY = norm.pdf(x, loc=muY, scale=stddevY)
fxXY = norm.pdf(x, loc=muXY, scale=stddevXY)
# プロット
plt.plot(x, fxX, label=f'$N({muX:.0f},{stddevX**2:.0f})$')
plt.plot(x, fxY, label=f'$N({muY:.0f},{stddevY**2:.0f})$')
plt.plot(x, fxXY, label=f'$N({muXY:.0f},{stddevXY**2:.0f})$')
plt.title('正規分布')
plt.legend()
plt.tight_layout()
# plt.savefig('./norm4.png') # グラフ画像ファイルの保存
plt.show()
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
確率変数の変換はなかなかの強敵です。
記事で省略した「変換の公式の証明」を習得することで、変数変換の理解をいっそう深める(親交を深める)ことができるのかもしれません。
これらの証明は確率・統計を扱うさまざまなWebサイトで取り扱っているので、ぜひ、いろんなWebサイトを訪れてみてください。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
この記事が気に入ったらサポートをしてみませんか?
