「Pythonではじめる異常検知入門」を寄り道写経 ～ 第７章「異常検知の実践例」②One-Class SVM

第７章「異常検知の実践例」

書籍の著者　笛田薫 先生、江崎剛史 先生、李鍾賛 先生

---

この記事は、テキスト「Pythonではじめる異常検知入門」の第７章「異常検知の実践例」の 7-1-2 項および 7-1-3 項の「データが正規分布に従うことを仮定した異常検知」について、通称「寄り道写経」を取り扱います。

テキストのワインデータをお借りしてOne-Class SVM による異常検知を実践します！
ではテキストを開いて異常検知の旅に出発です🚀

ちなみに第５章も One-Class SVM で寄り道をしています。
よかったら覗いていってくださいね。

このシリーズは書籍「Pythonではじめる異常検知入門」（科学情報出版、「テキスト」と呼びます）の異常検知の理論・数式とPythonプログラムを参考にしながら、テキストにはプログラムの紹介が無いけれども気になったテーマ、または、テキストのプログラム以外の方法を試したいテーマを「実験的」にPythonコード化する寄り道写経ドキュメンタリーです。

はじめに

---

テキスト「Pythonではじめる異常検知入門」のご紹介

テキストは、2023年4月に発売された異常検知の入門書です。
数式展開あり、Python実装ありのテキストなのです。
Jupyter Notebook 形式のソースコードと csv 形式のデータは、書籍購入者限定特典として書籍掲載のURLからダウンロードできます。

Pythonではじめる異常検知入門 ―基礎から実践まで― (エンジニア入門シリーズ117) | 笛田 薫, 江崎 剛史, 李 鍾賛 |本 | 通販 | Amazon

引用表記

この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「Pythonではじめる異常検知入門－基礎から実践まで－」初版、著者 笛田薫／江崎剛史／李鍾賛、オーム社

記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます！

かわいいフリー素材集

第７章 異常検知の実践例

---

Jupyter Notebook 形式（拡張子 .ipynb）でPythonコードを書きます。

テキストのこの章では、次の３種類の異常検知をPythonで実践します。

① ホテリングの$${\boldsymbol{T^2}}$$法
・非時系列データが正規分布に従うと仮定する場合の異常検知
② One-Class SVM
・非時系列データが正規分布を従うと仮定しない場合の異常検知
③ 時系列データの異常検知
・残差が正規分布に従うと仮定する場合の異常検知

この記事は ② の非時系列データが正規分布に従うと仮定しない場合の異常検知の寄り道写経を行います
テキストが利用するデータを引用させていただき、実装方法やパラメータを変えて、One-Class SVMに近づきたいと考えています。

インポート

### インポート

# 数値・確率計算
import pandas as pd
import numpy as np

# 距離計算
from scipy.spatial import distance

# 機械学習
from sklearn.datasets import load_wine
from sklearn.preprocessing import StandardScaler
from sklearn.svm import OneClassSVM

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

Google Colab をご利用の場合は「描画」箇所を以下のように差し替えてください。

!pip install japanize_matplotlib
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns

データの読み込み

scikit-learn のデータセットに含まれる「wine」データセットを利用します。
UCI の機械学習リポジトリから取得することも可能です。

UCI Machine Learning Repository

### データの読み込み

# scikit-learnのwineデータセットを取得
wine = load_wine()
# 説明変数をデータフレーム化
df = pd.DataFrame(wine.data, columns=wine.feature_names)
# 目的変数をデータフレーム化
target = pd.DataFrame(wine.target, columns=['class'])
# 説明変数データの表示
print('df.shape: ', df.shape)
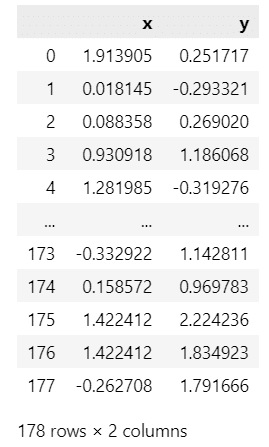
display(df.head())

【実行結果】
説明変数データは 13 説明変数、標本サイズ（行数）178です。

【利用する変数】
この記事では２つの説明変数「magnesium」「color_intensity」を用いて異常検知に取り組みます！

### 異常検知に用いる２変数を選択
data_2 = (df[['magnesium', 'color_intensity']].set_axis(['x', 'y'],axis=1))
print('data_2.shape: ', data_2.shape)
display(data_2.head())

【実行結果】
x は magnesium、y は color_intensity です。

データの可視化

散布図を描画します。
seaborn の regplot で作画した回帰直線付きの散布図です。
テキスト図7-4に相当します。

### MagnesiumとColor_intensityの散布図の描画
plt.figure(figsize=(5, 5))
sns.regplot(data=data_2, x='x', y='y', line_kws={'color': 'tomato'},
            scatter_kws={'color': 'lightblue','ec': 'tab:blue', 's': 80})
plt.grid(lw=0.5);

【実行結果】
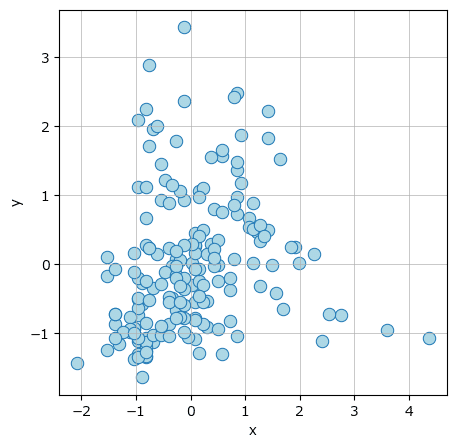
データは「Ｌ字型」の形状に見えます。
回帰直線が当てはまっていません。

データの標準化

scikit-learn の StandardScaler() を用いてデータを標準化します。
分母に不偏標準偏差を使わない点は、テキストで標準化に用いる scipy の zscore のデフォルト値（ddof=0）と同様です。

### データの標準化 scikit-learnのStandardScaler使用 ddof=0
scaler = StandardScaler()
data = pd.DataFrame(scaler.fit_transform(data_2), columns=data_2.columns)
display(data)

【実行結果】

標準化後のデータの散布図を seaborn で描画します。
回帰直線の表示は省略します。
テキスト図7-5に相当します。

### 標準化後のMagnesiumとColor_intensityの散布図の描画
plt.figure(figsize=(5, 5))
sns.scatterplot(data=data, x='x', y='y', s=80, color='lightblue', ec='tab:blue')
plt.grid(lw=0.5);

【実行結果】

One-Class SVM の学習

標準化後のデータを学習データにして、One-Class SVM の学習を行います。
One-Class SVM のパラメータにはテキストと異なる値を設定しました。

### ２変数x,yでOne-Class SVMで異常度を算出

# One-Class SVM分類器の設定
clf = OneClassSVM(nu=0.03, kernel='rbf', gamma=0.19)

# One-Class SVM分類器の学習
clf.fit(data)

# 学習データによるクラス予測 1:正常値、-1:外れ値
pred = clf.predict(data)

# 決定境界からの距離の算出 負は外れ値
score = clf.decision_function(data)

【実行結果】なし

学習データのうち、異常に分類されたデータの個数を確認します。

### 学習データのうち異常判定されるデータの個数
print('異常データの数: ', (pred == -1).sum())

【実行結果】
178 データ点の中から 7 点が異常判定されるモデルのようです。

正常／異常の分布を確認します。
decision_function にて算出した「決定境界からの距離」をスコアに見立てています。
テキスト図7-6に相当します。

### 異常スコア（決定境界からの距離）のヒストグラムの描画処理

# ビンを0.01間隔で設定
bins = np.arange(-0.14, 0.22, 0.01)
# 描画領域の設定
fig, ax = plt.subplots(figsize=(7, 4))
# 閾値の赤点線の描画
ax.axvline(color='tab:red', ls='--')
# 異常判定領域を薄赤色で塗りつぶし描画
ax.fill_between([-0.15, 0], 0, 44, color='lightpink', alpha=0.2)
# ヒストグラムの描画
sns.histplot(x=score, bins=bins, ec='white', ax=ax)
# 修飾
ax.set(xlabel='異常度（決定境界からの距離）', ylabel='頻度',
       xlim=(-0.15, 0.23), ylim=(0, 44), yticks=range(0, 48, 10))
ax.grid(lw=0.5);

【実行結果】
薄赤色のゾーンが「異常」です。

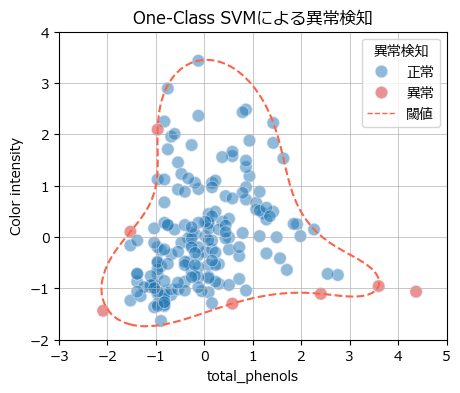
異常値の線引になる「決定境界」を示した散布図を描画します。
テキスト図7-7に相当します。

### 決定境界を示した散布図の描画

## 等高線用のx,y,zの値を設定
xx, yy = np.meshgrid(np.linspace(-3, 5, 100), np.linspace(-2, 4, 100))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

## 描画処理
# 描画領域の指定
fig, ax = plt.subplots(figsize=(5, 4))
# 決定境界（異常値の閾値）の描画
ax.contour(xx, yy, Z, levels=[0], colors='tomato', linwidths=1,
           linestyles='--')
# 散布図の描画
sns.scatterplot(x=data['x'], y=data['y'], hue=pred*-1, s=80, alpha=0.5,
                palette=['tab:blue', 'tab:red'], ec='lavender', ax=ax)
# 凡例
ax.plot([], [], color='tomato', lw=1, ls='--', label='決定境界')
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles=handles, labels=['正常', '異常', '閾値'], title='異常検知')
# 修飾
ax.set(xlabel='total_phenols', ylabel='Color intensity',
       title='One-Class SVMによる異常検知')
ax.grid(lw=0.5);

【実行結果】
決定境界（閾値）は丸めのテトラポッドに似てます。
異常値のうち、右下の１点は確かにデータの分布から離れていて「異常」と見てもいい感じがします。
その他の６点は閾値の近くに存在するので「異常」にするのは微妙？な感じがしないでもないです。

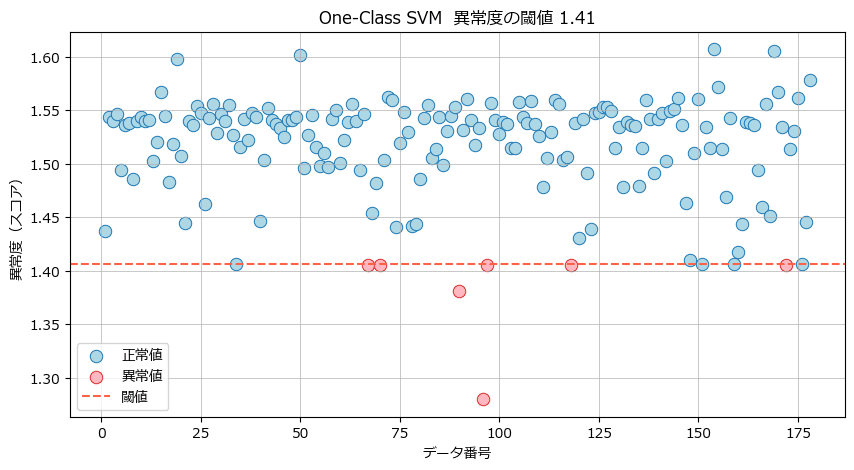
異常度に使えるスコアがもう１つあります。
score_samples で取得できるスコアです。
管理図ライクな図を描画してみましょう。

### 異常判別の描画

## 異常度（スコア）の算出 
score_samples = clf.score_samples(data)

## 描画処理
# 描画領域の指定
fig, ax = plt.subplots(figsize=(10, 5))
# 正常値の散布図の描画
query1 = pred >= 0
sns.scatterplot(x=np.where(query1)[0] + 1, y=score_samples[query1], s=80,
                color='lightblue', ec='tab:blue', ax=ax, label='正常値')
# 異常値の散布図の描画
query2 = pred < 0
sns.scatterplot(x=np.where(query2)[0] + 1, y=score_samples[query2], s=80,
                color='lightpink', ec='tab:red', ax=ax, label='異常値')
# 閾値の水平線の描画
ax.axhline(clf.offset_, color='tomato', ls='--', label='閾値')
# 修飾
ax.set_title(f'One-Class SVM  異常度の閾値 {clf.offset_[0]:.2f}')
ax.set(xlabel='データ番号', ylabel='異常度（スコア）')
ax.grid(lw=0.5)
ax.legend(loc='lower left');

【実行結果】
閾値の赤点線から離れているのは２点のようです。

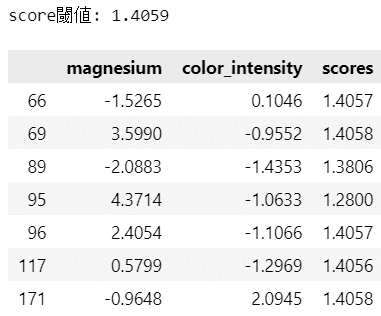
異常７点のデータの詳細を確認します。

### 異常値の詳細
print(f'score閾値: {clf.offset_[0]:.4f}')
scores = np.concatenate([data.values, score_samples.reshape(-1, 1)], axis=1)
anomaly_idx = np.where(pred < 0)[0]
pd.DataFrame(scores[anomaly_idx], index=anomaly_idx,
             columns=['magnesium', 'color_intensity', 'scores']).round(4)

【実行結果】
score の具体的な値から閾値との乖離のレベル感を把握できました。

ひとまずのまとめです。
いろいろありましたが、学習した結果で異常検知モデルを FIX（仕様凍結）します！

未知データの異常検知

未知データを作成して、異常検知してみましょう！

■ 未知データの作成

### 未知データの作成
data_new = np.array([[80, 7], [80, 5.5], [120, 2.5], [125, 2.5], [140, 10]])
print('未知データ:')
print(data_new)

【実行結果】
５つのデータを作成しました。

■ データの標準化
学習済みの標準化器「scaler」を用います。

### 未知データの標準化
data_new_ss = scaler.transform(data_new)
print('標準化後の未知データ:')
print(data_new_ss)

【実行結果】

■ 異常検知の実行
それでは！📯
未知データの異常検知を実行します！
学習済みの分類器「clf」を用います。

### 未知データの異常検知

# 学習済モデルclfによるクラス予測 1:正常値、-1:外れ値
pred_new = clf.predict(data_new_ss)
print('正常・異常ラベル　: ', pred_new)

# 決定境界からの距離の算出 負は外れ値
score_new = clf.decision_function(data_new_ss)
print('決定境界からの距離: ', score_new)

## 異常度（スコア）の算出
score_samples_new = clf.score_samples(data_new_ss)
print('スコア　　　　　　: ', score_samples_new)

【実行結果】
５つのデータの正常・異常ラベル、決定境界からの距離、スコアです。
異常ラベル＝－１が異常ですので、１、４、５番目の３つのデータが異常です！

■ 異常検知結果の確認
異常度を可視化しましょう。
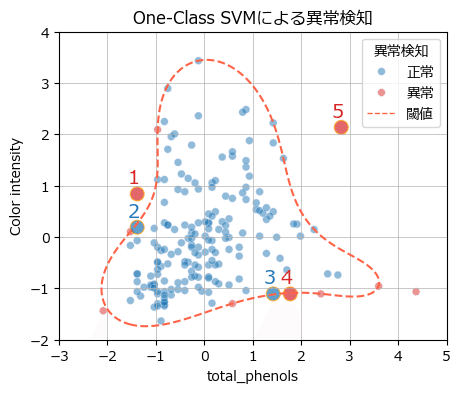
まずは決定境界を示した散布図の描画から。

### 決定境界を示した散布図の描画

# 描画領域の指定
fig, ax = plt.subplots(figsize=(5, 4))
# 決定境界（異常値の閾値）の描画
ax.contour(xx, yy, Z, levels=[0], colors='tomato', linwidths=1,
           linestyles='--')
# 学習データの散布図の描画
sns.scatterplot(x=data['x'], y=data['y'], hue=pred*-1, s=30, alpha=0.5,
                palette=['tab:blue', 'tab:red'], ec='lavender', ax=ax)
# 未知データの散布図の描画
sns.scatterplot(x=data_new_ss[:, 0], y=data_new_ss[:, 1], hue=pred_new*-1,
                s=100, alpha=0.7, palette=['tab:blue', 'tab:red'],
                ec='orange', legend=None, ax=ax)
# 未知データのデータ番号を付記
for i, ((x_pos, y_pos), label) in enumerate(zip(data_new_ss, pred_new)):
       color = str(np.where(label == 1, 'tab:blue', 'tab:red'))
       ax.annotate(text=i+1, xy=[x_pos-0.2, y_pos+0.2], color=color, fontsize=14)
# 凡例
ax.plot([], [], color='tomato', lw=1, ls='--', label='決定境界')
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles=handles, labels=['正常', '異常', '閾値'], title='異常検知')
# 修飾
ax.set(xlabel='total_phenols', ylabel='Color intensity',
       title='One-Class SVMによる異常検知')
ax.grid(lw=0.5);

【実行結果】
大きな赤い点の３つのデータが異常度の閾値を超えている様子が分かります。
データ番号を付記しています。

続いてスコアを用いて管理図ライクな図を描画します。

### 異常判別の描画

# 描画領域の指定
fig, ax = plt.subplots(figsize=(10, 5))
# 正常値の散布図の描画
query1 = pred_new >= 0
sns.scatterplot(x=np.where(query1)[0] + 1, y=score_samples_new[query1], s=80,
                color='lightblue', ec='tab:blue', ax=ax, label='正常値')
# 異常値の散布図の描画
query2 = pred_new < 0
sns.scatterplot(x=np.where(query2)[0] + 1, y=score_samples_new[query2], s=80,
                color='lightpink', ec='tab:red', ax=ax, label='異常値')
# 閾値の水平線の描画
ax.axhline(clf.offset_, color='tomato', ls='--', label='閾値')
# 修飾
ax.set_title(f'One-Class SVM  異常度の閾値 {clf.offset_[0]:.2f}')
ax.set(xlabel='データ番号', ylabel='異常度（スコア）', ylim=(0.8, 1.6))
ax.grid(lw=0.5)
ax.legend(loc='lower left');

【実行結果】
４番目のデータは正常値にかなり近いです。
異常検知の閾値作りはある程度の困難（または割り切り）が要求される感じがいたしました。

One-Class SVM による異常検知は以上です。

品種ごとの色分け

テキストの配布コードで紹介されている「品種ごとの色分け」（テキスト148ページ）の図を描画してみます。
品種ラベルはデータセット読み込みの際に「target」に設定しました。

### classごとに色を分けたMagnesiumとColor_intensityの散布図の描画
plt.figure(figsize=(5, 5))
sns.scatterplot(x=df['magnesium'], y=df['color_intensity'], hue=target['class'],
                palette=['lightblue', 'lightpink', 'lightgreen'], ec='honeydew',
                s=80)
plt.grid(lw=0.5);

【実行結果】
テキストの Flavonoids ＋ Color Intensity と比べると混ざり気味ですが、ざっくり３種の塊は見られるようです。

ホテリングのT²法

テキスト7-1-3節「補足」の「ホテリングの$${T^2}$$法」による異常検知に関連して描画される「図7-10」相当を描画します
学習データを用いて学習を行い、ユークリッド距離とマハラノビス距離の等高線図を描画します。

■ 学習
データ点の「平均」とデータ間の「分散共分散行列の逆行列」を算出します。

### ホテリングのT²法のパラメータ＝マハラノビス距離のパラメータの算出
# 2変数x,yの変数ごとの平均値
means = data.mean(axis=0)
# 2変数x,yの分散共分散行列の逆行列
cov_i = np.linalg.pinv(data.cov())

■ 描画
等高線データの作成コードはテキストの配布コードをお借りいたします。

### 等高線描画用データの作成

# 平均からのユークリッド距離（同心円）
z1 = np.array([[(i, j, distance.euclidean([i, j], means))
                for i in np.linspace(-4, 5, 100)]
                for j in np.linspace(-4, 5, 100)])

# 平均からのマハラノビス距離（楕円）
z2 = np.array([[(i, j, distance.mahalanobis([i, j], means, cov_i))
                for i in np.linspace(-4, 5, 100)]
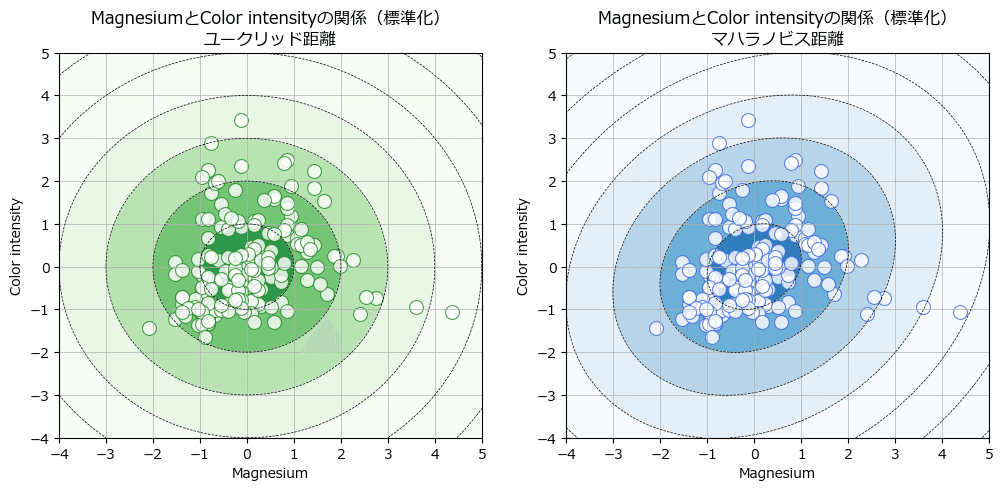
                for j in np.linspace(-4, 5, 100)])

等高線を描画します。
テキストの配布コードの構成をお借りしています。

### 2変数のユークリッド距離（同心円）、マハラノビス距離（楕円）の可視化

## 描画領域の指定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

## 左のユークリッド距離の描画
# ユークリッド距離の等高線・等高面の描画
ax1.contour(z1.T[0], z1.T[1], z1.T[2], colors=['black'], linestyles='--',
            linewidths=0.5)
ax1.contourf(z1.T[0], z1.T[1], z1.T[2], vmin=-1, vmax=4, cmap='Greens_r')
# 散布図の描画
sns.scatterplot(data=data, x='x', y='y', color='white', ec='forestgreen',
                alpha=0.8, s=100, ax=ax1)
# 修飾
ax1.set(xlabel='Magnesium', ylabel='Color intensity',
        title='MagnesiumとColor intensityの関係（標準化）\nユークリッド距離')
ax1.grid(lw=0.5)

## 右のマハラノビス距離の描画
# マハラノビス距離の等高線・等高面の描画
ax2.contour(z2.T[0], z2.T[1], z2.T[2], colors=['black'], linestyles='--',
            linewidths=0.5)
ax2.contourf(z2.T[0], z2.T[1], z2.T[2], vmin=-1, vmax=4, cmap='Blues_r')
# 散布図の描画
sns.scatterplot(data=data, x='x', y='y', color='white', ec='royalblue',
                alpha=0.8, s=100, ax=ax2)
# 修飾
ax2.set(xlabel='Magnesium', ylabel='Color intensity',
        title='MagnesiumとColor intensityの関係（標準化）\nマハラノビス距離')
ax2.grid(lw=0.5);

【実行結果】
両方の等高線の形状はデータのＬ字型分布を捉えきれていません。
適材適所で異常検知手法を選択することが大切かもですね。

第７章②の寄り道写経は以上です。

---

シリーズの記事

次の記事

前の記事

目次

ブログの紹介

---

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは Ｒ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経 ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。