
7-5 非正規母集団に対する母平均の信頼区間 ~ 所得分布が近似する確率分布を探せ!(PythonのFitter)
今回の統計トピック
母集団が正規分布に従っていないときの母平均の信頼区間について深掘りします。
後半では、政府統計データを用いて「所得の分布」をグラフにしたり、信頼区間を求めたり、Pythonの「Fitter」で所得分布が従う確率分布に迫ります!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
知る+問題を解く
📘公式問題集のカテゴリ
推定の分野
問5 非正規母集団に対する母平均の信頼区間(全国世帯の年間所得金額)
試験実施年月
統計検定2級 2019年11月 問14(回答番号24)
問題
公式問題集をご参照ください。
題意
母集団が正規分布に従っていないと考えられる場合の母平均の信頼区間について、次の統計量$${Z}$$に関わらせて、5つの選択肢の中から適切なものを1つ選びます。
・統計量$${Z=\cfrac{\bar{X}-\mu}{\sqrt{S^2/n}}}$$
・標本平均$${\bar{X}}$$
・母平均$${\mu}$$
・不偏分散$${S^2}$$
・標本サイズ$${n}$$
今回の記事の構成
この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」と「知る」の章を1つの章にまとめます。
最初は「知る」のゾーンです。
母平均の信頼区間の概要を学びます。
その後「問題を解く」のゾーンに移ります。
母平均の信頼区間
📕公式テキスト:3.4.1 正規分布の母平均の推定(114ページ)、
3.4.2 母分散が未知の場合の母平均の推定:$${t}$$分布の利用(114ページ~)
■母平均の信頼区間の計算パターン
最初に統計検定2級の公式テキストに掲載された「母平均の信頼区間の計算パターン3つ」を確認いたします。
文中に用いる記号は、前述の題意のものに加えて、次の記号を用います。
$${\sigma^2}$$:母分散
$${z_{\alpha/2}}$$:標準正規分布の上側確率$${\alpha/2}$$パーセント点
$${t_{\alpha/2}(n-1)}$$:自由度$${n-1}$$の$${t}$$分布の上側確率$${\alpha/2}$$パーセント点
パターン1:母分散$${\boldsymbol{\sigma^2}}$$が既知の場合
【条件】
・標本が独立に正規分布$${N(\mu, \sigma^2)}$$に従うこと
・母分散$${\sigma^2}$$の値が分かっていること
【利用する確率変数と確率分布】
・確率変数$${Z}$$が標準正規分布に従うことを利用します。
$$
Z=\cfrac{\bar{X}-\mu}{\sqrt{\sigma^2/n}} \sim N(0,1)
$$
【母平均の信頼区間の公式1】
「母分散$${\sigma^2}$$」と「標準正規分布の上側確率$${\alpha/2}$$パーセント点$${z_{\alpha/2}}$$」を利用します。
$$
\bar{X} - z_{\alpha/2}\sqrt{\cfrac{\sigma^2}{n}} \leq \mu \leq \bar{X} + z_{\alpha/2}\sqrt{\cfrac{\sigma^2}{n}}
$$
パターン2:母分散$${\boldsymbol{\sigma^2}}$$が未知で標本サイズ$${\boldsymbol{n}}$$が大きい場合
【条件】
・標本が独立に正規分布$${N(\mu, \sigma^2)}$$に従うこと
・母分散$${\sigma^2}$$の値が分かっていないこと
・標本サイズ$${n}$$が大きいこと(公式テキストは$${n>100}$$を例示)
【利用する確率変数と確率分布】
・確率変数$${Z'}$$が標準正規分布に「近似的に」従うことを利用します。
$$
Z'=\cfrac{\bar{X}-\mu}{\sqrt{S^2/n}} \simeq N(0,1)
$$
【母平均の信頼区間の公式2】
母分散の代わりに「(標本)不偏分散$${S^2}$$」を用いて、「標準正規分布の上側確率$${\alpha/2}$$パーセント点$${z_{\alpha/2}}$$」を利用します。
$$
\bar{X} - z_{\alpha/2}\sqrt{\cfrac{S^2}{n}} \leq \mu \leq \bar{X} + z_{\alpha/2}\sqrt{\cfrac{S^2}{n}}
$$
(注)$${\sqrt{\cfrac{S^2}{n}}}$$は標準誤差です。
パターン3:母分散$${\boldsymbol{\sigma^2}}$$が未知で標本サイズ$${\boldsymbol{n}}$$が大きくない場合
【条件】
・標本が独立に正規分布$${N(\mu, \sigma^2)}$$に従うこと
・母分散$${\sigma^2}$$が分かっていないこと
・標本サイズ$${n}$$が大きくないこと
【利用する確率変数と確率分布】
・確率変数$${t}$$が自由度$${n-1}$$の$${t}$$分布に従うことを利用します。
$$
t=\cfrac{\bar{X}-\mu}{\sqrt{S^2/n}} \sim t(n-1)
$$
【母平均の信頼区間の公式3】
「(標本)不偏分散$${S^2}$$」と「自由度$${n-1}$$の$${t}$$分布の上側確率$${\alpha/2}$$パーセント点$${t_{\alpha/2}(n-1)}$$」を利用します。
$$
\bar{X} - t_{\alpha/2}(n-1)\sqrt{\cfrac{S^2}{n}} \leq \mu \leq \bar{X} + t_{\alpha/2}(n-1)\sqrt{\cfrac{S^2}{n}}
$$
(注)$${\sqrt{\cfrac{S^2}{n}}}$$は標準誤差です。
まとめ1
3つのパターンは「標本が独立に正規分布に従っていること」を条件にしています。
■標本が独立に正規分布に従うケース
次に、統計検定2級の公式テキストに掲載された「標本が正規分布に独立に従うケース2つ」を確認しましょう。
ケース①母集団が正規分布
【条件】
・母集団が正規分布に従っていること
・母集団から無作為抽出しているなど、標本が互いに独立であること
ケース②標本サイズ$${\boldsymbol{n}}$$が大きい
【条件】
・標本サイズ$${n}$$が大きいこと
・母集団から無作為抽出しているなど、標本が互いに独立であること
(母集団が正規分布に従っていなくてもOKです)
【理由】
標本サイズ$${n}$$が大きくなると、母集団が正規分布でない場合でも、中心極限定理により、$${Z=\cfrac{\bar{X}-\mu}{\sqrt{S^2/n}}}$$は標準正規分布に近似的に従います。
まとめ2
母集団が正規分布に従っていない場合、標本サイズ$${n}$$が大きいときに$${Z}$$は標準正規分布に従います。
問題を解く
問題に戻ります。
条件に合致する選択肢の検討
標本は母集団から無作為抽出されているので、標本は互いに独立です。
そして、母集団が正規分布に従っていないと考えられるので、統計量$${Z=\cfrac{\bar{X}-\mu}{\sqrt{S^2/n}}}$$が正規分布に従う条件は、標本サイズ$${n}$$が十分大きいときです。
このとき、$${Z}$$は近似的に標準正規分布に従います(パターン2)。
選択肢の中で「標本の大きさが十分大きい場合に、$${Z}$$は標準正規分布に近似的に従う」ことを述べているのは、選択肢3です。
正解は選択肢3です。
その他の選択肢の確認
その他の選択肢について確認します。
選択肢4
「母集団の分布と標本の大きさにかかわらず、$${Z}$$は標準正規分布に従う」
統計量$${Z=\cfrac{\bar{X}-\mu}{\sqrt{S^2/n}}}$$は標本の大きさが大きい場合に標準正規分布に近似的に従う(パターン2)ので、この記述は誤りです。
選択肢2
「母集団の分布と標本の大きさにかかわらず、$${Z}$$は自由度$${n-1}$$の$${t}$$分布に従う」
統計量$${Z=\cfrac{\bar{X}-\mu}{\sqrt{S^2/n}}}$$が自由度$${n-1}$$の$${t}$$分布に従うのは、「標本が正規分布に従う」とき、または、「母集団の分布から自由度$${n-1}$$の$${t}$$分布に従う」ことが明確なときです。
「母集団の分布と標本の大きさにかかわらず」という条件の部分が適切ではありません。
選択肢1
「母集団の分布と標本の大きさにかかわらず、$${Z}$$は自由度1のカイ二乗分布に従う」
統計量$${Z=\cfrac{\bar{X}-\mu}{\sqrt{S^2/n}}}$$が自由度1のカイ二乗分布に従うかどうかは「母集団の分布次第」と思われます。
「母集団の分布と標本の大きさにかかわらず」という条件の部分が適切ではありません。
選択肢5
「標本の大きさが十分小さい場合に、$${Z}$$は二項分布に近似的に従う」
統計量$${Z=\cfrac{\bar{X}-\mu}{\sqrt{S^2/n}}}$$が二項分布に従うかどうかは「母集団の分布次第」と思われます。
「標本の大きさが十分小さい場合」という条件の部分が適切ではありません。
解答
③ です。
難易度 やさしい
・知識:母平均の信頼区間
・計算力:不要
・時間目安:1分
実践する
おしながき
公式問題集の問題に接近してみましょう!
今回は「2021年の各種世帯の所得等の状況に関するデータ」を利用して、所得の分布を可視化と、平均所得の信頼区間を計算を実施しましょう。
また、公式問題集掲載の2016年の分布と期間比較してみましょう。
そして、2021年の所得分布に近似する確率分布をPythonで探し当てましょう。
我が国の所得の分布に切り込んでいきます!!!
【出典記載】
出典:「令和3年国民生活基礎調査」(厚生労働省)
【コンテンツ編集・加工の記載】
記事の記載にあたっては、「令和3年国民生活基礎調査」(厚生労働省)を加工して作成しています。
データを取得する
政府の統計サイト
「各種世帯の所得等の状況に関するデータ」は政府統計の総合窓口「e-Stat」で公開されています。
厚生労働省の「国民生活基礎調査」による統計データを利用します。
2021年(令和3年)の国民生活基礎調査(所得・年次)のデータセットは、次のページの一覧から利用するデータを選択して、取得します。
「世帯数の相対度数分布-累積度数分布,年次・所得金額階級別」データはこちらのページより、CSVまたはDBを選択して、データを表示・ダウンロードします。

2021年(令和3年)の国民生活基礎調査の概況については、厚生労働省のWebサイトでも公開されています。
利用データの取得元
今回利用するデータの取得元をまとめます。
資料①:調査世帯数(集計客体数:5142)
厚生労働省Webサイトより
【ダウンロード】
https://www.mhlw.go.jp/toukei/saikin/hw/k-tyosa/k-tyosa21/dl/01.pdf
【資料の利用箇所(抜粋)】

資料②:所得金額階級別世帯数の相対度数分布
厚生労働省Webサイトより
【ダウンロード】
https://www.mhlw.go.jp/toukei/saikin/hw/k-tyosa/k-tyosa21/dl/03.pdf
政府統計サイトe-Stat掲載の階級と比べて、1000万円~2000万円の階級の粒度が細かいので、こちらの資料の相対度数を使います。
【資料の利用箇所(抜粋)】

資料③:1世帯当たり平均所得金額の推計値と標準誤差
厚生労働省Webサイトより
【ダウンロード】
https://www.mhlw.go.jp/toukei/list/dl/20-21-gosa_r3.pdf
平均所得金額の信頼区間の計算に当たり、標準誤差の金額は厚生労働省公表データを活用します。
標本不偏分散$${S^2}$$を算出するデータが無いためです。
【資料の利用箇所(抜粋)】

ちなみに、厚生労働省の資料では、次のように 95% 信頼区間の計算に触れています(赤下線は筆者による)。

■CSVファイルのダウンロード
こちらのリンクから整形後のCSVファイルをダウンロードできます。
CSVデータの内容です。資料③と公式問題集のデータを引用しています。

電卓・手作業で作成してみよう!
まず、階級の幅が100万円の所得金額階級別世帯数の相対度数分布表をざっと見ておきましょう。
2021年の方が、所得金額の高い階級の割合が増えている感じがします。

(1)2021年のヒストグラムをプロットする
相対度数分布表のデータから2021年のヒストグラムを作ってみましょう。
横軸に階級、縦軸に2021年の相対度数をプロットします。
次のグラフは作成例です。

ヒストグラムの形状を見てみましょう。
正規分布のような左右対称の形状になっていません。
「所得金額は母集団が正規分布に従っていない」ということが可視化することでよくわかります。
ヒストグラムの形状をもう少し詳しく見てみましょう。
右に裾が長く伸びています。
右に裾が長い分布なので、おそらく「歪度は正の値」でしょう。
歪度については記事「5-6 分布形と歪度・尖度」で詳しく取り扱っています。
中央値と平均値を追記する
次のヒストグラムには中央値と平均値を追記しました。

中央値はデータ数の 50% の地点です。
1000万円の位置を図の中心として見るとき、中央値(440万円)は約 20% の位置になります。
中央値はずいぶん左側(所得金額の小さい側)に寄っており、高所得層がロングテールのように右側に長い裾をもたらしています。
ジニ係数はおそらく格差の存在を示す値になるでしょう。
記事「1-8 ローレンツ曲線・ジニ係数の説明」で詳しく取り扱っています。
(2)95% 信頼区間を計算する
平均所得金額の 95% 信頼区間を計算します。
①標本サイズ
資料①より標本サイズ$${n=5142}$$です。
標本サイズが大きいので標準正規分布に近似的に従うものとして扱います。
つまり「パターン2」です。
②標本平均と標準誤差
資料③より、標本平均(平均所得金額)は 564.3万円、標準誤差は 10.3万円です。
利用する統計データは既にさまざまな統計処理を実施済みであり、統計処理の過程で計算された標準誤差を利用するのがよいと思いました。
③標準正規分布の上側確率 2.5%点
95%信頼区間の場合、標準正規分布の上側確率2.5%点$${z_{0.025}}$$を取得します。
標準正規分布の上側確率表を見ましょう。
上側確率2.5%点$${z_{0.025}=1.96}$$です。

④ 95% 信頼区間を計算する
次の値をパターン2の信頼区間の公式に当てはめます。
標本平均$${\bar{X}=564.3}$$万円
標準正規分布の上側確率2.5%点$${z_{\alpha/2}=z_{0.025}=1.96}$$
標準誤差の推定値$${\sqrt{\cfrac{S^2}{n}}=10.3}$$万円
【計算】
$$
\begin{align*}
\bar{X} - z_{\alpha/2}\sqrt{\cfrac{S^2}{n}} \leq &\mu \leq \bar{X} + z_{\alpha/2}\sqrt{\cfrac{S^2}{n}} \\
\\
564.3万円 \times (-1.96)\times 10.3万円 \leq &\mu \leq 564.3万円 \times 1.96 \times 10.3万円 \\
\\
544.1万円 \leq &\mu \leq 584.5万円
\end{align*}
$$
計算完了です!
【解答】
2021年の平均所得金額の95%信頼区間は、$${[544.1万円, 584.5万円]}$$、または、$${564.3万円 \pm 20.2万円}$$です。
(3)2016年と2021年の2期データを比べる
相対度数分布表の数値を用いて、2016年と2021年の相対度数を比較するグラフを描いてみましょう。
①棒グラフ
まずは、棒グラフで2期分を並べてみましょう。

大きな変動は無さそうです。
300万円未満は2016年の方が割合が大きいです。
一方で300万円以上は2021年の方が概ね割合が大きいです。
2021年の方が所得金額の大きい世帯の割合が大きくなった感じです。
②100%積み上げ横棒グラフ
相対度数分布の場合、合計は100%(実際は端数処理により上下する)になります。
所得金額階級の割合を比較するには、100%積み上げ横棒グラフが適していると思います。

積み上げ80%付近のプロットを見てみましょう。
2016年は、800万円以上の所得は80%以上のエリアになっています。
上位20%が800万円以上です。
一方で2021年は、800万円以上は約78%以上になっています。
上位22%が800万円以上です。
やはり、2021年の方が所得金額の大きい世帯の割合が大きくなった感じがします。
【希望】
物価上昇期に突入しています。
物価上昇以上に所得金額が増加することを希望いたします!
③散布図
2016年と2021年の相対度数を散布図にプロットしました。
2期の各所得金額階級の割合には大きな相関があるようです。

EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。
グラフの紹介
この記事で利用したグラフはEXCELで作成しました。

集合縦棒グラフを作成する
グラフを1つ作成してみましょう。
ここでは「②の集合縦棒グラフ」を取り上げて、作成手順を明らかにします!
最初のステップはグラフにしたいデータ範囲を選択して、グラフを選ぶところまでです。

①データを選択
グラフにする2016年と2021年の相対度数データを範囲指定します。
このとき、見出しの「2016年」「2021年」も範囲に含めます。
②挿入を選択
メニューから「挿入」を選びます。
③「グラフ」の斜め矢印を選択
「挿入」メニューの「グラフ」部分の右すみっこに小さな矢印あります。
この部分をクリックします。
「グラフの挿入」画面が出現します。
④集合縦棒を選択
「グラフの挿入」画面の「おすすめグラフ」(または「すべてのグラフ」>「縦棒」)に表示されるグラフサンプルの中から作成したいグラフを選択します。
⑤OKを選択
「グラフの挿入」画面の「OK」ボタンをクリックします。
次のステップはグラフの整形です。
グラフの横軸ラベルに「階級」を表示しましょう。

⑥データの選択を選択
グラフの余白を右クリックすると図のメニューが出現します。
「データの選択」をクリックします。
「データソースの選択」画面が出現します。
⑦編集を選択
「データソースの選択」画面の右側のゾーンに横軸ラベルを指定します。
まず「編集」ボタンをクリックします。
「軸ラベル」画面が出現します。

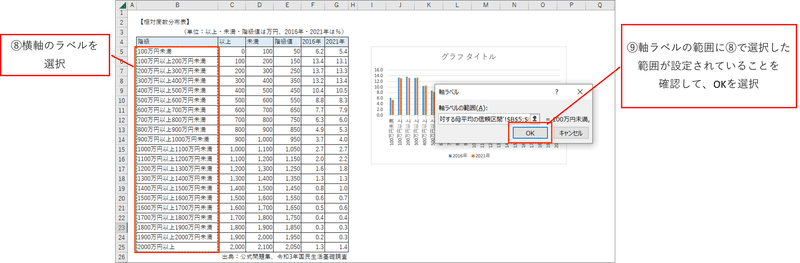
⑧横軸のラベルを選択
「軸ラベル」画面の入力エリアにカーソルがあることを確認して、相対度数分布表の「階級」列を範囲指定します。
見出し「階級」は含めません。
⑨軸ラベルの範囲に⑧で選択した範囲が設定されていることを確認して、OKを選択
「軸ラベル」画面の入力エリアに、度数分布表の B5:B25 が入っていることを確認して、「OK」ボタンをクリックします。
「データソースの選択」画面に戻ります。

⑩横(項目)軸ラベルの欄に表示されたテキストが適切かどうかを確認して、OKを選択
「横(項目)軸ラベル」欄に階級(100万円未満など)が表示されました。
「OK」ボタンをクリックします。
最後に、横軸のラベルの見栄えを整えましょう。
⑩の完了時には次のように横軸の階級の文字が縦になったり、文章が途切れてしまっています。

これを整える方法の1つがこれです。
「グラフを縦・横に広げる」
グラフの端をドラッグして縦横に伸ばした結果が次の画像です。
横軸の階級の文字が斜めに回転して読みやすくなりました。
また、文章の途切れも無くなりました。

以上です!
近似曲線を描いてみる
次のグラフを見てみましょう。
棒グラフの頂点に沿って曲線が描かれています。

EXCELの近似曲線の機能を使いました。
右上に2021年の近似曲線の数式と決定係数$${R^2}$$を併記しました。
6次関数です。機械学習の世界では「過学習」と言われるレベルかもです!
近似曲線を追加しましょう。

①グラフをクリックすると右側に+のボタンが表示されます。
+をクリックします。
「グラフ要素」のメニューが出現します。
②「グラフ要素」メニューの「近似曲線」の右の>をクリックします。
③「その他オプション」をクリックします。
「近似曲線の追加」画面が出現します。
④「近似曲線の追加」画面で近似曲線作成対象のデータを指定します。
ここでは、2021年を選択します。
⑤「OK」ボタンをクリックします。
画面右に「近似曲線の書式設定」メニューが出現します。

⑥グラフアイコンをクリックします。
⑦「近似曲線のオプション」ゾーンにて、使いたい近似を指定します。
ここでは「多項式近似」とし、「次数」に6を設定します。
6次関数で近似する、こんなイメージです。
⑧近似曲線の数式と決定係数$${R^2}$$を表示する場合には、次の2項目にチェックを入れます。
「グラフに数式を表示する」
「グラフにR-2乗値を表示する」
所得分布のグラフから6次の近似曲線を推定しました。
この近似曲線(6次関数)を参考にして、他の年の所得分布を推定することは、アバウトな意味ではアリだと思います。
しかし、もう少しシンプルな確率分布の関数を見いだせないでしょうか・・・。
こんな声に対応します!
Pythonの「Fitter」を使って、2021年の所得分布が近似する確率分布を探しに行きましょう!
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
2021年の所得分布が近似的に従う確率分布を見つけましょう。
Pythonのコードを紹介しながら、当てはまりの良い確率分布に迫ります!
Fitterの紹介
Fitterはデータに適合(FIT)する確率分布とパラメータを探索するPythonのパッケージです。
SciPyに用意された確率分布を対象にして探索するそうです。
Fitterのサイトはこちら!
①インポート
3行目がFitterです。
import numpy as np
import pandas as pd
from fitter import Fitter
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline②相対度数分布表データフレームの作成
2016年と2021年の所得金額階級別世帯数の相対度数分布表のデータフレームを作成します。
階級の幅は100万円です(ただし、2000万円以上を除く)。
### 列の値の設定
# 階級
class_label = ['100万円未満', '100万円以上200万円未満', '200万円以上300万円未満',
'300万円以上400万円未満', '400万円以上500万円未満',
'500万円以上600万円未満', '600万円以上700万円未満',
'700万円以上800万円未満', '800万円以上900万円未満',
'900万円以上1000万円未満', '1000万円以上1100万円未満',
'1100万円以上1200万円未満', '1200万円以上1300万円未満',
'1300万円以上1400万円未満', '1400万円以上1500万円未満',
'1500万円以上1600万円未満', '1600万円以上1700万円未満',
'1700万円以上1800万円未満', '1800万円以上1900万円未満',
'1900万円以上2000万円未満', '2000万円以上']
# 階級(以上)
class_low = [i for i in range(0, 2001, 100)]
# 階級(未満)
class_high = [i for i in range(100, 2101, 100)]
# 階級値
class_value = [i for i in range(50, 2051, 100)]
# 2016年相対度数
freq_value_2021 = [5.4,13.1,13.3,13.4,10.5,8.3,7.9,6.0,5.3,4.0,
2.7,2.2,1.8,1.3,1.0,0.7,0.6,0.4,0.3,0.3,1.4]
# 2021年相対度数
freq_value_2016 = [6.2,13.4,13.7,13.2,10.4,8.8,7.7,6.3,4.9,3.7,
2.7,2.0,1.6,1.3,0.8,0.6,0.5,0.4,0.3,0.2,1.3]
### データフレームの作成
df = pd.DataFrame({'階級': class_label,
'階級(以上)': class_low,
'階級(未満)': class_high,
'階級値': class_value,
'2021年相対度数': freq_value_2021,
'2016年相対度数': freq_value_2016})
### データフレームの表示
display(df)相対度数分布表が出来上がりました。
2000万円以上の階級は上限が定かではないため、2000万円以上2100万円以下の幅を仮置きしています。
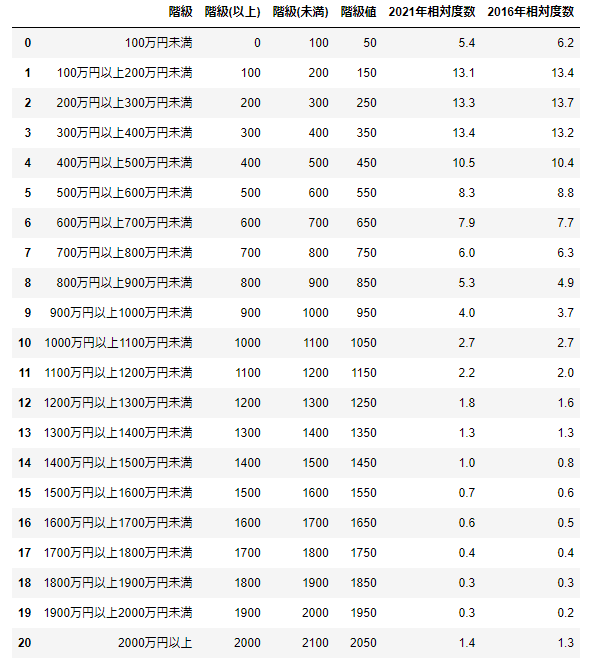
③所得rawデータの作成
2021年の相対度数分布表データをFitterで取り扱える形式に整えます。
具体的には、NumPyのrepeatで度数分のデータを生成します。
例えば、100万円未満の階級データは、階級値「50」のデータを相対度数×10に相当する「54個」作成します。
また、階級「2000万円以上」は除外します。
範囲(いくらまで)が不定のためです。
# データフレームの作成
df_dist_fitter = pd.DataFrame({'data': np.repeat(df.iloc[0:-1, 3],
df.iloc[0:-1, 4]*10)})
# データフレームの概要を表示
print('所得rawデータの形状: ', df_dist_fitter.shape)
display(df_dist_fitter.head())
print('所得rawデータの要素の個数をカウント:\n',
df_dist_fitter.value_counts(sort=False))
985行1列のデータが出来ました。
「所得rawデータの要素の個数をカウント」をご覧ください。
階級値と度数(相対度数×10)は2021年の相対度数分布表と同じになっていることが確認できます。
この「所得rawデータ」のヒストグラムも確認しましょう。
④所得rawデータのヒストグラムをプロット
bins = [i for i in range(50, 2100, 100)]
plt.hist(df_dist_fitter['data'], bins=bins);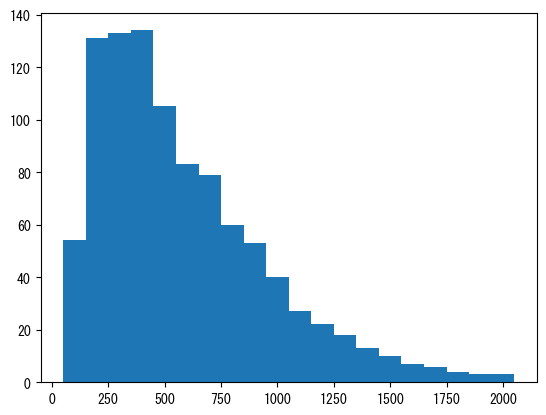
EXCELのグラフと同じ形状になっていることを確認しましょう。
(こちらのほうが少し縦長です)
準備が整いましたので、所得rawデータが近似的に従う確率分布を探索しましょう!
⑤所得rawデータが従う確率分布を探索する
SciPyが取り扱う100以上の確率分布のうち、メジャーな15個を対象にして探索します。
探索対象の確率分布は「dist」(リスト)に設定した正規分布からレイリー分布までです。
### Fitterで確率分布を探索
# 設定:探索対象の確率分布を指定
dist = ['norm', # 正規分布
'lognorm', # 対数正規分布
'chi2', # カイ二乗分布
't', # t分布
'f', # F分布
'expon', # 指数分布
'uniform', # 一様分布
'beta', # ベータ分布
'gamma', # ガンマ分布
'loggamma', # 対数ガンマ分布
'cauchy', # コーシー分布
'pareto', # パレート奉納
'weibull_min', # ワイブル分布
'weibull_max', # ワイブル分布
'rayleigh'] # レイリー分布
# 所得rawデータを探索対象の確率分布をfit
f = Fitter(df_dist_fitter.iloc[:, 0].values.tolist(), distributions=dist, bins=20)
f.fit()
# 適合状況とヒストグラムを表示
f.summary()【コードの解説】
Fitterのコードは簡潔です。
まず、f=Fitter()でインスタンスを生成しています。
今回利用した引数は次の3つです。
・データ(PandasのSeriesの取り扱いに難儀しました・・・)
・distributions : 探索対象の確率分布
・bins : 階級の数
次に、f.fit()で確率分布の適合を探索します。
最後のf.summary()で探索結果を表示します。
f.fit()の実行中は、プログレスバーが表示され、進捗状況を把握できます。

適合(fit)の処理が終わるとf.summary()による結果を表示してくれます。

表は適合度の高い順に5つの確率分布を表示しています。
適合度の評価指標は「残差二乗和」(sum of squared residuals)です。
最も適合したのは「ガンマ分布」です。
グラフを見てみましょう。
所得rawデータのヒストグラム(相対度数)と5つの分布の曲線が表示されます。

ガンマ分布(gamma)と$${F}$$分布(f)が重なったため、ガンマ分布のグラフが見えないです・・・。
「ガンマ分布は$${F}$$分布(f)の曲線と同じ」という風に見てください!
ベストフィットのガンマ分布のパラメータを確認しましょう。
⑥ベストの確率分布のパラメータを確認する
f.get_best()
f.get_best()で取得できます。シンプルなコードですね!
ガンマ分布の3つのパラメータ値がわかりました。
総まとめとして改めて、相対度数分布表データのヒストグラムと上記パラメータのガンマ分布の曲線を重ねて可視化しましょう。
今度は2000万円以上の階級を表示します。
⑦所得金額階級別世帯数の相対度数とガンマ分布を重ねてプロット
# インポート:ガンマ分布
from scipy.stats import gamma
# ガンマ分布のパラメータを取得
a, loc, scale = f.get_best()['gamma'].values()
# ガンマ分布の確率も都度関数の値を取得
x = np.linspace(0, 2000, 10001)
y = gamma.pdf(x, a=a, loc=loc, scale=scale)
# 相対度数データのプロット
plt.bar(df['階級値'], df['2021年相対度数']/10000, label='所得金額階級別世帯数', width=95)
# ガンマ分布のプロット
plt.plot(x, y, label='ガンマ分布', color='red')
plt.legend()
plt.show()2021年の所得金額階級別世帯数のヒストグラム、および、近似するガンマ分布の確率密度関数のグラフです。

ガンマ分布がいい感じにフィットしていることを確認できました。
「2021年の所得分布はガンマ分布に近似するようだ」
結論はこんな感じにしておきましょう。
所得分布に関する研究
ちなみにネット検索によると、学術の分野では長年、所得分布が従う確率分布を追求しているような印象を得ました。
例えば次のpdfは、九州大学のリポジトリに保管された1987年の論文「所得分布に関する分布関数の推定」です。
ガンマ分布にも触れています(所得分布はガンマ分布に従う、とは書いていません)。
https://catalog.lib.kyushu-u.ac.jp/opac_download_md/4486576/530102_p197.pdf
中長期にわたる経済的な成長と経済政策・所得再分配などの取り組みによって所得分布が構成されるような気がします。
ある一時点の分布が将来にわたって継続するかどうかは、未知の世界です。
ところで、ガンマ分布って何でしょう?
ガンマ分布
ガンマ分布は指数分布を一般化した分布です。
ガンマ分布に従う事象の例は、人の体重、ウイルスの潜伏期間、電子部品の寿命など、だそうです。
「統計WEB」さんの情報をお借りしました。ありがとうございます!
ガンマ分布の確率密度関数
難しい数式がたくさん出てきました。。。
【定義1】
$$
f(x, \alpha, \beta)=\cfrac{\beta^{\alpha} x^{\alpha-1} e^{-\beta x}}{\Gamma(\alpha)} \quad (x \geq 0)
$$
または
【定義2】
$$
f(x, \alpha, \beta)=\cfrac{ x^{\alpha-1} e^{-\frac{x}{\beta}} }{\beta^{\alpha}\Gamma(\alpha)} \quad (x \geq 0)
$$
ガンマ分布$${Ga(\alpha, \beta)}$$のパラメータは$${\alpha}$$と$${\beta}$$($${\alpha, \beta > 0}$$)です。
$${\alpha}$$は形状母数、$${\beta}$$は尺度母数と呼ばれています。
$${\Gamma}$$はガンマ関数と呼ばれる数式です。
SciPyのガンマ分布の確率密度関数(定義1)のパラメータは次の3つです。
・a : パラメータ$${\alpha}$$
・scale : パラメータ$${\beta}$$
・loc : x軸の位置
ガンマ分布の形状
Pythonでさまざまなパラメータ値のガンマ分布を確認しましょう。
⑧ガンマ分布の確率密度関数の描画
パラメータ$${\alpha}$$を動かしてみましょう。
alpha_listのパラメータにさまざまな値を設定して、ガンマ分布の形状の変容を試してみてくださいね!
### パラメータα
alpha_list = [1, 2, 5, 10]
# その他のパラメータ
beta, loc = 1, 0
# 描画
x = np.linspace(0, 20, 10001)
for alpha in alpha_list:
y = gamma.pdf(x, a=alpha, loc=loc, scale=beta)
plt.plot(x, y, label=f'$\\alpha={alpha},\ \\beta={beta},\ loc={loc}$')
plt.legend()
plt.title(r'ガンマ分布:パラメータ$\alpha$を変える')
plt.show()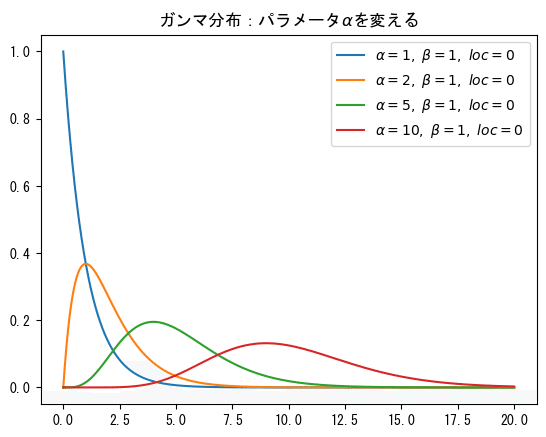
$${\alpha}$$の値が大きくなるにつれて、峰のピークが右側に移動して低くなっています。
次にパラメータ$${\beta=scale}$$を動かしてみましょう。
beta_listのパラメータにさまざまな値を設定して、ガンマ分布の形状の変容を試してみてくださいね!
### パラメータβ
beta_list = [1, 1.5, 2, 3]
# その他のパラメータ
alpha, loc = 2, 0
# 描画
x = np.linspace(0, 20, 10001)
for beta in beta_list:
y = gamma.pdf(x, a=alpha, loc=loc, scale=beta)
plt.plot(x, y, label=f'$\\alpha={alpha},\ \\beta={beta},\ loc={loc}$')
plt.legend()
plt.title(r'ガンマ分布:パラメータ$\beta$を変える')
plt.show()
$${\beta}$$の値が大きくなるにつれて、峰のピークが右側に移動して低くなっています。
最後に パラメータ$${loc}$$を動かしてみましょう。
loc_listのパラメータにさまざまな値を設定して、ガンマ分布の形状の変容を試してみてくださいね!
### パラメータloc
loc_list = [0, 1, 2, 5]
# その他のパラメータ
alpha, beta = 2, 2
# 描画
x = np.linspace(0, 20, 10001)
for loc in loc_list:
y = gamma.pdf(x, a=alpha, loc=loc, scale=beta)
plt.plot(x, y, label=f'$\\alpha={alpha},\ \\beta={beta},\ loc={loc}$')
plt.legend()
plt.title(r'ガンマ分布:パラメータ$loc$を変える')
plt.show()
パラメータ$${loc}$$の値に従って、グラフが右に移動します。
もう一度、2021年の所得に近似するベストなパラメータ値のガンマ分布をおさらいしましょう。
【パラメータ値】
$${\alpha=1.5685774919271473}$$
$${\beta=scale=319.8214254058897}$$
$${loc=28.43681200917777}$$
# ベストなパラメータ値
alpha = 1.5685774919271473
beta = 319.8214254058897
loc = 28.43681200917777
# 描画
x = np.linspace(0, 2000, 10001)
y = gamma.pdf(x, a=alpha, loc=loc, scale=beta)
plt.plot(x, y, label=f'$\\alpha={alpha:.3f},\ \\beta={beta:.2f},\ loc={loc:.2f}$')
plt.legend()
plt.title(r'ガンマ分布:2021年所得分布の近似')
plt.show()
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
実データを用いて統計的な取り組みを実践することは楽しいですか?
私は楽しいです!
今回は気合が入って長文になりました。
次回は推定の分野の最後の取り組みになります。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
この記事が気に入ったらサポートをしてみませんか?
