
7-4 捕獲再捕獲法信頼区間 ~ EXCEL・Pythonで捕獲再捕獲法をシミュレーション
今回の統計トピック
捕獲再捕獲法を学びます。
捕獲再捕獲法のシミュレーションにも挑戦します。
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
推定の分野
問4 捕獲再捕獲法信頼区間(池の魚)
試験実施年月
統計検定2級 2019年6月 問14(回答番号25)
問題
公式問題集をご参照ください。
解き方
題意
次の条件で母比率の 95%信頼区間を計算します。
・捕獲再捕獲法を実施
・母集団$${N}$$は十分大きい
・標本サイズ(再捕獲数)$${n=200}$$匹
・標本のうち印付きの数$${20}$$匹
図示します。

■母比率の信頼区間の公式(3つの近似)
母比率を$${p}$$、標本比率を$${\hat{p}}$$、標本サイズを$${n}$$とします。
3つの近似を用いて、次の母比率の信頼区間の公式を得ます。
【母比率の信頼区間の公式】
$$
\hat{p} - z_{\alpha/2}\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}} \leq p \leq \hat{p} +z_{\alpha/2}\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}\\
\\
または\\
\\
\hat{p} \pm z_{\alpha/2}\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}
$$
【3つの近似】
①母集団$${N}$$が十分大きい
無限母集団とみなして二項分布$${Bin(n, p)}$$に近似するものとして取り扱い、有限母集団修正を行わない。
②標本サイズ$${n}$$が十分大きい(その1)
二項分布に関する中心極限定理を用いて、$${z=\cfrac{\hat{p}-p}{\sqrt{p(1-p)/n}}}$$は近似的に標準正規分布に従うものとして取り扱う。
(ちなみに、$${p(1-p)/n}$$は標本比率$${\hat{p}}$$の分散)
③標本サイズ$${n}$$が十分大きい(その2)
$${\hat{p}}$$の標準偏差$${\sqrt{p(1-p)/n}}$$について、大数の法則を用いて$${p}$$を$${\hat{p}}$$に置き換えて、$${\hat{p}}$$の標準誤差の推定量$${\sqrt{\hat{p}(1-\hat{p})/n}}$$を利用する。
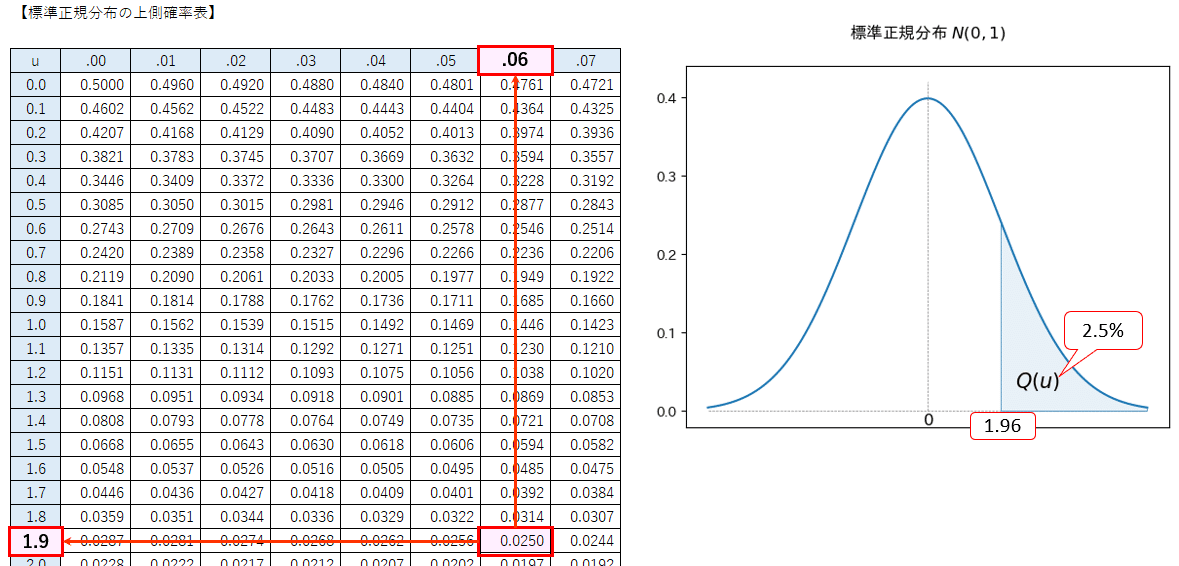
なお、$${z_{\alpha/2}}$$は標準正規分布の上側$${100 \alpha/2 \%}$$点です。
信頼係数が 95% の場合、標準正規分布の上側確率表より、$${z_{0.025}=1.96}$$です。
■信頼区間の計算
公式に標本比率を$${\hat{p}=20/100=0.1}$$、標本サイズを$${n=200}$$、上側確率2.5%点$${z_{0.025}=1.96}$$を当てはめて、信頼区間を計算します。
$$
\begin{align*}
&\hat{p} \pm z_{\alpha/2}\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}} \\
\\
&=0.1 \pm 1.96\sqrt{\cfrac{0.1 \times(1-0.1)}{200}} \\
\\
&=0.1 \pm 1.96\sqrt{\cfrac{0.1 \times 0.9}{200}} \\
\\
&=0.1 \pm 1.96 \times 0.0212 \\
\\
&=0.1 \pm 0.0415 \cdots
\end{align*}
$$
解答は$${0.100 \pm 0.042}$$です。
また、$${[0.058, 0.142]}$$と表記できます。
ちなみに、標準誤差の推定値は$${\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}=0.0212}$$です。
解答
② $${0.100 \pm 0.042}$$ です。
難易度 やさしい
・知識:母比率の信頼区間
・計算力:数式組み立て(低)、数式計算(低)
・時間目安:1分
知る
おしながき
公式問題集の問題に接近してみましょう!
今回は捕獲再捕獲法を深掘りしましょう。
捕獲再捕獲法
📕公式テキスト:掲載なし
総務省統計局の「なるほど統計学園」を参照して捕獲再捕獲法を確認しましょう。
「なるほど統計学園」では捕獲再捕獲法を次のように紹介しています。
個体数を把握する最も簡単な方法は、捕獲再捕獲法(標識再捕獲法とも言われます)と呼ばれる手法です。これは、一般に湖にいる魚などの生物に対して利用される方法です。
全体の個体数の推定
続いて「なるほど統計学園」は、全体の個体数を推定する方法を紹介しています。
ということで、「なるほど統計学園」にならって「問題を解く」の各数値から全体の個体数を推定してみましょう!
やりたいことを図示します。

全体の個体数を$${N}$$、最初の捕獲数を$${n_1}$$、再捕獲数を$${n_2}$$、再捕獲数のうち目印が付いている数を$${m}$$とします。
次のような割合の関係性に注目します。
$$
\begin{align*}
\cfrac{目印が付いている数m}{再捕獲数n_2}&=\cfrac{最初の捕獲数n_1}{全体の個体数N} \\
\\
全体の個体数N&=\cfrac{最初の捕獲数n_1 \times 再捕獲数n_2}{目印が付いている数m}
\end{align*}
$$
この式に、公式問題集の数値を当てはめてみましょう。
最初の捕獲数$${n_1=300}$$、再捕獲数$${n_2=200}$$、再捕獲数のうち目印が付いている数$${m=20}$$です。
$$
\begin{align*}
全体の個体数N&=\cfrac{最初の捕獲数n_1 \times 再捕獲数n_2}{目印が付いている数m} \\
\\
&=\cfrac{最初の捕獲数300 \times 再捕獲数200}{目印が付いている数20} \\
\\
&=\cfrac{60000}{20} \\
\\
&=3000
\end{align*}
$$
全体の個体数の推定値は 3,000匹 です。
約3,000匹の魚が生息する池・・・、きっと大きな池でしょう。

公式問題集の出題内容は、このような「全体の個体数の点推定」ではなく、「全体の個体数に占める目印を付けた個体数の比率(母比率)の区間推定」を行っている点に注意しましょう。
全体の個体数の区間推定
全体の個体数$${N}$$と、全体の個体数に占める最初の捕獲数の割合($${300/N}$$)という母比率$${p}$$の信頼区間を用いて、個体数の区間推定ができそうな予感です。
「問題を解く」の章で紹介した「母比率$${p}$$の信頼区間」の再登場です。
$$
\hat{p} - z_{\alpha/2}\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}} \leq p \leq \hat{p} +z_{\alpha/2}\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}} \\
\\
0.1-0.042 \leq p \leq 0.1+0.042 \\
\\
0.058 \leq p \leq 0.142 \\
$$
母比率$${p}$$の95%信頼区間は、$${0.058 \leq p \leq 0.142}$$です。
ここで母比率$${p}$$を全体の個体数に占める最初の捕獲数の割合$${300/N}$$に置き換えて、全体の個体数$${N}$$について解いてみましょう。
$$
0.058 \leq 300/N \leq 0.142 \\
\\
300/0.142 \leq N \leq 300/0.058 \\
\\
2112.6 \cdots \leq N \leq 5172.4 \cdots
$$
池に生息する全体の個体数の幅は、2112~5173匹のようです。
点推定値の3000匹に対して幅が3061匹。
幅がかなり広いです。
しかも、「2112~3000匹の間隔(888)」と「3000~5173匹の間隔(2173)」に偏りが生じている、という印象です。

「母比率の信頼区間」を利用して「個体数の区間を推定」する場合、この間隔の偏りに留意する必要がありそうです。
一応、検算しておきましょう。
「最初の捕獲数/全体の個体数」を計算します。
$$
300/2112 \fallingdotseq 0.142 \\
300/5173\fallingdotseq 0.058 \\
$$
$${0.058 \leq p \leq 0.142}$$と合致しました。
捕獲再捕獲法シミュレーション
全体の個体数の点推定と、全体の個体数に占める目印を付けた個体数の比率の区間推定について、EXCELでシミュレーションシートを作成しました。
このEXCELファイルは「EXCELで作成してみよう!」の項でダウンロードできます。
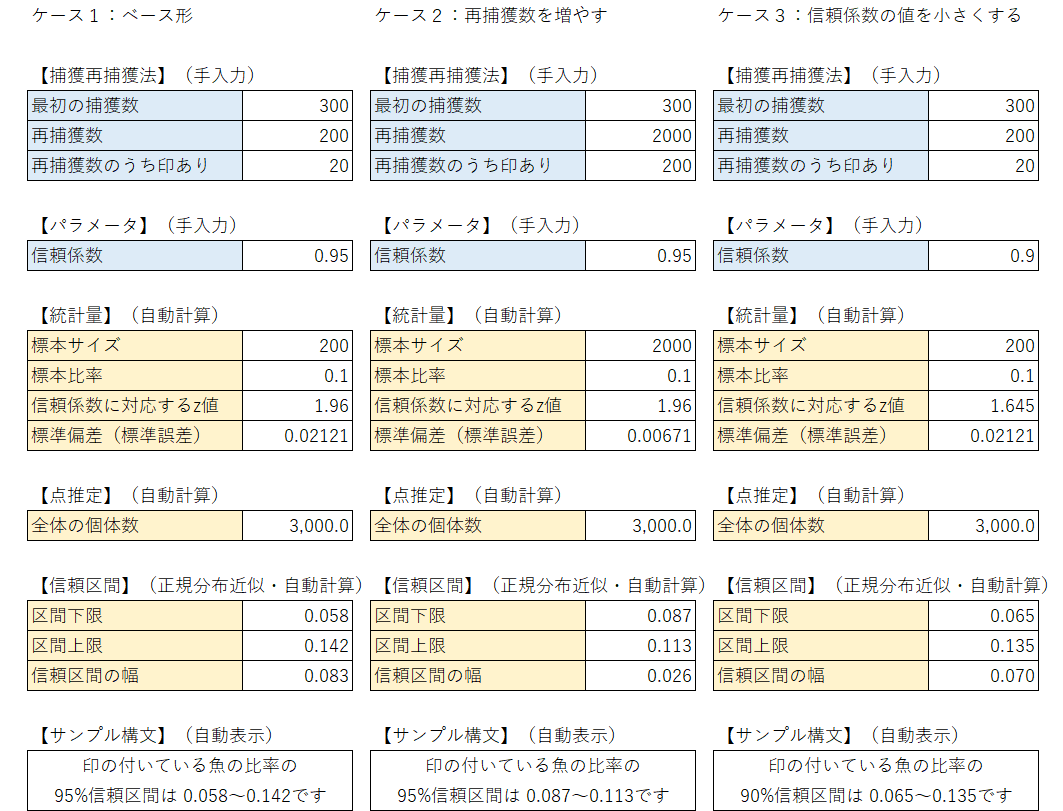
区間推定の計算に効くパラメータは、「再捕獲数(標本サイズ)」と「信頼係数(信頼係数に対応するz値)」の2つです。
この2つの値を変化させて、信頼区間の幅がどのように変化するか、確認しましょう。
ケース2:再捕獲数を増やす
再捕獲数を増やすと信頼区間の幅が小さくなります。
再捕獲数を増やすと、母比率の信頼区間の公式$${\hat{p} \pm z_{\alpha/2}\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}}$$の分母の$${n}$$が大きくなるので、計算結果の値は小さくなります。
【結論】
再捕獲数(標本サイズ)を増やすと信頼区間の幅は小さくなり、減らすと幅は大きくなります。
ケース3:信頼係数の値を小さくする
信頼係数の値を小さくすると、信頼区間の幅が小さくなります。
信頼係数を小さくすると、信頼係数に対応する$${z}$$値が小さくなります。
母比率の信頼区間の公式$${\hat{p} \pm z_{\alpha/2}\sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}}$$の$${z_{\alpha/2}}$$が小さくなるので、計算結果の値は小さくなります。
【結論】
信頼区間の値を小さくすると信頼区間の幅は小さくなり、大きくすると幅は大きくなります。
母比率の区間推定
母比率の区間推定に関する詳細な記事を「6-1 標本割合の標本分布」で書いています。
よかったら覗いていってくださいね!
実践する
捕獲再捕獲法シミュレーションしてみよう!
今回は「知る」の章で触れた捕獲再捕獲法シミュレーションを実践してみましょう。
EXCELとPythonで少し趣向を変えてみます。
EXCELは「知る」の章で用いたシート、Pythonは捕獲再捕獲法を実施するコードです。
電卓・手作業で作成してみよう!
「知る」の章に掲載のシミュレーションシートと、母比率の信頼区間の公式を用いて、再捕獲数・印の付いた数・信頼係数に応じた母比率の信頼区間を手作業で計算してみましょう!
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。
EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。
シミュレーションシートの紹介
「最初の捕獲数」「再捕獲数」「再捕獲数のうちの印ありの数」「信頼係数」の欄にさまざまな値を設定して、母比率の信頼区間がどのように変化するか、いろいろ確認してみてください。

計算内容の補足(信頼係数に対応するz値)
NORM.S.INV関数で確率に対応する標準正規分布のz値(パーセント点)を取得します。
引数は、=NORM.S.INV( 確率 ) です。

このシートでは、下側確率の z値(パーセント点)を算出して、式の頭にマイナスを付けて、上側確率に変換しています。
下の図を用いてもう少し具体的に説明します。

信頼係数 95% の場合、下側確率のz値(パーセント点)は$${-1.96}$$です。
マイナスすると上側確率のz値(パーセント点)$${1.96}$$になります。
なお、=NORM.S.INV( 0.975 )とすると、上側確率のz値(パーセント点)の$${1.96}$$を取得できます。
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回は、①母比率の信頼区間の計算と、②捕獲再捕獲法シミュレーションを実施します。
①インポート
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline②母比率の信頼区間の計算(正規分布近似)
母比率の信頼区間を計算する関数を定義します。
引数は 標本サイズ n、標本比率 p_hat、信頼係数 vl_cf です。
標本比率の標準偏差 stddev を計算してから、 scipy.statsの norm.interval で信頼区間の下限・上限を取得して、戻り値にしています。
引数は、norm.interval( confidence=信頼係数, loc=平均, scale=標準偏差 ) です。
### 母比率の信頼区間計算関数
# 引数 n=標本サイズ、p_hat=標本比率、val_cf=信頼係数
def calc_pop_prop_confidence_interval(n, p_hat, val_cf):
# 標準誤差の計算
stddev = np.sqrt(p_hat * (1 - p_hat) / n)
# 戻り値:正規分布の信頼区間[a,b](タプル) loc=標本比率、scale=標準誤差
return norm.interval(confidence=val_cf, loc=p_hat, scale=stddev)信頼区間の取得を実行します。
設定値を変えてみて、さまざまな信頼区間を確認してみましょう。
# 設定 n:標本サイズ、p_hat=標本比率、cf=信頼係数
n, p_hat, val_cf = 200, 0.1, 0.95
# 母比率の信頼区間の取得と結果表示
ci_lower, ci_upper = calc_pop_prop_confidence_interval(n, p_hat, val_cf)
print(f'標本サイズ {n}, 標本比率 {p_hat}, 正規分布近似のとき\n'
f'母比率の {val_cf*100}%信頼区間は [{ci_lower:.3f}, {ci_upper:.3f}]')
③捕獲再捕獲法シミュレーション
捕獲→目印付け→戻す→再捕獲→目印のカウント→信頼区間計算を行う関数を定義します。
目印は総数N匹の10倍の数値を加算することにします。
np.random.choiceで母集団all_fishからランダムに捕獲・再捕獲します。
### 捕獲再捕獲法シミュレーション関数
# 引数:num_all=総数、num_capture=最初の捕獲数、num_recapture=再捕獲数、val_cf=信頼係数
def capture_recapture_method(num_all, num_capture, num_recapture, val_cf, disp=True):
### 初期値設定
mark = num_all * 10 # 目印:総数N匹の10倍の数値
all_fish = np.arange(1, num_all+1) # 母集団・総数N匹の生成:1からNまでの連番
### 捕獲再捕獲法の処理
# 1.母集団からランダムに捕獲:num_capture匹
captured_fish = np.random.choice(all_fish, num_capture, replace=False)
all_fish = np.delete(all_fish, captured_fish-1) # 第2引数:削除する要素のindex
# 2.目印を付与:目印markの値を加算
captured_fish_marked = captured_fish + mark
# 3.母集団に戻す
all_fish = np.hstack([all_fish, captured_fish_marked])
# 4.母集団からランダムに再捕獲:num_recapture匹
recaptured_fish = np.random.choice(all_fish, num_recapture, replace=False)
# 5.目印数をカウント(markの値より大きい魚:Trueを合計する)
num_recap_fish_marked = np.sum(recaptured_fish > mark)
### 信頼区間の表示
if not disp: # disp=Falseの時、信頼区間表示を省略
pass
elif not num_recap_fish_marked: # 目印数=0の時、信頼区間表示を中止
print('再捕獲時の目印数が0のため、信頼区間の計算を中止します')
else: # 目印数≠0の時、信頼区間を表示
# 標本比率の計算
p_hat = num_recap_fish_marked / num_recapture
# 信頼区間の取得
ci_lower, ci_upper = calc_pop_prop_confidence_interval(num_recapture,
p_hat, val_cf)
# 信頼区間の表示
print(f'再捕獲数 {num_recapture}, 再捕獲時の目印数 {num_recap_fish_marked}, '
f'標本比率 {p_hat}, 正規分布近似のとき,\n'
f'母比率の {val_cf*100}%信頼区間は [{ci_lower:.3f}, {ci_upper:.3f}]')
# 戻り値:再捕獲時の目印数
return num_recap_fish_marked捕獲再捕獲法をシミュレーションしてみましょう。
この例では、総数N=3000匹、最初の捕獲数(目印を付ける数)num_cap=300匹、再捕獲数num_recap=200、信頼係数val_cf=0.95としました。
他の値でも試してみてくださいね。
# 設定:N=総数、num_cap=最初の捕獲数、num_recap=再捕獲数、val_cf=信頼係数
N, num_cap, num_recap, val_cf = 3000, 300, 200, 0.95
# 乱数シードの設定
np.random.seed(2)
# 捕獲再捕獲法の実施
num_recap_fish_marked = capture_recapture_method(N, num_cap, num_recap, val_cf)
乱数シードを2にすると、再捕獲時の目印数が公式問題集の結果と同じ 20 になります。
乱数シードを変えると、再捕獲時の目印数がランダムに変わります。
再捕獲時の目印数は確率変数なんですね。
④捕獲再捕獲法を繰り返し試行して目印数のヒストグラムを描画
上記の捕獲再捕獲法をたくさん繰り返し実行して、ランダムに決まる「再捕獲時の目印数のヒストグラム」を描画します。
この例では1000回繰り返し実行します。
# 設定:N=総数、num_cap=最初の捕獲数、num_recap=再捕獲数、val_cf=信頼係数
N, num_cap, num_recap, val_cf = 3000, 300, 200, 0.95
# 設定:試行数、乱数シード
num_trial = 1000
np.random.seed(7)
# 捕獲再捕獲法を試行数、繰り返し試行
trial_result_list = []
for i in range(num_trial):
trial_result_list.append(capture_recapture_method(N, num_cap, num_recap,
val_cf, disp=False))
# ヒストグラムのプロット
plt.hist(trial_result_list, bins='auto')
plt.xlabel('再捕獲時の目印の数')
plt.ylabel('度数')
plt.title(f'捕獲再捕獲法を{num_trial}回試行(総数{N}, 捕獲数{num_cap}, '
f'再捕獲数{num_recap})')
plt.show()
なんとなく、正規分布に近い感じがしないでもないですね。
10匹以下しか捕獲できないとき、35匹以上捕獲できるとき、など、再捕獲時に得られる目印数にばらつきがあります。
公式問題集の目印数の割合(母比率)の95%信頼区間にそれなりの幅があることは、このバラツキからも想像できる感じがします。
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
「捕獲再捕獲法」で検索すると多くのWebサイトがヒットします。
統計のメジャーなジャンルのようですね。
統計の実務例に接することができるのは嬉しいです。
統計が身近に感じられます。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
この記事が気に入ったらサポートをしてみませんか?
