
7-3 母比率pが未知の標本サイズ ~ 母比率の最低標本サイズの計算
今回の統計トピック
母比率の区間推定の公式を利用して標本調査の最低標本サイズを計算します。
EXCEL、Pythonを活用して、母比率の区間推定と標本サイズを実際に求めてみましょう!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
推定の分野
問3 $${p}$$が未知の標本サイズ(政策支持率の標本調査)
試験実施年月
統計検定2級 2019年11月 問15(回答番号25)
問題
公式問題集をご参照ください。
解き方
題意
母比率$${p}$$の信頼区間を応用して標本サイズを計算する問題です。
次の条件の下、最低標本サイズを計算します。
・タスク:政策支持率の区間推定
・母集団:10万人以上
・母比率:未知
・信頼係数:95%
・信頼区間の幅:6%以下
・他の条件
・標本抽出方法は単純無作為抽出法
・回答率は100%を仮定
・二項分布は近似的に正規分布に従う

■【条件】母集団が10万人以上
母集団の大きさ$${N}$$が十分大きく、標本(標本サイズ$${n}$$)は互いに独立であるので(ベルヌーイ試行)、標本のうち政策を支持する人の数$${x}$$は二項分布$${Bin(n, p)}$$に従うと想定できます。
■標本比率の期待値と分散
二項分布の母比率$${p}$$の推定量である「標本比率」$${\hat{p}=\cfrac{x}{n}}$$について、期待値$${E[\hat{p}]=p}$$、分散$${V[\hat{p}]=\cfrac{p(1-p)}{n}}$$です。
■【条件】二項分布は近似的に正規分布に従う
標本比率$${\hat{p}=\cfrac{x}{n}}$$を標準化した$${z=\cfrac{\hat{p}-p}{\sqrt{\cfrac{p(1-p)}{n}}}}$$は近似的に標準正規分布に従います。

■母比率の信頼区間
標準正規分布の上側$${100\alpha/2%}$$点を$${z_{\alpha/2}}$$とすると、母比率$${p}$$の信頼区間は次の式になります。
$${\hat{p}-z_{\alpha/2}\sqrt{\cfrac{p(1-p)}{n}} \leq p \leq \hat{p}+z_{\alpha/2}\sqrt{\cfrac{p(1-p)}{n}}}$$
■信頼区間の幅
信頼区間は$${\hat{p}-z_{\alpha/2}\sqrt{\cfrac{p(1-p)}{n}}}$$から$${\hat{p}+z_{\alpha/2}\sqrt{\cfrac{p(1-p)}{n}}}$$です。
$${\hat{p}}$$を挟んでマイナス方向とプラス方向に$${z_{\alpha/2}\sqrt{\cfrac{p(1-p)}{n}}}$$ですので、信頼区間の「幅」は$${2\times z_{\alpha/2}\sqrt{\cfrac{p(1-p)}{n}}}$$です。
問題文から、この「幅」が$${6\%}$$以下になることを目指します!

■標本サイズの計算に必要な値1:$${z_{\alpha/2}}$$
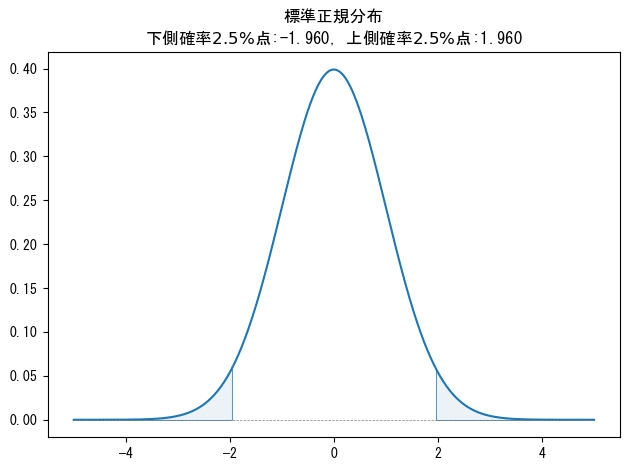
標準正規分布の上側$${100\alpha/2%}$$点の$${z_{\alpha/2}}$$は、信頼係数が95%なので、上側$${100\alpha/2\%}$$点$${=100\times(1-0.95)/2=}$$上側$${2.5\%}$$点です。
上側$${2.5\%}$$点は、$${z_{\alpha/2}=1.96}$$です。

■標本サイズの計算に必要な値2:$${p}$$
母比率$${p}$$は未定です。
標本サイズの見積り数が過小になることを避けるべく安全をもたせる場合、$${p(1-p)}$$の値が最大になる$${p=0.5}$$を選択します。

■標本サイズの計算
信頼区間の幅が$${0.06}$$以下になる標本サイズ$${n}$$を計算します。
$$
\begin{align*}
2\times z_{\alpha/2}\sqrt{\cfrac{p(1-p)}{n}} &\leq 0.06 \\
2\times 1.96 \times \sqrt{\cfrac{0.5(1-0.5)}{n}} &\leq 0.06 \\
2\times 1.96 \times \sqrt{\cfrac{0.5 \times 0.5}{n}} &\leq 0.06 \\
2\times 1.96 \times \cfrac{0.5}{\sqrt{n}} &\leq 0.06 \\
1.96 \times \cfrac{1}{\sqrt{n}} &\leq 0.06 \\
\sqrt{n} &\geq\cfrac{1.96}{0.06} \\
n &\geq \left(\cfrac{1.96}{0.06} \right)^2 \\
\\
n &\geq 1067.1 \cdots
\end{align*}
$$
標本サイズ$${n}$$は 1,068 以上です。
解答選択肢の中で、この値以上の最小値は 1,100 です。
解答
④ 1100 です。
難易度 ふつう
・知識:母比率の信頼区間、標本サイズ計算
・計算力:数式組み立て(中)、数式計算(低)
・時間目安:2分
知る
おしながき
公式問題集の問題に接近してみましょう!
正規分布近似できる場合の母比率の標本サイズを計算しましょう。
母集団が多いことと、有限母集団修正をしないことが計算の前提条件になります。
母比率の標本サイズ計算式
母比率の信頼区間の幅の計算式を標本サイズ$${n}$$について解いて、最低標本サイズの計算式を得ます。
また、信頼区間の幅を$${w}$$とします。
$$
2\times z_{\alpha/2}\sqrt{\cfrac{p(1-p)}{n}}=w \\
\\
2\ z_{\alpha/2}\cfrac{\sqrt{p(1-p)}}{\sqrt{n}}=w \\
\\
\sqrt{n}=\cfrac{2\ z_{\alpha/2}\sqrt{p(1-p)}}{w} \\
\\
n= \left(\cfrac{2\ z_{\alpha/2}\sqrt{p(1-p)}}{w} \right)^2 \\
\\
n= \left(\cfrac{2\ z_{\alpha/2}}{w} \right)^2 p(1-p) \\
$$
最低標本サイズは$${n= \left(\cfrac{2\ z_{\alpha/2}}{w} \right)^2 p(1-p)}$$です。
母比率$${p=0.5}$$、信頼係数$${95\%}$$、信頼区間の幅$${w=6\%}$$で最低標本サイズを計算してみましょう。
上側確率2.5%点は1.96です。
$$
n= \left(\cfrac{2\ z_{\alpha/2}}{w} \right)^2 p(1-p) \\
\\
n= \left(\cfrac{2\times 1.96}{0.06} \right)^2 0.5(1-0.5) \\
\\
n= \left(\cfrac{2\times 1.96}{0.06} \right)^2 0.5^2 \\
\\
n= \left(\cfrac{2\times 1.96 \times 0.5}{0.06} \right)^2 \\
\\
n= \left(\cfrac{1.96}{0.06} \right)^2 \\
\\
n=1067.1\cdots
$$
最低標本サイズは 1,068 です。
母比率・信頼係数・信頼区間の幅を変えて計算してみる
EXCELで計算シートを作成しました。

■母比率の変動の影響
母比率を下げると、標本サイズは小さくなります。
母比率を上げても、標本サイズは小さくなります。

「問題を解く」で安全をみて$${p(1-p)}$$が最大になる0.5を採用したのは、母比率0.5のときに標本サイズが最大になるからです!
■信頼係数の変動の影響
信頼係数を上げると、標本サイズは大きくなります。
信頼係数を下げると、標本サイズは小さくなります。

■信頼区間の幅の変動の影響
信頼区間の幅を狭めると、標本サイズは大きくなります。
信頼係数の幅を広げると、標本サイズは小さくなります。

信頼係数や信頼区間の幅を操作して推定の精度を上げる場合には、最低標本サイズが大きくなる点に留意する必要があります。
実践する
母比率の最低標本サイズを計算してみよう!
「知る」の計算式を利用して、手作業で計算、EXCELの計算シートで計算、Pythonのコードで計算しましょう。
電卓・手作業で作成してみよう!
「知る」に掲載の計算式を利用して、電卓やそろばんをはじいて、手作業で母比率の最低標本サイズを計算してみましょう!
母比率、信頼係数(標準正規分布の上側確率のパーセント点)、信頼区間の幅に、さまざまな値を設定して、最低標本サイズの動きを確認しましょう。
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。
EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。
計算シートの紹介

「知る」の計算式をEXCELの計算式に当てはめました。
信頼係数から標準正規分布の上側パーセント点を取得する「NORM.S.INV関数」を利用しています。
引数は =NORM.S.INV( 確率 ) です。
確率の部分には「下側確率」になるように計算式を設定しています。
信頼係数95%の場合、上側確率は2.5%となり、下側確率は97.5%(100-上側確率)です。

3つの表を横並びにしています。
母比率・信頼係数・信頼区間の幅の値をいろいろと変えてみて、最低標本サイズがどのように変わるか、動きを確認しましょう。
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回は、母比率の最低標本サイズを計算します。
①インポート
import numpy as np
from scipy.stats import norm, binom
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline②母比率の最低標本サイズの計算(正規分布近似)
最低標本サイズ$${n}$$、標準正規分布の上側確率%点$${z_{\alpha/2}}$$(信頼係数$${cf}$$)、信頼区間の幅$${w}$$、母比率$${p}$$、回答回収率$${r}$$のとき、
$${n= \left\{ \left( \cfrac{2z_{\alpha/2}}{w} \right)^2 p (1-p) \right\} /r }$$を計算します。
■最低標本サイズ計算関数の定義
「norm.ppf((1+cf)/2」で上側確率%点$${z_{\alpha/2}}$$を取得しています。
# 最低標本サイズ計算関数
def sample_size_calc(p, cf, w, r):
return int(np.ceil((((2 * norm.ppf((1+cf)/2, 0, 1))/w)**2 * p * (1-p))/r))■最低標本サイズの計算
設定値を変えて、さまざまな標本サイズを計算しましょう。
# 設定: p=母比率、cf=信頼係数、w=信頼区間の幅、r=回答回収率
p, cf, w, r = 0.5, 0.95, 0.06, 1
# 計算実行
print(f'母比率:{p*100}%、信頼係数:{cf*100}%、幅:{w*100}%、回答回収率:{r*100}%')
print(f'最低標本サイズ: {sample_size_calc(p, cf, w, r):,}個')
以下は記事の図表作成用のサンプルコードです。
③二項分布の正規分布近似
# 二項分布の確率質量関数b、正規分布の確率密度関数nの取得
x =np.linspace(0, 10, 1001)
b = binom.pmf(x, n=10, p=0.5)
n = norm.pdf(x, loc=5, scale=1.6)
# 描画
fig, ax = plt.subplots(1, 2, figsize=(8, 3), sharey=True)
ax[0].bar(x, b, width=0.3)
ax[0].set_title('二項分布')
ax[0].set_xticks([]), ax[0].set_yticks([])
ax[1].plot(x, n)
ax[1].set_title('標準正規分布')
ax[1].set_xticks([]), ax[1].set_yticks([])
plt.show()
④標準正規分布の上側・下側100α/2%点
■プロット用の関数の定義
# プロット関数
def norm_dist_cf_bothside(mu, stddev, cf, x_min, x_max):
# 確率密度関数の値の取得
x = np.linspace(x_min, x_max, 1001) # 確率変数 X の値を取得
y = norm.pdf(x, mu, stddev) # 確率密度関数f(x)の値を取得
# 上側確率、下側確率のパーセント点の取得
pp_upp = norm.ppf((1+cf)/2, mu, stddev) # 上側確率
pp_low = norm.ppf((1-cf)/2, mu, stddev) # 下側確率
# 描画区間の値の取得
y0 = 0 # y=0
color = 'steelblue'
x_draw1 = np.linspace(x_min, pp_low, 1001) # 区間[x_min, pp_low]の変数Xの値を取得
y_draw1 = norm.pdf(x_draw1, mu, stddev) # 区間[x_min,pp_low]の関数f(x)の値を取得
x_draw2 = np.linspace(pp_upp, x_max, 1001) # 区間[pp_upp, x_max]の変数Xの値を取得
y_draw2 = norm.pdf(x_draw2, mu, stddev) # 区間[pp_upp, x_max]の関数f(x)の値を取得
# プロット処理
plt.plot(x, y) # 確率密度関数の描画
plt.hlines(y0, x_min, x_max, lw=0.5, # y=0の水平点線の描画 x_min≦X≦x_max
color='gray', ls='--')
plt.fill_between(x_draw1, y_draw1, y0, # 区間[x_min,pp_low]の塗りつぶし描画
color=color, alpha=0.1)
plt.fill_between(x_draw2, y_draw2, y0, # 区間[pp_upp, x_max]の塗りつぶし描画
color=color, alpha=0.1)
plt.hlines(y0, x_min, pp_low, lw=0.5) # y=0の水平線の描画 x_min≦X≦pp_low
plt.hlines(y0, pp_upp, x_max, lw=0.5) # y=0の水平線の描画 pp_upp≦X≦x_max
plt.vlines(pp_low, y0, y_draw1[-1], lw=0.5) # x=pp_lowの垂直線の描画
plt.vlines(pp_upp, y0, y_draw2[0], lw=0.5) # x=pp_uppの垂直線の描画
# 修飾
plt.title(f'標準正規分布\n'
f'下側確率${(1-cf)/2*100:.1f}\%$点:{pp_low:.3f}, '
f'上側確率${(1-cf)/2*100:.1f}\%$点:{pp_upp:.3f}')
plt.tight_layout()
plt.show()■プロット処理
cf(信頼係数)、描画区間(x_min、x_max)を設定値を変えると、グラフの上側・下側確率%点、上側・下側確率の領域、描画域が変化します。
# 【設定】
# mu=標準正規分布の平均、stddev=標準偏差、cf=信頼係数、描画区間[x_min,x_max]
mu, stddev, cf = 0, 1, 0.95
x_min, x_max = -5, 5
# プロット処理の実行
norm_dist_cf_bothside(mu, stddev, cf, x_min, x_max)
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
公式問題集CBT対応版で取り扱う区間推定のうち、区間を計算するのは「母比率」「母比率の差」だけのようです。
公式テキストでは、上記の他にたくさんの区間推定を取り扱っています。
・母平均(母分散既知):標準正規分布
・母平均(母分散未知):$${t}$$分布
・母分散:$${\chi^2}$$分布
・母平均の差(母分散既知):標準正規分布
・母平均の差(母分散未知で等しい):$${t}$$分布、プールした分散
・母平均の差(対応のある2標本):$${t}$$分布
・母分散の比:$${F}$$分布
過去問(2018~2021年)では、確かに母比率以外の区間推定が出題されにくい感じです。
※母比率以外の区間推定の出題
・2021年6月問15 母平均(母分散既知)
・2019年11月問14 母平均(非正規母集団)
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
この記事が気に入ったらサポートをしてみませんか?
