
7-6 母比率の差の信頼区間と検定 〜 スポーツ世論調査
今回の統計トピック
母比率の差の95%信頼区間を用いて、母比率の差の検定を行います。
統計的仮説検定の先取りをいたします!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
知る+問題を解く
📘公式問題集のカテゴリ
推定の分野
問6 母比率の差の区間推定と検定(スポーツ国際大会の関心)
試験実施年月
統計検定2級 2017年11月 問13(回答番号28)
問題
公式問題集をご参照ください。
解き方
題意
母比率の差の95%信頼区間を用いて、次の2つデータの「母比率$${p_1,p_2}$$の差がゼロである」(割合が変化していない)という帰無仮説を有意水準5%で検定します。
【データ1】
・標本サイズ$${n_1=1897}$$
・標本比率$${\hat{p_1}=0.483}$$
【データ2】
・標本サイズ$${n_2=1925}$$
・標本比率$${\hat{p_2}=0.416}$$
問題の概要を図示します。

今回の記事の構成
この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」と「知る」の章を1つの章にまとめます。
最初は「知る」のゾーンです。
母比率の差の信頼区間の概要を確認しましょう。
その後、「問題を解く」のゾーンに移ります。
なお、問題を解く部分のみ読みたい場合は、見出し【必須】の項目をお読みください。【任意】は飛ばしていただいて大丈夫です。
続いて「実践する」の章では「母比率の差の信頼区間の公式」をPythonで実装します。
母比率の差の信頼区間
📕公式テキスト:3.5.4 母比率の差の区間推定(127ページ~)
【必須】母比率の差の信頼区間の公式
母比率の差の信頼区間の公式は次のとおりです。
$$
(\hat{p_1}-\hat{p_2}) \pm z_{\alpha/2} \sqrt{\cfrac{\hat{p_1}(1-\hat{p_1})}{n_1}+\cfrac{\hat{p_2}(1-\hat{p_2})}{n_2}}
$$
数直線で表します。

母比率の差$${\hat{p}_1-\hat{p}_2}$$の前後に$${z_{\alpha/2} \sqrt{\cfrac{\hat{p_1}(1-\hat{p_1})}{n_1}+\cfrac{\hat{p_2}(1-\hat{p_2})}{n_2}}}$$の幅を持ちます。
続いて、上の公式の成り立ちに触れます。
読み飛ばしても大丈夫です。
【任意】母比率の差の信頼区間の公式の成り立ち
2つのデータは別個に「単純無作為抽出されたもの」であり、独立である(対応関係は無い)、と想定します。
①二項分布近似、②正規分布近似、③母比率を標本比率に置き換え、の3つ近似を用います。
①二項分布近似
母集団が大きいとき、無限母集団とみなして、2つのデータの確率変数$${x_1,\ x_2}$$が二項分布$${Bin(n_1, p_1), Bin(n_2, p_2)}$$に従うと想定します。
$${x_1}$$と$${x_2}$$の期待値と分散は次のとおりです。
・期待値:$${E[x_1]=n_1p_1, \quad E[x_2]=n_2p_2}$$
・分散:$${V[x_1]=n_1p_1(1-p_1), \quad V[x_2]=n_2p_2(1-p_2)}$$
②正規分布近似
標本サイズが大きいとき、中心極限定理を利用して、2つのデータの標本比率は近似的に正規分布に従うと想定します。
$$
\hat{p_1}=\cfrac{x_1}{n_1} \sim N \left(p_1, \cfrac{p_1(1-p_1)}{n_1} \right) \\
\\
\hat{p_2}=\cfrac{x_2}{n_2} \sim N \left(p_2, \cfrac{p_2(1-p_2)}{n_2} \right) \\
$$
標本比率$${\hat{p_1}, \hat{p_2}}$$の平均(期待値)と分散は次のとおりです。
・平均(期待値):$${p_1, \quad p_2}$$
・分散:$${p_1(1-p_1)/n_1, \quad p_2(1-p_2)/n_2}$$
2つのデータの標本比率の差$${\hat{p_1}-\hat{p_2}}$$は正規分布の再生性の性質から、次の正規分布に従います。
$$
\hat{p_1}-\hat{p_2} \sim N \left(p_1-p_2,\ \cfrac{p_1(1-p_1)}{n_1}+\cfrac{p_2(1-p_2)}{n_2} \right)
$$
【差の平均、差の分散の補足】
2つの確率変数の差の平均(期待値)は、$${E[aX+bY]=aE[X]+bE[Y]}$$より、$${E[1X+(-1)Y]=1E[X]+(-1)E[Y]=E[X]-E[Y]}$$(平均の引き算)になります。
したがって、2つのデータの「差の平均(期待値)」は$${p_1-p_2}$$です。
一方で、2つの確率変数の差の分散は、$${V[aX+bY]=a^2V[X]+b^2V[Y]}$$より、$${V[1X+(-1)Y]=1^2V[X]+(-1)^2V[Y]=V[X]+V[Y]}$$(分散の足し算)になります。
したがって、2つのデータの「差の分散」は$${\cfrac{p_1(1-p_1)}{n_1}+\cfrac{p_2(1-p_2)}{n_2}}$$です。
そして標準化します。
確率変数$${\hat{p_1}-\hat{p_2}}$$、平均$${p_1-p_2}$$、標準偏差$${\sqrt{p_1(1-p_1)/n_1+p_2(1-p_2)/n_2}}$$を用います。
$$
z=\cfrac{(\hat{p_1}-\hat{p_2})-(p_1-p_2)}{\sqrt{p_1(1-p_1)/n_1+p_2(1-p_2)/n_2}} \sim N(0,1)
$$
標準正規分布の上側$${100\alpha/2 \%}$$点を$${z_{\alpha/2}}$$とし、確率$${100(1-\alpha) \%}$$は次のように表せます。
$$
\begin{align*}
P \biggl( &(\hat{p_1}-\hat{p_2}) - z_{\alpha/2} \sqrt{\cfrac{p_1(1-p_1)}{n_1}+\cfrac{p_2(1-p_2)}{n_2}} \\
&\leq p_1-p_2 \leq \\
&(\hat{p_1}-\hat{p_2}) + z_{\alpha/2} \sqrt{\cfrac{p_1(1-p_1)}{n_1}+\cfrac{p_2(1-p_2)}{n_2}} \biggr) \\
=&1-\alpha \\
\end{align*}
$$
③母比率を標本比率に置き換え
標本サイズが大きいとき、大数の法則を利用して、標準偏差に含まれる母比率$${p_1,p_2 }$$を推定値$${\hat{p_1}, \hat{p_2}}$$に置き換えて、信頼区間の公式の完成です。
$$
(\hat{p_1}-\hat{p_2}) \pm z_{\alpha/2} \sqrt{\cfrac{\hat{p_1}(1-\hat{p_1})}{n_1}+\cfrac{\hat{p_2}(1-\hat{p_2})}{n_2}}
$$

問題を解く
問題に戻ります。
【必須】95%信頼区間の計算
母比率の差の信頼区間の公式に標本比率、標本サイズ、標準正規分布の上側2.5%点$${z_{0.025}=1.96}$$を当てはめて、95%信頼区間を計算します。
$$
\begin{align*}
&(\hat{p_1}-\hat{p_2}) \pm z_{\alpha/2} \sqrt{\cfrac{\hat{p_1}(1-\hat{p_1})}{n_1}+\cfrac{\hat{p_2}(1-\hat{p_2})}{n_2}} \\
\\
&=(0.483-0.416) \pm 1.96\sqrt{\cfrac{0.483\times(1-0.483)}{1897}+\cfrac{0.416\times(1-0.416)}{1925}} \\
\\
&=0.067 \pm 1.96\sqrt{\cfrac{0.483\times0.517}{1897}+\cfrac{0.416\times0.584}{1925}} \\
\\
&= 0.067 \pm 0.031\cdots \\
\\
&=[ 0.036, 0.098 ] \\
\end{align*}
$$
母比率の差の95%信頼区間は$${0.067 \pm 1.96\sqrt{\cfrac{0.483\times0.517}{1897}+\cfrac{0.416\times0.584}{1925}}}$$であり、値は$${[0.036, 0.098]}$$です。
(ア)の解答は、$${0.067 \pm 1.96\sqrt{\cfrac{0.483\times0.517}{1897}+\cfrac{0.416\times0.584}{1925}}}$$です。
【必須】割合が変化したと言えるかどうか
母比率の差の95%信頼区間は$${[0.036, 0.098]}$$です。
95%信頼区間にゼロを含まないので、有意水準5%で「割合が変化したと言ええる」(母比率の差はゼロではない)という結論が導かれます。
(イ)の解答は「言える」です。
【任意】95%区間にゼロを含むかどうかの意味合い
平成25年(2013年)の48.3%と平成21年(2009年)の41.6%の比率の差「6.7%」について、「割合が変化したと言えるかどうか」は、「2つの母比率の差がゼロか、ゼロでないか」を「検定」して判断します。
ここでは「割合が変化した=差がゼロではない」ことを確認したい仮説とします。
まず、確認したい仮説と逆向きの仮説「割合が変化していない」=「母比率の差がゼロである:$${p_1-p_2=0}$$」を立てます。
この逆向きの仮説のことを帰無仮説と呼びます。
そして帰無仮説と対立するのが、その名の通り対立仮説です。
対立仮説は確認したい仮説「割合が変化した」=「母比率の差がゼロではない:$${p_1-p_2\neq0}$$」です。
95%信頼区間を用いて検定する場合は、95%信頼区間に対応する有意水準5%を用いて、次のように検定を行います。
(100%-95%=5%)
■95%信頼区間に帰無仮説の値「差がゼロ」を含む場合(下図の②)
95%信頼区間に含まれるがゆえに「差がゼロ」の主張を覆せないだろうと考えます。
このことは、標本から得た比率の差「6.7%」はたまたま起きたことだ、母比率の差がゼロであることを否めない、と考えることと同じです。
従いまして、有意水準5%で有意差があるとは言えず、帰無仮説「割合が変化していない」を受容します。
■95%信頼区間に帰無仮説の値「差がゼロ」を含まない場合(下図の①③)
帰無仮説の主張する「差がゼロ」は95%信頼区間から外れているので、「差がゼロ」とは言えないだろうと考えます。
このことは、標本から得た比率の差「6.7%」は偶然起きたのではなく「意味の有る差」であり、有意水準5%で「有意差がある」と判断することに繋がります。
有意差があるので帰無仮説を棄却して、対立仮説「割合が変化した」を採択します。
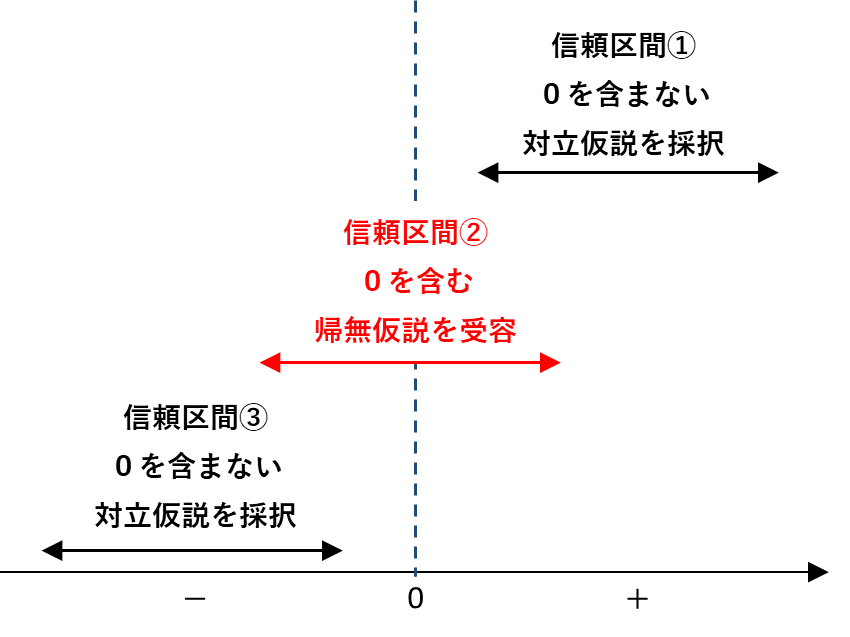
(まとめ)
母比率の差の95%信頼区間にゼロを含む場合、有意水準5%で割合が変化したと言えない(帰無仮説を受容)。
母比率の差の95%信頼区間にゼロを含まない場合、有意水準5%で割合が変化したと言える(帰無仮説を棄却・対立仮説を採択)。
解答
② です。
難易度 ふつう
・知識:母比率の差の信頼区間、信頼区間を用いた検定
・計算力:数式組み立て(低)、数式計算(低)
・時間目安:1分
日本人選手がスポーツ国際大会で活躍することの関心の調査
公式問題集では、文部科学省の「体力・スポーツに関する世論調査」の結果を用いて問題を構成しています。
スポーツ国際大会で日本人選手が活躍することに「非常に関心がある」と回答した人の割合が、平成21年(2009年)1月調査から平成25年(2013年)1月調査の間で変化したかについて、統計的仮説検定を用いて、6.7%の割合増加は「変化したと言える」と結論付けました。
この期間には、サッカー、野球、ソフトボール、ゴルフ、フィギュアスケートなどの種目で日本人選手が世界の舞台で大活躍をしています。

2013年以降の状況はどうでしょう。
日本人選手がどんどん世界のフィールドで活躍しています。
東京オリンピック・パラリンピック大会も開催されました。
「非常に関心がある」人の割合はもっと増えているような気がします。
ぜひとも数値を確かめたいと、最新の調査を探したところ、「体力・スポーツに関する世論調査」は2013年で終了していました・・・(泣)
代わりに、スポーツ庁(2015年設置)が装い新たにして、毎年「スポーツの実施状況等に関する世論調査」を行っています。
最新は令和4年調査です。
次のスポーツ庁のWEBサイトで調査内容を閲覧できます。
ただし、この調査には「スポーツ国際大会で日本人選手が活躍すること」の調査項目がありません・・・。
東京オリンピック・パラリンピックとスポーツの関わり
趣旨は異なりますが、上述のスポーツ庁の世論調査に面白い調査項目を見つけましたので紹介いたします。
(質問)
「東京オリンピック・パラリンピック」の開催から1年以上が経過しましたが、その後のスポーツとの関わりについて、現在の状況としてあてはまるものを全てお答えください。」
(回答集計:複数選択可)

https://www.mext.go.jp/sports/b_menu/toukei/chousa04/sports/1415963_00008.htm
東京オリンピック・パラリンピックをきっかけにして始めたアクション(スポーツの観戦・応援・スポーツ実施・ボランティア実施)を、調査時点でも継続して行っているか、を質問しています。
継続して行っている人は 26.1%、1/4くらいです。
スポーツ振興の点で、東京オリ・パラは効果があったように見えます。

ただ、この質問は、「東京オリ・パラ観戦以前から行っているアクション」の取り扱いが不明確な感じがします。
もしかすると、東京オリ・パラ観戦以前から行っているアクションを「東京オリ・パラをきっかけにして始めたアクション」に含めて回答した人がいるかもしれません。
たとえば、スポーツの観戦。
次の資料によりますと、この1年間にテレビやインターネットでスポーツ観戦した割合は「72.8%」。
多くの人がスポーツ観戦を行っていることが分かります。
ちなみに観戦人気の高いスポーツは野球、サッカー、マラソン・駅伝です。

ところが、東京オリ・パラをきっかけに興味を持ったスポーツを「現在も観戦している」人は 11.4%。
もちろん、スポーツ観戦習慣が東京オリ・パラをきっかけにしていなければ、この質問にYESと答えないでしょう。
ただ気になるのが、この1年間にスポーツを観戦した人は、次のどちらに反応するでしょう?
・東京オリ・パラを観戦したが今は特に何もしていない/オリ・パラを観戦していない/その他、と答える
・東京オリ・パラの観戦をきっかけに興味を持ったスポーツを現在も観戦している、と答える

そして、スポーツの実施。
世論調査で「週に1日以上スポーツを実施した」と回答した人が 52.4% (過半数)存在します。

赤線は筆者による加筆https://www.mext.go.jp/sports/b_menu/toukei/chousa04/sports/1415963_00008.htm
週1日の頻度でスポーツを実施することは「積極的にスポーツを実施している」と思えます。
こちらはもっと気になります
積極的にスポーツを実施する人は、次のどちらに反応するでしょう?
・東京オリ・パラを観戦したが今は特に何もしていない/オリ・パラを観戦していない/その他、と答える
・東京オリ・パラの観戦をきっかけに観戦したスポーツを現在も実施している、と答える
東京オリ・パラ後もスポーツに関わっているので、太字に反応して、後者の回答をしてしまうかもしれない、こんな印象を受けました(あくまで個人の感想です)。
アンケート調査の質問文章を作成するのはいろいろと難しい、と思った次第です。
(オリ・パラの観戦をきっかけにして実施・観戦するスポーツは無いが、オリ・パラ以前から現在もスポーツを実施/観戦している、のような質問項目があったらよいのでしょうか)

実践する
Pythonで母比率の差の信頼区間の公式を実装します。
Pythonで作成してみよう!
今回は「母比率の差の信頼区間の公式」の実装に取り組みます。
①ライブラリのインポート、関数定義
正規分布近似を前提にした母比率の差の信頼区間を算出する関数を定義します。
母比率の差の信頼区間の公式を実直に書きます。
$${(\hat{p_1}-\hat{p_2}) \pm z_{\alpha/2} \sqrt{\cfrac{\hat{p_1}(1-\hat{p_1})}{n_1}+\cfrac{\hat{p_2}(1-\hat{p_2})}{n_2}}}$$
# インポート
import numpy as np
from scipy.stats import norm
# 母比率の差の信頼区間を算出する関数の定義(正規分布近似)
def proportion_diff_ci(cf, p1, p2, n1, n2):
z_val = norm.isf(q=(1-cf)/2, loc=0, scale=1) # z値
stddev = np.sqrt(p1*(1-p1)/n1+p2*(1-p2)/n2) # 標準偏差の推定値
return (p1-p2) - z_val*stddev, (p1-p2) + z_val*stddev②母比率の差の信頼区間の算出
次のパラメータを設定して、さまざまな比率の差の信頼区間を算出してみましょう!
・信頼係数:cf
・標本比率:p1、p2
・標本サイズ:n1、n2
# 設定 cf:信頼係数、p1,p2:標本比率、n1,n2:標本サイズ
cf = 0.95
p1, n1 = 0.483, 1897
p2, n2 = 0.416, 1925
# 母比率の差の信頼区間の計算
low, high = proportion_diff_ci(cf, p1, p2, n1, n2)
# 信頼区間の表示、検定結果の表示
print(f'母比率の差の{cf*100:.0f}%信頼区間 [{low:.3f}, {high:.3f}]')
if low <= 0 <= high:
print(f'{cf*100:.0f}%信頼区間に0を含むので、'
f'有意水準{(1-cf)*100:.0f}%で両比率に差があると言えない')
else:
print(f'{cf*100:.0f}%信頼区間に0を含まないので、'
f'有意水準{(1-cf)*100:.0f}%で両比率に差があると言える')
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
今回の記事でカテゴリ7「推定の分野」が終わります。
次回からカテゴリ8「検定の分野」が始まります。
今回、検定のさわりを試しています。
帰無仮説、対立仮説、有意水準、検定の種類と利用する分布などに着目すると、統計的仮説検定のイメージが掴みやすいと思います。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?

