
第11章「なんとなく?このブランドが好き」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング2」の第11章「なんとなく?このブランドが好き」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
この章では、携帯キャリア3ブランドのブランド評価モデルをベイズで構築します。
MCMCサンプリングデータをフル活用する「技巧派データ分析」に必死に食らいつきました!

今回の PyMC化 は、まずまずの出来です!
ただしモデルやシミュレーションのロジックが難解でして、理解不能部分が多かったことを告白いたします。
ではでは、PyMCのベイズモデリングの世界を楽しんでまいりましょう!
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 土田尚弘 先生
モデル難易度: ★★★★★ (難しい)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★★★ & GoooD! \\
結果再現度 & ★★★★★ & 最高✨ \\
楽しさ & ★★★★★ & 楽しい! \\
\end{array}
$$

評価ポイント
モデルの構築も、データ分析のための推定量算出やグラフ描画も、私にとってとても難易度が高い章でした。
そんな中で、4回連続でテキストの結果とほぼ一致を迎えることができて、とても嬉しいです!!!Rコードの記述がとても難解な「R技巧派コード」であり、処理内容を読み取れない部分が多くありました。
今回は R Studio でRスクリプトを動かして、アウトプットを確認し、処理内容を推論しました。
工夫・喜び・反省
「図11.1」のブランド別予測分布の描画には難儀しました。図11.1を描画するRスクリプトを見つけることができす、どうやったら目的変数$${y}$$の予測分布を算出できるのか、途方に暮れる状況でした。
日を開けてテキストの説明変数の記述をよく読むと、グラフの1本の曲線が説明変数1ケースで作成できることに気づけて、なんとか図を描画できました。
「寝かせる」のって大切ですね !

モデルの概要
テキストの調査・実験の概要
■ 調査の概要
この章は、ドコモ、au、ソフトバンクの3つの携帯キャリアのブランド評価を取り扱っています。
2019年3月3日から2019年3月5日に実施されたWeb調査で「3ブランドの認知者」から収集した延べ1479サンプルデータを分析に使用しています。
■ 調査の関心ごと
評価対象ブランドの「利用経験の有無」や「CM視聴経験の有無」が個人の「ブランド評価」にどのように影響するかに先生は思いをめぐらせます。
人によって経験が異なる場合、さらにその経験の評価によってブランドの評価が変わる場合に、どのように分析すればよいのか?そして経験によって、何か違いがあるのか?
調査データに含まれる、以下の3つの調査項目を軸にして、ベイズモデリングによる分析が始まります。
1.ブランド評価(全員)
「ブランドの好意度を示す評価」であり、非常に嫌い~どちらともいえない~非常に好きの7段階尺度で調査
2.利用満足度(該当者のみ)
現在のブランド利用者限定で利用満足度を「非常に不満~どちらともいえない~非常に満足」の7段階尺度で調査
3.CM評価(該当者のみ)
直近3か月にブランドのCM広告(媒体問わない)を見た人限定でCM広告の好意度を「非常に嫌い~どちらともいえない~非常に好き」の7段階尺度で調査
なお、7段階尺度は、-3~0~3の値に変換されます。

■ 分析テーマ
テキストは以下の4つの分析テーマに焦点を当てて議論を進めます。
頭の片隅においておくと、以降の記事が読みやすくなるかと思います。
1.CMを見ていない、どちらともいえないの差(11.5.1項)
調査データには、CMを見ていない人のブランド評価とCMを見た人のブランド評価が混在しています。
CMを見た人の場合には「CM評価」と「ブランド評価」の関係を探ることができます。
例えばCMが好評価の場合、ブランド評価が高くなるか、などです。
しかし、CMを見ていない人の場合には「CM評価」が無いため「CM評価」と「ブランド評価」の関係を探ることが難しいです。
CMを見ていない場合、CM評価尺度の中で中立的な「どちらともいえない」を割り当てるのが簡単な方法かもしれない、とテキストは記載しています。
ただし、CMを見てない場合と、CMを見ていてCM評価を「どちらともいえない」と回答する場合とを「本当に同等としてみなしてよいのか疑問が残る」ともテキストは記載しています。
そこで、ベイズの予測分布を活用して、CMを見ていない場合とどちらともいえないの差を検討します。
2.CMを見ていない場合と見た場合のブランド評価のバラツキの比較(11.5.2項)
テキストではモデリングの際、モデルの分散構造に「ブランド利用」と「CM認知」の経験の有無を考慮しています。
そこで、ベイズの事後分布を活用して、CMを見ていない場合と見た場合のバラツキの違いを検討します。
3.もしドコモのCM評価がauと同一だったら?(11.5.3項)
ドコモはブランド評価はトップですが、CM評価はauよりも低いです。
そこで、ベイズの予測分布を活用して、もしもドコモのCM評価がauと同等だったら・・と仮定してブランド評価を推論(シミュレーション)します。
4.auがドコモのシェアを奪っていったら?(11.5.4項)
調査ではドコモがトップシェアです。
利用者が多いほうがブランド評価が高いとする仮説のもとで、もしもauがドコモのシェアを奪っていったらブランド評価にどのように影響するのか、をベイズの事後分布を活用して推論(シミュレーション)します。

■ 調査データの構造
テキストの表11.1を参考にして、データ項目説明表を作成しました。
モデル数式への橋渡し(はしやすめ?)にいかがでしょう。
クリック(タップ)すると拡大できます。

テキストのモデリング
■ 目的変数と関心のあるパラメータ
目的変数は主に「ブランド評価$${y^{(j)}_i}$$」です。
添字$${i}$$は調査対象者ID、$${j}$$はブランドです。
関心のあるパラメータや統計量は分析テーマごとに明らかになります。
■ モデル数式
11.5.1項の分析に用いるモデルです。
こちらは線形重回帰モデルです。
$$
\begin{align*}
&y^{(j)}_i = \beta_{0j} + \beta_1 d^{(j)}_{i1} + \beta_2 d^{(j)}_{i2} + \beta_3d^{(j)}_{i1}z^{(j)}_{i1} + \beta_4d^{(j)}_{i2}z^{(j)}_{i2} + \varepsilon^{(j)}_i \\
&\varepsilon^{(j)}_i \sim \text{Normal}\ (0,\ \sigma^2_{(j)i}) \\
&\log \left(\sigma^2_{(j)i} \right) = \gamma_{0j} + \gamma_1 d^{(j)}_{i1} + \gamma_2d^{(j)}_{i2} \\
\\
&\beta_{01},\beta_{02},\beta_{03},\beta_{1},\beta_{2},\beta_{3},\beta_{4} \sim \text{Normal}\ (0,\ 100) \\
&\gamma_{01},\gamma_{02},\gamma_{03},\gamma_{1},\gamma_{2} \sim \text{Normal}\ (0,\ 100) \\
\end{align*}
$$
テキストでは、1行目の重回帰の係数にあたるパラメータ$${\beta}$$を「平均構造に関するパラメータ」と呼んでいます。
また、3行目の数式で表される分散構造には「対数線形モデル」を用いており、(おそらくこちらも重回帰の)係数にあたるパラメータ$${\gamma}$$を「分散構造に関するパラメータ」と呼んでいます。

続いて11.5.2項以降の分析に用いるモデルです。
説明変数$${d^{(j)}_{i1}, d^{(j)}_{i2}, z^{(j)}_{i1}, z^{(j)}_{i2}}$$が尤度関数の左辺(観測値)に現れています。
$$
\begin{align*}
&d^{(j)}_{i1} \sim \text{Bernoulli}\ (p^{(j)}_1) \\
&d^{(j)}_{i2} \sim \text{Bernoulli}\ (p^{(j)}_2) \\
\\
&z^{(j)}_{i1} \sim \text{Normal}\ (\mu^{(j)}_1,\ s^2_{(j)1}), \text{if}\ d^{(j)}_{i1}=1\ \text{and}\ d^{(j)}_{i2}=0 \\
&z^{(j)}_{i2} \sim \text{Normal}\ (\mu^{(j)}_2,\ s^2_{(j)2}), \text{if}\ d^{(j)}_{i1}=0\ \text{and}\ d^{(j)}_{i2}=1 \\
&\boldsymbol{z_i}^{(j)} = \left(z^{(j)}_{i2},\ z^{(j)}_{i2} \right)^{\top} \sim \text{MvNormal}\ (\boldsymbol{m}^{(j)},\ \boldsymbol{V}^{(j)}), \text{if}\ d^{(j)}_{i1}=1\ \text{and}\ d^{(j)}_{i2}=1 \\
\\
&p^{(j)}_1, p^{(j)}_2 \sim \text{beta}\ (1,\ 1) \\
&\mu^{(j)}_1, \mu^{(j)}_2 \sim \text{Normal}\ (0,\ 100^2) \\
&s^2_{(j)1}, s^2_{(j)2} \sim \text{HalfCauchy}\ (2.5) \\
&\boldsymbol{m}^{(j)} \sim \text{Normal}\ (\boldsymbol{0},\ 100^2 \boldsymbol{I}_2) \\
&\boldsymbol{V}^{(j)}は省略 \\
\end{align*}
$$
また、11.5.3項および11.5.4項の分析に用いる数式があります。
ぜひテキストにてご確認ください。
私の理解の限界を超えました(空)

■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルの推論値を利用した分析は「PyMC実装」章をご覧ください。
PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
import scipy.stats as stats
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込み
csvファイルをpandasのデータフレームに読み込みます。
列名を日本語単語に変更し、IDが文字型になるように設定しました。
### データの読み込み
# 列名の定義
names = ['ID', 'ブランド評価', 'ドコモ', 'au', 'ソフトバンク', 'ブランド利用',
'CM認知', '満足度', 'CM評価']
# データの読み込み dtype:最初の列IDを文字列に設定する
data = pd.read_csv('chapter11Data.csv', dtype={0: str}, header=0, index_col=0,
names=names)
display(data)【実行結果】

3.データの概観の確認
テキスト表11.2の記述統計を算出します。
まずは記述統計算出関数の定義から。
### 要約統計量算出関数の定義
def calc_stats1(col):
## 引数colで指定したキャリアを抽出して一時データフレームを作成
tmp = data[data[col]==1]
## 統計量の算出
# 標本サイズの算出
n = len(tmp)
# ブランド評価の平均と標準偏差の算出
brand_rate_mean = tmp['ブランド評価'].mean()
brand_rate_std = tmp['ブランド評価'].std(ddof=0)
# 利用者数と利用率(%)の算出
user_num = tmp['ブランド利用'].sum()
user_share = tmp['ブランド利用'].mean() * 100
# 満足度の平均と標準偏差の算出
satisfy_rate_mean = tmp[tmp['ブランド利用']==1]['満足度'].mean()
satisfy_rate_std = tmp[tmp['ブランド利用']==1]['満足度'].std(ddof=0)
# CM視聴者数と視聴率(%)の算出
cm_view_num = tmp['CM認知'].sum()
cm_view_share = tmp['CM認知'].mean() * 100
# CM評価の平均と標準偏差の算出
cm_rate_mean = tmp[tmp['CM認知']==1]['CM評価'].mean()
cm_rate_std = tmp[tmp['CM認知']==1]['CM評価'].std(ddof=0)
## 戻り値:算出した全統計量
return n, brand_rate_mean, brand_rate_std, user_num, user_share,\
satisfy_rate_mean, satisfy_rate_std, cm_view_num, cm_view_share,\
cm_rate_mean, cm_rate_std記述統計量を算出します。
### キャリアのブランド評価データの記述統計の表示 ※表11.2に相当
# 統計量の項目リスト
cols = ['標本サイズ', 'ブランド評価平均', '(標準偏差)', '利用者数', '(%)',
'満足度平均', '(標準偏差)', 'CM認知者数', '(%)', 'CM評価平均', '(標準偏差)']
# ブランド名のリスト
brand = ['ドコモ', 'au', 'ソフトバンク']
# データフレーム形式で記述統計を表示
stats_df1 = pd.DataFrame({brand[0]: calc_stats1(brand[0]),
brand[1]: calc_stats1(brand[1]),
brand[2]: calc_stats1(brand[2])},
index=cols).round(3)
display(stats_df1)【実行結果】
かっこ表記の標準偏差$${sd}$$や$${\%}$$は別行にしました。


モデル前半の構築 11.5.1項の分析用
11.5.1項では、ブランド非利用者について、CMを見ていないケース vs CMを見ていてCM評価を「どちらともいえない」と回答したケース のブランド評価の比較を実施します。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$${\beta}$$の形状は説明変数$${X}$$の要素数$${meanParam=7}$$、$${\gamma}$$の形状は説明変数$${H}$$の要素数$${varParam=5}$$です。
また数式中の記号$${@}$$は行列の積(ドット積)を示します。
$$
\begin{align*}
\beta &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=100,\ \text{dims}=meanParam) \\
\gamma &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=100,\ \text{dims}=varParam) \\
likelihood &\sim \text{Normal}\ (\text{mu}=X @ \beta,\ \text{sigma}=\text{sqrt}(\exp(H @ \gamma)),\ \text{dims}=data) \\
\end{align*}
$$

1.モデルの定義
数式表現を実直にモデル記述します。
### モデルの定義
with pm.Model() as model:
## coordの定義
model.add_coord('data', values=data.index, mutable=True)
model.add_coord('meanParam', values=['01', '02', '03', '1', '2', '3', '4']
, mutable=True)
model.add_coord('varParam', values=['01', '02', '03', '1', '2']
, mutable=True)
## dataの定義
# ブランド評価
y = pm.ConstantData('y', value=data['ブランド評価'].values, dims='data')
# 平均構造の説明変数
X = pm.ConstantData('X', value=data.iloc[:, 1:].values,
dims=('data', 'meanParam'))
# 分散構造の説明変数
H = pm.ConstantData('H', value=data.iloc[:, 1:6].values,
dims=('data', 'varParam'))
## 事前分布
# 平均構造の係数
beta = pm.Normal('beta', mu=0, sigma=100, dims='meanParam')
# 分散構造の係数
gamma = pm.Normal('gamma', mu=0, sigma=100, dims='varParam')
## 尤度
likelihood = pm.Normal('likelihood', observed=y,
mu=X @ beta, sigma=pt.sqrt(pt.exp(H @ gamma)),
dims='data')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の3つを設定しました。データの行の座標:名前「data」、値「行インデックス」
平均構造のパラメータの座標:名前「meanParam」、値「平均構造のパラメータの添字」
分散構造のパラメータの座標:名前「varParam」、値「分散構造のパラメータの添字」
dataの定義
次の3つを設定しました。ブランド評価:Y (目的変数)
平均構造の説明変数:X(データのドコモ~CM評価の値)
分散構造の説明変数:H(データのドコモ~CM認知の値)
パラメータの事前分布
モデルの数式表現のとおりです。
尤度
平均パラメータが線形予測子、標準偏差パラメータが対数線形モデルの正規分布です。
2.モデルの外観の確認
# モデルの表示
model【実行結果】
とてもシンプルなモデルです

### モデルの可視化
pm.model_to_graphviz(model)【実行結果】


3.事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ1分10秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 1分10秒
# テキスト: iter=11000, warmup=1000, chains=4
with model:
idata = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R} > 1.01}$$のパラメータは0件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
テキストの表11.3の代用です。なお、テキストは信用区間を表示していますが、このコードではHDI区間を表示しています。
### 推論データの要約統計情報の表示 ※表11.3に相当 (ただしHDI区間を表示)
pm.summary(idata, hdi_prob=0.95, round_to=3)【実行結果】
各パラメータの事後平均および標準偏差はテキストとほぼ同じ結果になりました。

トレースプロットで事後分布サンプリングデータの様子を確認します。
### トレースプロットの表示
pm.plot_trace(idata, compact=True)
plt.tight_layout();【実行結果】
左のグラフから、4本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

5.推論データの保存
推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idata をpickleで保存します。
### idataの保存 pickle
file = r'idata_ch11.pkl'
with open(file, 'wb') as f:
pickle.dump(idata, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_ch11.pkl'
with open(file, 'rb') as f:
idata_load = pickle.load(f)
モデル後半の構築 11.5.2項以降の分析用
11.5.2項以降に用いるモデルを構築します。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
Stanコードから私の実装可能レベル(低次元)に変換してみました。
(ただし、数式の意味は難解で理解できていません・・・)
$$
\begin{align*}
P &\sim \text{Beta}\ (\text{alpha}=1,\ \text{beta}=1,\ \text{dims}=(brand,\ rating)) \\
\mu_1 &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=100,\ \text{dims}=(brand,\ rating)) \\
\sigma_1 &\sim \text{HalfCauchy}\ (\text{beta}=2.5,\ \text{dims}=(brand,\ rating)) \\
\mu_2 &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=100,\ \text{dims}=(brand,\ rating)) \\
\\
sd\_dist0 &\sim \text{HalfCauchy}\ (\text{beta}=2.5,\ \text{shape}=2) \\
chol0 &= \text{LKJCholeskyCov}\ (\text{eta}=1,\ \text{n}=2,\ \text{sd\_dist}=sd\_dist0) \\
cov0 &= chol0 @ chol0^{\top},\ \text{dims}=(rathing,\ rating2) \\
\\
sd\_dist1 &\sim \text{HalfCauchy}\ (\text{beta}=2.5,\ \text{shape}=2) \\
chol1 &= \text{LKJCholeskyCov}\ (\text{eta}=1,\ \text{n}=2,\ \text{sd\_dist}=sd\_dist1) \\
cov1 &= chol1 @ chol1^{\top},\ \text{dims}=(rathing,\ rating2) \\
\\
sd\_dist2 &\sim \text{HalfCauchy}\ (\text{beta}=2.5,\ \text{shape}=2) \\
chol2 &= \text{LKJCholeskyCov}\ (\text{eta}=1,\ \text{n}=2,\ \text{sd\_dist}=sd\_dist2) \\
cov2 &= chol2 @ chol2^{\top},\ \text{dims}=(rathing,\ rating2) \\
\\
likeliD1 &\sim \text{Bernoulli}\ (\text{p}=P[brandidx,\ 0]),\ \text{dims}=data) \\
likeliD2 &\sim \text{Bernoulli}\ (\text{p}=P[brandidx,\ 1]),\ \text{dims}=data) \\
likeliZ1 &\sim \text{Normal}\ (\text{mu}=\mu_1[brandidxZ1,\ 0],\ \text{sigma}=\sqrt{\sigma_1[brandIdxZ1,\ 0]}),\ \text{dims}=dataZ1) \\
likeliZ2 &\sim \text{Normal}\ (\text{mu}=\mu_1[brandidxZ2,\ 1],\ \text{sigma}=\sqrt{\sigma_1[brandIdxZ2,\ 1]}),\ \text{dims}=dataZ2) \\
likeliZ12d &\sim \text{MvNormal}\ (\text{mu}=\mu_2[0,\ :],\ \text{cov}=cov0),\ \text{dims}=(dataZ12d,\ rating)) \\
likeliZ12a &\sim \text{MvNormal}\ (\text{mu}=\mu_2[1,\ :],\ \text{cov}=cov1),\ \text{dims}=(dataZ12a,\ rating)) \\
likeliZ12s &\sim \text{MvNormal}\ (\text{mu}=\mu_2[2,\ :],\ \text{cov}=cov2),\ \text{dims}=(dataZ12s,\ rating)) \\
\end{align*}
$$

1.モデルの定義
数式表現を実直にモデル記述します。
また、モデル定義に先立って、データの前処理を行います。
### データの前処理
# ブランド列を追加
data_mod = data.copy()
data_mod['ブランド'] = data_mod.apply(lambda x: 0 if x['ドコモ']==1
else 1 if x['au']==1
else 2, axis=1)
# 目的変数z1(ブランド利用あり・CM未認知)のみのデータの作成
data_z1 = (data_mod.query('ブランド利用==1 & CM認知==0')[['ブランド', '満足度']]
.reset_index())
# 目的変数z2(ブランド利用なし・CM認知)のみのデータの作成
data_z2 = (data_mod.query('ブランド利用==0 & CM認知==1')[['ブランド', 'CM評価']]
.reset_index())
# 目的変数z12ドコモ(ブランド利用あり・CM認知)のみのデータの作成
data_z12d = (data_mod.query('ブランド利用==1 & CM認知==1 & ブランド==0')
[['満足度', 'CM評価']].reset_index())
# 目的変数z12au(ブランド利用あり・CM認知)のみのデータの作成
data_z12a = (data_mod.query('ブランド利用==1 & CM認知==1 & ブランド==1')
[['満足度', 'CM評価']].reset_index())
# 目的変数z12ソフトバンク(ブランド利用あり・CM認知)のみのデータの作成
data_z12s = (data_mod.query('ブランド利用==1 & CM認知==1 & ブランド==2')
[['満足度', 'CM評価']].reset_index())モデルの定義に入ります。
尤度関数がめっちゃ多いのが特徴!
### モデルの定義
with pm.Model() as model2:
### データ関連定義
## coordの定義
# 各データのインデックス
model2.add_coord('data', values=data.index, mutable=True)
model2.add_coord('dataZ1', values=data_z1.index, mutable=True)
model2.add_coord('dataZ2', values=data_z2.index, mutable=True)
model2.add_coord('dataZ12d', values=data_z12d.index, mutable=True)
model2.add_coord('dataZ12a', values=data_z12a.index, mutable=True)
model2.add_coord('dataZ12s', values=data_z12s.index, mutable=True)
# ブランド3種
model2.add_coord('brand', values=brand, mutable=True)
# 評価項目2種
model2.add_coord('rating', values=['満足度', 'CM評価'], mutable=True)
model2.add_coord('rating2', values=['満足度', 'CM評価'], mutable=True)
## dataの定義
# ブランド利用データ
d1 = pm.ConstantData('d1', value=data_mod['ブランド利用'].values, dims='data')
# CM認知データ
d2 = pm.ConstantData('d2', value=data_mod['CM認知'].values, dims='data')
# ブランドインデックス
brandIdx = pm.ConstantData('brandIdx', value=data_mod['ブランド'].values,
dims='data')
# z1,z2,z12d,z12a,z12aデータ
z1 = pm.ConstantData('z1', value=data_z1['満足度'].values, dims='dataZ1')
z2 = pm.ConstantData('z2', value=data_z2['CM評価'].values, dims='dataZ2')
z12d = pm.ConstantData('z12d', value=data_z12d[['満足度', 'CM評価']].values,
dims=('dataZ12d', 'rating'))
z12a = pm.ConstantData('z12a', value=data_z12a[['満足度', 'CM評価']].values,
dims=('dataZ12a', 'rating'))
z12s = pm.ConstantData('z12s', value=data_z12s[['満足度', 'CM評価']].values,
dims=('dataZ12s', 'rating'))
# z1,z2用のブランドインデックス
brandIdxZ1 = pm.ConstantData('brandIdxZ1', value=data_z1['ブランド'].values,
dims='dataZ1')
brandIdxZ2 = pm.ConstantData('brandIdxZ2', value=data_z2['ブランド'].values,
dims='dataZ2')
### 事前分布
# ベルヌーイ分布の確率
P = pm.Beta('P', alpha=1, beta=1, dims=('brand', 'rating'))
# z1, z2用の1変量正規分布の平均
mu1 = pm.Normal('mu1', mu=0, sigma=100, dims=('brand', 'rating'))
# z1, z2用の1変量正規分布の分散
sigma1 = pm.HalfCauchy('sigma1', beta=2.5, dims=('brand', 'rating'))
# z12用の2変量正規分布の平均
mu2 = pm.Normal('mu2', mu=0, sigma=100, dims=('brand', 'rating'))
## z12用の2変量正規分布の分散共分散行列(ブランド別に作成)
# ドコモ用
sd_dist0 = pm.HalfCauchy.dist(beta=2.5, shape=2)
chol0, _, _ = pm.LKJCholeskyCov('chol0', eta=1, n=2, sd_dist=sd_dist0)
cov0 = pm.Deterministic('cov0', chol0 @ chol0.T, dims=('rating', 'rating2'))
# au用
sd_dist1 = pm.HalfCauchy.dist(beta=2.5, shape=2)
chol1, _, _ = pm.LKJCholeskyCov('chol1', eta=1, n=2, sd_dist=sd_dist1)
cov1 = pm.Deterministic('cov1', chol1 @ chol1.T, dims=('rating', 'rating2'))
# ソフトバンク用
sd_dist2 = pm.HalfCauchy.dist(beta=2.5, shape=2)
chol2, _, _ = pm.LKJCholeskyCov('chol2', eta=1, n=2, sd_dist=sd_dist2)
cov2 = pm.Deterministic('cov2', chol2 @ chol2.T, dims=('rating', 'rating2'))
# 3ブランドの分散共分散行列を1まとめにする
covs = pm.Deterministic('covs', pt.stack([cov0, cov1, cov2]),
dims=('brand', 'rating', 'rating2'))
### 尤度
# d1:利用有無
likeliD1 = pm.Bernoulli('likeliD1', p=P[brandIdx, 0], observed=d1,
dims='data')
# d2:CM認知有無
likeliD2 = pm.Bernoulli('likeliD2', p=P[brandIdx, 1], observed=d2,
dims='data')
# z1:利用あり・CM未認知のケースのブランド評価
likeliZ1 = pm.Normal('likeliZ1', mu=mu1[brandIdxZ1, 0],
sigma=pt.sqrt(sigma1[brandIdxZ1, 0]),
observed=z1, dims='dataZ1')
# z2:利用なし・CM認知のケースのCM評価
likeliZ2 = pm.Normal('likeliZ2', mu=mu1[brandIdxZ2, 1],
sigma=pt.sqrt(sigma1[brandIdxZ2, 1]),
observed=z2, dims='dataZ2')
# z12docomo:利用あり・CM認知・ドコモのケースのブランド評価とCM評価
likeliZ12d = pm.MvNormal('likeliZ12d', mu=mu2[0, :], cov=cov0, observed=z12d,
dims=('dataZ12d', 'rating'))
# z12au:利用あり・CM認知・auのケースのブランド評価とCM評価
likeliZ12a = pm.MvNormal('likeliZ12a', mu=mu2[1, :], cov=cov1, observed=z12a,
dims=('dataZ12a', 'rating'))
# z12softbank:利用あり・CM認知・ソフトバンクのケースのブランド評価とCM評価
likeliZ12s = pm.MvNormal('likeliZ12s', mu=mu2[2, :], cov=cov2, observed=z12s,
dims=('dataZ12s', 'rating'))【モデル注釈】省略:複雑すぎて説明不能なのです・・・
2.モデルの外観の確認
LKJCholeskyCovを用いたことで変数名に「_」(アンダースコア)が含まれたので、いつもと異なる方法で確率変数の数式を見てみます。
# モデルの表示
model2.basic_RVs【実行結果】

### モデルの可視化
pm.model_to_graphviz(model2)【実行結果】
かなり複雑なモデルです。
多変量正規分布 $${\text{MvNormal}}$$は複雑ですね・・・


3.事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ50秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 50秒
# テキスト: iter=11000, warmup=1000, chains=4
with model2:
idata2 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata2 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
(az.rhat(idata_in) > threshold).sum()【実行結果】
$${\hat{R} > 1.01}$$のパラメータは0件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata2, hdi_prob=0.95, round_to=3)【実行結果】

トレースプロットで事後分布サンプリングデータの様子を確認します。
パラメータの一部のみを表示しています。
### トレースプロットの表示
pm.plot_trace(idata2, compact=False)
plt.tight_layout();【実行結果】
左のグラフから、4本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

5.推論データの保存
推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idata2 をpickleで保存します。
### idataの保存 pickle
file = r'idata2_ch11.pkl'
with open(file, 'wb') as f:
pickle.dump(idata2, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata2_ch11.pkl'
with open(file, 'rb') as f:
idata2_load = pickle.load(f)
分析~テキストにならって
【分析1】11.5.1 CMを見ていない、どちらともいえないの差
ブランド非利用者を対象にして、CMを見ていないグループと、CMを見ていてCM評価を「どちらともいえない」と答えたグループの「ブランド評価」の比較をします。
テキストの図11.1のグラフを描画します。
目的変数である「ブランド評価」の予測分布を算出してKDEをプロットします。
この章で最も難儀したコードです。「yの予測に用いる説明変数Xの設定」に気づくのにかなり時間を食ってしまいました。
### ブランド別の(a)と(b)の予測分布の描画 ※図11.1に相当
## 初期値設定
# 乱数シードの設定
np.random.seed(1234)
## yの予測に用いる説明変数Xの設定 (説明変数HはXの先頭5要素)
# ドコモ・ブランド利用なし・CM認知なし
d_val_non = np.array([1, 0, 0, 0, 0, 0, 0])
# ドコモ・ブランド利用なし・CM認知あり・どちらとも言えない
d_val_see = np.array([1, 0, 0, 0, 1, 0, 0])
# au・ブランド利用なし・CM認知なし
a_val_non = np.array([0, 1, 0, 0, 0, 0, 0])
# au・ブランド利用なし・CM認知あり・どちらとも言えない
a_val_see = np.array([0, 1, 0, 0, 1, 0, 0])
# ソフトバンク・ブランド利用なし・CM認知なし
s_val_non = np.array([0, 1, 0, 0, 0, 0, 0])
# ソフトバンク・ブランド利用なし・CM認知あり・どちらとも言えない
s_val_see = np.array([0, 1, 0, 0, 1, 0, 0])
## 描画用データの作成
# 推論データからパラメータβ,γのサンプリングデータを取り出し
beta_samples = idata.posterior.beta.stack(sample=('chain', 'draw')).T.data
gamma_samples = idata.posterior.gamma.stack(sample=('chain', 'draw')).T.data
# yの予測関数の定義 (stats.normで正規分布乱数を生成)
def pred_y(val):
return np.array([stats.norm.rvs(loc=val @ b_sample,
scale=np.sqrt(np.exp(val[:5] @ g_sample)))
for (b_sample, g_sample)
in zip(beta_samples, gamma_samples)])
# yの予測分布の算出 (上述の説明変数Xを利用)
d_non_cm = pred_y(d_val_non) # ドコモ, CMを見ていない
d_see_cm = pred_y(d_val_see) # ドコモ, CM評価「どちらでもない」と回答
a_non_cm = pred_y(a_val_non) # au, CMを見ていない
a_see_cm = pred_y(a_val_see) # au, CM評価「どちらでもない」と回答
s_non_cm = pred_y(s_val_non) # ソフトバンク, CMを見ていない
s_see_cm = pred_y(s_val_see) # ソフトバンク, CM評価「どちらでもない」と回答
# yの予測分布データをリスト化
non_cm_list = [d_non_cm, a_non_cm, s_non_cm]
see_cm_list = [d_see_cm, a_see_cm, s_see_cm]
## 描画処理
# 描画領域の設定
fig, ax = plt.subplots(1, 3, figsize=(12, 4), sharex=True, sharey=True)
# ブランドごとに描画を繰り返し処理
for i, (non_cm, see_cm, brandname) in enumerate(zip(non_cm_list,
see_cm_list, brand)):
## KDEプロットの描画処理
# KDEプロットの描画(CM見ていない、CM評価あり)
kde_plot_non = sns.kdeplot(x=non_cm, ax=ax[i], color='tab:blue')
kde_plot_see = sns.kdeplot(x=see_cm, ax=ax[i], color='tomato', ls='--')
## 最頻値=MAP推定値の算出
# KDEプロットで描画した線から、x軸,y軸の全値を取得
kde_data_non = kde_plot_non.get_lines()[0].get_data()
kde_data_see = kde_plot_see.get_lines()[1].get_data()
# KDEプロットのyの最大値(最頻値)のインデックスを取得
kde_max_idx_non = kde_data_non[1].argmax()
kde_max_idx_see = kde_data_see[1].argmax()
# KDEプロットのyの最大値≒MAP推定値の垂直線の描画
ax[i].vlines(x=kde_data_non[0][kde_max_idx_non], ymin=0,
ymax=kde_data_non[1][kde_max_idx_non], color='tab:blue')
ax[i].vlines(x=kde_data_see[0][kde_max_idx_see], ymin=0,
ymax=kde_data_see[1][kde_max_idx_see], color='tomato', ls='--')
## 修飾
ax[i].set(title=brandname, xlabel=f'$y_i^{{({i+1})}}$', ylim=(0, 0.5))
ax[i].grid(lw=0.3)
fig.legend(labels=['CMを見ていない', 'CM評価「どちらともいえない」'],
loc='lower center', bbox_to_anchor=(0.5, 1), ncol=2, fontsize=14)
plt.tight_layout();【実行結果】
テキストに近い結果になりました。

【分析】~テキストにならって
赤い点線のCM評価「どちらともいえない」と答えたグループの方が、全ブランドともに、ブランド評価の平均値が大きく、分散が小さいです。
CMを見ていない場合と、CMを見た結果「CMは良いとも悪いともいえない」と答えた場合では、明らかな違いがありそうです。
続いてテキストの表11.4の効果量・非重複度・優越率の算出を行います。
CMを見ていないグループとCM評価「どちらともいえない」グループの違いを定量化します。
### CMを見ていない場合とCMを見たけどCM評価が「どちらとも言えない」場合の差
# ※表11.4に相当
# 推論データからパラメータβとγのサンプリングデータを取り出し
betas = idata.posterior.beta.stack(sample=('chain', 'draw')).data
gammas = idata.posterior.gamma.stack(sample=('chain', 'draw')).data
# 初期値設定 m:ブランド数(3)、b2:β2・γ2の取り出しに使うindex
m = len(brand)
b2 = m - 1 + 2
stats_df2 = pd.DataFrame()
## ブランドごとに統計量を算出してデータフレームに格納する処理を繰り返す
for j, brandname in enumerate(brand):
## 統計量の算出
# 効果量1=β2 / sqrt(exp(γj))
es1 = betas[b2] / np.sqrt(np.exp(gammas[j]))
# 効果量2=β2 / sqrt(exp(γj+γ1))
es2 = betas[b2] / np.sqrt(np.exp(gammas[j] + gammas[b2]))
# 非重複度1=正規分布の累積分布関数(x=βj+β2, mu=βj, sigma=sqrt(exp(γj)))
no1 = stats.norm.cdf(x=betas[j]+betas[b2], loc=betas[j],
scale=np.sqrt(np.exp(gammas[j])))
# 非重複度2=1-正規分布の累積分布関数(x=βj, mu=βj+β2, sigma=sqrt(exp(γj+γ2)))
no2 = 1- stats.norm.cdf(x=betas[j], loc=betas[j]+betas[b2],
scale=np.sqrt(np.exp(gammas[j]+gammas[b2])))
# 優越率=正規分布の累積分布関数(x=β2/sqrt(exp(γj)+exp(γj+γ2)), mu=0, sigma=1)
pd1 = stats.norm.cdf(
x=betas[b2] / np.sqrt(np.exp(gammas[j])
+ np.exp(gammas[j] + gammas[b2])),
loc=0, scale=1)
## データフレームに結合
# 統計量(平均)をstats_df2に結合
tmp_df = pd.DataFrame(
[es1.mean(), es2.mean(), no1.mean(), no2.mean(), pd1.mean()],
columns=pd.MultiIndex.from_tuples([(brandname, '平均')]))
stats_df2 = pd.concat([stats_df2, tmp_df], axis=1)
# 統計量(標準偏差)をstats_df2に結合
tmp_df = pd.DataFrame(
[es1.std(), es2.std(),no1.std(), no2.std(), pd1.std()],
columns=pd.MultiIndex.from_tuples([(brandname, '標準偏差')]))
stats_df2 = pd.concat([stats_df2, tmp_df], axis=1)
# データフレームのインデックスの整理
stats_df2.index = ['効果量1', '効果量2', '非重複度1', '非重複度2', '優越率']
# 完成したデータフレームの表示
stats_df2.round(3)【実行結果】
テキストに近い値になったと思います。

【分析】~テキストにならって
効果量は標準化した差を示していて、10倍すると偏差値的に扱えるそうです。この表からは2つのグループには偏差値3~5程度の差があるといえるそうです。
非重複度は平均から比較グループの代表的な人の分位点を示すそうで、0.6超です。
優越率はCM評価「どちらともいえない」グループのブランド評価が高い確率を示すそうで、6割を超えています。
これらの値は「差がある」「違いがある」ことを示しており、CM評価「どちらともいえない」グループのほうがブランド評価を高く回答していると想定されます。
テキストは「CMを見ていないことと、どちらともいえないということは、根本的に異なることは間違いなくいえるだろう」と締めくくっています。

【分析2】11.5.2 CMを見ていない場合と見た場合のブランド評価のバラツキ比較
この項では、ブランド非利用者を対象にして、CMを見ていないグループと、CMを見たグループのブランド評価の分散比を分析します。
見ていないグループの分散を分子、見たグループの分散を分母にし、分散比が1以上なら、ブランドを使っておらず、CMも見ていない人のほうがブランドに対して評価のバラツキがあると言えるそうです。
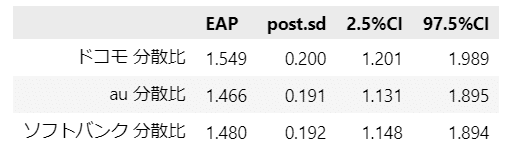
テキスト表11.5の分散比の事後平均と95%信用区間を算出します。
### cとdの分散比の事後平均と95%信用区間の算出 ※表11.5に相当
## 事後統計量算出関数の定義
def calc_stats2(x):
ci = np.quantile(x, q=[0.025, 0.975])
return np.mean(x), np.std(x), ci[0], ci[1]
## データの準備
# 推論データから標準偏差の取り出し
sigma1s = idata2.posterior.sigma1.stack(sample=('chain', 'draw')).data
# 初期値設定
sigmas_ratio = []
stats_df3 = pd.DataFrame()
b4 = 6 # β4 :βパラメータの6番目の値を指定
g2 = 4 # γ2 :γパラメータの4番目の値を指定
## ブランドごとに事後統計量の算出を繰り返し処理
for j in range(m):
# ケースc「CMを見ていない人」分散の算出 shape=(4000)
sigma_jc = np.exp(gammas[j])
# ケースd「CMを見ている人」の分散」算出 shape=(4000)
sigma_jd = betas[b4]**2*sigma1s[j, 1, :] + np.exp(gammas[j] + gammas[g2])
# 分散比の算出 shape=(4000)
sigma_jc_div_jd = sigma_jc / sigma_jd
# 描画用のデータ格納
sigmas_ratio.append(sigma_jc_div_jd)
# 事後統計量を算出してデータフレームに結合
tmp = pd.DataFrame(calc_stats2(sigma_jc_div_jd),
columns=[f'{brand[j]} 分散比'])
stats_df3 = pd.concat([stats_df3, tmp], axis=1)
## データフレームの最終化
# データフレームの列名をセット
stats_df3 = stats_df3.T.set_axis(labels=['EAP', 'post.sd', '2.5%CI', '97.5%CI'],
axis=1)
# データフレームの表示
display(stats_df3.round(3))【実行結果】
テキストの結果に近いと思います。3ブランドとも95%信用区間は1を超えています。
テキスト図11.2の分散比の事後分布を描画します。
### CMを見ていない場合と見ている場合の分散比の事後分布の描画 ※図11.2に相当
# 描画領域の指定
fig, ax = plt.subplots(1, 3, figsize=(10, 3), sharey=True)
# ブランドごとに描画を繰り返し処理
for i, brandname in enumerate(brand):
# KDEの描画
pm.plot_dist(sigmas_ratio[i], ax=ax[i])
# 修飾
ax[i].set(xlim=(0.5, 2.5), xticks=[0.5, 1, 1.5, 2, 2.5], ylim=(0, 2.5),
title=brandname)
ax[i].grid(lw=0.5)
plt.tight_layout();【実行結果】
3ブランドのすべてが分散比ほぼ1以上、というように読めます。

分散比が1未満になる確率を算出します。
### cとdの分散比が1未満の確率の算出 ※テキスト127ページの分散比1未満の確率
brand_eng = ['docomo', 'au', 'softbank']
for j in range(len(brand)):
val = (sigmas_ratio[j] < 1).mean()
print(f'{brand_eng[j]:>8}: {val:6.2%}')【実行結果】
テキスト記載の通り、分散比が1未満の確率は1%未満です。

【分析】~テキストにならって
CMを見ていないグループの方が分散が大きいことから、CM認知がブランド評価の「均一化」(バラツキが小さい方向の均一化)に寄与すると考えられます。

【分析3】11.5.3 もしドコモのCM評価がauと同一だったら?
ブランド評価の高いドコモのCM評価がau並みに高くなったら、ブランド評価にどのように変化するかを推論します。
テキスト128ページの乱数発生を行って、CM評価がドコモのままのドコモのブランド評価、CM評価がauと同等だった場合のドコモのブランド評価の予測分布を推論します。
最初に、乱数生成と表11.6の作成を実行します。
Rスクリプト記載の処理ロジックをお借りしてます。
### ドコモのCM評価・auと同一のCM評価の比較 ※表11.6に相当 1分10秒
## 初期値設定
# 推論データから事後分布サンプリングデータを取り出し
out = idata.posterior
out2 = idata2.posterior
# 各種初期値
sn = 1000 # サンプル作成数
m = 3 # ブランド数
num_iter = 4000 # MCMCサンプリング数 draw × chain
b01_sim = np.hstack([np.ones((sn, 1)), np.zeros((sn, m-1))]) # 切片
# 空の変数の用意
mean_mat = np.empty(shape=(num_iter, 2))
var_mat = np.empty(shape=(num_iter, 2))
es3 = np.empty(shape=num_iter)
no3 = np.empty(shape=num_iter)
pd3 = np.empty(shape=num_iter)
y_ie = []
y_if = []
# 事後分布サンプリングデータ1件毎に繰り返し処理 Rスクリプトに準拠
for i in range(num_iter):
# パラメータを取り出す
p11_i = out2.P.stack(sample=('chain', 'draw')).data[0, 0, i]
p21_i = out2.P.stack(sample=('chain', 'draw')).data[0, 1, i]
mu11_i = out2.mu1.stack(sample=('chain', 'draw')).data[0, 0, i]
mu21_i = out2.mu1.stack(sample=('chain', 'draw')).data[0, 1, i]
m21_i = out2.mu2.stack(sample=('chain', 'draw')).data[0, :, i]
mu22_i = out2.mu1.stack(sample=('chain', 'draw')).data[1, 1, i]
m22_i = np.array(
[(out2.mu2.stack(sample=('chain', 'draw')).data[0, 0, i]),
(out2.mu2.stack(sample=('chain', 'draw')).data[1, 1, i])])
v11_i = out2.sigma1.stack(sample=('chain', 'draw')).data[0, 0, i]
v21_i = out2.sigma1.stack(sample=('chain', 'draw')).data[0, 1, i]
v1_i = out2.covs.stack(sample=('chain', 'draw')).data[0, :, :, i]
# 通常通りのドコモの予測分布
D_i = np.hstack([stats.binom.rvs(n=1, p=p11_i, size=sn).reshape(-1, 1),
stats.binom.rvs(n=1, p=p21_i, size=sn).reshape(-1, 1)])
D_tf = D_i @ (1, 2)
z10_i = np.vstack([
stats.norm.rvs(loc=mu11_i, scale=np.sqrt(v11_i), size=sn), [0]*sn]).T
z01_i = np.vstack([
[0]*sn, stats.norm.rvs(loc=mu21_i, scale=np.sqrt(v21_i), size=sn)]).T
z11_i = ((np.repeat(m21_i, sn).reshape(2, sn) + np.linalg.cholesky(v1_i).T
@ stats.norm.rvs(loc=0, scale=1, size=(2, sn))).T)
DZ_i = (np.where(D_tf==1, 1, 0).reshape(-1, 1) * z10_i
+ np.where(D_tf==2, 1, 0).reshape(-1, 1) * z01_i
+ np.where(D_tf==3, 1, 0).reshape(-1, 1) * z11_i)
mu_i = (np.hstack([b01_sim, D_i, DZ_i])
@ out.beta.stack(sample=('chain', 'draw')).data[:, i])
s2_i = (np.exp(np.hstack([b01_sim, D_i])
@ out.gamma.stack(sample=('chain', 'draw')).data[:, i]))
y1_i = mu_i + np.sqrt(s2_i) * stats.norm.rvs(loc=0, scale=1, size=sn)
mean_y1 = y1_i.mean()
var_y1 = y1_i.var()
mean_mat[i, 0] = mean_y1
var_mat[i, 0] = var_y1
# ドコモのCM評価の平均がauと同じだったらの予測分布
D_i = np.hstack([stats.binom.rvs(n=1, p=p11_i, size=sn).reshape(-1, 1),
stats.binom.rvs(n=1, p=p21_i, size=sn).reshape(-1, 1)])
D_tf = D_i @ (1, 2)
z10_i = np.vstack(
[stats.norm.rvs(loc=mu11_i, scale=np.sqrt(v11_i), size=sn), [0]*sn]).T
z01_i = np.vstack(
[[0]*sn, stats.norm.rvs(loc=mu22_i, scale=np.sqrt(v21_i), size=sn)]).T
z11_i = ((np.repeat(m22_i, sn).reshape(2, sn) + np.linalg.cholesky(v1_i).T
@ stats.norm.rvs(loc=0, scale=1, size=(2, sn))).T)
DZ_i = (np.where(D_tf==1, 1, 0).reshape(-1, 1) * z10_i
+ np.where(D_tf==2, 1, 0).reshape(-1, 1) * z01_i
+ np.where(D_tf==3, 1, 0).reshape(-1, 1) * z11_i)
mu_i = (np.hstack([b01_sim, D_i, DZ_i])
@ out.beta.stack(sample=('chain', 'draw')).data[:, i])
s2_i = (np.exp(np.hstack([b01_sim, D_i])
@ out.gamma.stack(sample=('chain', 'draw')).data[:, i]))
y2_i = mu_i + np.sqrt(s2_i) * stats.norm.rvs(loc=0, scale=1, size=sn)
mean_y2 = y2_i.mean()
var_y2 = y2_i.var()
mean_mat[i, 1] = mean_y2
var_mat[i, 1] = var_y2
# 2つの分散
var_y = np.var(np.hstack([y1_i, y2_i]))
# 予測分布の描画用変数 :テキストと違う方法で保存
y_ie.append(y1_i)
y_if.append(y2_i)
# 効果量
es3[i] = (mean_y2 - mean_y1) / np.sqrt(var_y)
# 非重複度
no3[i] = stats.norm.cdf(x=mean_y2, loc=mean_y1, scale=np.sqrt(var_y))
# 優越率
pd3[i] = np.mean(y1_i < y2_i)
# データフレーム化
stats_df4 = pd.DataFrame({'効果量': [es3.mean(), es3.std()],
'非重複度': [no3.mean(), no3.std()],
'優越率': [pd3.mean(), pd3.std()]},
index=['平均', '標準偏差']).T
display(stats_df4.round(3))【実行結果】
テキストの結果ととほぼ一致しています。

続いて、図11.3の予測分布の描画を行います。
### ドコモのブランド評価y_ieとauと同等の場合のドコモのブランド評価y_ifの描画
# ※図11.3に相当
## データの準備
# y_ie,y_ifを1次元にフラット化
y_ie_flat = np.array(y_ie).flatten()
y_if_flat = np.array(y_if).flatten()
# y_ie,y_ifの中央値の算出
y_ie_med = np.median(y_ie_flat)
y_if_med = np.median(y_if_flat)
# y_ie,y_ifの推論値から描画用に10000個をランダムに取り出し
np.random.seed(1234)
y_ie_plot = np.random.choice(y_ie_flat, 10000, replace=False)
y_if_plot = np.random.choice(y_if_flat, 10000, replace=False)
## 描画
fig, ax = plt.subplots(1, 1)
# y_ieのKDEプロットの描画
kde_plot_ie = sns.kdeplot(y_ie_plot, color='tab:blue',
label='$y_{ie}$ : ドコモのまま', ax=ax)
# y_ifのKDEプロットの描画
kde_plot_if = sns.kdeplot(y_if_plot, color='tomato', ls='--',
label='$y_{if}$ : auと同等', ax=ax)
## 最頻値=MAP推定値の算出と描画
# KDEプロットで描画した線から、x軸,y軸の全値を取得
kde_data_ie = kde_plot_ie.get_lines()[0].get_data()
kde_data_if = kde_plot_if.get_lines()[1].get_data()
# KDEプロットのyの最大値(最頻値)のインデックスを取得
kde_max_idx_ie = kde_data_ie[1].argmax()
kde_max_idx_if = kde_data_if[1].argmax()
# KDEプロットのyの最大値≒MAP推定値の垂直線の描画
ax.vlines(x=kde_data_ie[0][kde_max_idx_ie], ymin=0,
ymax=kde_data_ie[1][kde_max_idx_ie], color='tab:blue')
ax.vlines(x=kde_data_if[0][kde_max_idx_if], ymin=0,
ymax=kde_data_if[1][kde_max_idx_if], color='tomato', ls='--')
## 修飾
ax.set(xlim=[-4, 4], ylim=[0, 0.4], xticks=np.linspace(-4, 5, 10),
yticks=np.linspace(0, 0.4, 5))
ax.grid(lw=0.5)
ax.legend();【実行結果】
赤い点線の「CM評価がauと同等」の方が若干、値が大きい結果になりました。

【分析】~テキストにならって
効果量0.149は偏差値換算で1程度。CM評価をau並みに向上させることでブランド評価は向上するといえるけれども、大きな向上にはなりそうにないです。
テキストは「CM評価によって効果量を0.3上昇させるには、CM評価をau並みにするだけでなく、さらなる改善が必要にあることがわかるだろう」としています。

【分析4】11.5.4 auがドコモのシェアを奪っていったら?
auがドコモの利用シェアを奪った場合、利用者増加によってauのブランド評価がどのように変化するかをシミュレーション的に推論します。
テキスト図11.4を描画して、ドコモ利用率を1%ずつ減少・au利用率を1%ずつ増加させていき、両ブランドの平均の変化と、auがドコモのブランド評価を上回るポイントを探ります。
Rスクリプト記載の事後分布の算出処理ロジックをお借りして、事後分布データを生成します。
### ドコモ・auのブランド評価の平均μ_y^(j)を算出 1分
# Rスクリプトを単純翻訳、目的の変数は mu_sim
# 初期値設定
rng = np.arange(-1, 12) # -1, 0, 1, ・・・, 11%
sn = len(rng) # 13
mu_sim = np.empty((num_iter, sn, 2)) # shape(4000, 13, 2)
b01_sim = np.zeros((sn, m))
b02_sim = np.zeros((sn, m))
b01_sim[:, 0] = np.ones((sn))
b02_sim[:, 1] = np.ones((sn))
# 事後分布サンプリングデータ1個づつ繰り返し処理
for i in range(num_iter):
# ドコモの事後平均
p11_i = out2.P.stack(sample=('chain', 'draw')).data[0, 0, i] - rng/100 # -
p11_i = np.where(p11_i < 0, 0, p11_i)
p11_i = np.where(p11_i > 1, 1, p11_i)
p21_i = out2.P.stack(sample=('chain', 'draw')).data[0, 1, i]
mu11_i = out2.mu1.stack(sample=('chain', 'draw')).data[0, 0, i]
mu21_i = out2.mu1.stack(sample=('chain', 'draw')).data[0, 1, i]
m1_i = out2.mu2.stack(sample=('chain', 'draw')).data[0, :, i]
D_i = np.c_[p11_i, np.repeat(p21_i, len(rng))]
DZ1_i = (D_i[:, 0] * (1 - D_i[:, 1]) * mu11_i
+ D_i[:, 0] * D_i[:, 1] * m1_i[0])
DZ2_i = ((1 - D_i[:, 0]) * D_i[:, 1] * mu21_i
+ D_i[:, 0] * D_i[:, 1] * m1_i[1])
mu_i = (np.c_[b01_sim, D_i, DZ1_i, DZ2_i]
@out.beta.stack(sample=('chain', 'draw')).data[:, i])
mu_sim[i, :, 0] = mu_i
# auの事後平均
p12_i = out2.P.stack(sample=('chain', 'draw')).data[1, 0, i] + rng/100 # +
p12_i = np.where(p12_i < 0, 0, p12_i)
p12_i = np.where(p12_i > 1, 1, p12_i)
p22_i = out2.P.stack(sample=('chain', 'draw')).data[1, 1, i]
mu12_i = out2.mu1.stack(sample=('chain', 'draw')).data[1, 0, i]
mu22_i = out2.mu1.stack(sample=('chain', 'draw')).data[1, 1, i]
m2_i = out2.mu2.stack(sample=('chain', 'draw')).data[1, :, i]
D_i = np.c_[p12_i, np.repeat(p22_i, len(rng))]
DZ1_i = (D_i[:, 0] * (1 - D_i[:, 1]) * mu12_i
+ D_i[:, 0] * D_i[:, 1] * m2_i[0])
DZ2_i = ((1 - D_i[:, 0]) * D_i[:, 1] * mu22_i
+ D_i[:, 0] * D_i[:, 1] * m2_i[1])
mu_i = (np.c_[b02_sim, D_i, DZ1_i, DZ2_i]
@out.beta.stack(sample=('chain', 'draw')).data[:, i])
mu_sim[i, :, 1] = mu_i
## まとめ
# ドコモ
mu_d = np.c_[mu_sim[:, 1:-1, 0].mean(axis=0),
mu_sim[:, 1:-1, 0].std(axis=0),
np.quantile(mu_sim[:, 1:-1, 0], q=0.025, axis=0),
np.quantile(mu_sim[:, 1:-1, 0], q=0.975, axis=0),
]
mu_d_df = pd.DataFrame(mu_d, columns=['EAP', 'post.sd', '2.5%CI', '97.5%CI'],
index=[f'-{i}%' for i in range(len(mu_d))]).round(3)
# au
mu_a = np.c_[mu_sim[:, 1:-1, 1].mean(axis=0),
mu_sim[:, 1:-1, 1].std(axis=0),
np.quantile(mu_sim[:, 1:-1, 1], q=0.025, axis=0),
np.quantile(mu_sim[:, 1:-1, 1], q=0.975, axis=0)]
mu_a_df = pd.DataFrame(mu_a, columns=['EAP', 'post.sd', '2.5%CI', '97.5%CI'],
index=[f'+{i}%' for i in range(len(mu_d))]).round(3)
【実行結果】なし
算出した事後分布の要約統計量を表示します。
### 要約統計量の表示
print('【ドコモ:利用率を-1%づつ変化させた場合のドコモのブランド評価】')
display(mu_d_df)
print('【au:利用率を+1%づつ変化させた場合のauのブランド評価】')
display(mu_a_df)【実行結果】
おおまかな数値を掴めたのではないでしょうか。

事後分布データ mu_sim に基づいて、テキスト図11.4を描画します。
### auがドコモのシェアを奪った場合の両社のブランド評価の描画 ※図11.4に相当
# 初期値設定:x軸目盛ラベル
x = range(0, 11)
# 描画領域の指定
fig, ax = plt.subplots(1, 3, figsize=(12, 4))
### ドコモの利用率の描画
## プロット用データの算出:事後平均・95%CI・50%CI
means_d = mu_sim[:, 1:-1, 0].mean(axis=0)
ci95_d = np.quantile(mu_sim[:, 1:-1, 0], q=[0.025, 0.975], axis=0)
ci50_d = np.quantile(mu_sim[:, 1:-1, 0], q=[0.25, 0.75], axis=0)
## 描画
# 事後平均の折れ線グラフの描画
ax[0].plot(x, means_d, color='tab:blue', ls='--')
# 95%CI区間の描画
ax[0].fill_between(x, ci95_d[0], ci95_d[1], color='tab:blue', alpha=0.1)
# 50%CI区間の描画
ax[0].fill_between(x, ci50_d[0], ci50_d[1], color='tab:blue', alpha=0.3)
# 修飾
ax[0].set(xticks=x, xticklabels=[f'-{i}' for i in range(len(means_d))],
xlabel='ドコモの利用率($p_1^{(1)}$)の変化分(%)',
ylabel='ドコモのブランド評価平均 $\\mu_y^{(1)}$')
ax[0].grid(lw=0.3)
### auの利用率の描画
## プロット用データの算出:事後平均・95%CI・50%CI
means_a = mu_sim[:, 1:-1, 1].mean(axis=0)
ci95_a = np.quantile(mu_sim[:, 1:-1, 1], q=[0.025, 0.975], axis=0)
ci50_a = np.quantile(mu_sim[:, 1:-1, 1], q=[0.25, 0.75], axis=0)
## 描画
# 事後平均の折れ線グラフの描画
ax[1].plot(x, means_a, color='tomato', ls='--')
# 95%CI区間の描画
ax[1].fill_between(x, ci95_a[0], ci95_a[1], color='tomato', alpha=0.1)
# 50%CI区間の描画
ax[1].fill_between(x, ci50_a[0], ci50_a[1], color='tomato', alpha=0.3)
# 修飾
ax[1].set(xticks=x, xticklabels=[f'+{i}' for i in range(len(means_a))],
xlabel='auの利用率($p_1^{(2)}$)の変化分(%)',
ylabel='auのブランド評価平均 $\\mu_y^{(2)}$')
ax[1].grid(lw=0.3)
### auのブランド評価平均がドコモを上回る確率の描画
# 上回る確率の算出
a_over_prob = (mu_sim[:, 1:-1, 0] < mu_sim[:, 1:-1, 1]).mean(axis=0)
# 上回る確率の描画
ax[2].plot(x, a_over_prob)
# y=0.5の赤点線の描画
ax[2].axhline(0.5, color='tab:red', ls='--')
# 修飾
ax[2].set(xticks=x, xticklabels=[f'±{i}' for i in range(len(means_a))],
xlabel='ドコモ利用率(-), au利用率(+)の変化分(%)',
ylim=(0.0, 1.0), yticks=np.arange(0, 1.1, 0.1),
ylabel='auのブランド評価がドコモを上回る確率')
ax[2].grid(lw=0.3)
plt.tight_layout()
plt.show()【実行結果】
ドコモ利用率 5~6%減、au利用率 5~6%増あたりで、auのブランド評価がドコモを上回る確率が50%になりました。

以上で第11章は終了です。

おわりに
事後分布・予測分布とシミュレーション
この章の分析ロジックは凄いです!
凄すぎて後半の2つは理解が追いつきませんでした(汗)
Rスクリプトの動きを解析してPythonコードに翻訳することで精一杯。
同類のロジックを自分で作り出すことは現段階では諦めています。
でもでもMCMCサンプリングデータを使って、さらに予測分布のサンプリングを行って、「もしも~だったら」の確率(点推定では無く)をシミュレーションできるベイズモデリング・ベイズプログラミングのパワーをヒシヒシと感じました。
ますます魅力(魔力?)に取り憑かれた次第です。
おわり

シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
