
第18章「本当に麻雀が強いのは誰か?」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング」の第18章「本当に麻雀が強いのは誰か?」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
この章では、4人の麻雀ポイントデータを用いて、ベイズモデリングで「誰が強いのか」を推論します。
とてもシンプルな構造で実力差を推論できるパワフルなモデルです。
さあ一緒に、PyMCのベイズモデリングのロンへ出かけましょう!

テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 杣取恵太 先生
モデル難易度: ★・・・・ (やさしい)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★★★& GoooD! \\
結果再現度 & ★★★★★& 最高✨ \\
楽しさ & ★★★★★& 楽しい! \\
\end{array}
$$

評価ポイント
一発で収束できて、しかもテキストとほぼ同じ結果になりました。
リーチ一発ツモドラドラです!
工夫・喜び・反省
尤度にディリクレ分布を使うこと、ほんの数行のモデル、データ前処理時や事後分布サンプルデータ活用時の工夫、などなど、さまざまな知見をいただくことができました。
モデルの概要
テキストの調査・実験の概要
■ 分析対象データ
同一メンバー4名・22日間・合計143半荘の麻雀ポイントデータです。
麻雀がほんとうに好きなんですね!
■ ソフトマックス関数とディリクレ分布
麻雀のポイント合計は常に一定(ゼロ)である特徴を捉えて、次のようにモデリングします。
半荘ポイントデータにソフトマックス関数を適用して、半荘ごとの総和が1になるように前処理する
前処理後のポイントデータはディリクレ分布に従うと仮定する
※ディリクレ分布は「合計が1になる確率のベクトル」を生成する分布
ソフトマックス関数はニューラルネットワークの活性化関数に用いられるアレです。
テキストの数式をお借りして、半荘ポイントを変換するソフトマックス関数の数式を掲載します。
$$
point_{it} = \cfrac{\exp(\alpha_{it})}{\sum^4_i \exp(\alpha_{it})} \\
\\
(i=1, \cdots, 4,\ t=1, \cdots, 143)
$$
ソフトマックス関数適用後の半荘ポイント$${point_{it}}$$は、次の要領で計算されます。
プレイヤー$${i}$$の半荘$${t}$$における変換前ポイント$${\alpha_{it}}$$を指数変換($${\exp}$$)します。
指数変換した4人分の変換前ポイントの総和で割って求めます。
1つの要素を要素全体の合計で割るので、合計が1になるのです。
半荘$${t=1}$$の変換後半荘ポイント$${point_{i1}}$$を例にすると、プレイヤー4人全員分を合計すると1になります。
($${point_{11} + point_{21} + point_{31} + point_{41}=1}$$)
モデリングの全体像を図示します。

テキストのモデリング
■目的変数と関心のあるパラメータ
目的変数は、ソフトマックス関数で前処理した後の麻雀ポイント$${point}$$です。
関心のあるパラメータはずばり雀力$${janryoku}$$です。
このモデルで雀力は「麻雀ポイントからのみ推測する能力」として捉えられています。
■ モデル数式
超シンプルです!
添字$${t}$$は$${t}$$回目の半荘、$${point}$$横の数字はプレイヤーIDを示します。
$$
\begin{align*}
\overrightarrow{point_{t}} &\sim \text{Dirichlet}\ (\overrightarrow{janryoku}) \\
\overrightarrow{point_{t}} &= (point1_t, point2_t, point3_t, point4_t)
\end{align*}
$$
パラメータ$${janryoku}$$の事前分布はテキストに記載はありませんでした。
なお、Stanの変数定義では、$${janryoku}$$は0以上とされています。

■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルの推論値を利用した分析は「PyMC実装」章をご覧ください。
PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
import scipy.stats as stats
# PyMC
import pymc as pm
import arviz as az
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込み
csvファイルをpandasのデータフレームに読み込みます。
### データの読み込み
# データの読み込み
data_orgn = pd.read_csv('pointData.csv')
# データの表示
display(data_orgn)【実行結果】
全143行(半荘)です。
4つの列に4人のプレイヤーの麻雀ポイントが記録されています。

3.データの外観の確認
要約統計量を表示します。
### 要約統計量の表示
display(data_orgn.describe().round(2))【実行結果】
平均得点(mean)ではプレイヤーBが強く、プレイヤーCが弱い感じがします。

麻雀ポイントを可視化しましょう。
テキストの図18.1のグラフを描画します。
seaborn の stripplot を利用します。
### 各プレイヤーのポイントの描画 ※図18.1に相当
# 各プレイヤーの散布図(stripplot)の描画
sns.stripplot(data=data_orgn, color='tab:blue', alpha=0.5)
# 各プレイヤーの平均ポイントを折れ線グラフで描画
plt.plot(data_orgn.mean(axis=0), 'o-', color='red')
# 修飾
plt.grid(lw=0.5)
plt.xlabel('プレイヤー')
plt.ylabel('ポイント')
plt.show()【実行結果】
ポイントのバラツキが大きいです!
バラツキと比べると各プレイヤーの平均ポイントは、どんぐりの背比べ、かもですね!

4.データの前処理
ソフトマックス関数を使って各行の合計が1になるようにデータの前処理を行います。
### データの前処理:ソフトマックス関数で変換
# softmax関数の定義
def softmax(row):
return [np.exp(row[i]) / sum(np.exp(row)) for i in range(len(row))]
# 300で割る(Rコードどおり)
data = data_orgn.copy()
data = data / 300
# ソフトマックス関数を適用して行単位の総和が1になるようにする
data = data.apply(softmax, axis=1, result_type='expand')
data.columns = data_orgn.columns
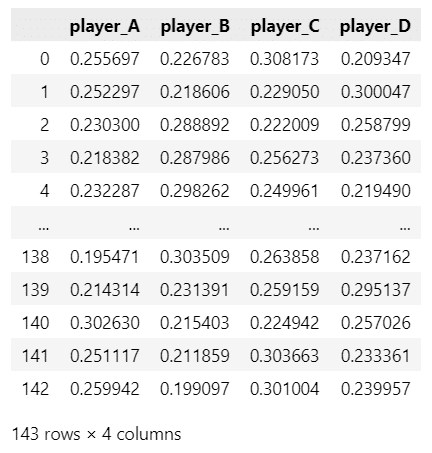
display(data)【実行結果】
前処理後の値をざっと眺めますと、どのプレイヤーも「0.2~0.3」あたりの値になっています。
モデル構築の前に、ぜひディリクレ分布をチェックしましょう!
scipy.stats の dirichlet を利用します。
パラメータが1つ、2つ、3つのケースでディリクレ分布の乱数を作成して、合計が1になることを確認します。
### ディリクレ分布の例
np.random.seed(2)
alphas = [[1], [1, 1], [1, 1, 1]]
for alpha in alphas:
stat = stats.dirichlet.rvs(alpha=alpha)
print(f'パラメータ {alpha}⇒ ディリクレ分布の乱数: {stat} 合計={stat.sum()}')【実行結果】
ディリクレ分布の乱数(確率)の合計は1になりました!


モデル構築
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$$
\begin{align*}
janryoku &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100,\ \text{dims}=player)\\
likelihood &\sim \text{Dirichlet}\ (\text{a}=janryoku,\ \text{dims}=(data,\ player)) \\
\end{align*}
$$
1.モデルの定義
数式表現を実直にモデル記述します。
### モデルの定義
# カテゴリ変数の要素とインデックスの取得
player_cat = pd.Categorical(data.columns).categories
player_idx = pd.Categorical(data.columns).codes
# モデルの定義
with pm.Model() as model:
### データ関連定義
# coordの定義
model.add_coord('data', values=data.index, mutable=True)
model.add_coord('player', values=player_cat, mutable=True)
# dataの定義
point = pm.ConstantData('point', value=data, dims=('data', 'player'))
### 事前分布
janryoku = pm.Uniform('janryoku', lower=0, upper=100, dims='player')
### 尤度
likelihood = pm.Dirichlet('likelihood', a=janryoku, observed=point,
dims=('data', 'player'))【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の2つを設定しました。
・データの座標:名前「data」、値「dataのindex」
・プレイヤーの座標:名前「player」、値「dataのcolumns」dataの定義
目的変数である麻雀ポイント$${point}$$です。
形状は shape=( 143, 4 ) です。パラメータの事前分布
パラメータ$${janryoku}$$は範囲が$${[0, 100]}$$の一様分布にしました。
形状は shape=4 です。尤度
ディリクレ分布です。形状は shape=( 143, 4 ) です。
2.モデルの外観の確認
# モデルの表示
model【実行結果】
シンプル・イズ・ベスト!

# モデルの可視化
pm.model_to_graphviz(model)【実行結果】
シンプル・イズ・ベスト,2!

3.事後分布からのサンプリング
乱数生成数はテキストよりも多めにしています。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ10秒でした。爆速!
### 事後分布からのサンプリング 10秒
# テキストはdraws=500, tune=500, chains=4
with model:
idata = pm.sample(draws=5000, tune=1000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=123)【実行結果】(一部)

4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
rhat_idata = az.rhat(idata)
(rhat_idata > 1.1).sum()【実行結果】
$${\hat{R} > 1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。
ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata, hdi_prob=0.95).round(3)【実行結果】
平均値が 43~46 付近で拮抗している感じがします。

トレースプロットで事後分布サンプリングデータの様子を確認します。
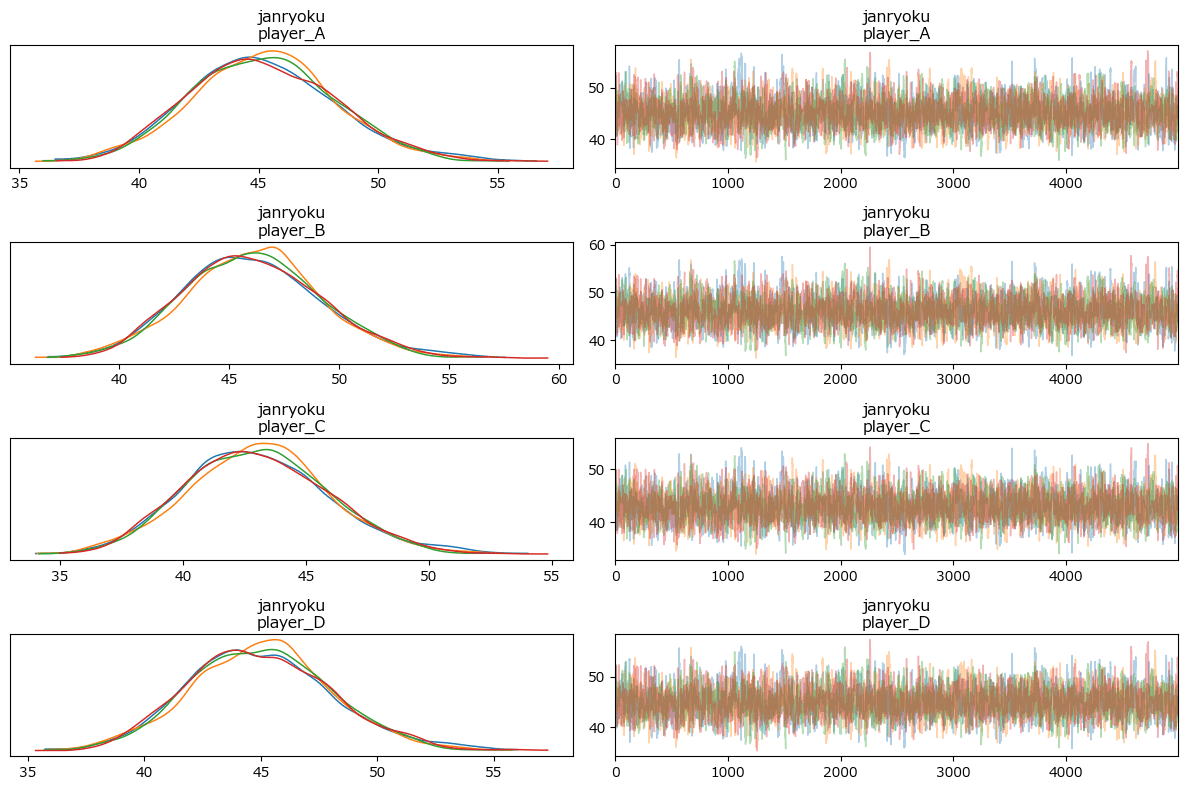
### トレースプロットの表示
pm.plot_trace(idata, compact=False)
plt.tight_layout();【実行結果】
収束している感じがします。

5.分析
パラメータの事後分布プロットを描画しましょう。
テキストの図18.2に相当します。
plot_posterior() で簡単に描画!
### 事後分布プロット ※図18.2に対応
pm.plot_posterior(idata, hdi_prob=0.95, figsize=(10, 3))
plt.tight_layout();【実行結果】
平均値meanと95%HDIに注目します。
テキストの解説のとおり、プレイヤーA、B、Dの雀力は拮抗している感じです。

続いて、テキストの表18.2に相当する「プレイヤー間の雀力に差がある確率」の表を作成します。
### 雀力の差の確率の算出 ※表18.2に対応
# 初期値設定
janryoku_mtx = np.zeros((4,4))
# 雀力の事後分布サンプリングデータの格納
janryoku_post = idata.posterior.janryoku.data.reshape(20000, 4).T
# プレイヤー間の雀力に差がある確率の算出
for i in range(4):
for j in range(4):
janryoku_mtx[i, j] = (janryoku_post[i] > janryoku_post[j]).mean()
# データフレーム化
col_names = ['A氏', 'B氏', 'C氏', 'D氏']
janryoku_df = pd.DataFrame(janryoku_mtx, index=col_names, columns=col_names)
# データフレームの表示
print('【プレイヤー間の雀力に差がある確率】')
display(janryoku_df.round(2))【実行結果】
行が主語、列が対戦相手です。
確率値はほぼテキストと同じです。
プレイヤーBが圧倒的に勝ちやすい、プレイヤーCが圧倒的に負けやすい、こんな感じでしょうか。
プレイヤーAとDは若干Aのほうが勝ちやすい(60%)ようです。

最後にプレイヤー間の散布図で相関を確認します。
テキストによると「プレイヤーごとの$${janryoku}$$パラメータの相関が非常に高い」とのこと。
相関係数の算出には NumPy の corrcoef 関数を利用しました。
また、散布図行列の描画には seaborn の ペアプロットを利用しました。
「# 散布図に45度線の描画, 相関係数の表示」の箇所では、力技でグラフ上に45度線と相関係数の値を重ねています。for 文でグラフオブジェクト? g の axes を取り出して線とテキストを上書き処理するイメージです。
### 散布図行列 ★図18.3の対応
# 相関係数の算出
jan_corr = np.corrcoef(janryoku_post).ravel()
# 散布図行列の描画
g = sns.pairplot(pd.DataFrame(janryoku_post.T, columns=col_names),
kind='scatter', diag_kind='hist',
plot_kws={'marker': 'o', 'alpha': 0.2, 'ec': 'white'},
diag_kws={'bins': 30, 'edgecolor': 'white'}
);
# 散布図に45度線の描画, 相関係数の表示
for i, (ax, cor) in enumerate(zip(g.axes.ravel(), jan_corr)):
if i % 5 != 0:
ax.plot([30.1, 64.9], [30.1, 64.9], color='red', ls='--')
ax.text(50, 32, f'Corr: {cor:.3f}', fontsize=12)
# 修飾
g.fig.suptitle('各プレイヤーの雀力に関する散布図行列')
g.set(xlim=(30, 65), ylim=(30, 65))
plt.tight_layout();【実行結果】
めっちゃ相関してます!
赤い点線よりも上(左)に点が多いプレイヤーの方が強い、こんな見方をします。

やはりプレイヤーBが強そうですね。
テキスト197ページの結論の根拠になっている「プレイヤーBが他のプレイヤーよりも雀力が高い確率」を計算しましょう。
式は長いですが、2プレイヤー間でBのポイントが上回る回数をそれぞれ計算して、全回数で割って平均を算出しています。
### プレイヤーBが他のプレイヤーよりも強い確率の計算 ※テキスト197ページ
print('プレイヤーBが他のプレイヤーよりも強い確率: ',
round((
sum(janryoku_post[1] - janryoku_post[0] > 0)
+ sum(janryoku_post[1] - janryoku_post[2] > 0)
+ sum(janryoku_post[1] - janryoku_post[3] > 0))
/ (20000*3), 3)
)【実行結果】
テキストどおり、確率は$${0.928 \fallingdotseq 0.93}$$です。

【総合判定】
プレイヤーBが一番強い、と言えそうです。
テキストもB氏が最も雀力が高いとしています。

6.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idataをpickleで保存します。
### idataの保存 pickle
file = r'idata_ch18.pkl'
with open(file, 'wb') as f:
pickle.dump(idata, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_ch18.pkl'
with open(file, 'rb') as f:
idata_load = pickle.load(f)以上で第18章は終了です。
おわりに
ゼロサムゲーム
ゲーム参加者の得点と失点の「合計がゼロ」になるゲームをゼロサムゲームと呼ぶそうです。
麻雀もゼロサムゲーム。
そういえば、ソフトマックス関数を適用して「合計が1」になるようにデータの前処理を行いました。

ところで、RとStanで書かれたベイズモデリングをPythonとPyMCに書き換えて動かす作業はゼロサムでしょうか?
分布が収束してテキストの結果に近づけたときは+++、$${\hat{R}}$$が激しい値となり愕然とするときは---、みたいなPyMC化のプロセスで沸き立つ感情=効用には、プラスのときもマイナスのときもあります。
ちなみに、原稿を作成する作業においては、時間をコストと思っていないので、プラスに向くかマイナスに陥るかは。自己評価次第(気分次第!?)かもです。
次回の第19章は最終章です。
トータル得点は如何に・・・。

シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ(お題)を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます!
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。
最後までお読みいただきまして、ありがとうございました。
