Generalization of Euler's Formula with Variable Unit Scales and a Proposal for a New Natural Number System

Abstract

This paper proposes a generalization of Euler's formula using a variable common difference $${ k }$$ from arithmetic sequences. By considering ``worlds'' with different unit scales, we redefine the system of natural numbers and the base of the Napier constant in each world. This approach reveals a new mathematical structure encompassing the complex number domain. The research represents a collaboration between human creativity and AI analytical capabilities, marking the dawn of a new era.

Introduction

Euler's formula

$$
e^{i\theta} = \cos\theta + i\sin\theta
$$

is a fundamental equation in complex analysis, linking exponential and trigonometric functions. This study extends the formula and introduces a novel perspective by using the common difference $${ k }$$ from arithmetic sequences as a key to bridging different mathematical ``worlds.''

Paper

67390c2a-D-Generalization of Euler's Formula with Variable Unit Scales and a Proposal for a New Natural Number System.pdf

160 KB

ファイルダウンロードについて

ダウンロード

Graph

View from directly below or directly above (shifted for visualization purposes)

3D display, plotting with gradually decreasing resolution of complex plane rotation

3D front view, plot with gradually decreasing resolution of complex plane rotation

The growth index e^iθ of the complex world is displayed in 3D.
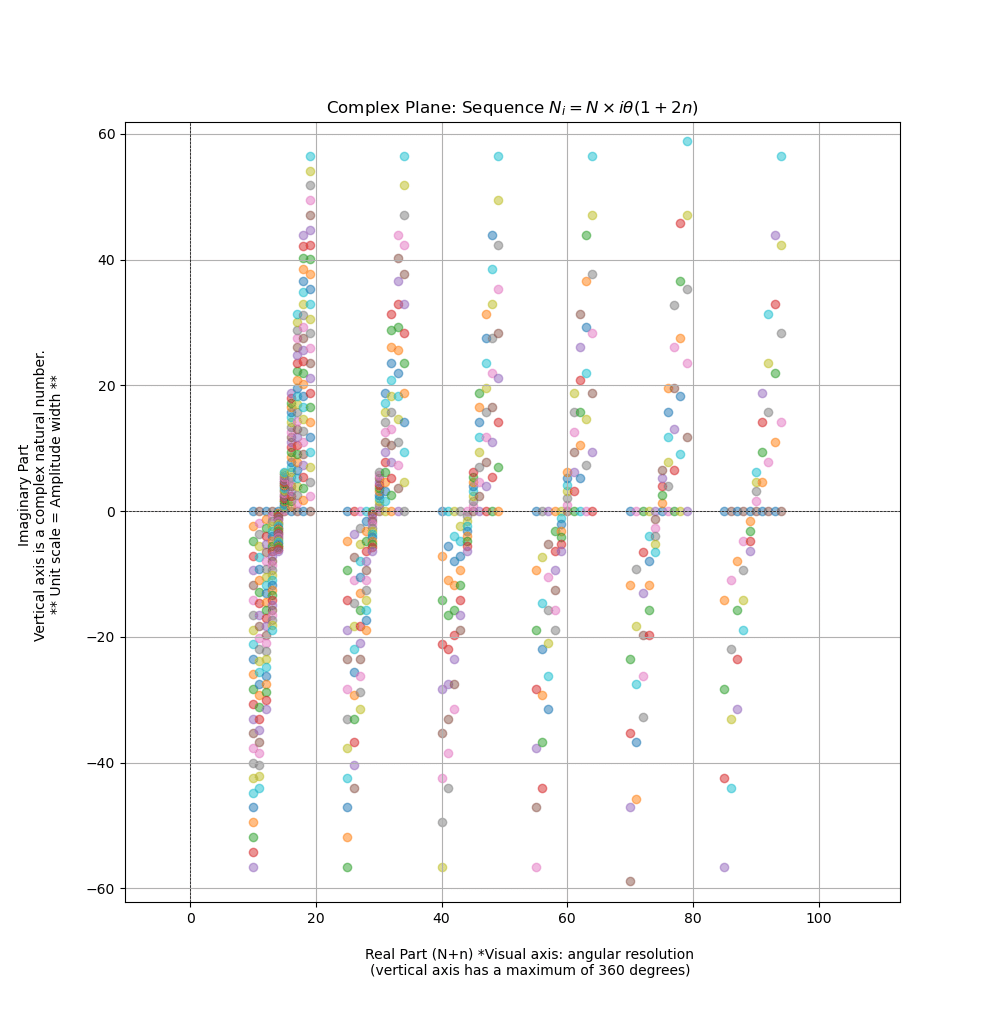
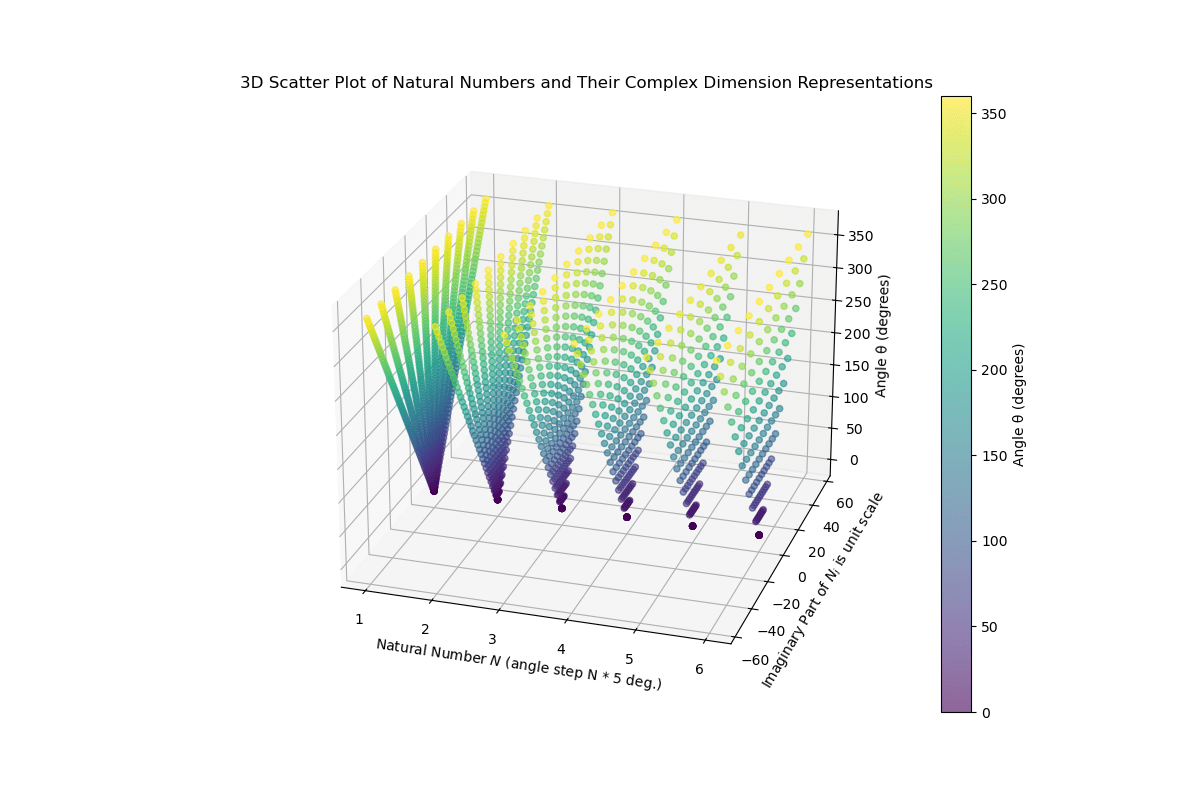
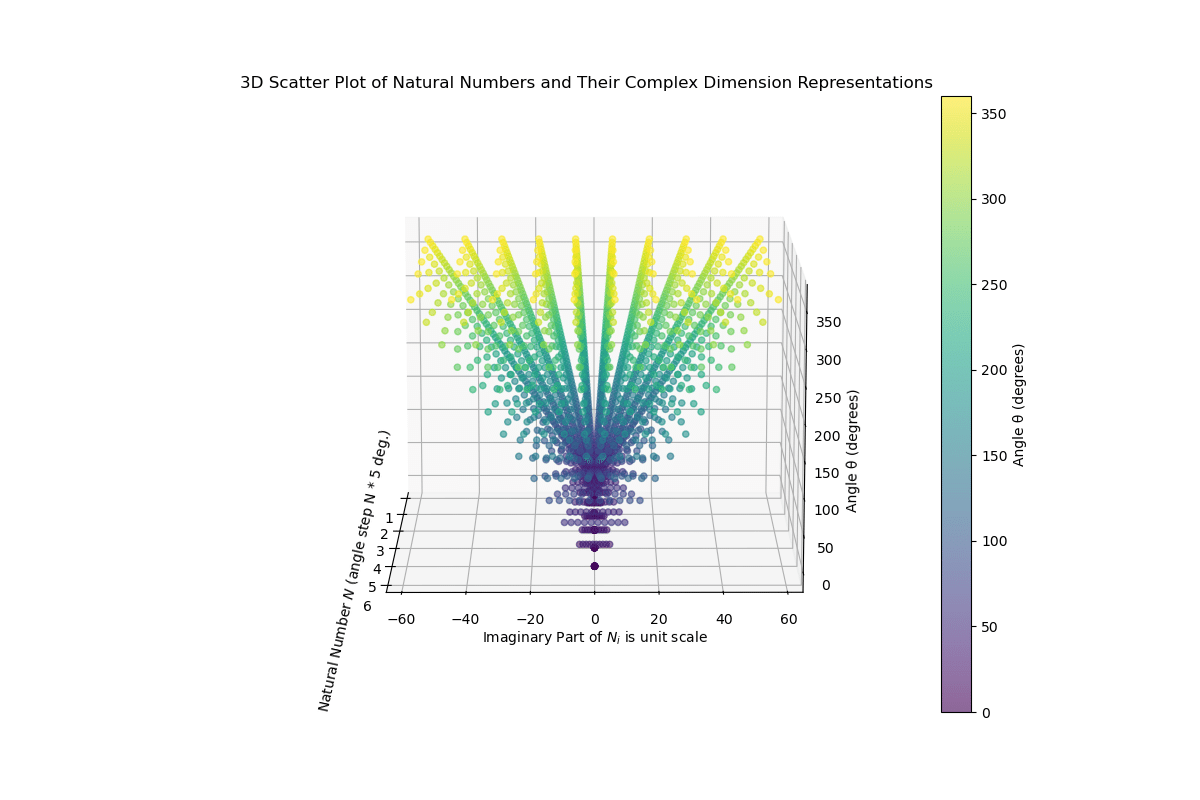
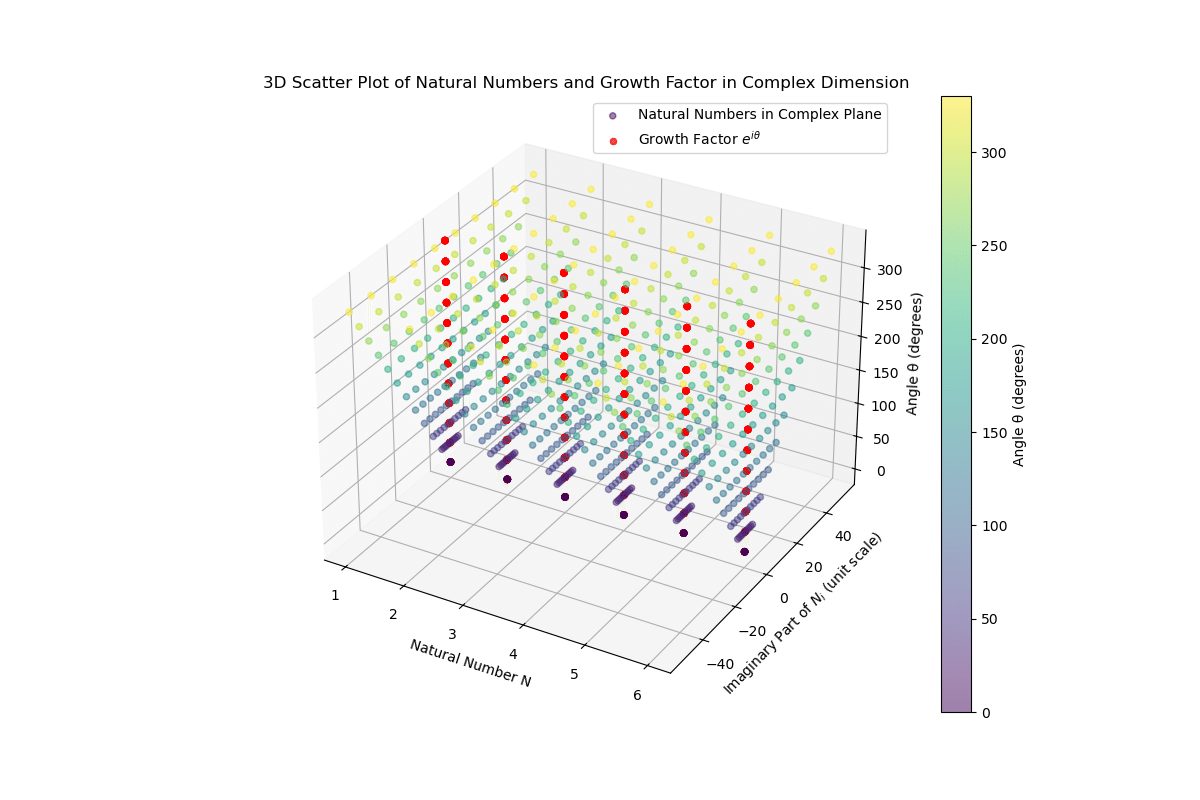
The resolution of the complex plane rotation is constant.

Python plot calculation part

def generate_complex_sequence(
    real_values, imaginary_values, th_start=0, th_end=360, th_step=30
):
    """Generate a sequence of complex numbers and associated angles."""
    complex_numbers = []
    growth_factors = []  # List to store growth index
    for r in real_values:
        for n in imaginary_values:
            for theta_deg in range(th_start, th_end, th_step):
                theta = np.deg2rad(theta_deg)
                k = 1j * theta * (1 + 2 * n)
                ni = (r + n) + k
                complex_numbers.append((r, ni, theta_deg))

                # Calculation of the growth exponent e^{iθ}
                e_k = np.exp(1j * theta)
                growth_factors.append(
                    (r, e_k.imag, theta_deg)
                )  # Preserves real and imaginary parts and angles

    return complex_numbers, growth_factors

---