電気回路（交流）の理論計算について

以前に「ネイピア数」について記事にした際に、応用例として電気回路の話をしたのだが、必要なことを省いて書いてしまったと反省していた。

高専の時に学習した内容だが、その時の記憶をそのまま書いていたため、専門的な用語ばかりで理解しにくい内容になってしまったのだ。この手のことをうまく伝えらえる人は本当にすごいと思う。

今回は電気回路の計算に関する入門編と位置付けて、これから知識として必要な人に向けて書くことにする。

今回の記事は「ネイピア数の使い道」で書いたことを、詳細化したものである。少なくとも前回の時より分かりやすくなっている（筈である）。

前提知識（登場する素子について）

電気回路の授業は基本的に大学（高専）で学習する内容である。この記事を読む対象（ターゲット）は、以下のような人たちを想定している。

・大学で電気回路について学習する予定の人
・電験（電気主任技術者試験）を受ける予定の人
・電気回路について個人的に興味がある人

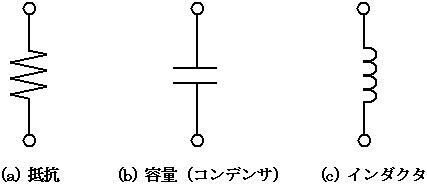
ネイピア数の話の時にも書いたことだが、電気回路で扱う素子は主に３種類である。これらをまとめて「受動素子」と呼ぶこともある。

ひとつは抵抗であり、既に中学の直流回路の計算で登場している。ここにコイル（インダクタ）とコンデンサの２種類が加わる。この２種類の素子が曲者で、交流回路の計算において、計算を複雑化させる。それぞれの素子の計算上の扱いは後にノートで展開する。

ちなみに、受動素子は入力された電気を消費したり、蓄電・放出したり、エネルギー変換したりする。

一方で、入力に対して出力を増大させるような機能をもつ素子もあり、それらは「能動素子」と呼ばれる。トランジスタやダイオードが主に該当する。

前提知識（複素平面）

複素平面の話も前回の時に書いているが、知識としては高校で学習した範囲で十分である。上の絵にある通りである。

なぜ複素平面の考え方が必要かと言うと、直流分（抵抗で消費される電気）と交流分（コイル・コンデンサで消費される電気）を分けて考えるためである。後にそれらを合成することにより、従来（直流回路）の計算方法に載せるのである。

複素平面は計算上のツールに過ぎないが、この計算方法を編み出した人は、本当にすごいと思う。

直流分は実軸（Re）、交流分は虚軸（Im）でプロットされる。直流回路の計算は直流分（実軸）だけ考えれば良いが、交流回路の計算は直流分と交流分の両方の影響を受ける。この辺のやり方も後にノートで展開する。

ノートにまとめてみる

実際に前提条件となる各素子の特徴、複素数表示に置き換えた場合の結果を整理してみた。

ここで、インピーダンスは交流回路における抵抗値の別称である。コイルやコンデンサは入力（正弦関数）から出力（余弦関数）に変換されるように、大きさだけでなく位相も９０度ずれる特性をもつ。

応用例として「共振回路」について書いた。コイルとコンデンサの物性値次第で虚数部が消去されて、極値を迎えるという特徴がある。詳しくは大学以降なり参考書なりで学習することになるだろう。

おわりに

電気回路に関する基礎的な話題について、前回の反省も踏まえて改良してみた。ここでも微分積分が登場するので、毛嫌いしてしまう人もいるかもしれない。

内容を暗記するよりも、意味（本質）を知ることの方が重要だ。これから学習する人には、ぜひチャレンジしてほしいと思いながら書いた。

引き続き、理系的なことを書き続けようと思うので、今後ともよろしくお願いします。