
消費者理論(3):無差別曲線
前回定義した効用関数を用いて、消費者へ同じ効用をもたらす消費の集合を表した無差別曲線を導入し、消費者の好みに関する様々な性質が、無差別曲線の形状にどのような特徴をもたらすかを議論する。連載はこちら。
無差別集合と無差別曲線
ある消費ベクトル$${x}$$に対し、それと同等かより好ましい消費ベクトルの集合である上方位集合$${\{y \in X | y≿x\}}$$、$${x}$$と同等かより好ましくない消費ベクトルの集合である下方位集合$${\{y \in X | x≿y\}}$$を定義した。以下では、$${x}$$と無差別な消費ベクトルの集合である無差別集合を定義する。
無差別集合
消費集合$${X\subset \mathbb{R}^N}$$上の選好関係$${≿}$$が与えられたとき、消費ベクトル$${x\in X}$$と無差別な消費ベクトルからなる集合
$${I(x) = \{y\in X | y∼x\}}$$
を、$${x}$$の無差別集合という。
無差別集合を幾何学的に図示したものが無差別曲線であり、消費者行動の分析に非常に有用な概念である。無差別曲線は選好関係$${≿}$$が連続であれば無数に存在する。
消費者を特徴づける選好関係の仮定
前回までに選好関係$${≿}$$に付与した仮定(合理性と連続性)は、連続な効用関数を定義するのに不可欠な条件であった。ここでは更に、消費者が抱く好みの性質として通常妥当と考えられる仮定を導入し、効用関数に付与することを考える。これらの仮定は前回の合理性、連続性と併せて選好関係$${≿}$$の標準的な公理とも呼ばれるが、分析対象の性質に照らし、仮定の採用は慎重に検討する必要がある。これは数学的な制約ではなく消費者の好みに対する仮定の妥当性という経済学的視点での判断であり、経済学の理論として特徴づけられる議論の一例である。以下では3種類の仮定について言及する。
単調性と強単調性:より多くの消費を好む
選好関係$${≿}$$の単調性または強単調性は、直観的にはどちらも「消費者はより多くの消費を好む」ことを表現している。単調性は、一方の消費ベクトルについて、いくつかの財の消費量が他方の消費ベクトルよりも大きくても、1つでも同じ消費量の財がある場合は両者は弱い選好でしか比較できず、全ての財の消費量が他方の消費ベクトルよりも大きい場合に限り、その消費ベクトルが厳密に選好されることを表す。強単調性は単調性よりも強い仮定であり、ある消費ベクトルの一財でも消費量が他方の消費ベクトルより大きい場合、その消費ベクトルが厳密に選好されることを表す。
消費者を特徴づける選好関係の仮定(1)
任意の消費ベクトル$${x=(x_1, \cdots, x_N)\in X, y=(y_1, \cdots, y_N)\in X}$$の各成分$${i=1, \cdots, N}$$に対して、
単調性:$${x_i≥y_i⇒x≿y}$$および$${x_i>y_i⇒x≻y}$$が成立する。
強単調性:$${x≠y}$$かつ$${x_i≥y_i⇒x≻y}$$が成立する。
一般に、強単調$${⇒}$$単調は成り立つが、その逆は必ずしも成り立つとは言えない(ある財の消費量が増加しても、満足度に影響を与えないケース)。以下で具体例を交えて議論する。
単調だが強単調ではない例:完全補完財
完全補完財とは常に一定割合で消費される2財で、その比率に対する余剰分が一切効用を高めないもの。$${x:y=1:a}$$で消費する場合、$${y=ax}$$の各点を通り、$${x}$$軸、$${y}$$軸に平行なL字型の無差別曲線となる(以下の左図)。例えば、左右セットで使用する靴やコンタクトレンズはいずれも$${1:1}$$の使用を前提としており、右目用のコンタクトの量を一定に保ったまま、左目用のコンタクトだけを大量に購入しても嬉しくも悲しくもない、という状況に該当する。以下の左図の$${u=10}$$の無差別曲線に着目すると、$${x_1}$$(右目用コンタクト)か$${x_2}$$(左目用コンタクト)のいずれかのみを購入した場合に効用は変化せず(例えば$${(x_1, x_2)}$$について$${(3,2)∼(2,2), (5,4)≻(3,3)}$$など)、強単調性は満たさないが単調性は満たす。完全補完財を表すような効用関数の典型例として、以下のようなLeontief型効用関数がある。
Leontief型効用関数
$${u(x_1, x_2)=\min\{ax_1, bx_2\} a>0, b>0}$$
単調かつ強単調の例:完全代替財
完全代替財とは消費者にとって完全に同じ財と見なされる2財で、完全補完財が互いに完全に異なる2財を表しているという意味で、両者は対極的な概念と言える(右目用コンタクトは絶対に左目用コンタクトとして代替的に使用できない)。一般には、無差別曲線は両者の中間に位置する。ある財$${x_1}$$と$${x_2}$$が完全に同じ財(完全代替財)と見なされる時、消費者の効用は両財の消費量の合計のみに依存するため、$${ax_1+bx_2=k a>0, b>0, k=const.}$$が無差別曲線となる。例えば、ビールなら何でも良い消費者に対するアサヒとキリンはこのケースに該当し、アサヒがなければキリンを飲めば同じように満足するため、以下の右図のように無差別曲線は$${x_1+x_2=k k=const.}$$となる。この場合、キリンかアサヒのどちらか一方でも飲む量が増えれば満足度は増し、かつ両方とも飲む量が増えればもちろん満足度は増すため、強単調性と単調性のどちらも満たす。

灰色の領域は、それに接する無差別曲線に対する上方位集合
選好関係$${≿}$$の(強)単調性と効用関数、無差別曲線の形状
効用関数が定義できる前提のもとで、選好関係$${≿}$$が(強)単調性を満たす時、効用関数は(強)単調増加関数となり、無差別曲線は右肩下がりとなる。
$${\because}$$単調性と効用関数の定義より、$${x_i≥y_i⇒u(x)≥u(y)}$$および$${x_i>y_i⇒u(x)>u(y)}$$が成立するが、これは関数の単調増加性に他ならない。また強単調性と効用関数の定義より、$${x≠y}$$かつ$${x_i≥y_i⇒u(x)>u(y)}$$が成立するが、これは関数の強単調増加性に他ならない。また、(強)単調性の定義より、ある消費ベクトル$${x}$$に対し、その右上が上方位集合、左下が下方位集合となるため、無差別な消費ベクトル$${y}$$の軌跡は右肩下がりとなる。
非飽和性と局所非飽和性:消費欲求には限度が無い
選好関係$${≿}$$の非飽和性または局所非飽和性は、直観的にはどちらも「消費欲求には限度が無い」ことを表現している。非飽和性は、どのような消費ベクトルに対しても、それよりも厳密に選好される別の消費ベクトルが存在することを仮定している。例えば、うどん1杯よりも2杯の方がより嬉しいし、2杯より10杯の方がより嬉しいし、10杯よりも…と延々に続いていく。上記は1財のみの比較だが、(強)単調性のように消費ベクトルの各要素が大きい方が好ましい、などの条件はなく、単に「その選択肢よりもいくらでも満足度を上げられる選択肢がある」としか言っておらず、(強)単調性と比較し非常に弱い仮定である。
一方、非飽和性は非常に大域的な仮定であり、例えばうどん$${10^{100}}$$杯のような、現状の選択肢から「かけ離れた」消費ベクトルを考えても問題ないが、分析上の利便性の観点では、現状の選択肢の「近く」でより好ましい選択肢の存在を仮定した方が都合がよく、そこで登場するのが局所非飽和性である。解析的には、現在の選択肢の「近く」を考える際、その点を中心とした半径$${ε>0}$$の開球を考え、その開球内により好ましい選択肢の存在を仮定する。$${ε}$$は任意の正の実数を取れるためいくらでも小さくでき、またそのいくらでも小さな範囲の中にもなお現状より好ましい選択肢の存在を仮定することで、局所非飽和性を表現する(以下の左図)。
消費者を特徴づける選好関係の仮定(2)
非飽和性:任意の消費ベクトル$${x\in X}$$に対して、$${y≻x}$$となる$${y\in X}$$が存在する。
局所非飽和性:任意の消費ベクトル$${x\in X}$$、正の実数$${ε>0}$$に対し、点$${x}$$を中心とする半径$${ε}$$の近傍に$${y≻x}$$となる$${y\in X}$$が存在する。
局所非飽和性と効用関数、無差別曲線の形状
効用関数が定義できる前提のもとで、選好関係$${≿}$$が局所非飽和性を満たす時、効用関数は飽和点を持たず、無差別曲線は厚みを持たない。仮に以下の右図のような厚みを持った無差別曲面を考えると、効用関数の局所非飽和性よりその厚みの中のある消費ベクトル$${x}$$を中心とするいくらでも近傍に$${y≻x}$$となる$${y\in X}$$が存在することになり、これは灰色の領域が無差別であることに矛盾するためである。
なお、局所非飽和性は単調性よりも弱い仮定であり、単調$${⇒}$$局所非飽和が成立する(逆は必ずしも成り立つわけではない)。従って、強単調$${⇒}$$単調$${⇒}$$局所非飽和が成立する。

凸性:多様な財の消費を好む
選好関係$${≿}$$の凸性は、直観的には「単一財の消費よりも多様な財の消費を好む」ことを表現している。例えば、$${x_1=}$$パン、$${x_2=}$$牛乳とした時、2つの消費ベクトル$${x=(100\mathrm{\,g} , 0)}$$、$${y=(0, 50\mathrm{\,g})}$$はそれぞれ、パン100gのみ、牛乳50gのみを消費する選択肢を表す。ここで、例えば$${x:y=6:4}$$で合成した$${0.6x+0.4y=(60\mathrm{\,g}, 20\mathrm{\,g})}$$は、パンを60g食べながら牛乳も20g飲む選択肢であり、パンのみ・牛乳のみを消費する場合よりも好ましいと感じる状況に該当する。
消費者を特徴づける選好関係の仮定(3)
任意の$${x, y\in X}$$、定数$${α\in (0, 1)}$$に対して、
凸性:$${x≿y ⇒ αx+(1-α)y≿y}$$が成り立つ。
狭義凸性:$${x≿y ⇒ αx+(1-α)y≻y}$$が成り立つ。
凸性と効用関数、無差別曲線の形状
効用関数が定義できる前提のもとで、選好関係$${≿}$$が凸性を満たす時、効用関数は準凹関数となり、無差別曲線は原点に対して凸になる。効用関数の準凹性とは以下のように定義されるが、併記した凹性よりも弱い仮定であり、凹性$${⇒}$$準凹性は成り立つが、その逆は必ずしも成り立たない。図形的には以下に示した通り、S字曲線(図の右上)は準凹性が成り立つが凹性は成り立たない例、U字曲線(左下)は準凹性も凹性も成り立たない例である。
効用関数の準凹性
任意の消費ベクトル$${x, y\in X}$$に対して、
$${u(αx+(1-α)y)≥ \min \{ u(x), u(y)\} α\in (0,1)}$$
が成立する。
効用関数の凹性
任意の消費ベクトル$${x, y\in X}$$に対して、
$${u(αx+(1-α)y)≥ αu(x)+(1-α)u(y) α\in (0,1)}$$
が成立する。
選好の凸性$${⇔}$$効用関数の準凹性となるが、これは効用関数の定義$${x≿y⇔u(x)≥u(y)}$$から$${x}$$と$${y}$$の任意の内分点での効用は$${\min \{u(x), u(y)\}=u(y)}$$以上となることが明らかなためである。また、効用関数が凹性を満たす時、$${u(αx+(1-α)y)≥ αu(x)+(1-α)u(y)≥ αu(y)+(1-α)u(y) = u(y) = \min \{u(x), u(y)\}}$$となるため、その効用関数は準凹性も満たす。
効用関数の準凹性より、ある消費ベクトル$${x}$$とその上方位集合に属する別の消費ベクトル$${z}$$との任意の内分点での効用は、やはり元の上方位集合に属することが、以下の右下の図形からも明らかである。このことは、上方位集合が凸集合(へこみのない集合)であることと同値である。従って、選好が凸$${⇔}$$効用関数が準凹$${⇔}$$上方位集合が凸集合、が成り立つ。いずれの性質も図表中の青丸と赤丸、黒丸の位置関係で特徴づけられる。
上方位集合が凸集合
上方位集合$${U=\{y \in X | y≿x\}}$$に属する任意の2点$${p, q}$$に対して、
$${αp+(1-α)q\in U α\in (0,1)}$$
が成り立つ。
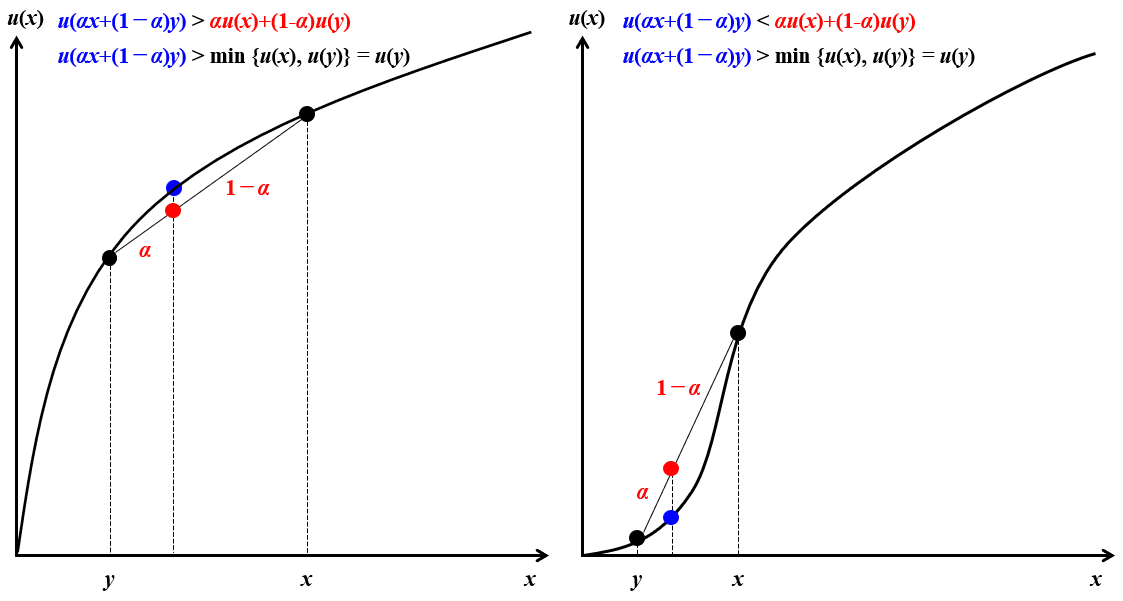

右上:準凹性は満たすが凹性は満たさない効用関数
左下:準凹性も凹性も満たさない効用関数
右下:無差別曲線の凸性。消費ベクトルxとy, zの任意の内分点は上方位集合(灰色の領域)に属する
効用関数と無差別曲線の形状
ここまでの議論をまとめ、選好関係$${≿}$$の標準的な公理系における消費者の性質とそれに対応する選好の性質、効用関数の性質、そして無差別曲線の形状をまとめると以下の通りである。

これら選好関係$${≿}$$の標準的な公理系を全て満たした効用関数と無差別曲線の形状の一例は、以下のように図示される。特定の効用水準を境界に色分けしており、無差別曲線は効用関数の$${x_1-x_2}$$平面への投影図における色分けの境界線に相当しており、上記でまとめた連続性、右肩下がり、厚みを持たない、原点に対して凸、の全ての性質を満たすことが分かる。

以降では、特別な断りが無い限り、選好関係$${≿}$$は標準的な公理系を全て満たすものとして議論を進める。
次回はこちら。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
