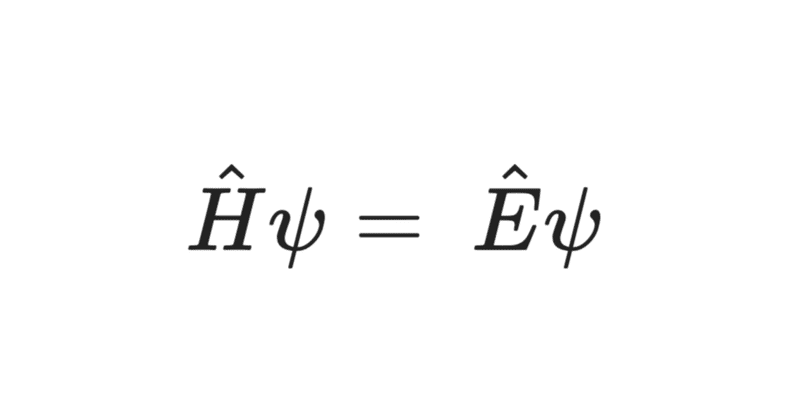
量子力学の入門
今日は数学ではなく、物理をやる。
厨ニ的浪漫の塊、量子力学について。相変わらずざっくりした説明しかしないが許してほしい。
この世界は3次元でできているが本記事では1次元しか扱わない。3次元から入ると微分計算が多すぎて本質的でないところでつまずくと思うからである(大学物理で挫折した人はたぶん物理がわからないのでなく線形代数と微積分で挫折したんじゃないかと思う)。
古典力学の振り返り
粒子の運動
まず、ニュートンの運動方程式
$$
F= ma
$$
物理学の超基本式である。$${F}$$が力、$${m}$$が質量、$${a}$$が加速度である。これは物体に力がかかる時の物体の軌道(位置の変化)を記述する。
次に運動量保存の法則
$$
p = mv
$$
$${p}$$が運動量、$${m}$$が質量、$${v}$$が速度である。ある事象の前後でその系の運動量の総和は変化しない。
最後にエネルギー保存の法則
$$
E = \frac{1}{2} m v^2
$$
これは運動エネルギーだけを書いているが本当はもっとある。系のエネルギーの総和は変化しないということを表す。
ところで、ある物体の位置と速度と加速度はそれぞれ時間をパラメータとした関数であるから
$$
x = x(t)
$$
$$
v = v(t) = \frac{dx}{dt}
$$
$$
a = a(t) = \frac{dv}{dt} = \frac{d^2 x}{dt^2}
$$
である。実は最初に紹介した3つの方程式は全て同じことを言っている。エネルギーを微分すると運動量になって、運動量を微分すると力になる。運動エネルギーは運動量を使うと次のように書ける。
$$
E = \frac{1}{2 m} p^2
$$
この式は後で使う。
波の運動
波動の特徴として次のようなものがある
重ね合わせが起きる
エネルギーは振幅の2乗に比例する
逆にこれらで上手く説明できるものを波動と言って良い(音=空気の振動、はこれに該当する)。それが波であればドップラー効果のような波特有の現象が観測できる。
最も簡単な波を考えよう、特定の一点(位置)における正弦波の波の高さは
$$
A \sin (\omega t + \theta)
$$
これは三角関数の性質から、次の形に変換できる
$$
B \sin (\omega t) + C \cos (\omega t)
$$
要するに正弦波は特定の角周波数 $${ \omega }$$に対して2次元の情報量を持っている(最初の式は$${(A, \theta)}$$、後の式は$${(B, C)}$$である)。2次元情報をエレガントに扱う方法がある、複素数だ。虚数単位$${i}$$を使うと正弦波はこうかける。
$$
A e^{i (\omega t + \theta)}
$$
ここまでは数学の話だが、物理の話に戻す。特定の位置$${x}$$に対する波の高さは波数$${k}$$を使うと
$$
A e^{i (k x - \omega t)}
$$
この時点でついてこれている人がどれだけいるかかなり不安になるが、上の式は正弦波を表しているということだけわかれば良い。
当然、波が正弦波であるとは限らないが、フーリエ変換を使えば全ての波は正弦波の重ね合わせで表現できる。だから正弦波を計算できることが重要で、これができれば他の波は全て計算できる。
光
光がなにかについては歴史的に議論され続けてきた。
光は粒子である
光は波動である
後者を上手く説明したのがヤングの実験である(1800年頃)。その後、光の正体についてはマクスウェル方程式によって電磁波であることが導かれる(1860年頃、またマクスウェル方程式は光速度不変と特殊相対性理論を予言するがここでは扱わない)。
一方、前者の方が上手く説明できてしまう現象が観測される、光電効果、そしてコンプトン効果だ(1840〜1930年頃)。
つまり、光は粒子としての振る舞いと波動としての振る舞いを両方持つ。さらにいうと光だけでなく電子を始めとする小さな粒子(=量子)はすべてこのような振る舞いをしていた。これは観測された現象だからこれを説明できる理論が必要になる、これが量子力学の始まりとなる。
ド・ブロイの式
結論を書くと、粒子の振る舞いと波動の振る舞いをつなぐ式がド・ブロイ波である。まず、量子の運動量は次が成立する。波数$${k}$$とプランク定数$${h}$$を使うと
$$
p = \frac{h}{2 \pi} k = \hbar k
$$
$${\hbar = h / 2 \pi}$$をディラック定数という。計算上便利なのでよく使われる。また、運動エネルギーは次が成立する。周波数$${\nu}$$(角周波数$${\omega}$$に対して
$$
E = h \nu = \hbar \omega
$$
これらは測定された事実だから、素直に信じてほしい。
不確定性原理
物理量の観測には次の限界がある。
$$
\Delta x \Delta p \geq \frac{\hbar}{2}
$$
位置と運動量を同時に精確に観測することはできない(相補性)。これを不確定性原理という。
観測とは「(観測される対象の)量子を(別の観測用の)量子と相互作用することで、その物理量を推定する」行為だから、観測された後に量子の状態が変化することがある。例えば、光子の運動を測るためには別の光子(つまり電磁波)を使うしかないが、別の光子を対象の光子に「ぶつけた」時点で対象の光子の運動量は変化してしまっているはずだ。だから、位置と運動量は同時に測ることができない。
・・というのは古典力学的には観測誤差の限界と解釈できるが、これは量子の本質的な性質であり、量子は不確定性をもつ。量子力学的には観測の限界ではなく、そもそも量子は確率的な振る舞いをする。二重スリットの実験がそれだが、このあたりは後述する。
初等量子力学
ここまで書いたのが高校物理で、ここから大学初年度の物理に入る。疲れてきたがもう少し頑張る。
シュレディンガー方程式
まず次の式を見てほしい。
$$
H(p, x, t) = \frac{1}{2 m} p^2 = E
$$
これはエネルギー保存の法則だが、パラメータを位置、運動量、時間の3つとしている。ここでさらに次の関数を考える
$$
\psi (x, t) = e ^ {i (k x - \omega t)}
$$
正弦波だ。これを位置で微分してみよう
$$
\frac{\partial }{\partial x} \psi = i k e ^ {i (k x - \omega t)} = i k \psi = i \frac{p}{\hbar} \psi
$$
ド・ブロイの式で波数を運動量に変換している。ここで、次の運動量演算子を定義してみる
$$
\hat{p} = -i \hbar \frac{\partial }{\partial x}
$$
明らかに次が成立する(というか成立するように定義した)
$$
\frac{\partial }{\partial x} \psi =\hat{p} \psi
$$
左辺は位置による演算、右辺は運動量による演算で、これらが等価であることを表している。この式を初めて見てなぜ虚数が出てくるのか理解できたら天才だと思うが、数学的には自明である。適当な正弦波を微分するとそれも正弦波になり(sinの微分はcos)、さらに適当に位相をずらすと元の正弦波に一致する(虚数単位を乗じるのは1/4の回転、つまり位相を$${\pi / 2}$$だけ動かすのと等価である)。
これを使いつつ、次のハミルトニアン演算子を考える
$$
\hat{H} = H(\hat{p}, x, t) = \frac{1}{2 m} \hat{p} \hat{p} = - \frac{\hbar^2}{2 m} \frac{\partial^2 }{\partial x^2}
$$
さてもう一方、関数を時間で微分すると
$$
\frac{\partial }{\partial t} \psi = - i \omega e ^ {i (k x - \omega t)} = - i \omega \psi = - i \frac{E}{\hbar} \psi
$$
同じくド・ブロイの式で角周波数をエネルギーに変換している。運動量と同様にエネルギー演算子を考える
$$
\hat{E} = i \hbar \frac{\partial }{\partial t}
$$
さきのハミルトニアン演算子は$${\hat{H} = \hat{E}}$$となるが(意味不明なことを言っているが気持ちで理解してほしい)、これを任意の波動関数$${\psi}$$に対して、
$$
\hat{H} \psi = \hat{E}\psi
$$
これを時間を含むシュレディンガー方程式という。任意の関数はフーリエ変換によって正弦波の重ね合わせで表現できるから、これは関数$${\psi}$$が正弦波でなくても成立する。
ここで、関数$${\psi}$$を空間の関数と時間の関数に分解できると仮定す
る。
$$
{\psi} (x,t) = u(x) T(t)
$$
ちなみに$${\psi}$$が正弦波なら明らかに分解できる(からフーリエ変換を使えば任意の関数に対しても分解できる)。
$$
{\psi} (x,t) = e ^ {i (k x - \omega t}) = e ^ {i k x} e ^ {- i \omega t} = u(x) T(t)
$$
このとき、シュレディンガー方程式は
$$
\hat{H} u T = \hat{E} u T
$$
$${\hat{H}}$$は位置、$${\hat{E}}$$は時間にしか作用せず、それぞれ線形演算子だから計算順序を変えても良い
$$
T \hat{H} u = u \hat{E} T
$$
両辺を$${{\psi} = u T}$$で割ると
$$
\frac{1}{u} \hat{H} u = \frac{1}{T} \hat{E} T
$$
左辺が位置の関数、右辺が時間の関数でこれらが等しいからこれは位置にも時間にも影響を受けない定数で表現できる。定数を$${E}$$とおいて、両辺に$${u}$$を乗じると
$$
\hat{H} u = E u
$$
これを時間を含まないシュレディンガー方程式という。難しそうに見えるが元になっているのはエネルギー保存則とド・ブロイの式だけだ(量子の世界のエネルギー保存則だと思えば良い、時間に関わらず一定のエネルギーを持つという至極当然のことを表している)。
ところで$${\hat{H}}$$は線形演算子だから、これは何らかの線形演算を行ったものがスカラー倍したものと等しくなるということを表す方程式である。すなわち、線形代数における固有値問題である。
$$
E = E_1, E_2, \cdots
$$
これをエネルギー固有値といい、量子のエネルギーは特定の値しか取らないことを示唆する。
波動関数の意味
波動を表した$${\psi}$$は一体なんの意味があるのか。結論として、これは確率密度関数と解釈できる。次の制約条件が必要になる。
$$
\int | \psi(x,t) |^2 dx = 1
$$
つまり、波動関数は量子を波動と考えた場合にはそのまま波動、粒子と考えた場合にはその位置の不確かさを表現する。これは粒子が複数存在するという意味ではなく、粒子は空間上の1点に存在するがそれが観測されるまで、その位置は確率で表現されるという意味である。上の式は「時間を固定した場合、粒子は世界のどこかの1点にある」を意味する。
シュレディンガー方程式を見ればわかるように、方程式を満たす適当な$${\psi_1}$$と$${\psi_2}$$があるならばその線形結合もシュレディンガー方程式を満たす
$$
\psi = c_1 \psi_1 + c_2 \psi_2
$$
さきほどシュレディンガー方程式は固有値問題であると言ったが、エネルギーだけでなくその関数も特定のものしか存在しない(固有関数)。だから、$${\psi}$$を満たすものは
$$
\psi = \psi_1, \psi_2, \cdots
$$
波動関数は固有関数という考え方と、波動関数は確率であるという考え方の整合性をとると次のようになる。量子は特定の系$${\psi_n}$$の重ね合わせの状態で表現され、$${n}$$を選ぶ確率は$${|c_n|^2}$$であり、その観測結果として特定のエネルギー状態 $${E_n}$$ を得る(これを波束の収縮という)。
トンネル効果
エネルギー保存則、というよりハミルトニアンは一般にはポテンシャルを含む。
$$
H(p, x, t) = \frac{1}{2 m} p^2 + V(x)
$$
物体は位置によって影響を受けることがある、高校で学ぶのは重力とか電磁場がこれに相当するが、適当に架空のものを考えても良い。数学は自由だ。例えば、物体が別の物体に衝突する現象を「別の物体と衝突する」ではなく「ポテンシャルがめっちゃ高い空間に進入しようとする」という間接的な捉え方をしても良い。

これを考慮してハミルトニアン演算子を考えると
$$
\hat{H} =- \frac{\hbar^2}{2 m} \frac{\partial^2 }{\partial x^2} + V(x)
$$
・・・。なんにも変わっていないのでは?そのとおり。そもそもハミルトニアン演算子は運動量(つまり速度)をベースに導出していて、ポテンシャルは運動量ではなく位置のみによって物体に影響するなにかを定義しているから、ポテンシャルの部分ははただ単に掛け算するだけである。
次のようなポテンシャルと量子の運動を考えてみる。
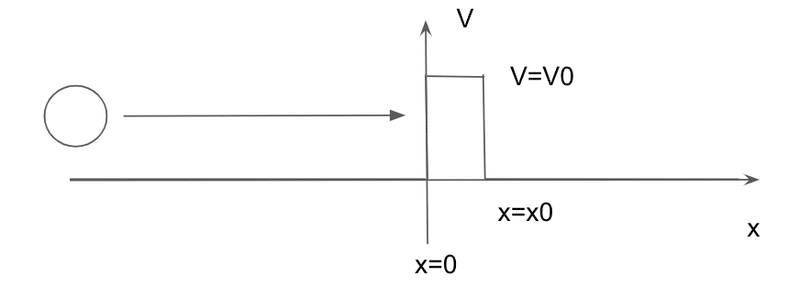
式で書くと
$$
V(x) = V_0 (0 < x < x_0)
$$
イメージとしては左から量子が飛んできて「薄い壁」にぶつかった後どうなるかという感じだ。
量子のエネルギーが$${E > V_0}$$なら、おそらくだが「薄い壁」を突き破って右の方に行くだろう。では、$${E < V_0}$$だとどうなるだろうか。実は壁に阻まれずに右側に行くことがある。これはかなり直感に反する動きだ、エネルギーが足りないはずなのに貫通する。これをトンネル効果という。
量子を波動と考えるとなにかにぶつかったとき透過する波と反射する波に分かれるはずだ。一方、量子は粒子としての性質を持つから分かれるという現象が起こるはずがない。これに整合性を取ると、波動の透過と反射は量子の観測確率として解釈できる。
暇があったらシュレディンガー方程式を解いてほしいが、$${E < V_0}$$のときの透過率を計算するとゼロより大きくなる(これが正しいかどうかは実際に実験し、測定すれば確かめられる)。
おわりに
覚えておくと良いこと
小さな世界では、ものは粒子と波動の二重性をもつ
波動を表現するには三角関数が便利で、三角関数を表現するには複素数が便利である。さらに、粒子と波動の二重性を同時に矛盾なく説明するために確率という概念が役に立つ
「確率的である」を言い換えるとミクロな量子は不確定性をもつともいう。というより本当は逆で、物理現象は本質的に不確定性を持つがマクロに見ると確定的に見える。
数学のnoteをいくつか書いてきたが、高校数学のカリキュラムは良くできているということに気付かされる。
微積分
線形代数(ベクトル、行列)
三角関数
複素数
確率
量子力学に限らず、工学系の分野だと必須の数学知識である。これから勉強する予定の人はきっと役に立つからモチベーション高く学んでほしい。
おまけ;扱わなかったこと
群速度と位相速度
今までほぼ図を書かなかったが、空間を伝わる波は次のような形になっている(だろう)。
波が「まとまっている」部分を波束といいこれが進む速度を群速度という。
$$
v_G = \frac{\partial \omega}{\partial k}
$$
波の「中」の速度を位相速度という。
$$
v_P = \frac{\omega}{k}
$$
ブラケットとオブザーバブル
適当な関数$${\varphi(x,t)}$$、$${\psi(x,t)}$$に対して、内積を次のように書く($${*}$$は共役複素数)。
$$
\braket{\varphi|\psi} = \int \varphi^{*}(x,t) \psi(x,t) dx
$$
波動関数の場合、これを次のように表現することがある。
$${\bra{\varphi}}$$をブラと呼び、検出された状態を表す
$${\ket{\psi}}$$をケットと呼び、準備された状態を表す
初めてこの表記を見たときなにを言っているのか全くわからなかったがそういうものだと思えば良い(数理統計に慣れている人なら事前確率と事後確率みたいなものと思えば良いかもしれない)。
さらに適当な線形演算子$${\hat{A}}$$を使って、次のように書いても良い。
$$
\braket{\varphi|\hat{A} \psi} = \braket{\varphi|\hat{A}|\psi}
$$
できるだけ簡単に説明すると
準備された系を$${\psi}$$として
実験操作によって$${\hat{A}}$$がかかったとき
系$${\varphi}$$を得られる確率が$${\braket{\varphi|\hat{A}|\psi}}$$である
本文の中で実験や観測という単語をかなり曖昧に使ってきたが、本当は数学的に定義しなければならない(例えば、ある系と別のある系を同時に観測できないならそれらの内積はゼロ(=直交)である必要があるはずだ)。
スピン
本文では粒子(あるいは波)が1次元上で直進する場合を考えたが、現実には物体は3次元上で回転できる。つまり、角運動量(あるいはモーメント)も量子力学的に扱う必要がある。
特に電子の角運動量(に相当するもの)をスピンと呼び、その成分は$${\frac{1}{2} \hbar}$$、$${-\frac{1}{2} \hbar}$$のいずれかをもつ。
この記事が気に入ったらサポートをしてみませんか?
