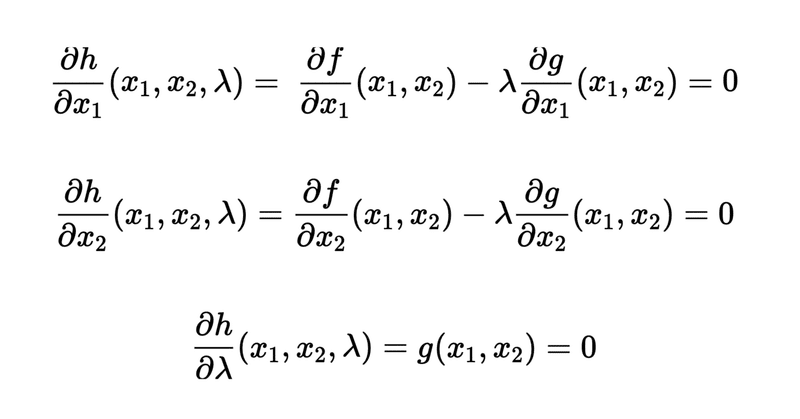
大学1年時に知りたかった微積分

書きすぎた。

微分と積分について簡単に書く。前回と同様にソフトウェアエンジニア向けである。相変わらず厳密なことは考えない。

微分と積分

高校数学のおさらい

微分

微分（differential）とはものすごく小さな変化を求めることである。適当な関数$${f}$$に対して

$$
f’(x) = \frac{df}{dx}(x) \approx \frac{f(x)-f(x+\Delta x)}{\Delta x}
$$

普通は$${\lim}$$とか使うと思うが今日は使わない。

積分

積分（integral）とは小さな変化を足し合わせたものである。

$$
\int f(x) dx \approx \sum \limits_{k} f(x + k \Delta x) \Delta x
$$

積分は微分の逆変換でもある。

極限

極限（limit）の定義はここでは扱わない。わからなくても数学のことは嫌いにならないでほしい。情報系の研究室に6年間いたが1回も使わなかったので実務上は困らないと思う。

なんの役に・・？

何をやってるかは線形代数よりはわかりやすいと思う。何の役に立つかというとこれまた信号処理と数理統計で役に立つ。

微分と積分の式を見るとわかるように、微積分は足したりかけたりする計算である。どこかで聞いたことあるね？微積分は線形近似の計算であり、線形計算の一種である。

偏微分

偏微分（partial derivative）は多変数の関数のときに使われる。2変数の関数$${f(x_2,x_2)}$$に対して、$${x_1}$$で微分するとは

$$
\frac{\partial f}{\partial x_1}(x_1,x_2) \approx \frac{f(x_1,x_2)-f(x_1+\Delta x,x_2)}{\Delta x}
$$

$${x_1}$$の方向の傾きを計算しているとも言える。

数理最適化

最適化（optimization）はある関数の最小値（minimum）を求めたり、最小になるような変数を求めることである。

数理統計（あるいは機械学習）では、誤差を最小化するパラメータを求めるような問題を多く解くことになる。

最適化の基本

微分がゼロになる位置（傾きがゼロの位置）が関数が最小あるいは最大になる位置である。

上の図を見るとわかるように、この方法だと局所最適（local optimum）は求まるが全体最適（global optimum）かはわからない。ただ実用上はこれで良い。

複数の変数があるときはそれぞれの偏微分がゼロになる位置を求める。

$$
\frac{\partial f}{\partial x_1}(x_1,x_2) = 0, \frac{\partial f}{\partial x_2}(x_1,x_2) = 0
$$

ラグランジュの未定乗数法

適当な条件$${g(x_1,x_2)=0}$$のもと、$${f(x_1,x_2)}$$の局所最適を求める。こういうものを制約条件つきの最適化問題と言う。適当な変数$${ \lambda}$$を導入して

$$
h(x_1,x_2,\lambda) = f(x_1,x_2) - \lambda g(x_1,x_2)
$$

これを最適化するとほしいものが手に入る。

$$
\frac{\partial h}{\partial x_1}(x_1,x_2,\lambda) = \frac{\partial f}{\partial x_1}(x_1,x_2) - \lambda \frac{\partial g}{\partial x_1}(x_1,x_2) = 0
$$

$$
\frac{\partial h}{\partial x_2}(x_1,x_2,\lambda) = \frac{\partial f}{\partial x_2}(x_1,x_2) - \lambda \frac{\partial g}{\partial x_2}(x_1,x_2) = 0
$$

$$
\frac{\partial h}{\partial \lambda}(x_1,x_2,\lambda) = g(x_1,x_2) = 0
$$

3つの変数に対して3つの方程式ができるので解が求まる。

例えば、$${f(x,y) = x(y - 1)}$$、ただし$${g(x,y) = x^2 + y^2 - 4 = 0}$$のようなとき、$${h(x,y,\lambda) = f(x,y) - \lambda g(x,y)}$$を考えて

$$
\frac{\partial h}{\partial x} = y - 1 + 2 x \lambda = 0
$$

$$
\frac{\partial h}{\partial y} = x + 2 y \lambda = 0
$$

$$
\frac{\partial h}{\partial \lambda} = x^2 + y^2 - 4 = 0
$$

これくらいだと解析的に解けるが複雑になると解くのが難しくなる。なので、後述する反復解法と組み合わせる。

最急降下法

適当な関数について、最適になる位置を反復的に求めることができる。

$$
x \leftarrow x - \mu f’ (x)
$$

傾きがゼロになる位置をちょっとずつずらして探す。

2次関数の場合

$$
f(x) = a (x - b)^2 + c
$$

$$
f’(x) = 2 a (x - b)
$$

適当な$${x = x_0}$$からはじめて

$$
x_1 \leftarrow x_0 - \mu (2 a (x_0 - b))
$$

$$
x_{n+1} \leftarrow x_n - \mu (2 a (x_n - b))
$$

もし収束すると

$$
x_{\infty} = x_{\infty} - \mu (2 a (x_{\infty} - b))
$$

つまり

$$
x_{\infty} = b
$$

となり、$${x = b}$$のとき局所最適になることがわかる。

ニュートン法

二階微分を使い、反復的に方程式を解く。$${f (x) = 0}$$を解くためには

$$
x \leftarrow x - \frac{f (x)}{f’(x)}
$$

$${f’ (x) = 0}$$を解くためには

$$
x \leftarrow x - \frac{f’ (x)}{f’’(x)}
$$

変数が1個の場合だと割と簡単に式を導出できるが、多変数の場合は二階微分で割る部分が逆行列になるため、簡単に求められないことが多くなる。

2次関数の場合は反復することなく1回で求められる

$$
f’’(x) = 2 a
$$

適当な$${x = x_0}$$からはじめて

$$
x_1 \leftarrow x_0 - \frac{2 a (x_0 - b)}{2a}
$$

つまり

$$
x_1 \leftarrow b
$$

で$${x = b}$$が解である。最急降下法と比べて分かる通り、ステップの係数を上手く取っているという解釈ができる（収束が速い）。

おまけ：一般化逆行列

線形代数の方で、一般化逆行列と最小二乗法は同じと書いた。本当かどうか確かめてみる。

線形回帰

$${(x_k,y_k)}$$が$${n}$$個与えられた時、$${y = ax + b}$$の誤差の二乗を最小化する。

$$
e = \frac{1}{2} \sum \limits_{k} (ax_k + b - y_k)^2
$$

計算しやすくするために$${1/2}$$を乗じている。

$$
\frac{\partial e}{\partial a} = \sum \limits_{k} x_k (ax_k + b - y_k)
$$

$$
\frac{\partial e}{\partial b} = \sum \limits_{k} (ax_k + b - y_k)
$$

これは行列形式で書ける。

$$
\mathbf{E}’ = \begin{bmatrix} \frac{\partial e}{\partial a} \\ \frac{\partial e}{\partial b} \\ \end{bmatrix},\mathbf{A} = \begin{bmatrix} a \\ b \\ \end{bmatrix},\mathbf{X} = \begin{bmatrix} x_1 && 1 \\ \vdots && \vdots \\ x_n && 1 \\ \end{bmatrix}, \mathbf{Y} = \begin{bmatrix} y_1 \\ \vdots \\ y_n \\ \end{bmatrix}
$$

とすると

$$
\mathbf{E}’ = \mathbf{X}^T\mathbf{X}\mathbf{A} - \mathbf{X}^T\mathbf{Y}
$$

これがゼロになるということは？

$$
\mathbf{A} = (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T\mathbf{Y}
$$

$${(\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T}$$は一般化逆行列である。もし$${n=2}$$なら完全な解が求められる（2点を通る直線のパラメータ）。

$${x}$$と$${y}$$はそれぞれ1次元の場合を想定してきたが、それぞれ多次元の場合（多変量解析）でも同じ要領で解ける。というか同じ解き方（一般化逆行列）である。

リッジ回帰

こういう制約条件を付け加えてみる。

$$
a^2 + b^2 = 1
$$

荒っぽく言うとパラメータを安定させるための条件である。これでさっきの線形回帰を考えると

$$
e = \frac{1}{2} \sum \limits_{k} (ax_k + b - y_k)^2 - \frac{\lambda}{2}(a^2 + b^2 - 1)
$$

2ノルムによって制約をかけている形になるが、こういうのをL2正則化（L2 regularization）という。微分すると

$$
\frac{\partial e}{\partial a} = \sum \limits_{k} x_k (ax_k + b - y_k) - \lambda a
$$

$$
\frac{\partial e}{\partial b} = \sum \limits_{k} (ax_k + b - y_k) - \lambda b
$$

行列でまとめると

$$
\mathbf{E}’ = (\mathbf{X}^T\mathbf{X}- \lambda \mathbf{I})\mathbf{A} - \mathbf{X}^T\mathbf{Y}
$$

よって

$$
\mathbf{A} =  (\mathbf{X}^T\mathbf{X}- \lambda \mathbf{I})^{-1} \mathbf{X}^T\mathbf{Y}
$$

厳密には制約条件を満たしているわけではないので、こういうのをソフトな制約と呼ぶことがある。一般化逆行列を用いずに反復的に解きたい場合はこういう風に求める。

$$
\mathbf{A} \leftarrow \mathbf{A} - \mu ((\mathbf{X}^T\mathbf{X}- \lambda \mathbf{I})\mathbf{A} - \mathbf{X}^T\mathbf{Y})
$$

次回

確率編へ