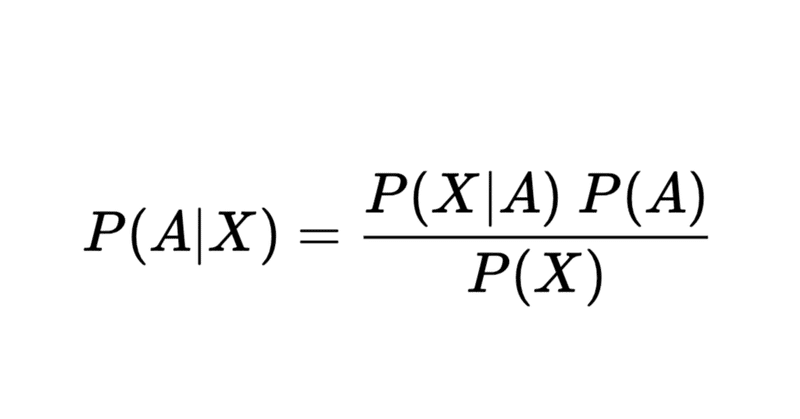
確率と情報と統計の入門

今日も元気に数学ぞい。

今日は数理統計の話。予め断っておくと雰囲気が伝わればまあええやろくらいの記事のため、厳密性はない。

確率

確率

ある事象（event）の起きやすさを確率（probability）という。また、ある変数（確率変数）がある値をとる分布のことを確率分布（probability distribution）といい、その関数を確率密度関数（probability density function）という。

特に有名なものの一つとして、正規分布（normal distribution）の密度関数は

$$
p(x) = \frac{1}{\sqrt{2 \pi}} \exp \left( - \frac{ x^2 }{2}  \right)
$$

また、一様分布（uniform distribution）は

$$
p(x) = \left\{ \begin{array}{ll} 1 & (0 < x < 1) \\ 0  \end{array} \right.
$$

確率は全部足すと（=密度関数を積分すると）1になる（ようにする）。なにが起きるかはわからないがなにかはただ1通りだけ起きる。

サイコロ（1〜6が同じ割合で起きる）を密度関数で表現すると、デルタ関数を使って

$$
p(x) = \displaystyle{ \sum_{k = 1..6} \frac{1}{6} \delta (x - k)}
$$

確率は確率密度の一定区間を部分的に積分したものである。例えば、一様分布で0.5以下が出る確率は

$$
\int_{0}^{0.5} p(x) dx = 0.5
$$

確率変数が連続変数（continuous）だとこうだが、離散（discrete）の場合（例えばサイコロ）は単にこう書く方が便利かもしれない。確率変数$${X}$$がある値$${K}$$を取る確率は

$$
P(X=K) = \frac{1}{6}
$$

これを単にこう書くことがある

$$
P(X) = \frac{1}{6}
$$

横着するとこう書くかもしれない！

$$
p(x) = \frac{1}{6}
$$

$${p}$$とか$${P}$$というのは慣習的なものでこれ自体の表記に特に意味はない。どう見ても違うものだが密度関数と確率をあまり区別しないで書くことがある。連続確率と離散確率の表記上の問題だが、どっちを指しているかは気にした方がいいこともあるし気にしなくていいこともある。本稿はかなり雑なのであまり細かいことは気にしない。

同時確率

ある事象と別のある事象が同時に起きる確率を同時確率（joint probability）といい、その分布を同時分布（joint distribution）という。

独立した確率変数の同時確率はその積になる。そもそも独立とはなんぞやはとりあえず考えない。

$$
P(X,Y) = P(X) P(Y)
$$

これは直感的にはわかる。サイコロを2回振って、同時に「1」が出る確率は1/36である。1回目のサイコロと2回目のサイコロは明らかに独立した事象で全く関係がない。

2つの事象が独立していない場合はこれが成立しない。当たりとはずれが1つずつ入ったくじ引きを1回引いて、くじをもとに戻さずに続けて引くような場合、この2回は独立していない。

条件付き確率

ある事象が起きた状態で、別のある事象が起きる確率を条件付き確率（conditional probability）といい、こう書く。

$$
P(X|Y)P(Y) = P(X,Y)
$$

要するに「Yが起きた状態でXが起きる確率 × Yが起きる確率」と「XとYが同時に起きる確率」は等しい。これは直感的にわかりやすい。

$${X}$$と$${Y}$$が独立している場合は

$$
P(X|Y) = P(X)
$$

これもわかりやすい。逆にこれが成立すればそれぞれの確率変数は独立（independent）であると言える。

事前確率

$${Y}$$と書いてきたものを雰囲気を変えて$${A}$$と書いてみる（特に意味はない）。

$$
P(X|A)P(A) = P(X,A)
$$

$${A}$$が事前の前提として入手できる情報であるとき、これを事前情報（prior information）という。

例えば、スマホのiOSとAndroidのシェアは

• 世界全体だと、3/4がAndroid、1/4くらいがiOS

• 日本だとAndroidとiOSが同じくらい（iOSのほうが少し多い）

「ある人のスマホがiOSである確率は？」この質問は質問した場所が日本なのか中国なのかで前提が変わる。こういうことは多い。

• ある人が風邪をひいている確率

• ある人がプログラミングに詳しい確率

事前情報に係る確率を事前確率（prior probability）という。同時確率を考えると次が成立し、ベイズの定理という。

$$
P(A|X) = \frac{P(X|A) P(A)}{ P(X)}
$$

これを事後確率（posterior probability）といって、起きた結果から逆に情報を推定（estimate）しているとも言える。

よく例に出るスパムメールみたいなのだと

• 全てのメールの中でスパムメールである確率

• スパムメールに特定の文字列が含まれる確率

• メールに特定の文字列が含まれる確率

から「特定の文字列が含まれるメールがスパムメールである確率」を求める、ということができる（こういうのをベイジアンフィルタという）。

観測と推定

サイコロを振って実際に出た値を標本（sample）とか観測値（observed value）といったりする。1個だけ観測してもあまり意味がないので集合で扱う。

$$
\{X_i\} = \{ 1,5,4,3,2,3,4,6,6,3,4,… \}
$$

この観測値から確率分布を推定（estimate）する。

離散分布の場合はわかりやすく「推定された確率 = 起きた事象の数 / 全事象の数」である。実際に観測された値が多いほど、推定された確率は本当の確率に近くなる。

では、連続分布の場合はどうするのか。これは結構難しい。なので、分布の形を決め打ちしてそのパラメータだけを求める。例えば、分布が正規分布と決め打ちして平均と分散だけ求める等、こういうのをパラメトリックな推定（parametric estimation）という。例えば、「歪んだサイコロ」は

$$
p(x) = \displaystyle{ \sum_{k = 1..6} a_k \delta (x - k)}
$$

こう書けるから、$${a_k}$$というパラメータを推定しているといえる。

期待値

適当な関数をかませて分布で加重平均をとったものを期待値（expectation）という。

$$
E[f(x)] = \int f(x) p(x) dx
$$

密度関数で考えるとわかりにくいかもしれない、観測値から推定するやり方のほうがわかりやすい。観測値の集合$${\{x_k\} (k = 1..n)}$$があるとして

$$
E[f(x)] \approx  \frac{1}{n} \sum_k f(x_k)
$$

これ単に平均じゃないの？その通り。$${f(x) = x}$$のとき、これを平均（mean）と呼ぶ。

正規分布

正規分布

次の確率密度関数をもつ分布を正規分布という。

$$
p(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( - \frac{(x - \mu)^2}{ 2 \sigma^2} \right)
$$

この正規分布、数学の色々な世界で出てくる。例えば、最小二乗法は誤差が正規分布に従うという仮定が（実は）ある。

また、正規分布に従う雑音を白色雑音（white noise）という。なぜ正規分布なのか。その一端を少し説明する。

中心極限定理

独立した確率変数を足していくと正規分布に近づく。これを中心極限定理（central limit theorem）という。

なにを言っているのかわからないの思うので具体例を出す。次を計算してみほしい

• サイコロを1回振って、出た目を値とする

  • 目は1,2,3,4,5,6のどれか

• サイコロを2回振って、出た目の和を値とする

  • 目は2,3,3,4,4,4,5,5,5,5,6,6,6,6,6,7,7,7,7,7,7,8,8,8,8,8,9,9,9,9,10,10,10,11,11,12のどれか

• サイコロを3回振って、出た目の和を値とする

• サイコロを4回振って、出た目の和を値とする

• …

2回の時点で分布が「山なり」になっているが、数を増やすとよりなめらかな正規分布になっていく。

これは非常に強力な性質で、この世界の適当な雑音を正規分布と仮定することにかなりの説得力がある。

また、なにを適当に足していっても正規分布に収束することから「正規分布は最も独立という概念から離れた、曖昧で、情報量のない分布」という解釈ができる、これについては後述する。

情報

エントロピー

情報とはなんぞや？確率論的にはこう定義する。

$$
I(x) = - \log p(x)
$$

要するに「起きやすいものは情報量が少ない、起きにくいものは情報量が多い」と考える。これは直感的にわかる。「今日は晴れている」はニュースにならない、「今日は雪が降っている」はニュースになる。

これの期待値を平均情報量あるいはシャノンのエントロピー（entropy）という。

$$
H(x) = E[- \log p(x)] = - \int p(x) \log p(x) dx
$$

ある確率変数が「どれだけの情報をもっているか」を表す。例えば「常に晴れになる」なら天気予報の価値はゼロだ、逆に「晴れと雪の確率がそれぞれ1/2」だったら毎日予報を見る必要がある。

こんなものが一体なんの役に立つのか。たぶん一番役に立つ応用は圧縮（compression）だ。zipとかjpgとかそういうやつだ。圧縮は見かけ上の情報量を実質的な情報量にできるだけ近づける処理のことをいう。毎日予報を見るのではなく、雪が降りそうなときだけ予報を見れば良い、こういうことをデータに対して行う。

相互情報量

2つの確率変数の同時分布に対するエントロピー（結合エントロピー）は

$$
H(x,y) = - \int p(x,y) \log p(x,y) dx dy
$$

もし、$${x}$$と$${y}$$が独立なら対数の恩恵を受けていい感じに分離できる。

$$
H(x,y) = H(x) + H(y)
$$

これは直感的にわかりやすい。独立した2つの情報があって、それぞれの情報を足したら情報量はその和になる。

独立でない時は？情報が「かぶる」、この分を相互情報量（mutual information）という。

$$
I(x;y) = H(x) + H(y) - H(x,y)
$$

ちゃんと書くとこうなる。

$$
I(x;y) = - \int p(x,y) \log \frac{p(x,y)}{p(x)p(y)} dx dy
$$

逆にこれが$${0}$$になることが独立（independent）である。

分布の距離

ある確率変数と別の確率変数が同じ、あるいはどれだけ違うのかはどうやって測ればいいのか。一番リーズナブルなものを一つ紹介する。

$$
D_{KL}(p || q) = \int p(x) \log \frac{p(x)}{q(x)} dx
$$

これをカルバックライブラー情報量（Kullback–Leibler divergence）という（KLダイバージェンスと呼ぶことが多いと思う）。

気づく通り、相互情報量は周辺分布の積と同時分布のKLダイバージェンスである。また、みんな好きかもしれない交差エントロピー（cross entropy）は

$$
H(p, q) = H(p) + D_{KL}(p || q)
$$

こう書ける。

特に重要なのが $${q}$$を正規分布とした時で、logとexpが噛み合っていい感じにまとまる。定数項とスケールを無視すれば、これは平均情報量である。そういう意味で、平均情報量とは正規分布からどれだけ離れた分布なのかを表しているといえる（中心極限定理を思い出そう、混ぜれば混ぜるほど情報がなくなっていく）。

統計

平均

値を全部足して割ったもの、これを平均（mean）という。期待値の形で書くと

$$
\mu = E[x]
$$

である。意味的には中央（center）に近い。

分散

2乗の期待値を分散（variance）という。

$$
\sigma^2 = E[(x - \mu)^2]
$$

その平方根を標準偏差（standard deviation）という。意味的には広がりに近い。

モーメント

確率変数から平均を引いて、標準偏差で割ることを標準化する（standardize）とかいう。こうすると、その確率変数の平均は0、分散は1になり、分布の形（密度関数の形）だけを気にすれば良いことになる。標準化された確率変数のn乗の期待値は

$$
E[x^n]
$$

特に、n=3のものを歪度（skewness）、n=4のものを尖度（kurtosis）と呼ぶ（尖度について、標準正規分布の4次のモーメントは3だから3を引いたものを尖度と呼ぶことがある、ここではあまり区別しない）。歪度は「分布の左右非対称の度合い」、尖度は「裾野の広さ（語源的には尖り具合）」を表す。

一様分布のような「どれもそれなりに均等」だと尖度は低くなり、ラプラス分布のような「多くはゼロに近いがたまに大きな値が出る」だと尖度は高くなる。

多変量と線形代数

変数が2つの場合の2次の統計量を共分散（covariance）という。

$$
C = E[xy]
$$

平均を引いて計算したものを共分散というが、さらに標準偏差で割ったもの（標準化されたもの）を相関（correlation）という。2つの事象がどれだけ「関係しているか」でよく使われるが注意点がある。

• 相関があっても因果関係を説明しない

• 相関がなくても独立とは限らない

因果関係を説明できるのは条件付き分布である、相関は同時分布的な説明しかできない。また独立であるとは、任意のm+n次のモーメント

$$
E[x^m y^n]
$$

がゼロになるのと等価であり、無相関（uncorrelated）はその一部しか説明していない（相互情報量を級数展開できたとして、ある1つの項の係数がゼロ、、というイメージをもつとわかりやすいかもしれない）。

複数の確率変数（確率変数からなるベクトル）の分散と共分散をまとめたものを共分散行列（covariance matrix）という。

$$
\mathbf{C} = [c_{ij}]
$$

ところで、一般に多変量を扱うときベクトルを使うと便利だ。さらに、実際の計算だとサンプルの集合になるので

$$
\mathbf{X} = [x_{ik}]
$$

こんな感じで行列（あるいは2次元配列）の形でまとめる。ここでは行が1つの変数、列がサンプルのインデックスであるとする（逆でもいい）。 サンプルの数は$${n}$$としよう（つまり、$${k = 1…n}$$）。そうすると共分散行列は

$$
\mathbf{C} = \frac{1}{n} \mathbf{X} \mathbf{X}^T
$$

と計算できる。これは対称かつ正定値な行列だから、固有値分解がいい感じに使える。

$$
\mathbf{C} = \mathbf{U} \mathbf{ \Sigma} ^2 \mathbf{U}^T
$$

これを主成分分析（principal component analysis）という。元の多変量を分散の強い順に、分散の強い方向に回転する。

$$
\mathbf{Y} = \mathbf{E}^T \mathbf{X}
$$

「回転する」という表現がよくわからんという人は散布図（scatter plot）を想像してほしい。主成分分析がなにをやっているか見えるはずだ。線形代数は意外と役に立つ。