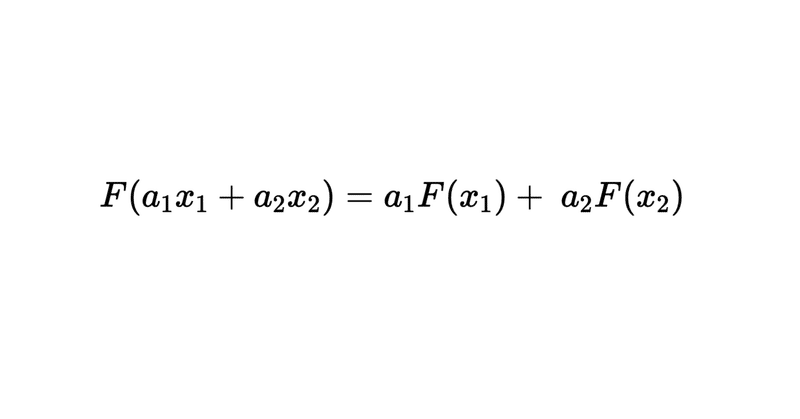
大学1年時に知りたかった線形代数入門
数式が使えるようになったらしい。
線形代数について書いてみる。筆者はCS系の人間なので主にソフトウェアエンジニア向けである。
線形代数で最大の問題は何をやっているのか直感的に全くわからないことと何の役に立つのか全くわからないことだと思う。厳密な定義ではなくなんとなくわかるくらいの粒度にしてあるので諸々容赦願いたい。
線形演算
なんらかの処理$${F}$$について
$$
F(a_1 x_1 + a_2 x_2) = a_1 F(x_1) + a_2 F(x_2)
$$
が成立する時、$${F}$$を線形変換という。要するに処理を後から適用しても、先に適用しても結果が同じになることを言う。これだとだとなんのこっちゃという感じだと思うので例を出す。
行列計算
行列計算(行列の乗算)は線形変換である。
$$
\mathbf{B} (a_1 \mathbf{x_1} + a_2\mathbf{x_2}) = a_1 \mathbf{B} \mathbf{x_1} + a_2 \mathbf{B} \mathbf{x_2}
$$
逆に、線形変換の性質をもつものは行列計算で表現できる。というより線形の計算の表現の仕方の一つが行列である(全部同じことを言っている)。
行列計算を忘れている人のために一応書いておく。変数が2次元だと
$$
\mathbf{A}\mathbf{x} = \begin{bmatrix} a_{11} && a_{12} \\ a_{21} && a_{22} \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} a_{11} x_{1} + a_{12} x_{2} \\ a_{21} x_{1} + a_{22} x_{2} \end{bmatrix}
$$
行列は縦ベクトルが横に並んでいると解釈すると、これはこういう風に書いても良い。
$$
\mathbf{A}\mathbf{x} = \begin{bmatrix} \mathbf{a}_{1} && \mathbf{a}_{2} \\ \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \mathbf{a}_{1} x_{1} + \mathbf{a}_{2} x_{2}
$$
横ベクトルが縦に並んでいると解釈してもよく、こういう風にも書ける。
$$
\mathbf{A}\mathbf{x} = \begin{bmatrix} \mathbf{\bar{a}}_{1}^T \\ \mathbf{\bar{a}}_{2}^T \\ \end{bmatrix} \mathbf{x} = \begin{bmatrix} \mathbf{\bar{a}}_{1}^T\mathbf{x} \\ \mathbf{\bar{a}}_{2}^T\mathbf{x} \\ \end{bmatrix}
$$
なんの役に・・?
行列計算がなんの役に立つかというと信号処理と数理統計で良く使われる。特に機械学習の領域だとたくさん出てくるので知っておくと役に立つかもしれない。また、多くの自然現象はミクロに見たりあるいは遠目に見たりすると線形近似できる(ことがある)。線形を制すものは自然を制す。
なんの意味が・・?
ここでは4通りの考え方を紹介する。初見で全部理解するのは無理なので1個くらいわかるものが見つかれば良いと思う。
$$
\mathbf{y} = \begin{bmatrix} y_{1} \\ y_{2} \\ \end{bmatrix} = \mathbf{A}\mathbf{x} = \begin{bmatrix} a_{11} && a_{12} \\ a_{21} && a_{22} \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}
$$
1つ目、信号処理的な考え方その1。$${\mathbf{A}}$$を線形フィルタと考える。例えば
$$
\mathbf{A} = \begin{bmatrix} 1/2 && 1/2 \\ -1 && 1 \end{bmatrix}
$$
こうすると
$$
y_1 = \frac{x_1 + x_2}{2}
$$
$$
y_2 =- x_1 + x_2
$$
こうなるので前者は平均、後者は差分を抜き出していると考えられる。
2つ目、信号処理的な考え方その2。$${x_1(t)}$$と$${x_2(t)}$$が時間的な入力信号であり、$${y_1(t)}$$と$${y_2(t)}$$がこれらの出力信号とするとこれは線形システムである。
例えば、適当な$${x_1(t)}$$と$${x_2(t)}$$があって
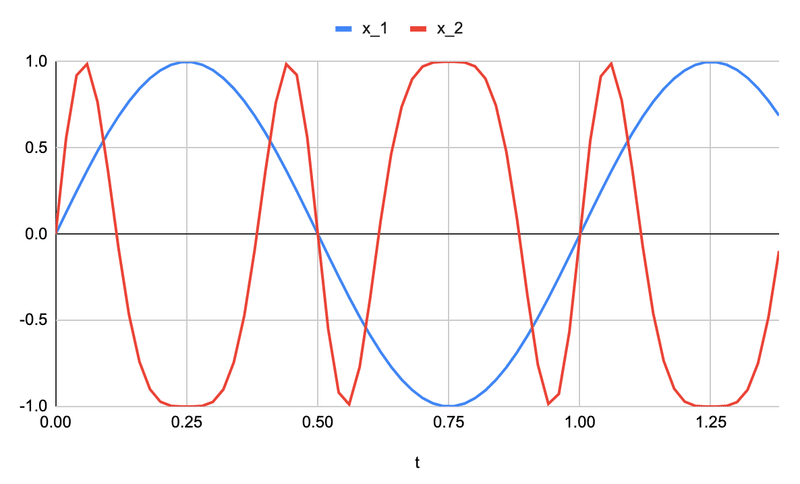
$${a_{11}=0.5}$$、$${a_{12}=0.1}$$、$${a_{21}=0.2}$$、$${{a_{22}}=-0.7}$$を適用すると

こうなる。
3つ目、統計的あるいは幾何的な考え方。$${x_1}$$と$${x_2}$$を確率変数とみなす。すると$${y_1}$$と$${y_2}$$も確率変数だが、このときの散布図は
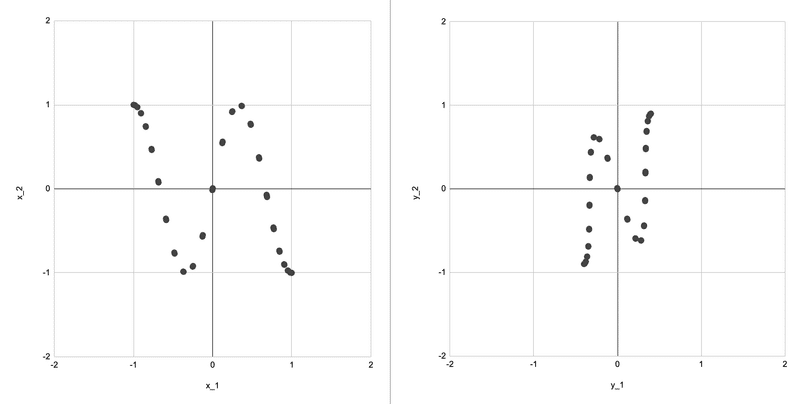
横に縮めて反転させたようになる。言い換えると分布を変形させている。
4つ目、基底の変換。まず次のような行列を考える。
$$
\mathbf{I} = \begin{bmatrix} 1 && 0 \\ 0 && 1 \\ \end{bmatrix} = \begin{bmatrix} \mathbf{i}_1 && \mathbf{i}_2 \\ \end{bmatrix}
$$
これは単位行列と呼ばれるものだがこれを使うと$${\mathbf{x}}$$はこう表現できる。
$$
\mathbf{x} = \mathbf{I}\mathbf{x} = \mathbf{i}_{1} x_{1} + \mathbf{i}_{2} x_{2}
$$
これは$${\mathbf{x}}$$を2つのベクトル$${\mathbf{i}_{1}}$$と$${\mathbf{i}_{2}}$$の線形結合で表現していると解釈できる。 続いて、$${\mathbf{A}}$$の逆行列$${\mathbf{B}=\mathbf{A}^{-1}}$$を考える。
$$
\mathbf{x} = \mathbf{B}\mathbf{y} = \mathbf{b}_{1} y_{1} + \mathbf{b}_{2} y_{2}
$$
これは$${\mathbf{x}}$$を単位ベクトルではない2つのベクトル$${\mathbf{b}_{1}}$$と$${\mathbf{b}_{2}}$$の線形結合で表現していると解釈できる。このように基底ベクトルを変えることができる。
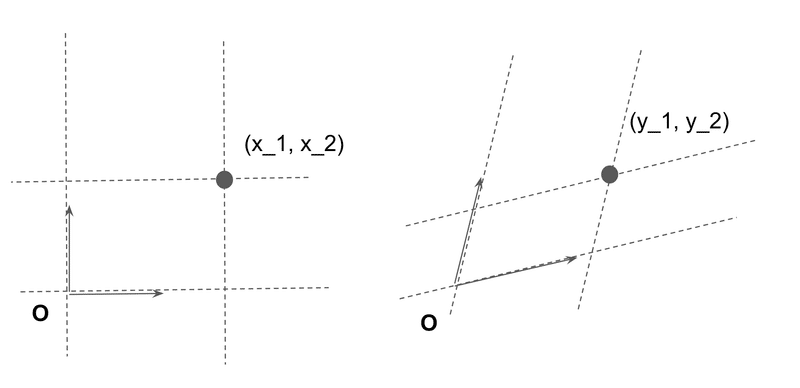
線形な座標とは、2本のまっすぐな定規を縦と横において測ることである。さっきの散布図は定規(=測り方)を変えずに位置を変化させたと言えるし、こちらは位置を変えずに尺度の違う定規を斜めに置いて測ったものとも言える。どちらも同じことを言っている、別の解釈をしているだけである。
最後に行列のランクにふれる。次元が$${2 \times 2}$$の行列のランクはだいたい$${2}$$である(粗い説明)。ランクが$${1}$$になるときはこういうとき
$$
\mathbf{A} = \begin{bmatrix} 1 && 1 \\ 2 && 2 \end{bmatrix}
$$
このとき、$${y_1 = x_1 + x_2}$$、$${y_2 = 2 (x_1 + x_2) = 2 y_1}$$。もともと$${2}$$次元あった情報が実質的に$${1}$$次元になる。しかも元に戻せない(逆行列が存在しないという言い方もできる)。
このときにさっきの図はどうなるかというと
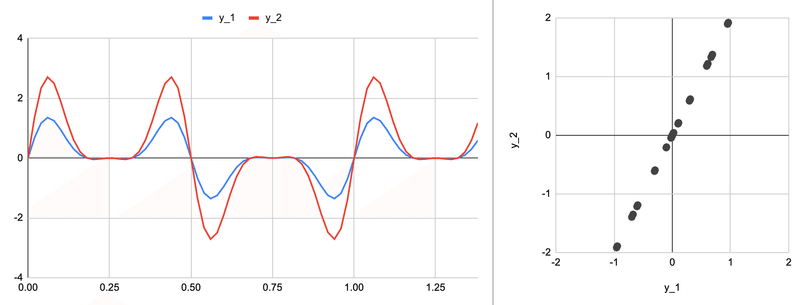
明らかに$${1}$$次元分の情報量しかない。この状態は基底が1次独立でないとも言える(2つの基底が同じ方向を向いていて区別できない)。また、ランクが$${0}$$とは
$$
\mathbf{A} = \begin{bmatrix} 0 && 0 \\ 0 && 0 \end{bmatrix}
$$
このとき、$${y_1 = y_2 = 0}$$で$${x_1}$$と$${x_2}$$は完全に消えて情報量ゼロになる。
特異値分解
行列の分解で個人的に一番大事だと思うのが特異値分解(singular value decomposition)だと思うのでこれの説明をする。が、その前に直交行列と対角行列の説明をする。
直交行列
直交行列(orthogonal matrix)はその転置行列が逆行列になる行列のことをいう。
$$
\mathbf{A} \mathbf{A}^T = \mathbf{I}
$$
直交行列は各列ベクトルが互いに直交する(内積がゼロになる)。
$$
\mathbf{a}_{ij}^T \mathbf{a}_{ij} = 0 (i \neq j)
$$
これは幾何学的には点を原点を中心に回転させる処理である。2次元の場合は複素数平面と同じなので、適当な回転角$${\theta}$$を使って
$$
\mathbf{A} = \begin{bmatrix} \cos(\theta) && -\sin(\theta) \\ \sin(\theta)&& \cos(\theta) \\ \end{bmatrix}
$$
こう表現できる。
対角行列
対角行列(diagonal matrix)は対角成分以外がゼロである行列のことをいう。
$$
\mathbf{A} = \begin{bmatrix} a_1 && \cdots && 0 \\ \vdots && \ddots && \vdots \\ 0 && \cdots && a_n \\ \end{bmatrix}
$$
対角行列も直交行列と同様に逆行列を簡単に計算できる。対角成分の逆数を取るだけで良い。幾何学的にはスカラー倍(拡大・縮小)の処理である。2次元の場合には
$$
\mathbf{A} = \begin{bmatrix} a_1 && 0 \\ 0&& a_2 \end{bmatrix}
$$
だから
$$
y_1 = a_1 x_1
$$
$$
y_2 = a_2 x_2
$$
となる。
特異値分解
任意の行列$${\mathbf{A}}$$は次のように分解できる
$$
\mathbf{A} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^T
$$
$${\mathbf{U}}$$と$${\mathbf{V}}$$は直交行列、$${\mathbf{\Sigma}}$$は成分が非負の対角行列である。これはベクトルに行列を乗じるという処理が、回転して、縦横に引き伸ばして、また回転する、という処理であることを意味する。線形変換とはこういう処理なのである。逆にこれ以上のことはできない(アフィン変換を知っている人はそれを想像すると良い)。
直交行列と対角行列は逆行列を簡単に求められるので、特異値分解した後はその逆行列を簡単に求められる。
$$
\mathbf{A}^{-1} = \mathbf{V}\mathbf{\Sigma^{-1}}\mathbf{U}^T
$$
正定値対称行列
固有値分解(eigen value decomposition)をしたときに、固有値が実数かつ正になるような対称行列のことを正定値対称行列(positive definite)という。固有値がゼロまたは正の場合は半正定値対称行列(semi-positive definite)ともいう。なんのこっちゃ。
定義だけ聞くと意味不明なので具体的な行列の方が重要である。任意の行列$${\mathbf{A}}$$に対して、次の行列は半正定値対称行列になる。
$$
\mathbf{B} = \mathbf{A}\mathbf{A}^T
$$
これも半正定値対称行列になる。
$$
\mathbf{G} = \mathbf{A}^T\mathbf{A}
$$
これはグラム行列という。数理統計あるいは機械学習の領域だと共分散行列(covariance matrix)がこれと同じ計算をする。
これの固有値が正定値になることは特異値分解を考えればわかる。
$$
\mathbf{A}\mathbf{A}^T = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^T (\mathbf{U}\mathbf{\Sigma}\mathbf{V}^T)^T = \mathbf{U}\mathbf{\Sigma^2}\mathbf{U}^T
$$
特異値の二乗が固有値になる(つまり固有値は非負の実数になる)。また逆に、正定値対称行列の固有値分解を解けるなら特異値分解も解ける。固有値分解の時点で$${\mathbf{U}}$$と$${\mathbf{\Sigma}}$$はわかっているから
$$
\mathbf{V}^T = \mathbf{U} \mathbf{\Sigma}^{-1}\mathbf{A}
$$
解き方としては、ヤコビ法のようなリーズナブルな解法がある。
逆行列
いままでなんのなしに逆行列(inverse)と言ってきた。定義は
$$
\mathbf{A} \mathbf{A}^{-1} = \mathbf{I}
$$
連立1次方程式
逆行列を求めることは、連立1次方程式を解くことと同じである。
$$
\mathbf{A}\mathbf{x} = \mathbf{b}
$$
に対して
$$
\mathbf{x} = \mathbf{A}^{-1}\mathbf{b}
$$
一般化逆行列
逆行列は正方行列かつfull rankな行列しか扱えないが、非正方行列かつfull rankでない行列にも拡張することができる。これを一般化逆行列(generalized inverse)あるいは疑似逆行列という。$${\mathbf{A}}$$が$${m \times n}$$の行列で$${rank(A)=k}$$とすると、特異値分解から
$$
\mathbf{A}^{-1} = \mathbf{V}\mathbf{\Sigma^{-1}}\mathbf{U}^T
$$
ただし、$${\mathbf{\Sigma^{-1}}}$$は$${n \times m}$$の行列で対角成分が$${1 / \sigma_1,\cdots,1/\sigma_k,0,\cdots,0}$$である。
最小二乗法
一般化逆行列がなにに使えるとかと言うと、これは最小二乗法と同じである。なんのこっちゃ。
適当な$${(x_k,y_k)}$$の組が$${n}$$個与えられたときに、いい感じの$${a}$$と$${b}$$を求める。
$$
y \approx a x + b
$$
この「いい感じ」について、誤差の二乗の総和を最小にするのが最小二乗法である。これは一般化逆行列の問題として解ける。
$$
\begin{bmatrix} x_1 && 1 \\ \vdots && \vdots \\ x_n && 1 \\ \end{bmatrix} \begin{bmatrix} a \\ b \\ \end{bmatrix} = \begin{bmatrix} y_1 \\ \vdots \\ y_n \\ \end{bmatrix}
$$
つまり
$$
\begin{bmatrix} a \\ b \\ \end{bmatrix} = \begin{bmatrix} x_1 && 1 \\ \vdots && \vdots \\ x_n && 1 \\ \end{bmatrix}^{-1} \begin{bmatrix} y_1 \\ \vdots \\ y_n \\ \end{bmatrix}
$$
ちなみにこれは正規分布のノイズを加えた確率過程とも解釈でき
$$
y = a x + b + n
$$
荒っぽく言って以下は全部同じような計算をしている。
特異値分解
一般化逆行列
最小二乗法
主成分分析
多次元尺度構成法(ユークリッド距離を使った場合)
線形回帰(回帰分析)
フィッシャーの線形判別
おまけ:離散コサイン変換
ソフトウェアエンジニア的に特に重要なものを一つだけ紹介しておく。直交変換のひとつ、離散コサイン変換(DCT; discrete cosine transform)だ。これがわかればjpegやmp3の原理を理解できる。
オーディオや映像などのメディア情報は大雑把に言って2種類の処理によって情報を圧縮する。
データに偏りをもたせる
偏ったデータは圧縮できる
DCTは前者に使う。後者でわかりやすいのはハフマン符号化とか。画像やオーディオの信号は短期的に見ると周期的であり、特に低周波成分にエネルギーが集中する。
ちなみに機械学習のような特徴抽出(feature extraction)では高周波成分やエッジの方が重要である(圧縮できない部分=特徴)。

DCTの解説までしようと思ったが力尽きてしまった。適当にググってほしい(すまん)。
自分はこういう順に勉強した覚えがある。フーリエ級数展開→フーリエ変換(→ラプラス変換)→離散フーリエ変換(→高速フーリエ変換)→離散コサイン変換。人によっては逆順に教えたほうがいいんじゃないかと思ってフーリエ変換を飛ばしてDCTの説明をしてみたのだ。
次回
微積分へ
この記事が気に入ったらサポートをしてみませんか?
