
【難関】モーリーの定理の証明-アラン・コンヌによる代数的証明-
こんにちは。和からの数学講師の岡本です。以前、モーリーの定理を紹介し、三角比を使った証明を解説しました。今回は1982年に“数学界のノーベル賞”とも言われるフィールズ賞を受賞した天才数学者アラン・コンヌによる「代数的な別証明」の概説をしていこうと思います。(※もちろんですが、モーリーの定理の別証明がフィールズ賞受賞理由ではありません。)
なお、コンヌによる証明は以下のURLから読むことができます。きちんと内容を理解したい方はこちらをご覧ください!
この記事の主な内容
1.モーリーの定理(再掲)
2.不動点という視点
3.コンヌの定理とモーリーの定理
4.さいごに
1.モーリーの定理(再掲)
ひとまず、モーリーの定理の主張を述べます(詳しくは過去のマスログをご覧ください)
定理(フランク・モーリー,1899)
任意の三角形の各頂点から、角の3等分線を伸ばす。
2つの頂点の隣り合う3等分線の交点を結ぶと正三角形ができる。
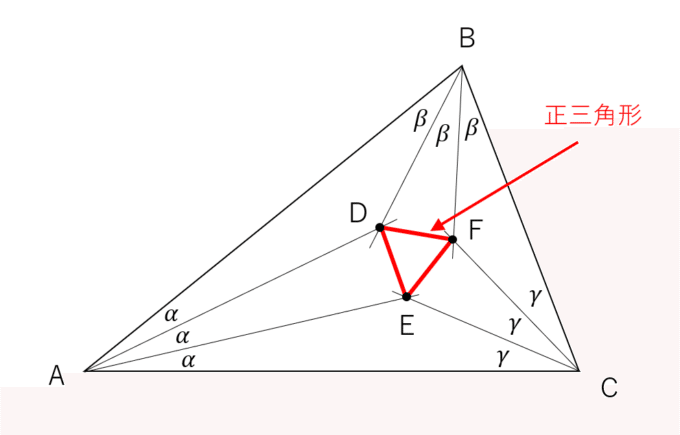
いやー!何度見ても美しいですね!!
このシンプルな結論の美しさにコンヌも魅了され、証明を一生懸命考えたのでしょう。
2.不動点という視点
例のように各頂点から3等分線を引きます。こうしてできた「交点」をコンヌは「ある変換の不動点」と考えました。なかなか思いつかない発想ですよね…!
ここでいう変換というのは「回転」や「平行移動」、またそれらの組み合わせを意味します(「運動」と表現するとわかり易いかもしれません)。
続きはこちらから!
この記事が気に入ったらサポートをしてみませんか?
