<学習シリーズ>線形モデル編:多項式回帰/非線形回帰
1.概要
1-1.緒言
本記事は”学習シリーズ”として自分の勉強備忘録用になります。
過去の記事で機械学習・AIの記事を多数作成しましたが、シンプルな線形モデルは外挿が比較的得意のためいろんな分野で使用されます。
本記事では「多項式回帰」を学習します。
1-2.用語・記号の説明(全般)
本記事で使用する用語および記号は下記の通りです。
1-2-1.用語一覧
●回帰 (regression):実数値を予測する問題
●分類 (classification):カテゴリ(離散値)を予測する問題
●教師あり学習 (supervised learning):機械学習でデータセットに対して正解値(ラベル)がある学習方法
●教師なし学習 (unsupervised learning):機械学習でデータセットに対して正解値(ラベル)が無い学習方法
●予測値 (predicted value):関数で計算された出力変数y(用語は下記参照)
●目標値 (target value):予測値がとるべき値(教師あり学習の正解値)
●目的関数 (objective function):機械学習において性能の良さの指標を表す関数です。一般的には”予想値と目標値の差異”から作成される関数であり、この関数を最小化することでよいモデルと判断します。
●多重共線性(multicollinearity):多変量解析(重回帰分析など)において、いくつかの説明変数間で線形関係(強い相関関係)があると共線性といい、共線性が複数認められる場合は多重共線性があると言います。
●二乗和誤差 (sum-of-squares error):正解値$${y}$$と予測値$${\hat{y}}$$の差の2乗$${(y-\hat{y})^2}$$です。これをモデルと正解値の誤差とも呼びます。
●最小二乗法:二乗和誤差を最小化することでモデルの当てはまりを最適化する手法です。
1-2-2.記号一覧
●$${f()}$$:$${y=f(x)}$$におけるf()であり関数と呼びます。中身は入力変数xを処理して新しい出力変数yを生成する計算式です。
●$${x}$$:$${y=f(x)}$$におけるxです。複数は下記の通り複数あります。
名称1:説明変数(Explanatory variable)
名称2:独立変数(Independent variable)
名称3:外生変数(Exogenous variable)
名称4:入力変数(Input variable)
名称5:入力値(Input value)
●$${y}$$:$${y=f(x)}$$におけるyです。複数は下記の通り複数あります。
名称1:目的変数(Response variable)
名称2:従属変数(Dependent variable)
名称3:被説明変数(Explained variable)
名称4:内生変数(endogenous variable)
名称5:出力変数(Output variable)
名称6:予測値/推論値(prediction value)
●$${w_i}$$(weight):重み(単回帰の場合は傾きとも言う)
●$${b}$$(bias):バイアス(単回帰の場合は切片とも言う)
1-2-3.ベクトル・行列表記一覧
●M次元の縦ベクトル:$${{\bf x}}$$
$$
\begin{aligned}{\bf x}= \begin{bmatrix} x_{0} \\ x_{1}\\ x_{2} \\ \vdots \\ x_{M} \end{bmatrix} \\ \end{aligned}
$$
●M次元の横ベクトル(縦ベクトルの転置):$${{\bf x}^{\rm T}}$$
$$
\begin{aligned}{\bf x}^{\rm T}= \begin{bmatrix} x_{0} & x_{1}& x_{2} & \dots & x_{M} \end{bmatrix} & \end{aligned}
$$
●N×M次元の行列(M次元をもつN個のデータ):$${{\bf X}}$$
$$
\begin{aligned}
{\bf X} &
= \begin{bmatrix} x_{10} & x_{11} & x_{12} & \cdots & x_{1M} \\
x_{20} & x_{21} & x_{22} & \cdots & x_{2M} \\
x_{30} & x_{31} & x_{32} & \cdots & x_{3M} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\ x_{N0} & x_{N1} & x_{N2} & \cdots & x_{NM} \end{bmatrix}
\end{aligned}
=\begin{bmatrix} {\bf x}_1^{\rm T} \\ {\bf x}_2^{\rm T} \\ {\bf x}_3^{\rm T}\\ \vdots \\ {\bf x}_N^{\rm T} \end{bmatrix}
$$
1-3.サンプル用データ
サンプルデータはScikit-learnの「sklearn.datasets.make_moons」を使用しました。本データセットはもともとクラスタリング用のデータセットとなります。よって説明変数が2次元データで目的変数がクラス番号となります。
[IN]
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
from mpl_toolkits.mplot3d import Axes3D
from sklearn import datasets
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from tqdm import tqdm
from typing import Tuple, List, Dict, Union, Any, Optional
import os
import glob
#フォルダ作成
if not os.path.exists('output'):
os.makedirs('output')
#サンプルデータ取得
data_moons = datasets.make_moons(n_samples=30, noise=0.09, random_state=0)
X, Y = data_moons
print(f'データの形状 X:{X.shape}、Y:{Y.shape}')
df_origin = pd.DataFrame(np.concatenate([X, Y.reshape(-1, 1)], axis=1), columns=['x1', 'x2', 'y'])
display(df_origin.head())
sns.scatterplot(x='x1', y='x2', data=df_origin, hue='y', style='y')
plt.show()
[OUT]
データの形状 X:(30, 2)、Y:(30,)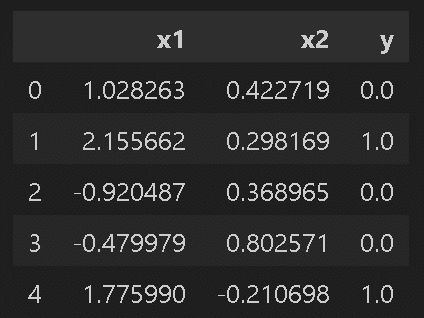

非線形のデータなら何でもよかったので、クラス番号は除去して説明変数の$${x_{1}=x}$$, $${x_{2}=y}$$として2次元データに変換して使用します。
図を見てわかる通り直線では絶対うまくフィットしないデータです。
[IN]
#2次元データとして抽出
df = df_origin[['x1', 'x2']].rename(columns={'x1': 'x', 'x2': 'y'})
print(f'データの形状:{df.shape}')
display(df.head())
sns.scatterplot(x='x', y='y', data=df)
plt.show()
[OUT]
データの形状:(30, 2)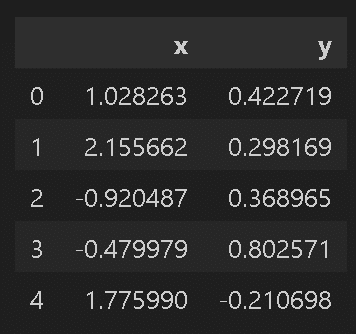

2.基礎知識
2-1.重み付き和
重み付き和とは係数をかけてつくられる和のことであり,加重和や線形和などともよばれます。
例えば5教科の点数で6人の生徒を評価します。単純な手法としては、各教科の点数を$${x_{i}}$$として合計を計算します。
$$
\begin{aligned}
評価点(単純和) &=\sum_{i}^{5}x_{i} \\&=\bf w^T \bf x
\\&=\begin{bmatrix} 1 & 1 & 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} x_{国語} \\ x_{数学} \\ x_{英語} \\ x_{社会} \\ x_{理科} \end{bmatrix}
\end{aligned}
$$
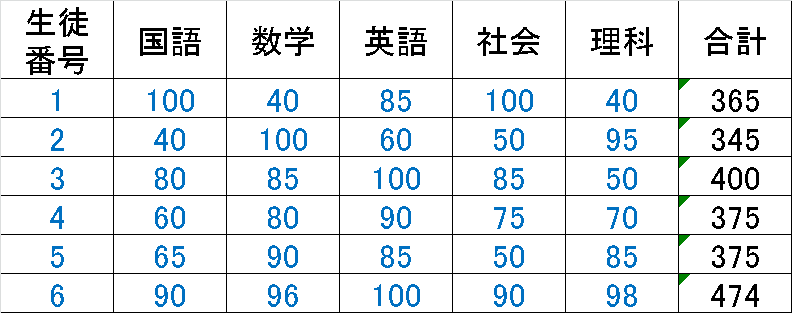
重み付き和は各要素に重みをかけて足し合わせます。例えば、教科ごとに異なる重要性を考慮する場合に、点数に重みをかけることができます。今回は数学、英語、理科に重きを置いて計算しました。これにより評価点の順位が変わっていることが確認できます。
後述しますが、「$${\sum_{i}^{n}w_{i}x_{i} =\bf w^T \bf x }$$より重回帰と同じ」であり「関数同士の重み付き和をとることにより重要な関数の特徴を考慮した合成関数を作成することが可能」となります。
$$
\begin{aligned}
評価点(加重和) &=\sum_{i}^{5}w_{i}x_{i} =\bf w^T \bf x
\\&=\begin{bmatrix} w_{1} & w_{2} & w_{3} & w_{4} & w_{5} \end{bmatrix} \begin{bmatrix} x_{国語} \\ x_{数学} \\ x_{英語} \\ x_{社会} \\ x_{理科} \end{bmatrix}
\\&= w_{1}x_{国語} + w_{2}x_{数学} + w_{3}x_{英語} + w_{4}x_{社会} + w_{5}x_{理科}
\end{aligned}
$$


2-2.単回帰・重回帰
2-2-1.単回帰の数式
単回帰は重回帰における説明変数が1次元のものになります($${x_0=1}$$)。
$$
単回帰:y = w_{1}x_{1} +w_{0}=\begin{bmatrix} w_{0}&w_{1}\end{bmatrix} \begin{bmatrix} x_{0} \\ x_{1} \end{bmatrix}=\bf w^Tx
$$
2-2-2.重回帰の数式
重回帰は各説明変数に重みをかけた値の総和+バイアス項です。
$$
重回帰:y = w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + b=\sum_{m=1}^{M} w_{m} x_{m} + b
$$
M次元の入力変数$${x}$$に$${x_0=1}$$を追加してM+1次元とし、同様にM次元の重み$${w}$$に$${w_0=b}$$を追加すると下記へ変換できます。
$$
\begin{aligned} y &
= w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + b \\ &
= w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + w_{0}x_{0} \\ &
= w_{0}x_{0} + w_{1}x_{1} + \cdots + w_{M}x_{M} \\ &
= \sum_{m=0}^M w_{m} x_{m} \end{aligned}
$$
2-2-3.重回帰を行列に変換
重回帰は多次元のためベクトル・行列で表され、直接解法も行列で計算するため行列式で表現する方が便利となります。
重回帰を重み$${\bf w}$$と説明変数$${\bf x}$$のベクトルの内積で表現するることができます。なお注意点は下記の通りです。
バイアス$${b}$$は$${x_0=1}$$, $${w_0=b}$$より$${w_0x_0=b}$$で存在
バイアス$${b}$$を含むため$${\bf w}$$, $${\bf x}$$共にM+1次元
ベクトル同士の内積を計算するために、重み$${\bf w}$$は転置
【データ数が1個(1行の行列):1×(M+1)行列】
$$
\begin{aligned} y = w_{0}x_{0} + w_{1}x_{1} + \cdots + w_{M}x_{M} = \begin{bmatrix} w_{0} & w_{1} & \cdots & w_{M} \end{bmatrix} \begin{bmatrix} x_{0} \\ x_{1} \\ \vdots \\ x_{M} \end{bmatrix} = {\bf w}^{\rm T}{\bf x}
\end{aligned}
$$
【データ数がN個(N行の行列):(N×(M+1)行列)】
$$
\begin{aligned}{\bf y}&
=\begin{bmatrix} y_1 \\ y_2 \\y_3 \\ \vdots \\ y_N \end{bmatrix}
=\begin{bmatrix}{\bf x}_1^{\rm T}{\bf w} \\{\bf x}_2^{\rm T}{\bf w} \\{\bf x}_3^{\rm T}{\bf w} \\\vdots \\{\bf x}_N^{\rm T}{\bf w}\end{bmatrix}
= \begin{bmatrix}w_{10}x_{10} + w_{11}x_{11} + w_{12}x_{12} + \cdots + w_{1M}x_{1M} \\w_{20}x_{20} + w_{21}x_{21} + w_{22}x_{22} + \cdots + w_{2M}x_{2M} \\ w_{30}x_{30} + w_{31}x_{31} + w_{32}x_{32} + \cdots + w_{3M}x_{3M} \\
\vdots
\\w_{N0}x_{N0} + w_{N1}x_{N1} + w_{N2}x_{N2} + \cdots + w_{NM}x_{NM}\end{bmatrix}\end{aligned}
$$
$$
=\begin{bmatrix}x_{10} & x_{11} & x_{12} & \cdots & x_{1M} \\
x_{20} & x_{21} & x_{22} & \cdots & x_{2M} \\
x_{30} & x_{31} & x_{32} & \cdots & x_{3M} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{N0} & x_{N1} & x_{N2} & \cdots & x_{NM}\end{bmatrix}
\begin{bmatrix}w_{0} \\w_{1} \\w_{2} \\\vdots \\w_{M}\end{bmatrix}
= {\bf X}{\bf w}
$$
2-3.交互作用特徴量:PolynomialFeatures
交互作用特徴量は特徴量作成(前処理)技術の一つであり、各次元をかけ合わせることで新しい次元を作成しますscikit-learnで下記のように実装できます。
[In]
from sklearn.preprocessing import PolynomialFeatures
a = np.array([[1,10,100],[2,20,200],[3,30,300]])
a = pd.DataFrame(a, columns=['x','y','z'])
display(a)
b = PolynomialFeatures(include_bias=False).fit_transform(a)
pd.DataFrame(b, columns=['x','y','z','x^2','xy','xz','y^2','yz','z^2'])
[Out]
左がa(処理前)、右がb(交互作用特徴量で処理)
3.理論:非線形回帰
非線形回帰の用語や理論について紹介します。
3-1.線形回帰の特徴と限界
単回帰(線形回帰)モデルは文字通り次元に対して線で値を推論します($${x_0=1}$$でバイアス項)。
$$
\begin{aligned}
y &= w_{0}+w_{1}x_{1}
\\&=\begin{bmatrix} w_{0}&w_{1}\end{bmatrix} \begin{bmatrix} x_{0} \\ x_{1} \end{bmatrix}
\\&=\bf w^Tx
\end{aligned}
$$
よってモデルの解釈性が高い反面、表現力には乏しいため、データが複雑(曲がりがある、ノイズが大きいなど)だと値をうまく予測できません。
今回のデータは特徴量は1次元のため重回帰は使用できず単回帰ではこれ以上の最適化は不可能となります。
[IN]
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
linear = LinearRegression()
linear.fit(df[['x']], df['y'])
print(f'単回帰の係数 傾きa: {linear.coef_}、切片b: {linear.intercept_:.3f}')
print(f'決定係数:{r2_score(df["y"], linear.predict(df[["x"]])):.3f}')
X = np.linspace(-1.5, 2.5, 100)
y_pred = linear.predict(X.reshape(-1, 1))
sns.scatterplot(x='x', y='y', data=df, label='データ')
sns.lineplot(X, y_pred, color='red', label='予測値')
plt.legend(), plt.grid()
plt.show()[OUT]
単回帰の係数 傾きa: [-0.207]、切片b: 0.357
決定係数:0.163
3-2.モデルの表現力向上:多項式回帰
別のデータを追加せず、表現力を向上させる手法として非線形変換があります。その中でも「特徴量を累乗して新しい特徴量を作成し非線形化」する手法を多項式回帰と呼びます。
3-2-1.Case1:2乗項を追加
具体例として単回帰$${y=w_{1}x_{1} +w_{0}}$$に説明変数$${x_1}$$の2乗の項を追加しました。実装はsklearnの"PolynomialFeatures"で実施しており、バイアス項も追加しました。
2乗項を追加することでカーブを描けるようになり非線形になったため、より良いモデルになりました。なお数式を見ると「2乗項、1乗項、バイアス項の重み付き和」であることが分かります。つまり多項式回帰は各変数の重み付き和であることが分かります。
$$
\begin{aligned}
y &= w_{2}x_{1}^2+w_{1}x_{1} +w_{0}
\\&=\begin{bmatrix} w_{0}&w_{1}&w_{2}\end{bmatrix}
\begin{bmatrix} x_{0} \\ x_{1}\\ x_{1}^2 \end{bmatrix}
\\&=\bf w^Tx
\end{aligned}
$$
[IN]
#2次関数の回帰: y=ax^2+bx+c (重回帰と同じ)
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2, include_bias=True)
x_poly_2dim = poly.fit_transform(df[['x']])
display(pd.DataFrame(x_poly_2dim).rename(columns={0: '1', 1: 'x', 2: 'x^2'}).head(3))
#2次関数の回帰
linear = LinearRegression()
linear.fit(x_poly_2dim, df['y'])
print(f'係数(2次回帰) a:{linear.coef_}、b:{linear.intercept_:.3f}')
y_pred_linear_2dim = linear.predict(x_poly_2dim)
sns.scatterplot(x='x', y='y', data=df, label='データ')
sns.lineplot(x=df['x'], y=y_pred_linear_2dim, color='red', label='2次関数回帰')
plt.show()[OUT]
係数(2次回帰) a:[ 0. -0.226 0.017]、b:0.348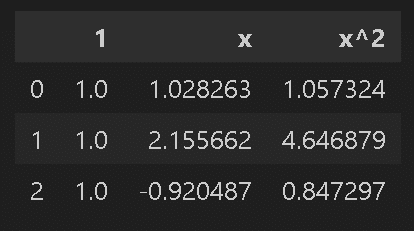

3-2-2.Case2:3乗項まで追加
次に単回帰$${y=w_{1}x_{1} +w_{0}}$$に説明変数$${x_1}$$の2乗項、3乗項を追加しました。実装はsklearnの"PolynomialFeatures"で実施しており、バイアス項も追加しました。
3乗項を追加することでモデルの表現力が格段に上がり、想定に近いカーブとなりました。多項式回帰の累乗項を増やすと表現力が向上するが、その分だけ過学習しやすいことが判断できます。
$$
\begin{aligned}
y &= w_{3}x_{1}^3+w_{2}x_{1}^2+w_{1}x_{1} +w_{0}
\\&=\begin{bmatrix} w_{0}&w_{1}&w_{2}&w_{3}\end{bmatrix}
\begin{bmatrix} x_{0} \\ x_{1}\\ x_{1}^2\\ x_{1}^3 \end{bmatrix}
\\&=\bf w^Tx
\end{aligned}
$$
[IN]
#3次関数の回帰: y=ax^3+bx^2+cx+d
poly = PolynomialFeatures(degree=3, include_bias=True)
x_poly_3dim = poly.fit_transform(df[['x']])
display(pd.DataFrame(x_poly_3dim).rename(columns={0: '1', 1: 'x', 2: 'x^2', 3: 'x^3'}).head(3))
#モデルの作成
linear = LinearRegression()
linear.fit(x_poly_3dim, df['y'])
print(f'係数(3次回帰) a:{linear.coef_}、b:{linear.intercept_:.3f}')
y_pred_linear_3dim = linear.predict(x_poly_3dim)
sns.scatterplot(x='x', y='y', data=df, label='データ')
sns.lineplot(x=df['x'], y=y_pred_linear_3dim, color='red', label='3次関数回帰')
plt.show()[OUT]
係数(3次回帰) a:[ 0. -0.477 -0.445 0.28 ]、b:0.579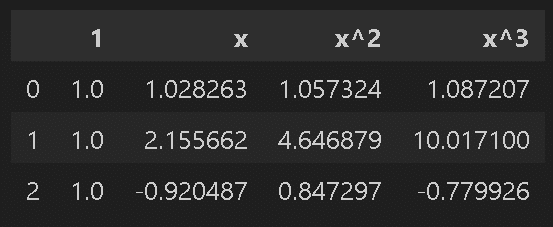

4.基底関数
4-1.基底関数/特徴ベクトルとは
基底関数$${\phi_i(x)}$$(basis function)とは、任意の関数を複数組み合わせて表現する際の基となる関数であり、データをより表現力豊かな空間に変換するために使用されます。難しく言うと「基底関数$${\phi_i(x)}$$によって入力データ$${x}$$を写像し、より高次元な空間に変換」します。
既定関数によって並べたベクトル$${\mathbf{\phi(x)}=(\phi_0(x), \phi_1(x), \cdots, \phi_H(x))^T}$$を$${x}$$の特徴ベクトル(feature vector)と呼びます。
多項式回帰やガウス過程回帰では基底関数を用いて説明変数を非線形に変換し、より複雑なデータの特徴を捉えることができます。
4-2.多項式回帰の基底関数
例として多項式回帰で説明します。前節で非線形なデータに対応するため1次元の説明変数$${x_{1}}$$の累乗項を使用しました。これはつまり説明変数$${x_{1}}$$を関数$${\phi(x)}$$で累乗に変換したと考えられます。つまり基底関数は$${\phi_i(x) = x^i (i = 0, 1, 2, ...)}$$として表現できます。
0乗(バイアス項)を$${\phi_0(x)}$$、恒等変換を$${\phi_1(x)}$$, 2乗式を$${\phi_2(x)}$$, 3乗式を$${\phi_3(x)}$$とすると下記の通り記載できます。
(後述での説明のため$${\bf w}$$と$${\bf X}$$の行列を入れ替えました)
$$
\begin{aligned}
y &= w_{3}x_{1}^3+w_{2}x_{1}^2+w_{1}x_{1} +w_{0}
\\&=\begin{bmatrix} x_{0}&x_{1}&x_{1}^2&w_{1}^3\end{bmatrix}
\begin{bmatrix} w_{0} \\ w_{1}\\ w_{2}\\ w_{3}\end{bmatrix}
\\&=\begin{bmatrix} \phi_{0}(x_{1})& \phi_{1}(x_{1}) & \phi_{2}(x_{1}) & \phi_{3}(x_{1})\end{bmatrix}
\begin{bmatrix} w_{0} \\ w_{1}\\ w_{2}\\ w_{3}\end{bmatrix}
\\&=\bf \phi(x)^Tx
\end{aligned}
$$
説明変数を別の変数に変換する元となる関数を基底関数と呼びます。
4-3.その他の基底関数(三角関数)
多項式回帰では基底関数として$${Φ_i(x) = x^i (i = 0, 1, 2, ...)}$$を使用しましたが、基底関数は多種の関数を選定できます。三角関数(sin(x) や cos(x) など)を基底関数として使用することもでき、例えば周期的なデータに適用することができます。この回帰モデルを三角関数回帰と呼びます。
前節と同様に三角関数を基底関数として表現力を向上させました。
【Case.A:$${\sin(x)}$$を追加】
基底関数$${\phi(x)}$$に三角関数$${\sin(x)}$$を使用しました。$${\sin(x)}$$の影響で曲線+周期性が出来ましたが、十分な表現力とは言えませんでした。
$$
\begin{aligned}
y &= w_{1}\sin(x_{1}) + w_{0} \\&=\begin{bmatrix} 1 & \sin(x_{1})\end{bmatrix} \begin{bmatrix} w_{0} \\ w_{1}\end{bmatrix}
\\&=\begin{bmatrix} \phi_{0}(x_{1})& \phi_{1}(x_{1})\end{bmatrix} \begin{bmatrix} w_{0} \\ w_{1}\end{bmatrix}
\\&=\bf \phi(x)^Tx
\end{aligned}
$$
[IN]
#xにsin(x)を追加
df_add_basicfunc = df.copy()
df_add_basicfunc['sin(x)'] = np.sin(df['x'])
X = df_add_basicfunc.drop(columns=['y'])
y = df_add_basicfunc['y']
display(X.head())
#モデルの作成
linear = LinearRegression()
linear.fit(X, y)
print(f'係数(基本関数追加) a:{linear.coef_}、b:{linear.intercept_:.3f}')
y_pred_linear_add_basicfunc = linear.predict(X)
sns.scatterplot(x='x', y='y', data=df, label='データ')
sns.lineplot(x=df['x'], y=y_pred_linear_add_basicfunc, color='red', label='基本関数追加')
plt.show()[OUT]
係数(基本関数追加) a:[ 0.106 -0.5 ]、b:0.353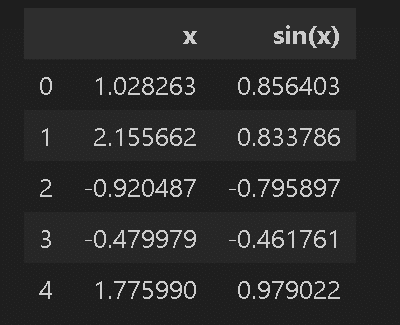

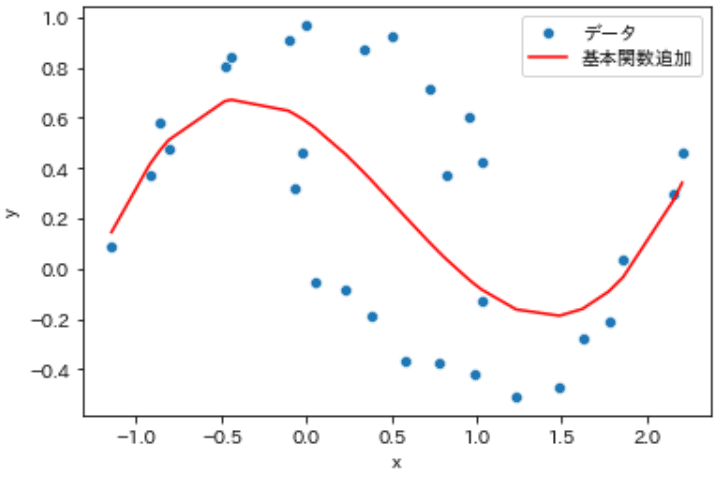
【Case.B:$${\sin(x)}$$と$${\cos(x)}$$を追加】
先ほどの結果では不十分だったので基底関数$${\phi(x)}$$に三角関数$${\sin(x)}$$と$${\cos(x)}$$を使用しました。表現力が格段に上がっておりよいフィットが得られました。
$$
\begin{aligned}y &= w_{2}\cos(x_{1})+ w_{1}\sin(x_{1}) + w_{0}
\\&=\begin{bmatrix} 1 &\sin(x_{1}) & \cos(x_{1})\end{bmatrix} \begin{bmatrix} w_{0} \\ w_{1}\\ w_{2}\\ \end{bmatrix}
\\&=\begin{bmatrix} \phi_{0}(x_{1})& \phi_{1}(x_{1}) & \phi_{2}(x_{1})\end{bmatrix} \begin{bmatrix} w_{0} \\ w_{1}\\ w_{2}\\ \end{bmatrix}
\\&=\bf \phi(x)^Tx
\end{aligned}
$$
[IN]
#xにsin(x)とcos(x)を追加
df_add_basicfunc = df.copy()
df_add_basicfunc['sin(x)'] = np.sin(df['x'])
df_add_basicfunc['cos(x)'] = np.cos(df['x'])
X = df_add_basicfunc.drop(columns=['y'])
y = df_add_basicfunc['y']
display(X.head())
#モデルの作成
linear = LinearRegression()
linear.fit(X, y)
print(f'係数(基本関数追加) a:{linear.coef_}、b:{linear.intercept_:.3f}')
y_pred_linear_add_basicfunc = linear.predict(X)
sns.scatterplot(x='x', y='y', data=df, label='データ')
sns.lineplot(x=df['x'], y=y_pred_linear_add_basicfunc, color='red', label='基本関数追加')
plt.show()[OUT]
係数(基本関数追加) a:[ 1.216 -1.682 0.987]、b:-0.403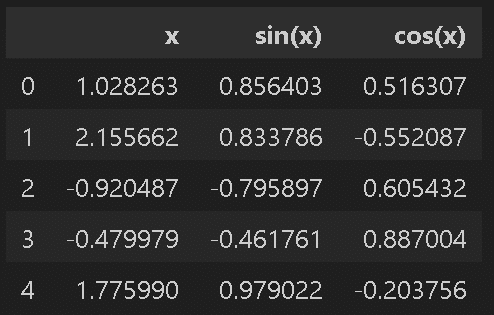
4-4.動径基底関数(RBF)
基底関数の中でも重要な関数として動径基底関数(Radial Basis Function)があります。動径基底関数は、基底関数の中心(原点)からの距離に依存する関数(x が中心 に近いほど値が大きくなり遠くなるほど値が小さくなる特徴)で一般的には下記のガウス関数※が用いられます。
$$
\phi(x) = \exp\left(-\frac{(x-c)^2}{2\sigma^2}\right)=\exp\left(-\frac{||(x-c)||^2}{2\sigma^2}\right)
$$
スケール(length scale)$${\sigma}$$:関数の広がりを調整
関数の中心$${c}$$:ガウス関数の中心の座標
$${||・||}$$:ユークリッド距離(ベクトル(多次元)における距離)
※本により基底関数の分母が$${2\sigma^2}$$と$${\sigma^2}$$があります。理屈上はどちらでも使用可能だがsklearnに合わせて$${2\sigma^2}$を使用
動径基底関数を基底関数として使用する回帰手法である動径基底関数回帰(Radial Basis Function Regression, RBF回帰)はデータの局所的な特徴を捉える能力が高く、様々な非線形データに対応できる手法です。
【※特徴・注意点】
関数の形状がガウス分布と同じであればよい(ガウス分布と数式は異なる)
形状が重要であり絶対値はは重要でない
基底関数に正規化項$${\frac{1}{\sqrt{2\pi\sigma^2}}}$$は不要
データの中心がピークが強く、中心から離れると急激に値が小さくなる
つまり近いデータ同士のピークは強く、遠いデータのピークは小さい
上記より距離をベースにした「類似度」に近い意味を持つ
幅が狭いためデータの局所的な特徴を捉えることができ、基底関数をたくさん用意すれば複雑な非線形データにも対応可能
【参考:データを中心としたピークとは?】
データを7個だけ抽出したうえで、各データに対して基底関数を加えました。見やすいように①データと基底関数の中心を結ぶ直線(グレー)記載、②値が負のデータの基底関数は負に変更、③基底関数の番号記載しました。
結果より、データを中心して分布が広がっていることが確認できます。これに重みをかけて合成すれば複雑な関数も作成可能です。
[IN]
def basic_func(x, center, scale_length):
return np.exp(-(x - center)**2 / (2 * scale_length**2)) #ガウス関数
np.random.seed(54)
df_small = df.copy() #データのコピー
_idx = np.random.choice(df_small.index.values, 7, replace=False) #ランダムに10個のインデックスを取得
df_small = df_small.loc[_idx] #インデックスを指定してデータを抽出
X = np.linspace(-1.5, 2.5, 100)
centers = df_small['x'].values #ガウス関数の中心
scale_length = np.ones(len(centers)) * 0.1 #標準偏差(スケールパラメータ)
y_mappped = basic_func(X.reshape(-1, 1), centers, scale_length) #ガウス関数の出力
fig, ax = plt.subplots(figsize=(8, 5), facecolor='white')
sns.scatterplot(x='x', y='y', data=df_small, label='データ')
for idx in range(len(centers)):
if df_small['y'].iloc[idx]>=0:
ax.plot(X, y_mappped[:, idx], label=r'$\phi_{}(x)$'.format(idx + 1))
ax.text(centers[idx], 0.5+idx*0.1, r'$\phi_{}(x)$'.format(idx + 1), fontsize=12)
else:
ax.plot(X, -y_mappped[:, idx], label=r'$\phi_{}(x)$'.format(idx + 1))
ax.text(centers[idx], -0.5-idx*0.05, r'$\phi_{}(x)$'.format(idx + 1), fontsize=12)
ax.vlines(centers[idx], -1, 1, color='gray', linestyle='dashed', linewidth=0.5)
ax.grid(), ax.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=12)
ax.set(xlabel='x', ylabel='y')
plt.show()
[OUT]
4-5.基底関数の重み付き和(合成関数)
前述の通り説明変数$${x}$$を基底関数$${\phi(x)}$$で変換して重みを掛け合わせることで非線形な関数を作成できました。この形は重回帰と同じであることが確認できます。つまり下記の通りです。
重回帰:各次元の説明変数$${x}$$に重み$${w}$$をかけて合計することで、目的変数$${y}$$に対する特徴量(説明変数$${x}$$)を抽出している。つまり説明変数$${x}$$の重み付き和である。
基底関数の重み付き和:説明変数$${x}$$から生成された基底関数$${\phi(x)}$$に重み$${w}$$をかけて合計することで、目的変数$${y}$$に対する特徴量(基底関数$${\phi(x)}$$)を抽出している。つまり基底関数$${\phi(x)}$$の重み付き和による関数の合成である。
$$
\begin{aligned}
\bf y &=\bf \phi \bf w \\
&=\begin{bmatrix}\phi_{0}(x) & \phi_{1}(x) & \phi_{2}(x) & \cdots & \phi_{D}(x) \end{bmatrix}
\begin{bmatrix}w_{0} \\w_{1} \\w_{2} \\\vdots \\w_{D}\end{bmatrix}
\\&=w_{0}\phi_{0}(x)+ w_{1}\phi_{1}(x) + w_{2}\phi_{2}(x)+ \cdots+ w_{D}\phi_{D}(x)
\\&=\sum_{i=0}^{D}w_i\exp\left(-\frac{(x-c_i)^2}{2\sigma^2}\right)
\end{aligned}
$$
関数の重み付き和による合成関数の作成に関して簡単に可視化してみます。まずは可視化用の関数を作成しました。設計思想は下記の通りです。
基本的な引数は複数の関数をListで渡してプロットする。凡例用にラベルも合わせて渡す。
パラメータとして重みベクトル(weghts)を渡せるようにしておく
weights引数無しなら関数のみ出力
weights引数ありなら、左に関数のみ、右に関数の重み付き和のプロット
テキストで使用した関数と重みを表示
細かい設定追加
x軸・y軸を描写(ax.vlines(), ax.hlines())
画像を保存できるようにsavename引数追加
y軸のサイズは自動調整
[IN]
from scipy.stats import norm
def plotline_multifunc(funcs: List, labels: List[str], weights:List[float]=None, savename:str=None, minyaxis:float=-3.0, maxyaxis:float=3.0):
text = None
# x軸・y軸の描写関数
def plot_vhlines(ax):
ax.vlines(0, -3.0, 3.0, color='black', linewidth=1.5) # x軸
ax.hlines(0, -3.0, 3.0, color='black', linewidth=1.5) # y軸
X = np.linspace(-3.0, 3.0, 100)
if weights:
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6), facecolor='white')
else:
fig, ax1 = plt.subplots(1, 1, figsize=(6, 6), facecolor='white')
#全関数の描写
for func, label in zip(funcs, labels):
y = func(X) # 推論
ax1.plot(X, y, label=label, lw=1.0)
plot_vhlines(ax1) #x軸・y軸の描写
ax1.set(xlabel='x', ylabel='y', xlim=(-3.0, 3.0), ylim=(minyaxis, maxyaxis))
ax1.legend(), ax1.grid()
#合成関数の描写
if weights:
y_compound = np.zeros_like(X)
for func, weight, label in zip(funcs, weights, labels):
y_compound += func(X) * weight
if text is None:
text = f'f(x)={weight:.1f}{label}'
else:
text += f'+{weight}{label}'
ax2.plot(X, y_compound, label='Compound', lw=1.0)
plot_vhlines(ax2) #x軸・y軸の描写
ax2.text(-2.9, maxyaxis*0.75, text, fontsize=12)
ax2.set(xlabel='x', ylabel='y', xlim=(-3.0, 3.0), ylim=(minyaxis, maxyaxis))
ax2.legend(), ax2.grid()
if savename:
if text:
plt.suptitle(f'各関数および関数の重み和')
plt.savefig(f'output/{savename}.png')
plt.show()
#関数の定義
def func_bias(x): return np.ones_like(x) #return 1だとエラー(そのまま1が出力されるため)
def func_x(x): return x # y=x(単回帰:バイアス無し)
def func_x2(x): return x**2# y=x^2
def func_x3(x): return x**3 # y=x^3
def sin(x): return np.sin(x) # y=sin(x)
def cos(x): return np.cos(x) # y=cos(x)
def norm_dist(x): return norm.pdf(x, loc=0, scale=1) # y=標準正規分布(x)基底関数を定義してプロット用関数に渡します。なお重みは関数が合成されていることが分かればいいため数値は適当です。
【多項式】
[IN]
#y=ax+b
funcs = [func_bias, func_x]
labels = ['Bias=1', r'$x$']
# plotline_multifunc(funcs=funcs, labels=labels, savename='case1') #関数表示のみ(合成関数なし)
weights = [1.0, 2.0]
plotline_multifunc(funcs=funcs, labels=labels, weights=weights, savename='case1バイアスあり')
#y=ax^2+bx+c
funcs = [func_bias, func_x, func_x2]
labels = ['Bias=1', r'$x$', r'$x^2$']
# plotline_multifunc(funcs=funcs, labels=labels, savename='case2') #関数表示のみ(合成関数なし)
weights = [0.5, 1.2, 0.3]
plotline_multifunc(funcs=funcs, labels=labels, weights=weights, savename='case2バイアスあり')
#y=ax^3+bx^2+cx+d
funcs = [func_bias, func_x, func_x2, func_x3]
labels = ['Bias=1', r'$x$', r'$x^2$', r'$x^3$']
# plotline_multifunc(funcs=funcs, labels=labels, savename='case3') #関数表示のみ(合成関数なし)
weights = [0.5, 1.2, 0.3, 0.1]
plotline_multifunc(funcs=funcs, labels=labels, weights=weights, savename='case3バイアスあり')
[OUT]


【三角関数】
[IN]
#x+sin(x)
funcs = [func_x, sin]
labels = [r'$x$', r'$sin(x)$']
# plotline_multifunc(funcs=funcs, labels=labels, savename='case4') #関数表示のみ(合成関数なし)
weights = [1.5, 1.0]
plotline_multifunc(funcs=funcs, labels=labels, weights=weights, savename='case4バイアスあり')
#x+sin(x)+cos(x)
funcs = [func_x, sin, cos]
labels = [r'$x$', r'$sin(x)$', r'$cos(x)$']
# plotline_multifunc(funcs=funcs, labels=labels, savename='case5') #関数表示のみ(合成関数なし)
weights = [1.5, 1.0, 0.5]
plotline_multifunc(funcs=funcs, labels=labels, weights=weights, savename='case5バイアスあり')
[OUT]

【動径基底関数(Radial Basis Function)】
[IN]
#複数の正規分布を合成
def norm_dist1(x): return norm.pdf(x, loc=0, scale=1)
def norm_dist2(x): return norm.pdf(x, loc=1.5, scale=1.0)
def norm_dist3(x): return norm.pdf(x, loc=-1.5, scale=1.0)
def norm_dist4(x): return norm.pdf(x, loc=3.0, scale=1.0)
def norm_dist5(x): return norm.pdf(x, loc=-3.0, scale=1.0)
funcs = [norm_dist1, norm_dist2, norm_dist3, norm_dist4, norm_dist5]
labels = [r'$N(x|0,1)$', r'$N(x|1.5,1)$', r'$N(x|-1.5,1)$', r'$N(x|3.0,1)$', r'$N(x|-3.0,1)$']
# plotline_multifunc(funcs=funcs, labels=labels, savename='case6', minyaxis=-1.0, maxyaxis=1.0)
weights = [0.5, -1.0, 0.5, 0.3, 0.1]
plotline_multifunc(funcs=funcs, labels=labels, weights=weights, savename='case6バイアスあり', minyaxis=-1.0, maxyaxis=1.0)
[OUT]
5.動径基底関数回帰
前章で「重みをかけた基底関数を足し合わせることで非線形なモデル」を作成できることを確認しました。基底関数(Basic Function)を複数用意して重み付き和として任意の関数を合成する手法を動径基底関数回帰(radial basis function regression)と言います。
本章では動径基底関数回帰の重みを解析的に計算することでデータにフィッティングさせたモデルを計算できることを確認します。
【注意点:動径基底関数回帰の問題艇】
なお本手法は計算的には正しいですが、基底関数を$${データ数^{次元数}}$$用意する必要があり、同数の重み$${w}$$も必要になります。よって、次元数が増えるとパラメータ$${w}$$が膨大に増え次元の呪いによる性能低下やメモリ量増加などの問題がでます。
ガウス過程回帰などではこの問題に対応するために「データの個数を減らす」や「$${N×N}$$行列$${K_{n,n}}$$を低ランク行列$${Q}$$の積$${K\simQQ^T}$$で近似する」などがあります。
出典:「ガウス過程回帰の基礎から応用」特集号 ガウス過程回帰の基礎
5-1.用語説明:特徴量ベクトル、計画行列
重回帰$${\bf y = \bf X \bf w}$$における$${\bf X }$$を計画行列と呼びます。説明変数$${x_i}$$だけでなく、基底関数$${\phi}$$で変換された行列も計画行列と呼びます。
$$
\begin{aligned}
\underbrace{\begin{bmatrix} y_1 \\ y_2 \\ y_3\\ \vdots \\ y_n \end{bmatrix}}_{\mathbf{\bf y}}
=\underbrace{\begin{bmatrix}x_{10} & x_{11} & x_{12} & \cdots & x_{1D} \\
x_{20} & x_{21} & x_{22} & \cdots & x_{2D} \\
x_{30} & x_{31} & x_{32} & \cdots & x_{3D} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{N0} & x_{N1} & x_{N2} & \cdots & x_{ND}\end{bmatrix}}_{\mathbf{\bf X}}
\underbrace{\begin{bmatrix}w_{0} \\w_{1} \\w_{2} \\\vdots \\w_{D}\end{bmatrix}}_{\mathbf{\bf w}}
\end{aligned}
$$
また基底関数により高次元な空間に変換されたデータ(つまり新しく作成されたベクトル):$${\phi(x)=\begin{bmatrix}\phi_{i0} & \phi_{i1} & \phi_{i2} & \cdots & \phi_{iD}\end{bmatrix}}$$を特徴量ベクトルと呼びます。
$$
\begin{aligned}
\bf y=\bf \Phi \bf w &=
\underbrace{\begin{bmatrix}\phi_{10} & \phi_{11} & \phi_{12} & \cdots & \phi_{1D} \\\phi_{20} & \phi_{21} & \phi_{22} & \cdots & \phi_{2D} \\\phi_{30} & \phi_{31} & \phi_{32} & \cdots & \phi_{3D} \\\vdots & \vdots & \vdots & \ddots & \vdots \\\phi_{N0} & \phi_{N1} & \phi_{N2} & \cdots & \phi_{ND}\end{bmatrix}}_{\mathbf{\bf \Phi}}
\underbrace{\begin{bmatrix}w_{0} \\w_{1} \\w_{2} \\\vdots \\w_{D}\end{bmatrix}}_{\mathbf{\bf w}}
\end{aligned}
$$
5-2.動径基底関数回帰(線形モデル)の解
説明変数$${x}$$に基底関数$${\phi}$$を適用した線形回帰モデルは$${\bf \hat y=\Phi w}$$となります。
$$
\underbrace{\begin{bmatrix}y_{0} \\y_{1} \\y_{2} \\\vdots \\y_{D}\end{bmatrix}}_{\mathbf{\bf y}}
=
\underbrace{\begin{bmatrix}\phi_{10} & \phi_{11} & \phi_{12} & \cdots & \phi_{1D} \\\phi_{20} & \phi_{21} & \phi_{22} & \cdots & \phi_{2D} \\\phi_{30} & \phi_{31} & \phi_{32} & \cdots & \phi_{3D} \\\vdots & \vdots & \vdots & \ddots & \vdots \\\phi_{N0} & \phi_{N1} & \phi_{N2} & \cdots & \phi_{ND}\end{bmatrix}}_{\mathbf{\bf \Phi}}
\underbrace{\begin{bmatrix}w_{0} \\w_{1} \\w_{2} \\\vdots \\w_{D}\end{bmatrix}}_{\mathbf{\bf w}}
$$
この式は重回帰の$${\bf X}$$と$${\bf \Phi}$$以外同じ形であるため重み$${w}$$の解は下記の通りとなります。
$$
\bf w=(\Phi^T\Phi)^{-1}\Phi^Ty
$$
5-3.Pythonでの実装
簡単な例で基底関数を使用して最適解のモデルを作成しました。
【条件/実装の内容】
データは1次元の$${X}$$であり、データ数は5個
基底関数はガウス型の基底関数(Radial Basis Function: RBF)を使用
各データ点が中心となるRBFを計算していき、最後に重みをかけて足し合わせることで全体の関数を作成します。
基底関数の幅sigmaは手動で調整が必要
理解のために以下を可視化
各データ点における基底関数
各データ点における重みを反映した基底関数
全ての基底関数を合成した(最終的な)関数
表示を切り替えることが出来るようloggingモジュールを使用
【数式】
$$
説明変数X = \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \\ x_{5} \end{bmatrix} = \begin{bmatrix} 30 \\ 60 \\ 90 \\ 120 \\ 150 \end{bmatrix}
$$
$$
目的変数y = \begin{bmatrix} y_{1} \\ y_{2} \\ y_{3} \\ y_{4} \\ y_{5} \end{bmatrix} = \begin{bmatrix} 2.1 \\ 3.4 \\ 4.5 \\ 4.8 \\ 4.1 \end{bmatrix}
$$
$$
基底関数\phi(x) = \exp\left(- \frac{(x - \mu)^2}{2\sigma^2}\right)
$$
$$
特徴ベクトル \Phi = \left[ \phi(x_{1}), \phi(x_{2}), ..., \phi(x_{N})\right]^{T}
$$
$$
解析解の重みw = (\Phi^{T}\Phi)^{-1}\Phi^{T}y
$$
$$
x_iに対する推論値y_{pred,i} = \phi(x_{i})^{T}w
$$
[IN]
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import logging
np.set_printoptions(precision=3, suppress=True)
logging.basicConfig(level=logging.DEBUG)
#データ
X = np.array([30, 60, 90, 120, 150]) #コーヒーの抽出時間
y = np.array([2.1, 3.4, 4.5, 4.8, 4.1]) #コーヒーの味 (Score)
#基底関数の定義
def radial_basis_function(x, mu, sigma):
return np.exp(- (x - mu)**2 / (2 * sigma**2))
# 特徴ベクトルを訓練データXに対して作成
sigma = 20 # 基底関数の幅
feature_vec = np.empty((X.shape[0], X.shape[0]))
logging.info(f'特徴ベクトル形状:{feature_vec.shape}')
for i, mu in enumerate(X):
feature_vec[:, i] = radial_basis_function(X, mu, sigma)
logging.debug(feature_vec[:, i])
# 重みの計算
weights = np.linalg.inv(feature_vec.T @ feature_vec) @ feature_vec.T @ y
logging.info(feature_vec)
logging.info(weights)
# 等間隔の点に対する予測
x = np.linspace(0, 180, 100)
y_pred = np.empty(x.shape[0])
for i, x_i in enumerate(x):
feature_vec_test = radial_basis_function(x_i, X, sigma) #データ点 :x_iにおける各基底関数の値
y_pred[i] = feature_vec_test @ weights #各基底関数の値と重みの内積
# 描画
fig, ax = plt.subplots(1, 1, figsize=(8, 5), facecolor='w')
ax.scatter(X, y, label='data') #データ #基底関数
for i, mu in enumerate(X):
ax.plot(x, radial_basis_function(x, mu, sigma) , color='yellow', label=f'RBF_{i+1}') #重み (weights)含めた基底関数
for i, mu in enumerate(X):
ax.plot(x, radial_basis_function(x, mu, sigma) * weights[i], label=f'w_{i+1}×RBF_{i+1}')
ax.plot(x, y_pred, color='red', label=f'RBF prediction')
ax.set(xlabel='x', ylabel='y', title=f'RBF:σ={sigma}')
ax.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=12)
ax.grid()
plt.show()
[OUT]
INFO:root:特徴ベクトル形状:(5, 5)
DEBUG:root:[1. 0.325 0.011 0. 0. ]
DEBUG:root:[0.325 1. 0.325 0.011 0. ]
DEBUG:root:[0.011 0.325 1. 0.325 0.011]
DEBUG:root:[0. 0.011 0.325 1. 0.325]
DEBUG:root:[0. 0. 0.011 0.325 1. ]
INFO:root:
[[1. 0.325 0.011 0. 0. ]
[0.325 1. 0.325 0.011 0. ]
[0.011 0.325 1. 0.325 0.011]
[0. 0.011 0.325 1. 0.325]
[0. 0. 0.011 0.325 1. ]]
INFO:root:[1.43 1.963 2.898 2.813 3.154]
上記より各データ点で基底関数RBFを作成し、解析的に重み$${w}$$を算出してRBFにかけ合わせて合成することでデータに合わせた非線形なモデルが得られました。
注意点としてRBFはハイパーパラメータを含んでおり、その数値が適切でないと意図しないモデルとなります。下記はσを適当にずらしましたが、本ケースではσが小さすぎると異常な曲線が得られました。



6.補足情報
6-1.多項式回帰・非線形回帰の問題点:次元の呪い
次元の呪い(Curse of dimensionality)とは、空間の次元が増えるのに対応して問題の算法が指数関数的に大きくなるため計算量や必要データ量が過剰に増える現象です。
先ほどの動径基底関数では複数の基底関数(Scaleは同じにして中心位置だけずらしたもの)を用意して重み付き和を計算することで非線形な関数を作成できました。今回はデータ数が分かっているため良いですが、基本的にデータは連続値であり無限まだとりえますが、基底関数を無限個も作成できません(PCが計算できない)。


また多次元になると指数的に次元が増加します。もし基底関数が1次元で10個の場合、2次元=$${10^2=100}$$, 3次元=$${10^3=1,000}$$となります。
理解のため2次元の分布で考えます。動径基底関数は下記を使用しました。
$$
f(x, y) = \exp\left(-\frac{(x-\mu_x)^2}{2\sigma_x^2}\right) \exp\left(-\frac{(y-\mu_y)^2}{2\sigma_y^2}\right)
$$
説明変数が1次元の場合は基底関数の重み付き和で線を作成しましたが、説明変数が2次元の場合は面を作成する必要があります。つまり1次元では線上に基底関数を配列するのに対して、2次元では面に基底関数を配列するため次元数が2乗となります。
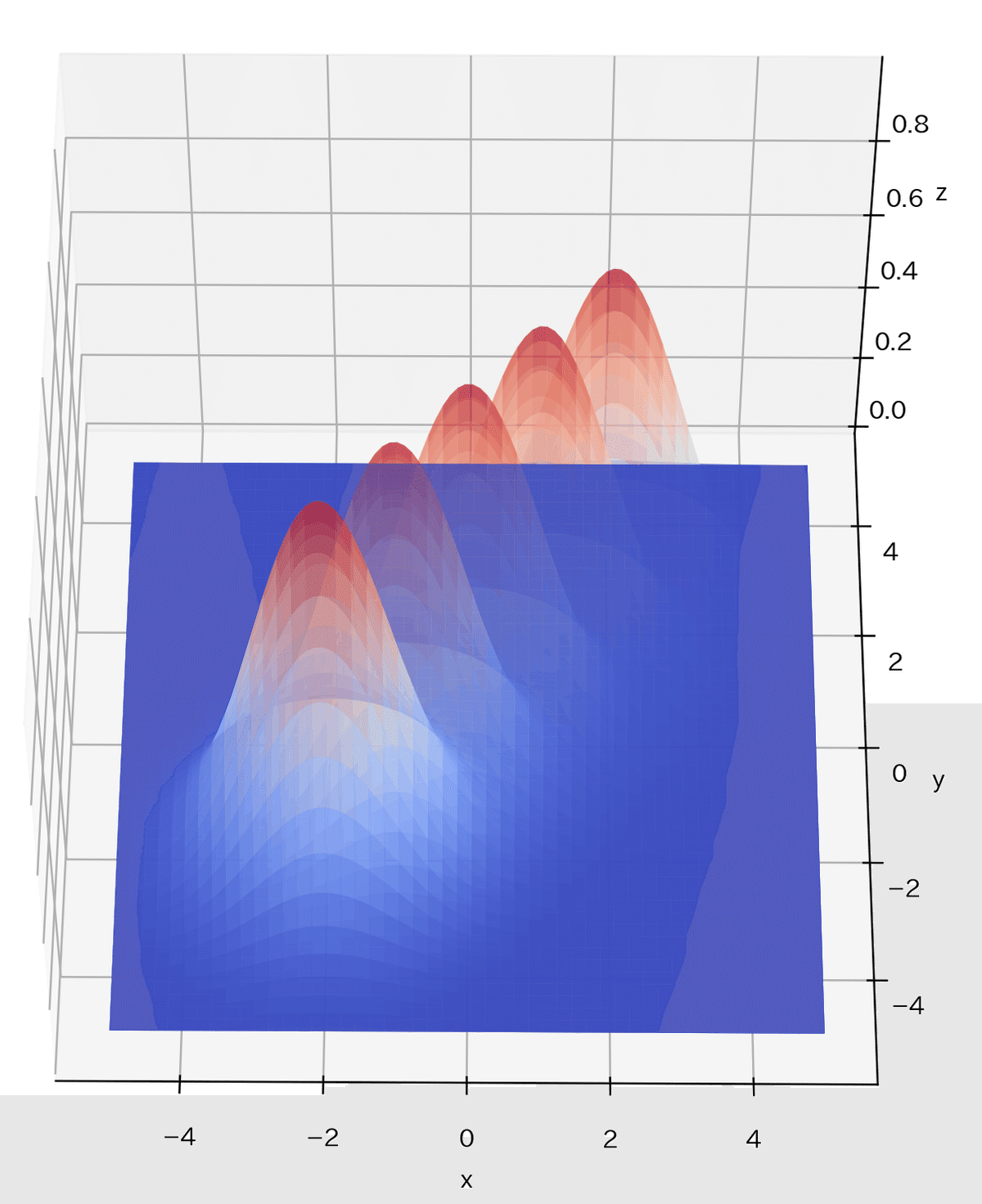
サンプルとして3次元空間に対して基底関数を適当に5つ配置しました。高次元になると空間が広がるため基底関数を次元増加分だけ配置しないと空間が埋まらないことが見て確認できました。
[IN]
%matplotlib qt
#3次元の動径基底関数によるプロット作成
from mpl_toolkits.mplot3d import Axes3D
def basic_func2dim(x, y, mu, s):
return np.exp(-(x-mu[0])**2/(2*s[0]**2)) * np.exp(-(y-mu[1])**2/(2*s[1]**2)) #2次元の動径基底関数
def plot_basic_func2dim(mu, s, ax, label):
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = basic_func2dim(X, Y, mu, s)
ax.plot_surface(X, Y, Z, label=label, cmap='coolwarm', alpha=0.5)
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')
plot_basic_func2dim(mu=[0, 0], s=[1, 1], ax=ax, label='基底関数1')
plot_basic_func2dim(mu=[1, 1], s=[1, 1], ax=ax, label='基底関数2')
plot_basic_func2dim(mu=[-1, -1], s=[1, 1], ax=ax, label='基底関数3')
plot_basic_func2dim(mu=[2, 2], s=[1, 1], ax=ax, label='基底関数4')
plot_basic_func2dim(mu=[-2, -2], s=[1, 1], ax=ax, label='基底関数5')
ax.set_xlabel('x'), ax.set_ylabel('y'), ax.set_zlabel('z')
plt.show()
[OUT]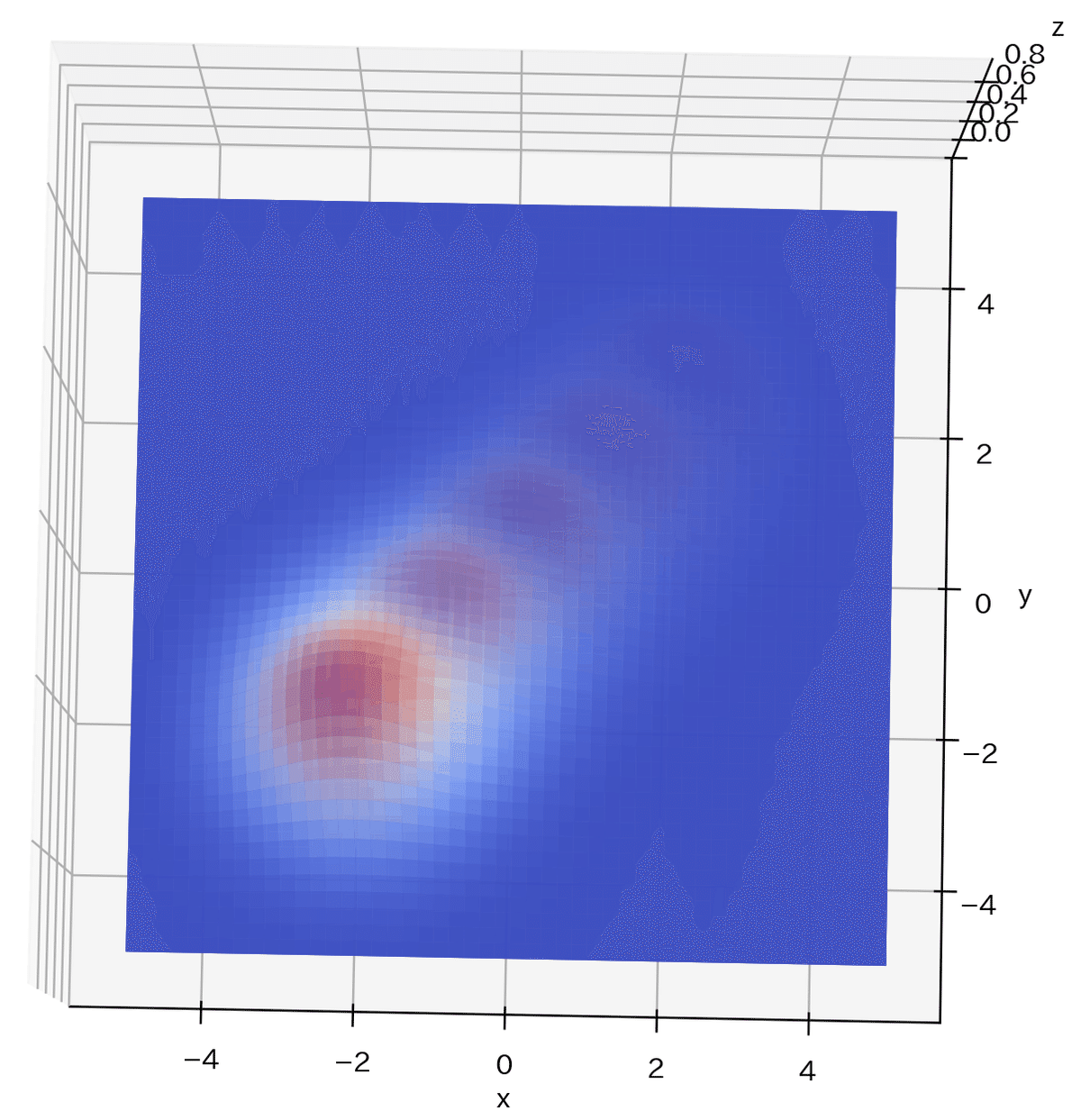


7.実装:多項式回帰
多項式回帰は前述の通りPolynomialFeaturesで交互作用特徴量を作成して、重回帰で計算することで実装できます。
サンプルとしてsklearnのdiabetesデータセット(回帰用)を使用します。
[IN]
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
from mpl_toolkits.mplot3d import Axes3D
from sklearn import datasets
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from tqdm import tqdm
from typing import Tuple, List, Dict, Union, Any, Optional
import os
import glob
diabetes = datasets.load_diabetes()
data = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
target = pd.Series(diabetes.target, name='target')
df = pd.concat([data, target], axis=1)
print(f'df.shape:{df.shape}')
X, y = df.drop(columns=['target']), df['target'][OUT]
df.shape:(442, 11)
まずは通常の重回帰で計算した結果R2スコア=0.518となりました。
[IN]
#線形回帰
linear = LinearRegression()
linear.fit(X, y) #学習
y_pred_linear = linear.predict(X) #予測
print(f'R2 Score:{r2_score(y, y_pred_linear):.3f}')[OUT]
R2 Score:0.518次に交互作用特徴量で次元を作成します。説明変数は10次元であり、下記計算+1(バイアス項)を足すことで新しく66個の次元を作成しました。多項式回帰でのR2スコア=0.592であり性能の改善が確認できました。
$$
\begin{aligned}
Features &=自身の変数の2乗項+他の変数との組み合わせ
\\&= d +\binom{d}{2}
\\&= d + \frac{d(d - 1)}{2}
\\&= 10 + \frac{10(10 - 1)}{2}
\\&= 65
\end{aligned}
$$
[IN]
#多項式回帰
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)
print(f'X_poly.shape:{X_poly.shape}')
linear = LinearRegression()
linear.fit(X_poly, y) #学習
y_pred_linear = linear.predict(X_poly) #予測
print(f'R2 Score:{r2_score(y, y_pred_linear):.3f}')[OUT]
X_poly.shape:(442, 66)
R2 Score:0.592参考資料
あとがき
次はリッジ・ラッソ回帰、ベイズ線形回帰とガウス過程回帰
ー>多分確率分布のサンプリングでMCMCの学習がいる
ー>ここからベイズ最適化までもっていく(多分有料化)
この記事が気に入ったらサポートをしてみませんか?
