
『君の名は。』のラストシーンで瀧と三葉がすれ違う確率<後編>ーー東大出身の理学博士が素朴で難しい問いを物理の言葉で語るエッセイ「ミクロコスモスより」㉑
前編はこちらから
実際の三葉と瀧の出会いは、並走する(すれ違う?)電車の中でした。朝の通勤時間帯にちょうど電車が並走するチャンスというのは限られているため、仮に毎朝同じ電車に乗る生活をしていたとすると、より遭遇確率は上げられるように思われます。
もっともシンプルなケースだと、複々線の路線で待ち合わせる電車同士に乗っていると、駅を同時に発車してしばらく並走するのが確実になります※3。しかし、それではあまりにも自明なので、三葉と瀧のように中央線快速電車と各駅停車の場合に限定して考えましょう。
※3 例えば、小田急線成城学園前駅の各駅停車と急行電車、京王線笹塚駅の京王線と都営新宿線、東武東上線和光市駅の東武線急行電車と東京メトロ線直通電車などが有名です。
こちらの動画のように、中央・総武緩行線の信濃町-千駄ヶ谷駅間では、北側に中央快速線の上下線が並行しており、この区間はあまり高速運転をしない中央快速線と並走することがよくあります。したがって、中央・総武緩行線の中野方面行き電車が信濃町駅を発車した直後に中央快速線が信濃町駅を通過するような前後関係になっていれば、十秒程度にわたって両者がぴったり並走する状況が生まれることになります。
2023年末の時点で、平日朝のラッシュ時に信濃町駅を中野方面に発車する電車の時刻は次の通りです。
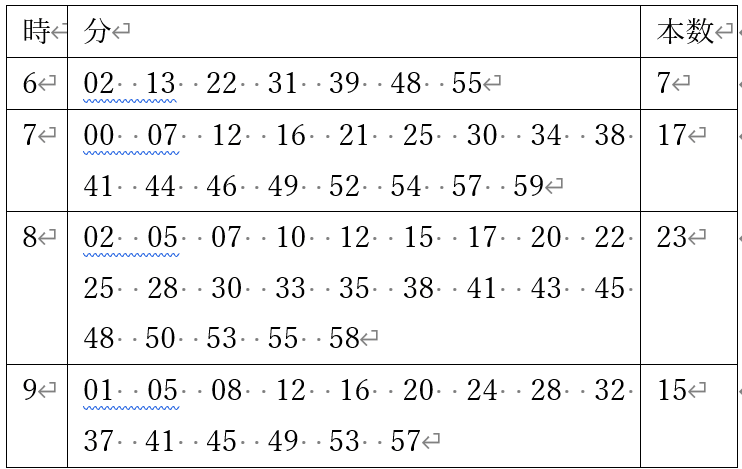
同様に、中央快速線の四ツ谷駅高尾方面の時刻表を抜粋すると次の通りです。

次の動画で計測すると、中央快速線が四ツ谷駅を発車して信濃町駅を通過するまでにかかる時間は1分16秒です。通過時の速度はこの動画を見るだけでは分かりませんが、$${v = 90~{\rm km}/{\rm h}}$$ 程度だと思うことにしましょう。
また、中央・総武線(緩行線)が信濃町駅を発車して最高速度に到達するまでの時間はおよそ$${t = 30}$$秒です。最高速度が同じ$${v}$$だとすると、加速度はおよそ$${a = v / t}$$ということになります※4。発車してから最高速度に到達するまでに移動する距離は$${x_l = \frac{1}{2}at^2}$$で求められます。同じ時間で快速線が進む距離は$${x_r = vt = 2x_l}$$と、緩行線の2倍になるため、緩行線が信濃町駅を発車した15秒後に同駅を通過した快速線があれば、その2本の電車はちょうどタイミングよく並走することになります。
※4 実際には、電車の加速は等加速度的ではないですが、駅間の一部でも並走すればよいと思えば、多少粗い計算でも許されるでしょう。また、電車の運行時刻は実際には5秒や10秒の単位で定められていますがそこまでの具体的な情報は分からないため、公開されている時刻表は全て0秒の発車時刻だと思うことにします。
上記をまとめると、中央快速線が四ツ谷駅を発車したちょうど1分後に信濃町駅を発車する緩行線があれば、並走することになります。そのような組み合わせを取り出すと、次の通りになります。

三葉と瀧がいずれも6時台から9時台の電車を自由に選べると仮定すると、中央・総武緩行線を利用する三葉は62本の選択肢が、中央快速線を利用する瀧は71本の選択肢があります。したがって、二人が乗る電車の選び方は62×71=4402通りあります。その中で、電車が並走する組み合わせは21通りです。したがって、並走する電車に乗れる確率は
$$
\frac{21}{4402} = 0.48\%
$$
になります。
これは、年間で200日電車で通勤すると仮定すると、およそ年に1回の割合で遭遇できることになります。
より現実的に考察してみましょう。
毎日出勤時間は決まっていて、選ぶ電車は特定の時刻の前後15分以内に入る電車に限定されるとすると、「日々の出勤時間」に応じて遭遇確率が変動することになります。二人の出勤時間がちょうど被っている(並走する電車に乗れたら出会えるタイミング)とすると※5、三葉が信濃町駅を何時に出発するかに応じて並走確率を割り出すと、次の通りになります。
※5 よくよく考えると、これがそもそも前提に無ければ、遭遇する可能性は極めて低くなります。9時出勤の人と13時出勤の人は何年経っても出会えないでしょう。

ここから、いくつかのことが分かります。まず、7時15分より前の時間帯では、並走することはできません。その次に確率が低いのは8時20分ごろで、0.59%、すなわち170日に一回、つまりだいたい1年に1回の割合になります。たとえ同じ時間帯の中で選ぶ電車に偏りがあったとしても、前後15分の範囲でランダムに選んでいる限りは、数年以内には出会えることになるでしょう。
したがって、毎朝同じルートを同じタイミングで辿っている限りは、遭遇確率は低くても数年に1度と、さほど奇跡的ではないということが分かります。この場合も①と同様に、
1. まずSNS等を駆使して、相手と同じ時間帯に乗車するようにする。(ただし、相手が下り方向の中央快速線に乗って通勤し、しかも信濃町駅を7:15以降に通過する電車を利用することが前提。)
2. そして、前後15分の電車をランダムに選んで1,2年同じ生活を続ける。
ことによって、あなたは確実に相手と「三葉と瀧」ごっこをすることができます。ぜひ検証結果をこちらまでお寄せください。
プロフィール
小澤直也(おざわ・なおや)
1995年生まれ。博士(理学)。
東京大学理学部物理学科卒業、東京大学大学院理学系研究科物理学専攻博士課程修了。
現在も、とある研究室で研究を続ける。
7歳よりピアノを習い始め、現在も趣味として継続中。主にクラシック(古典派)や現代曲に興味があり、最近は作曲にも取り組む。
