10-1-4 ダミー変数・単回帰係数の性質 ～ 初任給は何に使いましたか？

今回の統計トピック

回帰分析テーマの最終回です。
今回はダミー変数を用いた重回帰モデルと単回帰モデルのMIXです。
政府統計の初任給データを活用して、ダミー変数の偏回帰係数の意味、単回帰分析の結果の読み取りに取り組みます。

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

日本統計学会公式認定　統計検定　2級　公式問題集［CBT対応版］

問題を解く

---

📘公式問題集のカテゴリ

線形モデルの分野　～回帰分析の分野
問4 ダミー変数・単回帰係数の性質（最終学歴別の新卒者初任給額）

試験実施年月
統計検定2級 2019年6月 問17（回答番号31,32）

問題

公式問題集をご参照ください。

利用データ

この記事は、問題集が用いる2018年と直近2022年の【最終学歴別・業種別の「新卒者の初任給額データ」】を利用しています。

• 単位は「万円」です。

• 2018年の金額は「新規学卒者の初任給」です。

• 2022年の金額は「新規学卒者の所定内給与額」です。

• データに含む業種は「鉱業等」「建設業」「製造業」「電気業等」の４業種です。

• 学歴頭のアルファベット、業種頭の数字は並び替え用の記号です。

次の表は2018年「新卒者の初任給額データ」の抜粋（先頭５行）です。

2018年「新卒者の初任給額データ」の先頭５行

初任給を貰った人のイラスト（女性）：「いらすとや」さんより

【出典記載】
「賃金構造基本統計調査（2018年）」（厚生労働省）の「産業別新規学卒者の初任給の推移」
（https://www.e-stat.go.jp/stat-search/files?tclass=000001014754&cycle=0）
「賃金構造基本統計調査（2022年）」（厚生労働省）の「新規学卒者の所定内給与額」
（https://www.e-stat.go.jp/stat-search/files?tclass=000001202291&cycle=0）

【コンテンツ編集・加工の記載】
記事の記載にあたっては、出典記載の資料を加工して作成しています。

解き方

題意
最小二乗法で推定した２つの回帰モデルについて、次の２問を解答します。
① 重回帰モデルの偏回帰係数の意味など
② 単回帰モデルの分析結果の意味など

【条件】
・各モデルに含む誤差項は、各モデルごとに、互いに独立に正規分布$${N(0, \sigma^2)}$$に従います。
・表の$${\hat{\sigma}}$$は$${\sigma^2}$$の不偏推定値の平方根です。
・2018年「新卒者の初任給額データ」の散布図は下の図を参照ください。

公式問題集の記述を改変

2018年「新卒者の初任給額データ」の散布図

クロス集計表（ピボットテーブル）形式にすると次のようになります。
スッキリまとまって見やすいです。

2018年「新卒者の初任給額データ」のクロス集計表

なお、問題には明記されていませんが、回帰モデルの各種推定値の表は「統計ソフトウェアの出力結果」の抜粋です。
この記事では「統計ソフトウェア R の出力結果」の形式で掲載いたします。

① 重回帰モデル

■ 統計ソフトウェア R の出力結果

「新卒者の初任給額データ」の重回帰モデルについて、「統計ソフトウェア R の出力結果」は次のようになりました。

重回帰モデルの出力結果

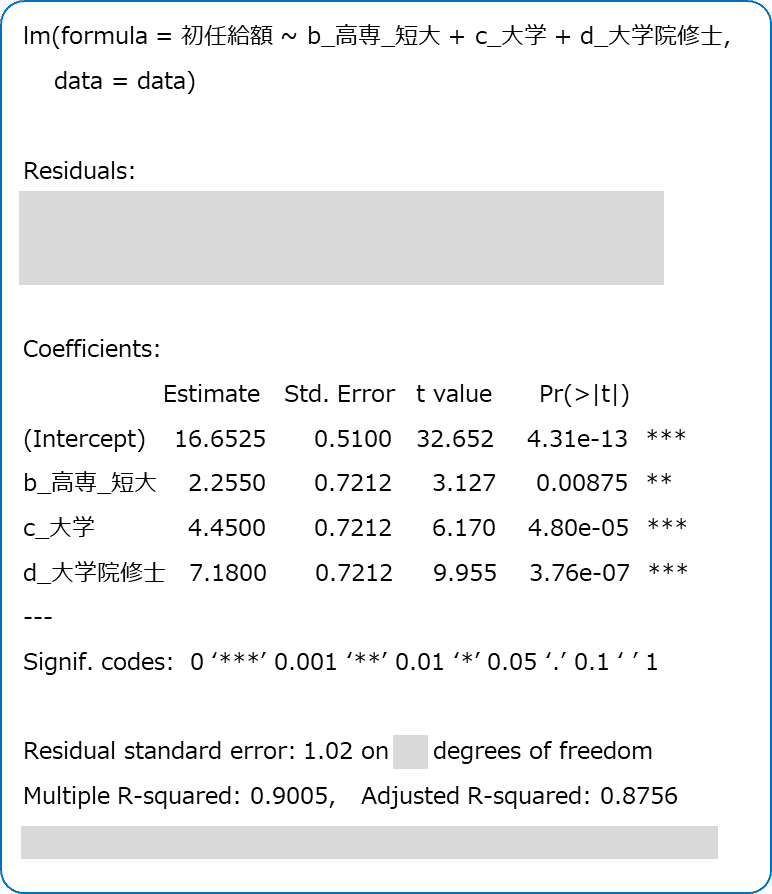
変数名には漢字を用いました。
また、問題では、次の値を四捨五入して小数点第３位に丸めています。
・偏回帰係数の推定値と標準誤差
・決定係数と自由度調整済み決定係数

■ 回帰式

ひとまず、回帰式を書きましょう。

$${初任給額=16.653 + 2.255 \times 高専\_短大 + 4.450 \times 大学 +7.180 \times 大学院修士}$$

■ ダミー変数

変数「学歴」は学歴名称を取り扱う質的変数です。
質的変数の値は数値ではありません。
線形回帰分析の場合、目的変数・説明変数の両方が数値を扱う「量的変数」であることが必要です。
そこで登場するのがダミー変数です。
機械学習界隈で「One-Hot エンコーディング」と呼ばれるものです。

ひとまずダミー変数を見てみましょう。
下表の項目「b_高専_短大」「c_大学」「d_大学院修士」がダミー変数です。
最左の項目「学歴」と比べながら眺めてみましょう。

One-Hot エンコーディング by pandas get_dummies

ダミー変数の値は 0 か 1 のみです。
しかも、ほどんどの値が 0 です。
これはどういうことでしょう・・・？

要約します。
１行目の見出しはダミー変数の項目名です。
１列目の見出しは項目「学歴」の４つの学歴の値です。

$$
\begin{array}{c|c:c:c}
学歴 & \text{b}\_高専\_短大 & \text{c}\_大学 & \text{d}\_大学院修士\\
\hline
\text{a}\_高校 & 0 & 0 & 0 \\
\text{b}\_高専\_短大 & 1 & 0 & 0 \\
\text{c}\_大学 & 0 & 1 & 0 \\
\text{d}\_大学院修士 & 0 & 0 & 1 \\
\end{array}
$$

ダミー変数の値の正体は、該当する学歴のダミー変数に 1 の印を立てていることなのです。

茶柱のイラスト：「いらすとや」さんより

さて、高校にはダミー変数はありません。1 も立っていません。
どのようにして高校を識別するのでしょう？？？
それは「すべてのダミー変数が０の場合は高校」という見方をするのです。

■ ダミー変数と回帰式の考察

学歴別に回帰式にダミー変数の値を当てはめてみましょう。

a 高校
　$${初任給額=16.653 + 2.255 \times 0+ 4.450 \times 0 +7.180 \times 0=16.653}$$
b 高専・短大
　$${初任給額=16.653 + 2.255 \times 1+ 4.450 \times 0 +7.180 \times 0=18.908}$$
c 大学
　$${初任給額=16.653 + 2.255 \times 0+ 4.450 \times 1 +7.180 \times 0=21.103}$$
d 大学院修士
　$${初任給額=16.653 + 2.255 \times 0+ 4.450 \times 0 +7.180 \times 1=23.833}$$

切片$${16.653}$$は高校卒の初任給額の予測値に相当します。
この切片をベース金額とし、学歴の偏回帰係数を足すと、学歴の初任給額の予測値になります。

ダミー変数と回帰式の関係って、案外、シンプルなのです。

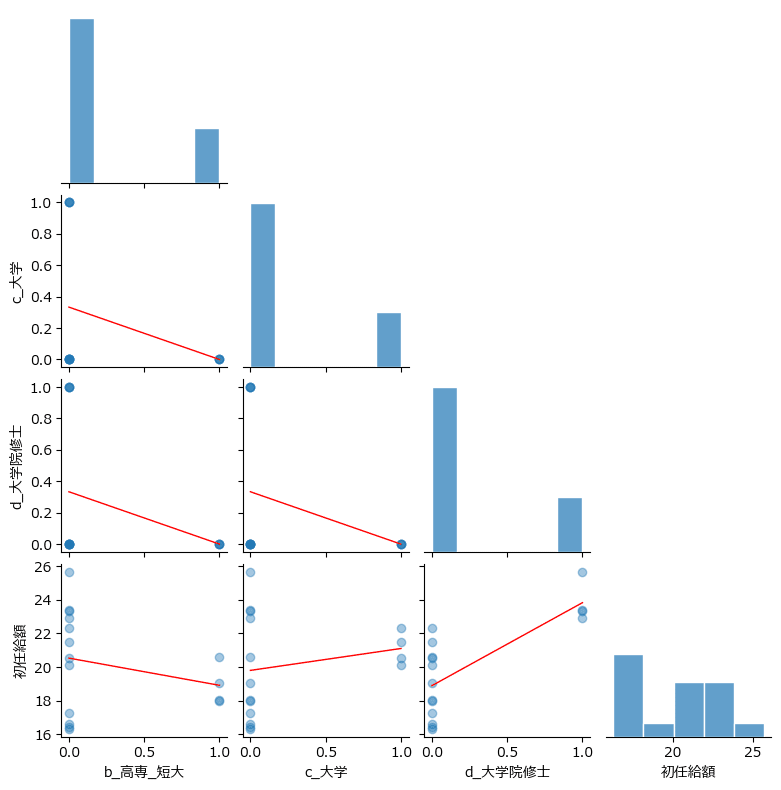
参考に（ならないかもですが）、ダミー変数と目的変数の散布図行列グラフを置いておきます。
最下行に目的変数「初任給額」とダミー変数の１対１のグラフが並んでいます。

目的変数とダミー変数の散布図行列

問題に戻ります。
記述Ⅰ～Ⅲから適当な記述を選びます。

【記述Ⅰ】
推定結果から高校卒の学歴と初任給の関係は分からない。

【考察】
「ダミー変数と回帰式の考察」を振り返りましょう。
切片$${16.653}$$は高校卒の初任給額の予測値に相当します。
つまり、推定結果から高校卒の学歴と初任給の関係は分かります。

記述Ⅰは適切ではありません。

【記述Ⅱ】
大学院修士修了の初任給は大学卒の初任給よりも$${2.73}$$万円高い。

「統計ソフトウェアの出力結果」の関連値を見ておきましょう。

重回帰モデルの出力結果の抜粋

【考察】
「ダミー変数と回帰式の考察」を振り返りましょう。
切片はベース金額となり、学歴に対応する偏回帰係数を加算すると初任給の予測値になります。
大学卒の偏回帰係数は$${4.450}$$万円、大学院修士修了の偏回帰係数は$${7.180}$$万円、これらの差は$${2.73}$$万円です。
つまり、大学院修士修了の初任給は大学卒の初任給よりも$${2.73}$$万円高いのです。

記述Ⅱは適切です。

【記述Ⅲ】
$${P-}$$値は自由度$${13}$$の$${t}$$分布を用いて計算されている。

「統計ソフトウェアの出力結果」の関連値を見ておきましょう。

重回帰モデルの出力結果の抜粋

上表の「Pr(<|t|)」の項目が「$${P-}$$値」です。
隣の「t value」が偏回帰係数の検定に用いられる$${t}$$検定統計量です。
この表の$${P-}$$値は$${t}$$検定統計量の有意確率です。
偏回帰係数の検定における帰無仮説は「その偏回帰係数は０である」です。

【考察】
帰無仮説が正しいとの仮定の下で$${t}$$検定統計量の公式は次のとおりです。

$${t_j = \cfrac{\hat{\beta_j}-0}{\sqrt{\hat{\sigma}^2/ T_{xx_j}}}=\cfrac{\hat{\beta_j}}{\sqrt{\hat{\sigma}^2/ T_{xx_j}}} \sim t(n-p-1)}$$

$${j}$$：観測データの番号、$${\hat{\beta}}$$：回帰係数の推定値、$${\hat{\sigma}^2}$$：残差の不偏分散、$${T_{xx}}$$：説明変数の偏差平方和

$${t}$$検定統計量は自由度$${n-p-1}$$の$${t}$$分布に従います。
このモデルは、標本サイズ$${n=16}$$、説明変数の数$${p=3}$$です、
したがって、自由度は$${16-3-1=12}$$です。
つまり、$${P-}$$値は「自由度$${12}$$」の$${t}$$分布を用いて計算されています。

記述Ⅲは適切ではありません。

重回帰モデルの問題に関する解答をまとめます。
・記述Ⅰは適切でない
・記述Ⅱは適切である
・記述Ⅲは適切でない
まとめると「Ⅱのみ正しい」です。

解答選択肢は ② です。

ダミーヘッドマイクのイラスト：「いらすとや」さんより

② 単回帰モデル

「新卒者の初任給額データ」の重回帰モデルについて、「統計ソフトウェア R の出力結果」は次のようになりました。

単回帰モデルの出力結果

問題では、次の値を四捨五入して小数点第３位に丸めています。
・回帰係数の推定値と標準誤差
・決定係数と自由度調整済み決定係数
また、問題では、残差の標準誤差の切り捨てして小数点第３位に丸めています。

■ 回帰式

ひとまず、回帰式を書きましょう。

$${初任給額=2.323 + 1.187 \times 教育年数x}$$

回帰式をもとにして散布図に回帰直線を描画しましょう。
単回帰モデルは可視化しやすいので、イメージを掴みやすいです！
学歴で固定的な教育年数をあてているので、散らばりません・・・

単回帰モデルの散布図と回帰直線

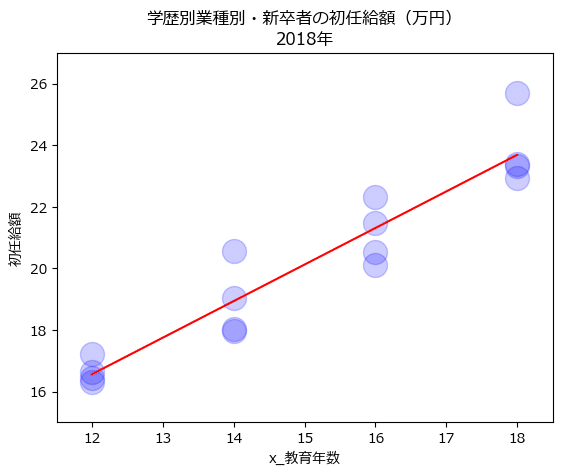
問題に移ります。
記述Ⅰ～Ⅲから適当な記述を選びます。

【記述Ⅰ】
教育年数が１年増えると初任給は$${1.187}$$万円上がる傾向がある。

「統計ソフトウェアの出力結果」の関連値を見ておきましょう。

単回帰モデルの出力結果の抜粋

【考察】
「回帰式」を振り返りましょう。
教育年数$${x}$$の値が１増えると、初任給額の予測値は、傾き$${1.187}$$に１を掛けた$${1.187}$$万円増えます。
つまり、教育年数が１年増えると初任給は$${1.187}$$万円上がる傾向があると言えます。

記述Ⅰは適切です。

【記述Ⅱ】
単回帰モデルでは決定係数と自由度調整済み決定係数は等しい。

「統計ソフトウェアの出力結果」の関連値を見ておきましょう。

単回帰モデルの出力結果の抜粋

決定係数は回帰モデルの当てはめて具合・説明力を示す指標です。
目的変数の全体の変動を示す「総平方和」と、回帰モデルで説明できる変動を示す「回帰による平方和」の比です。
計算式は次のとおりです。

$$
\begin{align*}
R^2&=\cfrac{S_R}{S_T}=1-\cfrac{S_e}{S_T} \\
 \\
決定係数&=\cfrac{回帰による平方和}{総平方和}=1-\cfrac{残差平方和}{総平方和} \\
 \end{align*}
$$

自由度調整済み決定係数は、自由度で平方和を調整することによって、説明変数の数が異なる回帰モデルを比較できる指標です。
計算式は次のとおりです。

$$
\begin{align*}
R^{*2} &= 1 - \cfrac{S_e/(n-p-1)}{S_T/(n-1)} \\
自由度調整済み決定係数&=1- \cfrac{残差平方和/残差の自由度}{総平方和/全体の自由度} \\
\end{align*}
$$

この式の$${n-p-1}$$と$${n-1}$$が自由度です。
$${n-p-1}$$は残差平方和の自由度、$${n-1}$$は総平方和の自由度です。
残差平方和の調整に用いる自由度と総平方和の調整に用いる自由度は異なります。

この単回帰モデルの場合
・残差平方和の自由度は$${14}$$です（$${n-p-1=16-1-1=14}$$）。
・総平方和の自由度は$${15}$$です（$${n-1=16-1=15}$$）。

異なる自由度で調整する「自由度調整済み決定係数」は「決定係数」と異なる値になります。
つまり、単回帰モデルでは決定係数と自由度調整済み決定係数は等しくないです。

記述Ⅱは適切ではありません。

【記述Ⅲ】
切片について、両側検定を行っても片側検定を行っても、$${P-}$$値は同じ$${0.174}$$である。

「統計ソフトウェアの出力結果」の関連値を見ておきましょう。

単回帰モデルの出力結果の抜粋

切片の$${P-}$$値は、回帰係数の検定に用いる$${t}$$値に対応する有意確率です。
この単回帰モデルの自由度は$${n-p-1=16-1-1=14}$$です。
自由度$${14}$$の$${t}$$分布のパーセント点$${1.434}$$に対応する確率を描画してみましょう。

回帰係数のｔ値が従うｔ分布とｐ値

$${t}$$値$${1.434}$$の上側確率は$${8.7\%}$$です。
統計ソフトウェアの出力結果に表示された$${P-}$$値は「両側検定」を想定しており、上側確率$${8.7\%}$$の倍の$${17.4\%}$$なのです。

では「片側検定」の場合はどうなるのでしょう？
実は$${t}$$値$${1.434}$$の上側確率$${8.7\%}$$が片側検定のときの$${P-}$$値なのです。
片側ですから、上のグラフの片方・上側の確率なのです。

つまり、切片について、片側検定の場合の$${P-}$$値は$${0.174}$$の半分の$${0.087}$$です。

記述Ⅲは適切ではありません。

単回帰モデルの問題に関する解答をまとめます。
・記述Ⅰは適切である
・記述Ⅱは適切でない
・記述Ⅲは適切でない
まとめると「Ⅰのみ正しい」です。

解答選択肢は ① です。

日食のイラスト：「いらすとや」さんより

解答

〔1〕②、〔2〕① です。

難易度　ふつう

・知識：ダミー変数、（偏）回帰係数、（偏）回帰係数の検定、決定係数
・計算力：数式組み立て（低）、電卓（低）
・時間目安：2問合計 3分

知る

---

おしながき

公式問題集のデータに接近してみましょう！
今回は2018年と2022年の「新卒者の初任給額データ」を比べてみましょう。
４年間の変化をお楽しみください。

線形回帰モデル

📕公式テキスト：1.6.4 回帰直線（32ページ～）、5.1.5 線形重回帰モデル（171ページ～）など

特集記事のお知らせ

単回帰モデルの詳しい学習ポイントを「特集記事」にまとめました。
ぜひご覧くださいませ。

初任給を2018年→2022年で比較する

2022年データの概要

クロス集計表（ピボットテーブル）形式でデータを見てみましょう。
変化点は、学歴に「専門学校」が追加されたことです。

2022年「新卒者の初任給額データ」のクロス集計表

散布図で２期間を比べてみましょう。
2022年は赤丸、2018年は青丸です。

「新卒者の初任給額データ」の2018年と2022年の散布図

大学卒と大学院修士修了は２～３万円程度増額しているようです。
一方で、高校卒は１万円以下の増額、高専・短大卒は業種間の差が縮まったものの全体として伸びていない感じです。
また、専門学校卒は高専・短大卒よりも業種間の差が大きいです。

それでは重回帰モデルの分析に進みましょう。

重回帰モデル

「統計ソフトウェア R の出力結果」は次のようになりました。

2022年の重回帰モデルの出力結果

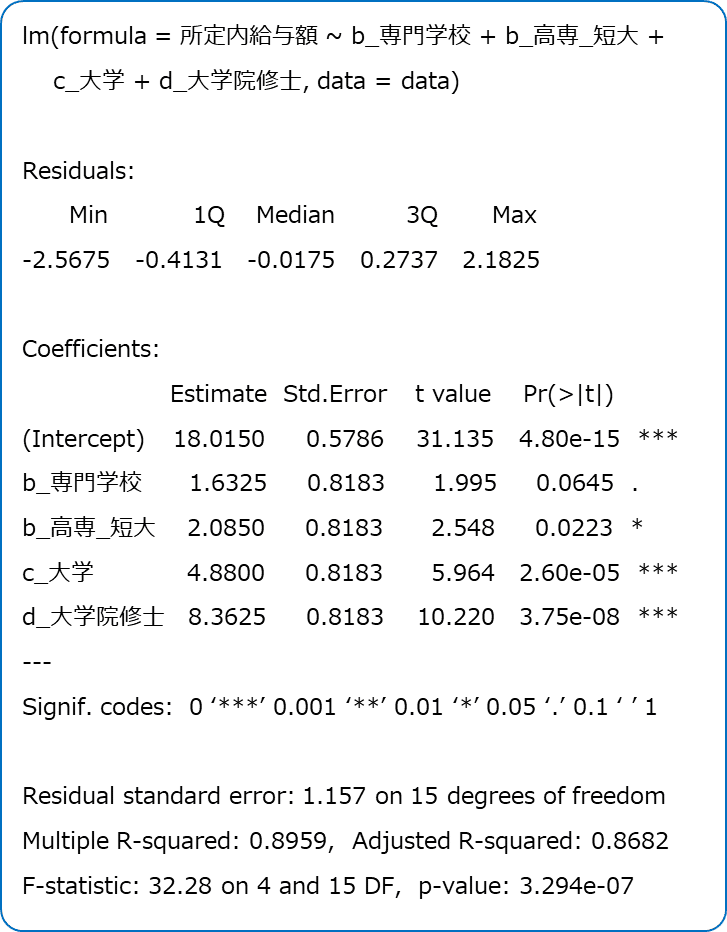
【数値を確認する】

• 自由度調整済み決定係数は$${0.8682}$$です。
  当てはまりの良いモデルと言えるでしょう。

• 回帰の有意性の検定の$${p}$$値は極小です。有意水準$${5\%}$$でこのモデルに含まれる説明変数の中に目的変数の説明に役立つ変数がある、と言えるでしょう。

• 回帰係数の検定の$${p}$$値は、専門学校の回帰係数の推定値が$${5\%}$$を上回っているものの、まあまあ回帰係数は０では無いと言えるでしょう。

【回帰式を使う】
ひとまず学歴別に回帰式にダミー変数の値を当てはめてみましょう。
求めた金額は初任給の予測値に相当します。

a 高校
　$${初任給額=18.0150 + 1.6325 \times 0+ 2.0850 \times 0 +4.8800 \times 0 + 8.3625 \times 0=18.0150}$$
b 専門学校
　$${初任給額=18.0150 + 1.6325 \times 1+ 2.0850 \times 0 +4.8800 \times 0 + 8.3625 \times 0=19.6475}$$
b 高専・短大
　$${初任給額=18.0150 + 1.6325 \times 0+ 2.0850 \times 1 +4.8800 \times 0 + 8.3625 \times 0=20.1000}$$
c 大学
　$${初任給額=18.0150 + 1.6325 \times 0+ 2.0850 \times 0 +4.8800 \times 1 + 8.3625 \times 0=22.8950}$$
d 大学院修士
　$${初任給額=18.0150 + 1.6325 \times 0+ 2.0850 \times 0 +4.8800 \times 0 + 8.3625 \times 1=26.3775}$$

【比較する】
重回帰モデルにもとづき、2018年と2022の初任給の予測値を表にしました。
「増加率/年」は増加率の幾何平均（４乗根）です。
インフレ目標に届いたり届かなかったりしています。

重回帰モデルによる初任給の予測値

可視化してみましょう。
４年間の伸びの様子をイメージできそうです。

【ダミー変数を使ってみて】
「学歴」のような質的変数をダミー変数で「０か１」の数値化して重回帰分析を行うと、回帰式のようなシンプルな「足し算と掛け算」でモデル化できました。

単回帰モデル

「統計ソフトウェア R の出力結果」は次のようになりました。

2022年の単回帰モデルの出力結果

【数値を確認する】

• 自由度調整済み決定係数は$${0.8685}$$です。
  当てはまりの良いモデルと言えるでしょう。

• 回帰の有意性の検定の$${p}$$値は極小です。有意水準$${5\%}$$でこのモデルに含まれる説明変数の中に目的変数の説明に役立つ変数がある、と言えるでしょう。

• 切片の推定値の$${p}$$値は$${0.869}$$と大きな値です。
  有意水準$${5\%}$$で切片が０であるという帰無仮説を棄却できないようです。
  切片の推定値はゼロに近い$${0.3156}$$ですので、切片を０として扱ってもよいのかもしれません。

【回帰式を書く】

ひとまず、回帰式を書きましょう。

$${初任給額=0.3156 + 1.4251 \times 教育年数x}$$

【比較する】
回帰係数を比較してみました。
いまひとつピンときません・・・

単回帰モデルの回帰係数の比較表

可視化してみましょう。
オレンジが2022年、青が2018年です。

単回帰モデルの回帰直線の比較

2022年の回帰直線は2018年を上回っています。
また、2022年の傾きの方が大きいので、教育年数が増えるにつれて、予測値が2018年と2022年との間で差が広がっています。
最終学歴によって初任給の差が広がっているのかもしれません。

以上で回帰分析を終了します。
データは「比較」をすると特徴の輪郭が見えやすくなりますね！
回帰分析も比較が大切だと実感いたしました。

お菓子を選ぶ子供のイラスト（男の子）：「いらすとや」さんより

実践する

---

新卒者の初任給データの回帰分析結果を並べる

新卒者の初任給額データの回帰分析をEXCEL、R、Pythonで実践しましょう！
今回は回帰分析の出力結果をコレクションのように並べてみます。
お好みの曲をBGMにしてお楽しみください♬

コレクター・収集家のイラスト：「いらすとや」さんより

特集記事のお知らせ

EXCEL、R、Pythonの単回帰分析の実践を「特集記事」にまとめました。
ぜひご覧くださいませ。

EXCELで作成してみよう！

データ分析機能の「回帰分析」と回帰直線をプロットした「散布図グラフ」をコレクションしました。

重回帰分析の出力結果

■ 2018年

■ 2022年

単回帰分析の出力結果

■ 2018年

■ 2022年

単回帰モデルの回帰直線の比較

EXCELの分析ツールでサクッと回帰、いかがでしょう。

回帰分析画面で目的変数と説明変数を指定するシーン

💡 ワンポイント

◆ ダミー変数の設定
Ｃ列の「学歴」の値を COUNTIF 関数の条件（"*a_高校*" など）で判別して０または１を設定しています。

◆ 教育年数の設定
ダミー変数の値に次の値を乗じて計算しています。
・専門学校と高専・短大：２年
・大学：４年
・大学院修士：６年

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
サンプルファイルには「新卒者の初任給額データ」が含まれています。

10-1-4_ダミー変数・単回帰係数の性質.xlsx

49.1 KB

ファイルダウンロードについて

ダウンロード

R で作成してみよう！

「統計ソフトウェアの出力結果」、「分散分析」、「散布図行列グラフ」をコレクションしました。

重回帰分析の出力結果

■ 2018年

■ 2022年

単回帰分析の出力結果

■ 2018年

■ 2022年

分散分析（重回帰モデル）の出力結果

■ 2018年

■ 2022年

分散分析（単回帰モデル）の出力結果

■ 2018年

■ 2022年

散布図行列（ psych ライブラリ）

■ 2018年

■ 2022年

Rサンプルファイルのダウンロード
こちらのリンクからRスクリプト形式のサンプルファイル、および、「新卒者の初任給額データ」のCSVファイルをZIP形式でダウンロードできます。

10-1-4_ダミー変数・単回帰係数の性質R.zip

1.91 KB

ファイルダウンロードについて

ダウンロード

■ ZIPファイルの内容（４ファイル）
①10-1-4_ダミー変数・単回帰係数の性質.R
　→2018年データを処理するRスクリプト
②10-1-4_ダミー変数・単回帰係数の性質2022.R
　→2022年データを処理するRスクリプト
③sampledata2.csv
　→2018年データ（ダミー変数化済み）
④sampledata2022_2.csv
　→2022年データ（ダミー変数化済み）

　

Pythonで作成してみよう！

statsmodels を用いて作成した「回帰分析」・「分散分析」と他のライブラリで作成した「各種グラフ」をコレクションしました。

重回帰分析の出力結果

■ 2018年

■ 2022年

単回帰分析の出力結果

■ 2018年

■ 2022年

分散分析（重回帰モデル）の出力結果

■ 2018年

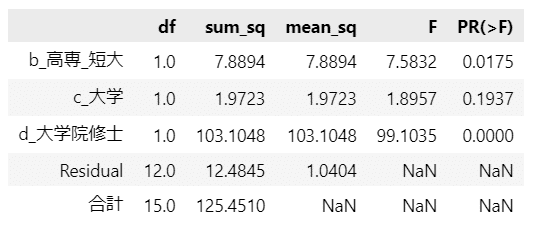
■ 2022年

分散分析（単回帰モデル）の出力結果

■ 2018年

■ 2022年

グラフ

■ 2018年

・散布図（sns.relplot）

・散布図行列（sns.pairplot）

・散布図・回帰直線（pandas.plot.scatter、matplotlib.pyplot.plot）

■ 2018年・2022年

・散布図（pandas.plot.scatter）

・散布図（pandas.plot.scatter）

・散布図・回帰直線（pandas.plot.scatter、matplotlib.pyplot.plot）

💡 ワンポイント

◆ ダミー変数の設定
Pandas の get_dummies を利用しました。

# 学歴をダミー変数化
data = pd.get_dummies(data_orgn, columns=['学歴'], prefix='', prefix_sep='')
data = data.drop('a_高校', axis=1)

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイル、および、「新卒者の初任給額データ」のCSVファイルをZIP形式でダウンロードできます。

10-1-4_ダミー変数・単回帰係数の性質Python.zip

302 KB

ファイルダウンロードについて

ダウンロード

■ ZIPファイルの内容（３ファイル）
①10-1-4_ダミー変数・単回帰係数の性質.ipynb
　→Jupyter Notebook 形式のPythonファイル
②sampledata.csv
　→2018年データ
③sampledata2022.csv
　→2022年データ

---

おわりに

これで４回に渡る回帰分析のテーマを終えます。
回帰分析はとてもメジャーなデータ分析手法なので、EXCEL、R、Pythonなどのツールの充実度が高いです。
ぜひ、お手元のデータで「ひとまず回帰分析」を実行してみましょう。

いろいろなブロガーのイラスト：「いらすとや」さんより

単回帰モデルの特集記事のご紹介

計算式・公式などで押さえる回帰分析の座学と、EXCEL・R・Pythonなどのツールで押さえる回帰分析の実践を２つのブログ記事にまとめました。
ぜひご覧ください！

最後までお読みいただきまして、ありがとうございました。

---

のんびり統計シリーズの記事

次の記事

前の記事

目次