8-9 等分散性の検定 ～ ２標本の母分散の比のＦ検定／Ｆ分布のパーセント点表の下側確率を読む

今回の統計トピック

統計的仮説検定のトピック「２標本の母分散の比の$${F}$$検定」を深掘りします。
$${F}$$分布のパーセント点表から「上側確率」「下側確率」のパーセント点を取得しましょう！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

日本統計学会公式認定　統計検定　2級　公式問題集［CBT対応版］

問題を解いて、知る

---

今回の記事の構成

この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」と「知る」を１つの章にまとめます。
２標本の母分散の比の$${F}$$検定の一連の流れを、手作業で実践いたします。

📘公式問題集のカテゴリ

検定の分野
問9 等分散性の検定（２つの学級の試験の点数）

試験実施年月
統計検定2級 2018年6月 問16（回答番号34）

📕公式テキスト：4.4.3 母分散の比の検定（155ページ～）

問題

公式問題集をご参照ください。

解き方

題意
与えられた条件から２標本の母分散の比の検定で用いる$${F}$$値を求めて、帰無仮説を棄却できるかどうかを判定します。

【条件】
・クラスAの点数は正規分布に従い、標本サイズが21、標準偏差が19.5
・クラスBの点数は正規分布に従い、標本サイズが41、標準偏差が14.5
・標準偏差は不偏分散の正の平方根である
・帰無仮説は「クラス間の分散が等しい」
・対立仮説は「クラス間の分散が等しくない」
・有意水準5%で等分散性の検定を行う

公式問題集の記述を改変

読み解き

条件から統計的仮説検定の主題を読み解きます。

• 条件より等分散性の検定、つまり「２標本の母分散の比の$${F}$$検定」を行います。

• 検定統計量$${F}$$を用います。

• 対立仮説「クラス間の分散が等しくない」（クラスAの分散≠クラスBの分散）の不等号より、「両側検定」です。

この問題の統計的仮説検定の概要を図示します。

統計的仮説検定の手段

今回は、手計算で検定を実施いたします。

---

手計算で検定

ステップ１：検定統計量$${F}$$を計算する

帰無仮説が正しいと仮定するときの検定統計量 $${F}$$ を計算します。
計算結果の値を「$${F}$$値」と呼びます。
この問題で「帰無仮説が正しいと仮定する」とは、「母分散が等しいので、母分散の比は1である」と仮定することです。

検定統計量$${F}$$の計算式は次のとおりです。

■公式
検定統計量$${F= \cfrac {\hat{\sigma}^2_A / \sigma^2_A}{\hat{\sigma}^2_B/ \sigma^2_B}=\cfrac{\hat{\sigma}^2_A}{\hat{\sigma}^2_B} \cdot \cfrac{\sigma^2_B}{\sigma^2_A}=\cfrac{\hat{\sigma}^2_A}{\hat{\sigma}^2_B} \sim F(n_A-1, n_B-1) }$$

ただし、$${\hat{\sigma}^2_A}$$：クラスAの不偏分散、$${\hat{\sigma}^2_B}$$：クラスBの不偏分散、$${n_A}$$：クラスAの標本サイズ、$${n_B}$$：クラスBの標本サイズ、母分散の比は１と仮定するので$${\cfrac{\sigma^2_B}{\sigma^2_A}=1}$$となる

検定統計量$${F}$$は、自由度$${n_A-1, n_B-1}$$の$${F}$$分布に従います。
分子は値の大きい方の不偏分散、分母は値の小さい方の不偏分散です。
自由度は（分子の標本サイズ－１、分母の標本サイズ－１）です。
分子を目安にして捉えるのです。

問題文で与えられたクラスAの不偏分散$${\hat{\sigma}^2_A=19.5^2}$$、クラスBの不偏分散$${\hat{\sigma}^2_B=14.5^2}$$を用いて検定統計量$${F}$$を計算します。

$$
\begin{align*}
F&= \cfrac{\hat{\sigma}^2_A}{\hat{\sigma}^2_B} \\
 \\
&=\cfrac{19.5^2}{14.5^2} \\
 \\
&=\cfrac{380.25}{210.25} \\
 \\
&=1.808 \cdots \\
&\fallingdotseq 1.81
\end{align*}
$$

解答選択肢（ア）の$${F}$$値は$${1.81}$$です。

ステップ２：$${\boldsymbol{F}}$$分布の両側$${\boldsymbol{2.5\%}}$$点を取得

検定統計量$${F}$$は、自由度（分子の標本サイズ－１, 分母の標本サイズ－１）の$${F}$$分布に従います。
そこで、次の手順で検定を進めます。

• $${F}$$分布のパーセント点表より、自由度と有意水準に合致するパーセント点を取得します。

  • 検定統計量$${F}$$が従う$${F}$$分布の自由度は（20, 40）です。

  • また有意水準$${5\%}$$の両側検定ですので、上側$${2.5\%}$$点と下側$${2.5\%}$$点を取得します。

• 計算した$${F}$$値とパーセント点を比較して仮説を吟味します。

  • 計算した$${F}$$値がパーセント点の区間内の場合に帰無仮説を受容します。
    $${下側2.5\%点 \leq F値 \leq 上側2.5\%点}$$

  • 区間の外の場合には帰無仮説を棄却します。
    $${F値<下側2.5\%点、または、上側2.5\%点 < F値}$$

まず、$${F}$$分布のパーセント点表から、上側$${2.5\%}$$点と下側$${2.5%}$$点を取得します。
次のグラフは上側・下側の$${2.5\%}$$点のイメージです。
左右非対称です。

$${F}$$分布のパーセント点表を見ましょう。
上側確率$${\alpha=0.025}$$の表から、第一自由度$${\nu_1=20}$$、第二自由度$${\nu_2=40}$$の交差点を見ます。
上側$${2.5\%}$$点は$${2.068}$$です。
下の図では、赤い部分が相当します。

下側確率は少々、小技を必要とします。
この表は「上側確率」しか表示していません。
下側確率を取得するには、次のようにします。

①第一自由度と第二自由度を逆にして表を見ます。
逆にすると、第一自由度は$${40}$$、第二自由度は$${20}$$です。
この交差点を見ます。
パーセント点は$${2.287}$$です。
上の図では青い部分が相当します

②取得したパーセント点の逆数を計算します。
下側確率のパーセント点は、①のパーセント点の逆数です。
$${\cfrac{1}{2.287} \fallingdotseq 0.437}$$です。
下側$${2.5\%}$$点は$${0.437}$$です。

ステップ３：$${\boldsymbol{F}}$$値とパーセント点を比較

下側と上側の$${2.5\%}$$点と$${F}$$値の関係は次のようになりました。

$${0.437 \leq 1.81 \leq 2.068}$$

つまり、$${F}$$値$${1.81}$$は下側と上側の$${2.5\%}$$点の区間内にあります。
よって、帰無仮説を棄却しません。

解答選択肢（イ）は　棄却しない　です。

最後に$${F}$$分布のグラフを用いて、$${F}$$検定の結果を可視化しましょう。
$${F}$$値が下側と上側の$${2.5\%}$$点の区間内にあることが分かります。

解答

② です。

難易度　ふつう

・知識：２標本の母分散の比の$${F}$$検定、$${F}$$分布のパーセント点表（特に下側確率の算出）
・計算力：数式組み立て（低）、電卓（低）
・時間目安：1分

実践する

---

EXCELで$${F}$$分布のパーセント点表を作成しましょう。
Pythonでは、$${F}$$検定に簡単に触れた後、記事に用いた図の作成を再現しましょう。

EXCELで作成してみよう！

記事で用いた$${F}$$分布のパーセント点表を作成します。
完成図はこんな感じ。

F分布のパーセント点表

■ F.INV.RT関数
EXCELの関数「F.INV.RT関数」を利用します。
この関数に確率と自由度を与えて、$${F}$$分布の上側パーセント点を取得できます。
引数は F.INV.RT( 確率,  第一自由度,  第二自由度 ) です。

C4セルの上側確率、5行の第一自由度、B列の第二自由度を参照しています。
絶対参照「$」を上の図のように付けることで、数式をコピペしやすくできます。

■ 無限大の対応
$${F}$$分布の第一自由度の最後の列は「無限大」です。
しかし、EXCELは無限大を表現できないようです。
そこで、第一自由度に大きな値「9999999999」を設定して無限大の代用といたしました。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

F分布のパーセント点表.xlsx

17.5 KB

ファイルダウンロードについて

ダウンロード

Pythonで作成してみよう！

最初に、問題で出題された$${F}$$検定について、コードを作成します。
次に、$${F}$$分布の図を作成しましょう。

①インポート

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'

②初期値設定、$${\boldsymbol{F}}$$値算出
２つの標本の標本サイズと標準偏差（不偏分散の正の平方根）の値を設定します。
検定統計量$${F}$$の公式に従って$${F}$$値を計算します。

# 設定
n_1 = 21              # クラスAの標本サイズ
n_2 = 41              # クラスBの標本サイズ
sigma_hat_1 = 19.5    # クラスAの標準偏差（不偏分散の正の平方根）
sigma_hat_2 = 14.5    # クラスBの標準偏差（不偏分散の正の平方根）

# F値の算出
F_value = sigma_hat_1**2 / sigma_hat_2**2
print(f'F値: {F_value:.3f}')

出力イメージ

③$${\boldsymbol{F}}$$検定
有意水準 alpha を設定します。コード例では$${0.05}$$を設定しました。
続いて、自由度、棄却限界値（c_val_lower, c_val_upper）を計算して、$${F}$$値と比較をして、$${F}$$検定の結果を表示します。
「dist = stats.f(df_1, df_2)」とすることで、自由度df_1, df_2の$${F}$$分布のオブジェクトを生成しています。
以後の stats.f の処理を dist に置き換えられるので、記述が簡便になります。

### 初期値設定
# 有意水準の設定
alpha = 0.05
# 自由度の算出
df_1 = n_1 - 1        # 第一自由度
df_2 = n_2 - 1        # 第二自由度

### F分布の棄却域関連値の取得
# 自由度df_1, df_2のF分布のオブジェクト生成
dist = stats.f(df_1, df_2)
# 下側パーセント点の取得
c_val_lower = dist.ppf(alpha / 2)
# 上側パーセント点の取得
c_val_upper = dist.ppf(1 - alpha / 2)

### F検定
if c_val_lower <= F_value <= c_val_upper:
    print(f'{c_val_lower:.3f} <= F値{F_value:.3f} <= {c_val_upper:.3f}より、'
          '帰無仮説は棄却されない')
elif F_value < c_val_lower:
    print(f'F値{F_value:.3f} < 下側{c_val_lower:.3f}より、帰無仮説は棄却される')
elif F_value > c_val_upper:
    print(f'上側{c_val_upper:.3f} < F値{F_value:.3f}より、帰無仮説は棄却される')

出力イメージ

④$${\boldsymbol{F}}$$分布の確率密度関数の描画
$${F分布}$$の確率密度関数、下側・上側の棄却限界値（垂直線）と棄却域（塗りつぶし）などの描画を１つ１つコードで書きます。

### 設定
# グラフのx軸の最小値、最大値
x_min, x_max = 0, 3

### F分布の確率密度関連値の取得
# x軸の値取得
x = np.linspace(x_min, x_max, 1001)
# F分布の確率密度の取得
y = dist.pdf(x)
# 下側確率の確率密度の取得（塗りつぶし用）
x1 = np.linspace(x_min, c_val_lower, 101)
y1 = dist.pdf(x1)
# 上側確率の確率密度の取得（塗りつぶし用）
x2 = np.linspace(c_val_upper, x_max, 101)
y2 = dist.pdf(x2)

### 描画
# 初期値設定（色）
c='steelblue'
# F分布の確率密度関数の描画
plt.plot(x, y, c=c)
# 下側・上側の棄却域の塗りつぶし
plt.fill_between(x1, 0, y1, color=c, alpha=0.3)
plt.fill_between(x2, 0, y2, color=c, alpha=0.3)
# y=0の水平点線の描画
plt.axhline(0, lw=0.5, ls='--', c='black')
# F値の垂直点線の描画
plt.axvline(F_value, ls='--', c='black', label=f'$F$値:{F_value:.2f}')
# 下側パーセント点、上側パーセント点の垂直点線の描画
plt.axvline(c_val_lower, ls='--', c='red',
            label=rf'下側{alpha/2:.1%}点:{c_val_lower:.2f}')
plt.axvline(c_val_upper, ls='--', c='green',
            label=rf'上側{alpha/2:.1%}点:{c_val_upper:.2f}')
# 修飾
plt.title(f'自由度{df_1, df_2}の$F$分布, 有意水準{alpha:.0%}, 両側検定')
plt.xlabel('$F$')
plt.legend()
plt.show()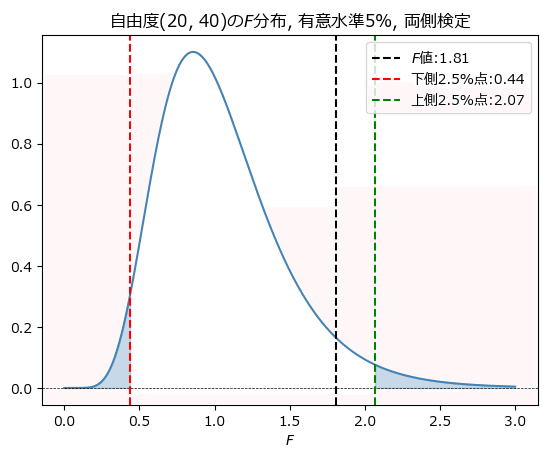

出力イメージ

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

8-9_等分散性の検定.ipynb

99.7 KB

ファイルダウンロードについて

ダウンロード

---

おわりに

$${F}$$分布は２つの自由度をパラメータに持っています。
また、$${F}$$分布の確率密度関数は左右非対称です。
そのため、$${F}$$分布のパーセント点表の表組みが特殊構造になっています。
上側確率しか表現しておらず、かつ、$${5\%}$$と$${2.5\%}$$のみ対応しています。
パソコンを利用すれば、例えばEXCELでは、 F.INV.RT関数（上側パーセント点）、F.INV関数（下側パーセント点）を用いて棄却域をサクッと計算できます。
Pythonでは scipy.stats.f.pptを用いてサクッと計算できます。
そろそろ、紙時代の（低情報量の）パーセント点表から脱皮してもいいような気がします。

最後までお読みいただきまして、ありがとうございました。

---

のんびり統計シリーズの記事

次の記事

前の記事

目次