
【号外その1】第1種の過誤と第2種の過誤のバランス
号外
突然ですが、統計検定2級過去問題をPythonで解いちゃおう!のコーナーです。
統計的仮説検定における第1種の過誤・第2種の過誤の関係をPythonで可視化します。
📘公式問題集
統計検定2級 2019年6月 問16(回答番号28~30)
Pythonで解く
問題① 第1種の過誤・第2種の過誤の確率
棄却域を$${x \geq 0.8}$$とするときの第1種の過誤・第2種の過誤の確率を求めます。
「帰無仮説$${H0}$$で仮定する正規分布$${N(0,1)}$$」と「対立仮説で仮定する正規分布$${N(1,1)}$$」と「棄却限界値$${x=0.8}$$」が交錯するグラフをお楽しみください。
Pythonコード①
インポート
### インポート
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'帰無仮説H0と対立仮説H1の確率分布の設定
scipy.stats の normオブジェクトH0、H1を生成します。
loc で平均、scale で標準偏差を指定します。
### 設定
# 帰無仮説H0と対立仮説H1の確率分布
H0 = stats.norm(loc=0, scale=1)
H1 = stats.norm(loc=1, scale=1)帰無仮説と対立仮説の可視化
3つのグラフをプロットします。
・$${H_0}$$の分布・$${H_1}$$の分布・棄却限界値
・$${H_0}$$の分布・第1種の過誤の確率$${\alpha}$$
・$${H_1}$$の分布・第2種の過誤の確率$${\beta}$$
第1種の過誤の確率$${\alpha}$$は、棄却限界値$${0.8}$$の上側確率を norm.sf で取得します。
第2種の過誤の確率$${\beta}$$は、棄却限界値$${0.8}$$の下側確率を norm.cdfで取得します。
### 帰無仮説と対立仮説の可視化
# 棄却限界値
critical_value = 0.8
## H0とH1の正規分布の確率密度関数を取得
x = np.linspace(-5, 5, 1001)
y_H0 = H0.pdf(x)
y_H1 = H1.pdf(x)
### プロット
fig, ax = plt.subplots(1,3, figsize=(10, 3), sharex=True, sharey=True)
## H0の分布、H1の分布、棄却限界値のプロット
ax[0].plot(x, y_H0, color='steelblue', label='H0')
ax[0].plot(x, y_H1, color='orange', label='H1')
ax[0].axvline(critical_value, ls='--', color='red', label=critical_value)
ax[0].axhline(0, lw=0.5, ls='--', color='black')
ax[0].legend()
## H0の分布、棄却域、αの値のプロット・表示
# 棄却域塗りつぶし用
x1 = np.linspace(critical_value, 5, 101)
y1_H0 = H0.pdf(x1)
# 第1種の過誤αの確率
alpha = H0.sf(critical_value)
# プロット
ax[1].plot(x, y_H0, color='steelblue', label='H0')
ax[1].fill_between(x1, y1_H0, 0, color='steelblue', alpha=0.3, label=f'$\\alpha$')
ax[1].axvline(critical_value, ls='--', color='red', label=critical_value)
ax[1].axhline(0, lw=0.5, ls='--', color='black')
ax[1].set_title('$H0:\\theta=0, X \sim N(0,1)$\n'
f'$\\alpha={alpha:.3f}$')
ax[1].legend(loc='upper left')
## H1の分布、棄却域、βの値のプロット・表示
# 第2種の過誤塗りつぶし用
x2 = np.linspace(-5, critical_value, 101)
y2_H1 = H1.pdf(x2)
# 第2種の過誤βの確率
beta = H1.cdf(critical_value)
# プロット
ax[2].plot(x, y_H1, color='orange', label='H1')
ax[2].fill_between(x2, y2_H1, 0, color='orange', alpha=0.3, label=f'$\\beta$')
ax[2].axvline(critical_value, ls='--', color='red', label=critical_value)
ax[2].axhline(0, lw=0.5, ls='--', color='black')
ax[2].set_title('$H1:\\theta=1, X \sim N(1,1)$\n'
f'$\\beta={beta:.3f}$')
ax[2].legend()
plt.show()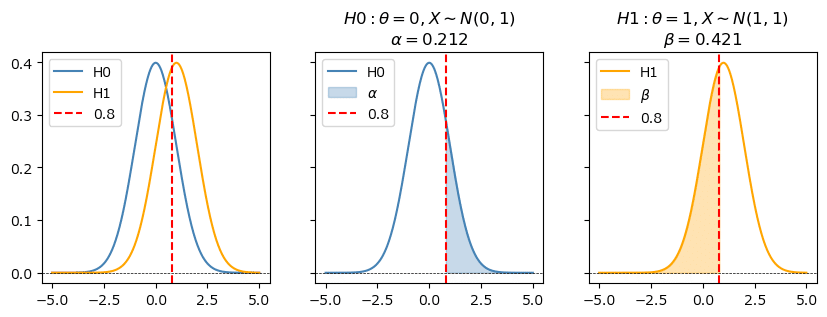
問題② 第1種の過誤・第2種の過誤の確率の可視化
棄却域を$${x \geq x_0}$$とするとき、(1-第2種の過誤の確率、第1種の過誤の確率)をグラフにプロットします。
そして、第1種の過誤の確率と第2種の過誤の確率の和を最小にする$${x_0}$$を探します。
Pythonコード②
第1種の過誤の確率$${\alpha(x_0)}$$と第2種の過誤の確率$${\beta(x_0)}$$を用いて可視化してまいります!
変数 x0 に0~1の間の値を101個用意します。
alpha_x0 には x0の範囲で帰無仮説$${H_0}$$の従う分布の確率密度を設定します。
beta_x0 には x0の範囲で帰無仮説$${H_1}$$の従う分布の確率密度を設定します。
2番め、3番めのグラフで$${\alpha(x_0)+\beta(x_0)}$$の最小値をご確認ください。
### 第1種の過誤の確率α、第2種の過誤の確率βの可視化
# x0が0~1のときのα(x0)、β(x0)を取得
x0 = np.linspace(0, 1, 101)
alpha_x0 = H0.sf(x0)
beta_x0 = H1.cdf(x0)
fig, ax = plt.subplots(1, 3, figsize=(10, 4))
# β(x0), 1-α(x0)のプロット
ax[0].plot(beta_x0, 1-alpha_x0)
ax[0].set_xlabel('$\\beta(x_0)$')
ax[0].set_ylabel('$1-\\alpha(x_0)$')
ax[0].set_title('$\\beta(x_0), 1-\\alpha(x_0)$のプロット')
# x0とα(x0), β(x0)のプロット
ax[1].plot(x0, alpha_x0, label='$\\alpha(x_0)$')
ax[1].plot(x0, beta_x0, label='$\\beta(x_0)$')
ax[1].set_xlabel('$x_0$')
ax[1].set_ylabel('確率')
ax[1].set_title('$\\alpha(x_0)$と$\\beta(x_0)$の確率')
ax[1].legend(loc='upper center')
# x0とα(x0)+β(x0)のプロット
ax[2].plot(x0, alpha_x0 + beta_x0, color='green',
label='$\\alpha(x_0)+\\beta(x_0)$')
ax[2].set_xlabel('$x_0$')
ax[2].set_ylabel('確率')
ax[2].set_title('$\\alpha(x_0)+\\beta(x_0)$の確率')
ax[2].legend(loc='upper center')
plt.suptitle('棄却域 $x \geq x_0, x_0=[0,1]$ のときの$\\alpha(x_0),'
'\\beta(x_0)$の可視化')
plt.tight_layout()
plt.show()
Pythonコード③
$${\alpha(x_0)+\beta(x_0)}$$が最小になるときの棄却限界値$${x_0=0.5}$$を用いて、Pythonコード①と同じコードを流してみます。
棄却限界値と過誤の確率の動きを確認してみましょう!
$${\alpha}$$と$${\beta}$$が仲良く同じ確率になりました。
### 帰無仮説と対立仮説の可視化
# 棄却限界値
critical_value = 0.5
## H0とH1の正規分布の確率密度関数を取得
x = np.linspace(-5, 5, 1001)
y_H0 = H0.pdf(x)
y_H1 = H1.pdf(x)
### プロット
fig, ax = plt.subplots(1,3, figsize=(10, 3), sharex=True, sharey=True)
## H0の分布、H1の分布、棄却限界値のプロット
ax[0].plot(x, y_H0, color='steelblue', label='H0')
ax[0].plot(x, y_H1, color='orange', label='H1')
ax[0].axvline(critical_value, ls='--', color='red', label=critical_value)
ax[0].axhline(0, lw=0.5, ls='--', color='black')
ax[0].legend()
## H0の分布、棄却域、αの値のプロット・表示
# 棄却域塗りつぶし用
x1 = np.linspace(critical_value, 5, 101)
y1_H0 = H0.pdf(x1)
# 第1種の過誤αの確率
alpha = H0.sf(critical_value)
# プロット
ax[1].plot(x, y_H0, color='steelblue', label='H0')
ax[1].fill_between(x1, y1_H0, 0, color='steelblue', alpha=0.3, label=f'$\\alpha$')
ax[1].axvline(critical_value, ls='--', color='red', label=critical_value)
ax[1].axhline(0, lw=0.5, ls='--', color='black')
ax[1].set_title('$H0:\\theta=0, X \sim N(0,1)$\n'
f'$\\alpha={alpha:.3f}$')
ax[1].legend(loc='upper left')
## H1の分布、棄却域、βの値のプロット・表示
# 第2種の過誤塗りつぶし用
x2 = np.linspace(-5, critical_value, 101)
y2_H1 = H1.pdf(x2)
# 第2種の過誤βの確率
beta = H1.cdf(critical_value)
# プロット
ax[2].plot(x, y_H1, color='orange', label='H1')
ax[2].fill_between(x2, y2_H1, 0, color='orange', alpha=0.3, label=f'$\\beta$')
ax[2].axvline(critical_value, ls='--', color='red', label=critical_value)
ax[2].axhline(0, lw=0.5, ls='--', color='black')
ax[2].set_title('$H1:\\theta=1, X \sim N(1,1)$\n'
f'$\\beta={beta:.3f}$')
ax[2].legend()
plt.show()
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
この問題は帰無仮説の分布と対立仮説の分布を可視化することで、問題の意味・意図をつかみやすくなると思います!
ちなみに「問題②」の一部分は、公式問題集CBT対応版に記載されています。
のんびり統計「8-10(β, 1-α)のグラフ」で取り上げる予定です!
最後までお読みいただきまして、ありがとうございました。
ブログの紹介
noteで3つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
3.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、、Pythonのコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
この記事が気に入ったらサポートをしてみませんか?
