【改】第12章「顔は口ほどではないが嘘を言う」のベイズモデリングをPyMC Ver.5 で

2023年12月20日 11:56

プロローグ

この記事は、以前投稿した『テキスト「たのしいベイズモデリング」の第12章「顔は口ほどではないが嘘を言う」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。』を改造する記事です。

以前の記事はこちらです。

上記記事の執筆時点では、PyMCモデルを描くことができなくて「棄権する」という苦い思いをしました。
ところが姉妹書「たのしいベイズモデリング２」第８章のPyMC実装を楽しんでいる最中に、こんな啓示が降りてきたのです。

『テキストをじっくり読めば、ヒントが見つかるかもしれないよ！』

テキストとRスクリプトをじっくり読みました。
あ！

２つのモデルのうち、最初の信号検出理論（SDT）の実装方法の調べ方と作業ステップのイメージが見えました！
アレが使えそうです。アレです🦌

そしてそして・・・
信号検出理論のブログを書き終えたときに、ふとテキストを見やると・・・
ベータ多項過程ツリーモデルの数式がPyMCのモデルへと繋がったのです！
ラッキー！天からの贈り物かしら？
サンタさん、ありがとうございます！

ということで、新装開店、PyMCモデリングを開始いたします！
それではテイクツー、スタートです！

リスタート

この記事は、テキスト「たのしいベイズモデリング」の第12章「顔は口ほどではないが嘘を言う」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。

今回は、テキスト記述内容・データセット・Rスクリプト等が一見複雑に見える「難解の壁」が立ちはだかり、初学者に厳しい虎の穴的なモデルです。
ですので、根本の理解を断念することにして、数式とデータ項目とRスクリプト（プログラムコード）を手がかりに「PyMC5モデルがひとまず動くレベル」を目指します。

では、PyMCのベイズモデリングを楽しんでいきましょう！

テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。

テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。

サマリー

テキストの概要

執筆者　　　：　難波修史先生
モデル難易度：　★★★★★　（難しい）

自己評価

評点

$$
\begin{array}{c:c:c}
実装精度 & ★★★★・& ほぼ納得 \\
結果再現度 & ★★★★・& あと一歩 \\
楽しさ & ★★★★★& 楽しい！ \\
\end{array}
$$

評価ポイント

brmsにてR風のformula形式で書かれた信号検出理論モデルを解読できました！
そしてformulaベースのPyMCモデリングを経て、推論データの動きが見えてくるにつれて、テキストの数式モデルで書かれた信号検出理論モデルを解読できるようになりました！
ベータ多項過程ツリーモデルはRやTreeBUGSコードを無視して、「テキストの数式モデル」を信じてPyMC化したところ、テキストと近い結果が得られました！

工夫・喜び・反省

一度は棄権という苦汁をなめましたが、一歩前進できたことをとても嬉しく思います。
brmsのモデリングに用いられた「R風のformula形式」モデルは、PyMC用の「Bambi」で対応できました。

モデルの概要

テキストの調査・実験の概要

■ 体験表情と意図表情
「嬉しい、ありがとう」と彼が喜んでいます。
体験に基づく感情（注）から生まれる嘘偽りのない表情、それとも、体験したふりをして意図的に作り出した偽りの表情。
彼の表情はどちらでしょう・・・
「顔は口ほどではないが嘘を言う」の幕開けです。

テキストは、他人の表情に見える感情が「体験から生じた本物か」、「ふりをした偽物か」を人が正確に「検出」できるのかに注目しています。
まえがきの文章をお借りします。

実際我々は、他者による情動（注）体験の存在を正確に検出できるのか。この問いを明らかにするため、本章では情動体験から自然に生じた表情（体験表情）と意図的に作成した特定の情動を体験している”ふり”の表情（意図表情）を弁別できるかを検討する。

テキストより引用

（注）テキストでは情動と感情を区別して用いていますが、読みやすさを優先してこのブログでは「感情」に統一して記述しています。

■ 実験の概要
実験参加者30名が映像に映る人の表情を見て、体験表情と判断する場合は「はい」、体験表情ではないと判断する場合は「いいえ」を回答します。
実験参加者は「感情４種類 × 体験表情・意図表情・無表情 × 映像出演者２人＝２４パターン」の映像上の表情を判断しています。
モデリングに使用するデータには、無表情への回答を除いた16パターン×30人＝480データが含まれます。

図示します。

テキストのモデリング

テキストは２つのモデルでベイズ推論を行っています。

① 等分散を仮定した信号検出理論の階層モデル（SDTモデル）

■ モデルの概念図
テキストの図12.2をお借りします。
標準正規分布を用いて「体験なし分布」「体験なし分布」を表現し、関心のあるパラメータ「判断基準$${c}$$、信号検出力$${d}$$、反応バイアス」の関係を示しています。

実験参加者が映像の表情を見て「体験がある」と反応するときの基準線が、判断基準$${c}$$です。
表情から判断基準$${c}$$以上の信号を受け取ったとき、「はい」（体験表情です）と回答するのです。

■ 目的変数と関心のあるパラメータ
目的変数は、体験表情かどうかを「1:はい」「0:いいえ」で記録した回答$${y_{ij}}$$です。
関心のあるパラメータは、実験参加者$${i}$$の①判断基準$${c_i}$$の平均$${\mu_c}$$と②信号検出力$${d_i}$$の平均$${\mu_d}$$、③$${c_i,\ d_i}$$の相関係数$${\rho}$$、④反応バイアスです。
添字$${j}$$は試行番号です。

$$
\begin{align*}
y_{ij} &\sim \text{Bernoulli}\ (p_{ij}) \\
p_{ij} &= \Phi\ (\eta_{ij}) \\
\eta_{i} &= A_i + B_i \times Display_{ij} \\
A_i &= -c_i,\ B_i = d_i \\
\left[ \begin{matrix} c_i \\ d_i\end{matrix}\right] &\sim
\text{BivariateNormal}\ \left(
\left[ \begin{matrix} \mu_c \\ \mu_d \end{matrix} \right],
\left[ \begin{matrix} \sigma_c \\ \sigma_d \end{matrix} \right],
\rho \right) \\
\end{align*}
$$

テキストより引用

目的変数$${y_{ij}}$$は確率$${p_{ij}}$$をパラメータに持つベルヌーイ分布に従います。
$${\Phi}$$はプロビット変換であり、標準正規分布に従う$${\eta_{ij}}$$を確率$${p_{ij}}$$に変換します。
$${\eta_{ij}}$$は説明変数$${Display}$$（映像の表情が0:意図表情か1:体験表情かを示す変数）を用いた回帰式です。
切片$${A_i}$$は判断基準$${c_i}$$のマイナス値、傾き$${B_i}$$は信号検出力$${d_i}$$と一致するそうです。
$${\text{BivariateNormal}}$$は２変量正規分布です。

パラメータの意味合いの詳細はテキストをご覧ください。
なお、上記数式に含まないパラメータの事前分布は、テキストやRスクリプトに明示されていません。

② ベータ分布を用いた多項過程ツリーの階層モデル（MPTモデル）

■ モデルの概念
体験表情に対する反応と意図表情に対する反応について、正否の結果をテキストでは反応カテゴリーと呼んでいます。
反応カテゴリーには「ヒット・ミス・誤警報・正棄却」が含まれます。
表情の種類・判断・反応カテゴリーの関係は次のとおりです。

$$
\begin{array}{l|ll}
判断（回答） & 表情の種類 & （正解値） \\
\hdashline
& 体験表情 & 意図表情\\
\hline
体験表情である（はい） & ヒット & 誤警報 \\
意図表情である（いいえ） & ミス & 正棄却 \\
\end{array}
$$

このような反応カテゴリーが生じるメカニズムとして、テキストは「２高閾モデル」を用います。
判断の過程で２段階のしきい値が用いられます。
主要なパラメータは３つ。

１．体験弁別パラメータ$${r}$$
体験表情が感動した体験に基づくものだと確信して弁別（識別）できる確率

２．意図弁別パラメータ$${d}$$
意図表情が体験に基づかないものだ（ふりをしているだけだ）と確信して弁別できる確率

３．推測パラメータ$${g}$$
体験表情の識別、意図表情の識別がハッキリしない場合・うまく識別できない場合に「体験表情である」と推測する確率

他者の表情を起点にして、最初に体験弁別パラメータ$${r}$$・意図弁別パラメータ$${d}$$が発動して体験表情か否かを判断します。
最初の弁別ができない場合に、推測パラメータ$${g}$$が登場して体験表情か否かを推測します。

３つのパラメータの働きと反応カテゴリーとの関連については、テキストの図12.3の概念図がとても分かりやすいので、お借りいたしました。

■ 目的変数と関心のあるパラメータ
目的変数は、実験参加者$${i}$$ごとの16問題（試行）の内数「ヒット数・ミス数・誤警報数・正棄却数」のセット$${k_{i}}$$です。
関心のあるパラメータは、体験弁別パラメータ$${r_i}$$の平均$${\mu_r}$$・標準偏差$${\sigma_r}$$と、推測パラメータ$${g_i}$$の平均$${\mu_g}$$・標準偏差$${\sigma_g}$$です。

$$
\begin{align*}
k_i &\sim \text{Multinomial}\ (\theta_i) \\
\theta_i &= (p_{ヒットi},\ p_{ミスi},\ p_{誤警報i},\ p_{正棄却i}) \\
p_{ヒットi} &= r_i + (1 - r_i) \times g_i \\
p_{ミスi} &= (1 - r_i) \times (1 - g_i) \\
p_{誤警報i} &= (1 - d_i) \times g_i \\
p_{正棄却i} &= d_i + (1 - d_i) \times (1 - g_i) \\
r_i &\sim \text{Beta}\ (\alpha_{ri},\ \beta_{ri}) \\
d_i &= r_i \\
g_i &\sim \text{Beta}\ (\alpha_{gi},\ \beta_{gi}) \\
\alpha_{ri},\ \alpha_{di},\ \alpha_{gi} &\sim \text{Gamma}\ (1,\ 0.1) \\
\beta_{ri},\ \beta_{di},\ \beta_{gi} &\sim \text{Gamma}\ (1,\ 0.1) \\
\mu &= \cfrac{\alpha}{\alpha + \beta} \\
\sigma &= \cfrac{\sqrt{\alpha \beta}}{(\alpha+\beta) \times \sqrt{\alpha+\beta+1}} \\
\end{align*}
$$

テキストを一部改変して引用

$${\mu,\ \sigma}$$の計算式は、ベータ分布の平均・標準偏差の計算方法によります。

なお、テキストではモデルの分析不能状態を回避する目的で、パラメータ$${r,d}$$との間に次のような制約を採用しています。

$${r=d}$$：確信を持って体験を弁別するパラメータが表情で異ならない

テキストより引用

■ 分析・分析結果
分析結果はテキストに記載の図表を利用して実施して下さい。
PyMCモデリングでの分析結果は、「PyMC実装」章の【分析】の部分をご覧ください。

PyMC実装「等分散を仮定した信号検出理論の階層モデル」

Let's enjoy PyMC & Python !

「等分散を仮定した信号検出理論の階層モデル」に取り組みます。

準備・データ確認

１．インポート

### インポート

# ユーティリティ
import pickle

# 数値・確率計算
import pandas as pd
import numpy as np

# PyMC
import pymc as pm
import pytensor.tensor as pt
import bambi as bmb
import arviz as az

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

２．データの読み込み
csvファイルをpandasのデータフレームに読み込みます。

### データの読み込み
# 項目説明
#  Feel:表情の種類（0:意図表情、1:体験表情）, expressrer:不明, emotion:感情の種類,
#  eva:体験表情かどうかの回答（0:いいえ、1:はい）,
#  obs:実験参加者ID, sex:性別, age:年齢

# データの読み込み
data = pd.read_csv('Tai.csv')

# # option:信号タイプの設定（必要に応じて）
# dic = {(0, 0):'正棄却', (0, 1):'誤警報', (1, 0):'ミス', (1, 1):'ヒット'}
# data['signal'] = data[['Feel', 'eva']].apply(
#                                 lambda x: dic[x.iloc[0], x.iloc[1]], axis=1)

# データの表示
display(data)

【実行結果】
全480行です。
モデリングに利用する項目は次のとおりです。
・Feel：表情の種類（0:意図表情、1:体験表情）
・eva：体験表情かどうかの回答（0:いいえ、1:はい）※目的変数
・obs：実験参加者ID

３．データの外観・統計量
ひとまず要約統計量を確認します。

### 要約統計量の表示
data.describe().round(3)

【実行結果】
・・・、よく分かりませんね。

意図表情・体験表情ごとに「体験表情」と回答した比率を描画します。
テキストの図12.1に相当します。
seaborn の barplot を利用します。黒線は95%信頼区間です。

### 体験表情と答えた比率の描画 ※図12.1に相当
ax = sns.barplot(data=data, x='Feel', y='eva', color='lightpink', width=0.5,
                 err_kws={'linewidth': 1}, )
ax.set(xticks=[0, 1], xticklabels=['意図表情', '体験表情'],
       xlabel='表情の種類', ylabel='体験表情と答えた比率');

【実行結果】

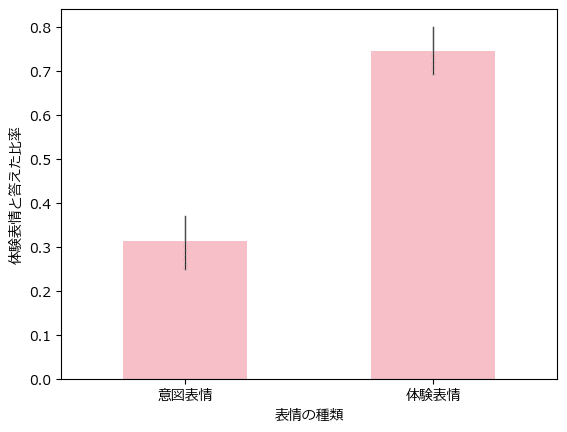
意図的に作り出した表情である「意図表情」を見て、体験表情だと回答した比率が30%ほどあります。
３割くらいのケースで「騙されている」ことになります。
また、自然に湧き出た表情である「体験表情」を見て、体験表情ではないと回答した比率は25%ほどあります。
４分の１のケースで表情を「わざとらしい」と感じていることになります。

この棒グラフを深掘りしましょう。
まずは、感情別に分割してみます。

### 体験表情と答えた比率の描画　感情の種類別（幸福・嫌悪・驚き・悲しみ）
ax = sns.barplot(data=data, x='Feel', y='eva', hue='emotion', palette='Pastel1',
                 gap=0.1, err_kws={'linewidth': 1})
ax.set(xticks=[0, 1], xticklabels=['意図表情', '体験表情'],
       xlabel='表情の種類', ylabel='体験表情と答えた比率')
ax.legend(title='感情の種類');

【実行結果】
感情の種類コード値0～3と感情名「幸福・嫌悪・悲しみ・驚き」の組み合わせが不明のため、ここではコード値で書きます。

左の群は意図表情のことを体験表情であると誤る比率です。
20～40%程度の誤り、つまり、意図した表情に騙された様子が分かります。
特に紫の3番の感情は騙されやすいようです（驚きの感情でしょうか？）。

一方、右の群は体験表情のことを体験表情であると正しく回答した比率です。
70～85%程度の正解、逆に言うと、15～30%程度の誤りがありそうです。
特に緑の2番の感情は作り出した顔だ・わざとらしいと勘違いされやすいようです（悲しみの感情でしょうか？）。

続いて実験参加者ID別に見てみましょう。

### 体験表情と答えた比率の描画　実験参加者別
plt.figure(figsize=(12, 5))
ax = sns.barplot(data=data, x='Feel', y='eva', hue='obs', palette='Pastel1',
                 err_kws={'linewidth': 0.5}, legend=None)
ax.set(xticks=[0, 1], xticklabels=['意図表情', '体験表情'],
       xlabel='表情の種類', ylabel='体験表情と答えた比率');

【実行結果】
参加者の癖が出ますね！
例えば、左端の赤い棒に該当する人は、意図表情のことを体験表情だと騙された比率が80%近いです！
また、どの棒も95%信頼区間を示すヒゲが長いです。
個人レベルに細かくすると、正解のばらつきが大きくなるようです。

では、テキストの「等分散を仮定した信号検出理論の階層モデル」をPyMCで実装しましょう！

モデル１：Bambiで記述

Rコードにbrmsのモデル定義式を見つけました。
コードの一部を引用いたします。

# brm(回帰式, 誤差構造の設定, データ)
# 回帰式中の(1|ID)は切片の,(Feel|ID)は傾きの変量効果を指定。
fitF <- brm(eva ~ 1 + Feel + (1 + Feel | obs), 
              family = bernoulli(link="probit"), data = Tai)

特に「eva ~ 1 + Feel + (1 + Feel | obs)」に注目です。
R言語の回帰式のformula構文ではありませんか！
ということは、PyMCですと・・・

「Bambi」の出番です！

Bambi は formula構文で記述したモデルをPyMCで動かせるパッケージです。
次のサイトはBambi公式の「はじめよう」のページです。

１．モデルの定義
brmsのモデル定義式をそのまま用いて、Bambiのモデルを定義しましょう。

### モデルの定義
model_bmb = bmb.Model(
        formula='eva ~ 1 + Feel + (1 + Feel | obs)',   # フォーミュラ式
        data=data,                                     # データ
        family='bernoulli',                            # 目的変数の分布
        link='probit',                                 # リンク関数
)

【モデル注釈】

formula引数でformula構文を書きます。クォーテーションで括ります。
- ~ の左側
  データフレームdataの目的変数を指定します。
  このモデルでは「eva」（体験表情かどうかの回答）を指定しています。
- ~ の右側
  - 「1」は切片（Intercept）の平均のことを示しています。
    判断基準$${c_i}$$の平均値$${mu_c}$$に相当すると思われます。
  - 「Feel」は説明変数「Feel」の回帰係数の平均です。
    信号検出力$${d_i}$$の平均値$${mu_d}$$に相当すると思われます。
  - ( 1 + Feel | obs )・・・obsは実験参加者IDです。
    - 「1 | obs」は実験参加者IDごとの切片への効果（変量効果）です。
    - 「Feel | obs」は実験参加者IDごとの回帰係数への効果（変量効果）です。
data引数にデータフレームdataを指定します。
family引数に目的変数「eva」（の誤差）が従う確率分布を指定します。
このモデルではベルヌーイ分布を指定しています。
link引数にリンク関数を指定します。
このモデルではプロビット（probit）を指定しています。

brmsのモデル定義がBambiのモデル記述方法と似ていてよかったです！

２．モデルの外観の確認

# モデルの表示
model_bmb

【実行結果】
いろんな情報が出てきました！

target=Pの部分は（おそらく）ベルヌーイ分布のパラメータ$${p}$$をプロビット変換する前の「回帰式」の目的変数（つまり eva）のことだと思われます。
以降に回帰式のパラメータの事前分布が記載されています。
すべて、平均0の正規分布に従っています。
Common-level effects は固定効果でしょうか？共通的なパラメータです。
Interceptはformula構文の「1」で定義したものです。
Group-level effects は変量効果でしょうか？
ここではobs、つまり実験参加者IDごとの効果のパラメータです。
正規分布の標準偏差は半正規分布に従っています。

モデルを可視化します。
モデルに対して「build()メソッド」実行後（またはfit()メソッド実行後）に、「graph()メソッド」を用いてモデルを可視化できます。

### モデルの可視化
model_bmb.build()
model_bmb.graph()

【実行結果】
offset が出てきました（これは何者？）

３．事後分布からのサンプリング
乱数生成数（draws, tune, chains）はテキストに明記されていない（おそらくbrms等のデフォルト値を採用）ため、適当な値を設定しています。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ1分でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　1分
idata_bmb = model_bmb.fit(draws=1000, tune=1000, chains=4, target_accept=0.8, 
                          nuts_sampler='numpyro', random_seed=1234)

【実行結果】省略

４．サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。

### r_hat>1.1の確認
# 設定
idata_in = idata_bmb     # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】
このモデルは$${\hat{R} \leq 1.01}$$をクリアしています。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

事後分布の要約統計量とプロットトレースを確認します。

### 推論データの要約統計情報の表示
pm.summary(idata_bmb, hdi_prob=0.95, round_to=3)

【実行結果】

### トレースプロットの表示
pm.plot_trace(idata_bmb, compact=True)
plt.tight_layout();

【実行結果】
きれいな形状ですね！収束している感じがいたします。

判断基準の平均$${\mu_c}$$、信号検出力の平均$${\mu_d}$$、判断基準の標準偏差$${\sigma_c}$$、信号検出力の標準偏差$${\sigma_d}$$を確認します。
テキストの表12.2の平均・SDに相当します。

テキストがHDI区間を採用しているので、pm.summary() の値をそのまま使います。
ただし、Bambiモデルで推論したパラメータと上記のパラメータの紐付け方が不明瞭なため、次のように仮紐付けしております。

$$
\begin{array}{ll}
テキストのパラメータ & \text{Bambi}モデルのパラメータ\\
\hline
判断基準の平均\ \mu_c & \text{Intercept} \\
信号検出力の平均\ \mu_d & \text{Feel} \\
判断基準の標準偏差\ \sigma_c & \text{1|obs\_sigma} \\
信号検出力の標準偏差\ \sigma_d & \text{Feel|obs\_sigma} \\
\end{array}
$$

### 信号検出理論による結果：要約統計量　※表12.2の平均・SDに相当
var_names = ['Intercept', 'Feel', '1|obs_sigma', 'Feel|obs_sigma']
pm.summary(idata_bmb, hdi_prob=0.95, var_names=var_names, kind='stats',
           round_to=3)

【実行結果】
上から$${\mu_c,\ \mu_d,\ \sigma_c,\ \sigma_d}$$です。
Interceptは正負（プラスマイナス）が逆転しています。
テキストの結果と近い感じがします。

【分析～テキストにならって】
信号検出力（Feel、たぶん$${\mu_d}$$）の値より、体験に基づく感情の表情を見分けることができたと考えられ、特に95%HDI区間が0より離れているので検出力が大きい、と読めるようです。

モデル２：BambiモデルをPyMCで模写する

以下のBambiのモデルをPyMCのモデルで記述してみます。

１．モデルの定義

### モデルの定義
with pm.Model() as model_sdt1:
    
    ### データ関連定義
    ## coordの定義
    # データ全体のインデックス
    model_sdt1.add_coord('data', values=data.index, mutable=True)
    # 実験参加者ID
    model_sdt1.add_coord('id', values=sorted(data['obs'].unique()),
                        mutable=True)    
    ## dataの定義
    # 目的変数：映像の表情が体験表情か否かの回答（0:いいえ、1:はい）
    y = pm.ConstantData('y', value=data['eva'], dims='data')
    # 説明変数：映像の表情が意図か体験かの正解値（0:意図表情、1:体験表情）
    Display = pm.ConstantData('Display', value=data['Feel'].values, dims='data')
    # 実験参加者IDのインデックス
    idIdx = pm.ConstantData('idIdx', value=data['obs'].values -1, dims='data')

    ### 事前分布
    ## c:判断基準、d:信号検出力
    # c,dの平均
    muC = pm.Normal('muC', mu=0, sigma=3.5355)  # sigma=3.5355
    muD = pm.Normal('muD', mu=0, sigma=5)
    # 実験参加者ごとのc,dの変量効果の標準偏差
    sigmaC = pm.HalfNormal('sigmaC', sigma=3.5355)  # sigma=3.5355
    sigmaD = pm.HalfNormal('sigmaD', sigma=5)
    # 実験参加者ごとのc,dの変量効果
    obsC = pm.Normal('obsC', mu=0, sigma=sigmaC, dims='id')
    obsD = pm.Normal('obsD', mu=0, sigma=sigmaD, dims='id')
    # 実験参加者ごとのc,d
    c = pm.Deterministic('c', muC + obsC, dims='id')
    d = pm.Deterministic('d', muD + obsD, dims='id')
    
    # η：表情の種類Displayによる傾きと切片の線形結合
    eta = pm.Deterministic('eta', -c[idIdx] + d[idIdx] * Display, dims='data')
    # 確率p：pm.invprobit(η)でηをプロビット変換
    p = pm.Deterministic('p', pm.math.invprobit(eta), dims='data')

    ### 尤度
    likelihood = pm.Bernoulli('likelihood', p=p, observed=y, dims='data')
    
    ### 計算値
    # 反応バイアス：体験なし分布が標準正規分布N(0,1)であると仮定
    resBias = pm.Deterministic('resBias',  c - d/2, dims='id')

【モデル注釈】
Bambiモデルで不明瞭な部分はテキストの数式モデルで補完してみました（補完したつもり・・・）。
プロット変換には、pymc.math の invprobit() を利用しています。

２．モデルの外観の確認

### モデルの表示
model_sdt1

【実行結果】
注目するパラメータは muC、muD、sigmaC、sigmaD です。

モデルを可視化します。

### モデルの可視化
pm.model_to_graphviz(model_sdt1)

【実行結果】
判断基準$${c_i}$$と信号検出力$${d_i}$$はそれぞれ別個に、単変量正規分布に従っています。
テキストの数式モデルでは$${c_i}$$と$${d_i}$$の相関を想定して、２変量正規分布に従うものとしている点が異なります。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　20秒
with model_sdt1:
    idata_sdt1 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8, 
                           nuts_sampler='numpyro', random_seed=1234)

【実行結果】省略

### r_hat>1.1の確認
# 設定
idata_in = idata_sdt1    # idata名
threshold = 1.05         # しきい値

# しきい値を超えるR_hatの個数を表示
(az.rhat(idata_in) > threshold).sum()

【実行結果】
このモデルは$${\hat{R} \leq 1.05}$$をクリアしています。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

事後分布の要約統計量とプロットトレースを確認します。

### 推論データの要約統計情報の表示
pm.summary(idata_sdt1, hdi_prob=0.95, round_to=3)

【実行結果】

### トレースプロットの表示
pm.plot_trace(idata_sdt1, compact=True)
plt.tight_layout();

【実行結果】
きれいな形状ですね！収束している感じがいたします。

判断基準の平均$${\mu_c}$$、信号検出力の平均$${\mu_d}$$、判断基準の標準偏差$${\sigma_c}$$、信号検出力の標準偏差$${\sigma_d}$$、$${c}$$と$${d}$$の相関$${\rho}$$を確認します。
テキストの表12.2の平均・SD・相関に相当します。
なお、相関係数$${\rho}$$の計算方法をテキストおよびRスクリプトで把握できなかったため、30名の参加者の$${c_i}$$と$${d_i}$$の相関係数を用いました。

### 信号検出理論による結果：要約統計量　※表12.2の平均・SD・相関に相当

## 相関係数の算出
# 推論データからc,dの取り出し
c = idata_sdt1.posterior.c.stack(sample=('chain', 'draw')).data
d = idata_sdt1.posterior.d.stack(sample=('chain', 'draw')).data
# 相関係数の算出 NumPyのcorrcoef()関数を利用して実験参加者30名の相関を計算
rhos = []
for i in range(c.shape[1]):
    rhos.append(np.corrcoef(c[:, i], d[:, i])[0][1])
# 相関係数の事後統計量の算出
rho = (np.mean(rhos), np.std(rhos), np.quantile(rhos, 0.025),
       np.quantile(rhos, 0.975))

## 平均、標準偏差の事後統計量の算出
var_names = ['muC', 'muD', 'sigmaC', 'sigmaD']
summary1 = pm.summary(idata_sdt1, hdi_prob=0.95, var_names=var_names,
                      kind='stats', round_to=3)
## データフレーム化 
summary1 = pd.concat(
    [summary1, pd.DataFrame(rho, index=summary1.columns, columns=['rho']).T],
    axis=0)
display(summary1.round(3))

【実行結果】
Bambiモデルを模写したつもりでしたが、事後統計量は若干違います（汗）
ですが、こちらの事後統計量もテキストの結果と近い感じがします！

ただし、相関係数 rho はテキストと全く違います（テキストよりも区間幅が狭い）。
相関係数の計算方法がテキストと異なるのかもしれません。

【分析～テキストにならって】
信号検出力（$${\mu_d}$$）の値より、体験に基づく感情の表情を見分けることができたと考えられ、特に95%HDI区間が0より離れているので検出力が大きい、と読めるようです。
また、判断基準と信号検出力の相関はほぼ０なので、信号検出力が大きい実験参加者の判断基準が大きくなる（または小さくなる）といった相関関係はなさそうです。

モデル３：テキストの数式モデルを再現する

テキストの数式モデルを（私のスキルで可能なレベルで）再現してみます。
実験参加者ごとの判断基準$${c_i}$$と信号検出力$${d_i}$$が２変量正規分布に従うモデルです。

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。

$$
\begin{align*}
\mu_c &\sim \text{Uniform}\ (\text{lower}=-5,\ \text{upper}=5) \\
\mu_d &\sim \text{Uniform}\ (\text{lower}=-5,\ \text{upper}=5) \\
mus &= [\mu_c,\ \mu_d] \\
\\
\sigma_c &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=5) \\
\sigma_d &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=5) \\
\rho &\sim \text{Uniform}\ (\text{lower}=-1,\ \text{upper}=1) \\
covs &= [[\sigma_c^2,\ \rho \sigma_c \sigma_d],[\rho \sigma_c \sigma_d,\ \sigma_d^2]]\\
\\
cd &\sim \text{MvNormal}\ (\text{mu=mus,\ \text{cov}=covs}),\ \text{dims}=(id,\ 2) \\
c,\ d &= cd[:, 0],\ cd[:, 1],\ \text{dims}=id \\
\\
\eta &= -c[idIdx] + d[idIdx] \times Display,\ \text{dims}=data \\
p &= \text{invprobit}\ (\eta),\ \text{dims}=data \\
lilekihood &\sim \text{Bernoulli}\ (\text{p}=p) \\
\\
responceBias &= c - d/2,\ \text{dims}=id
\end{align*}
$$

１．モデルの定義

### モデルの定義
with pm.Model() as model_sdt2:
    
    ### データ関連定義
    ## coordの定義
    # データ全体のインデックス
    model_sdt2.add_coord('data', values=data.index, mutable=True)
    # 実験参加者ID
    model_sdt2.add_coord('id', values=sorted(data['obs'].unique()),
                        mutable=True)
    # パラメータc・dの識別
    model_sdt2.add_coord('cdLabel', values=['c', 'd'], mutable=True)
    model_sdt2.add_coord('cdLabel2', values=['c', 'd'], mutable=True)
    
    ## dataの定義
    # 目的変数：映像の表情が体験表情か否かの回答（0:いいえ、1:はい）
    y = pm.ConstantData('y', value=data['eva'], dims='data')
    # 説明変数：映像の表情が意図か体験かの正解値（0:意図表情、1:体験表情）
    Display = pm.ConstantData('Display', value=data['Feel'].values, dims='data')
    # 実験参加者IDのインデックス
    idIdx = pm.ConstantData('idIdx', value=data['obs'].values -1, dims='data')

    ### 事前分布
    ## c:判断基準、d:信号検出力
    # c,dの平均
    muC = pm.Uniform('muC', lower=-5, upper=5)
    muD = pm.Uniform('muD', lower=-5, upper=5)
    mus = pm.Deterministic('mus', pt.stack([muC, muD]), dims='cdLabel')
    # c,dの標準偏差
    sigmaC = pm.Uniform('sigmaC', lower=0, upper=5)
    sigmaD = pm.Uniform('sigmaD', lower=0, upper=5)
    # パラメータc,dの相関係数
    rho = pm.Uniform('rho', lower=-1, upper=1)
    # c,dの分散共分散行列
    covs = pm.Deterministic('covs',
                pt.stacklists([[pt.pow(sigmaC, 2), rho * sigmaC * sigmaD],
                               [rho * sigmaC * sigmaD, pt.pow(sigmaD, 2)]]),
                dims=('cdLabel', 'cdLabel2'))
    # c,dが従う２変量正規分布
    cd = pm.MvNormal('cd', mu=mus, cov=covs, dims=('id', 'cdLabel'))
    # cd行列からcベクトル,dベクトルを分離
    c = pm.Deterministic('c', cd[:, 0], dims='id')
    d = pm.Deterministic('d', cd[:, 1], dims='id')
    
    # η：表情の種類Displayによる傾きと切片の線形結合
    eta = pm.Deterministic('eta', -c[idIdx] + d[idIdx] * Display, dims='data')
    # 確率p：pm.invprobit(η)でηをプロビット変換
    p = pm.Deterministic('p', pm.math.invprobit(eta), dims='data')

    ### 尤度
    likelihood = pm.Bernoulli('likelihood', p=p, observed=y, dims='data')
    
    ### 計算値
    # 反応バイアス：体験なし分布が標準正規分布N(0,1)であると仮定
    resBias = pm.Deterministic('resBias',  c - d/2, dims='id')

【モデル注釈】省略

２．モデルの外観の確認

### モデルの表示
model_sdt2

【実行結果】
注目するパラメータは muC、muD、sigmaC、sigmaD, rho です。

モデルを可視化します。

### モデルの可視化
pm.model_to_graphviz(model_sdt2)

【実行結果】
大きな図になりました。
パラメータを細かく定義したり、決定論的変数（Deterministic）にして事後分布サンプリングデータを残しているからです。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　40秒
with model_sdt2:
    idata_sdt2 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.9, 
                          nuts_sampler='numpyro', random_seed=1234)

【実行結果】省略

### r_hat>1.1の確認
# 設定
idata_in = idata_sdt2    # idata名
threshold = 1.04         # しきい値

# しきい値を超えるR_hatの個数を表示
(az.rhat(idata_in) > threshold).sum()

【実行結果】
このモデルは$${\hat{R} \leq 1.04}$$をクリアしています。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

事後分布の要約統計量とプロットトレースを確認します。

### 推論データの要約統計情報の表示
pm.summary(idata_sdt2, hdi_prob=0.95, round_to=3)

【実行結果】

### トレースプロットの表示
pm.plot_trace(idata_sdt2, compact=True, divergences=False)
plt.tight_layout();

【実行結果】
少々乱れがあります。
実はトレースプロット描画時の設定で「divergences=False」を指定しており、バーコード非表示にしています。
実際には、発散を示すバーコードがかなり表示されています。
ここでは、$${\hat{R}\leq1.1}$$を判断基準にして収束したものとみなします。

判断基準の平均$${\mu_c}$$、信号検出力の平均$${\mu_d}$$、判断基準の標準偏差$${\sigma_c}$$、信号検出力の標準偏差$${\sigma_d}$$、$${c}$$と$${d}$$の相関$${\rho}$$を確認します。
テキストの表12.2の平均・SD・相関に相当します。

### 信号検出理論による結果：要約統計量　※表12.2の平均・SD・相関係数ρに相当
var_names = ['muC', 'muD', 'sigmaC', 'sigmaD', 'rho']
pm.summary(idata_sdt2, hdi_prob=0.95, var_names=var_names, kind='stats',
           round_to=3)

【実行結果】
こちらの事後統計量もテキストの結果と近い感じがします！
相関係数$${\rho}$$はこちらでは正、テキストは負ですが、両者０付近ということでほぼ一致とみなします。

なお、反応バイアスについては、MCMC実行時に実験参加者$${i}$$ごとに計算してみたものの、全体平均等の計算方法が分からなかったので割愛いたします。

PyMC実装「ベータ分布を用いた多項過程ツリーの階層モデル」

Let's enjoy PyMC & Python !

「ベータ分布を用いた多項過程ツリーの階層モデル」に取り組みます。

準備・データ確認

１．データの読み込み
csvファイルをpandasのデータフレームに読み込みます。

### データの読み込み
data2 = pd.read_csv('T1Tai.csv')
print('data2.shape: ', data2.shape)
display(data2.head())

【実行結果】
全30行、つまり実験参加者数です。
反応（回答）の適否ごとに回答数が集計されています。
実験参加者一人あたり合計回答数は16です。

hit：ヒット数
正解値・体験表情に対して体験表情であると回答した数
miss：ミス数
正解値・体験表情に対して体験表情ではないと回答した数
fa：誤警報数
正解値・意図表情に対して体験表情であると回答した数
cr：正棄却数
正解値・意図表情に対して体験表情ではないと回答した数

全16問（16試行）を４つの確率を用いて回数の分布を示す多項分布が合いそうです！

モデルの定義・推論実行

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。

$$
\begin{align*}
\alpha &\sim \text{Gamma} (\text{alpha}=1,\ \text{beta}0.1),\ \text{shape}=2 \\
\beta &\sim \text{Gamma} (\text{alpha}=1,\ \text{beta}0.1),\ \text{shape}=2 \\
\\
r,\ d &\sim \text{Beta}\ (\text{alpha}=\alpha[0],\ \text{beta}=\beta[0]),\ \text{dims}=id \\
g &\sim \text{Beta}\ (\text{alpha}=\alpha[1],\ \text{beta}=\beta[1]),\ \text{dims}=id \\
\\
p_{hit} &= r + (1 - r) \times g,\ \text{dims}=id \\
p_{miss} &= (1 - r) \times (1 - g),\ \text{dims}=id \\
p_{fa} &= (1 - d) \times g,\ \text{dims}=id \\
p_{cr} &= d + (1 - d) \times (1-g),\ \text{dims}=id \\
\theta &= [p_{hit},\ p_{miss},\ p_{fa},\ p_{cr}],\ \text{dims}=id \\
\\
lilekihood &\sim \text{Multinomial}\ (\text{n}=16,\ \text{p}=\theta) \\
\\
\mu &= \alpha / (\alpha + \beta),\ \text{shape}=2 \\
\sigma &= \sqrt{\alpha \beta} / ((\alpha + \beta) \times \sqrt{\alpha + \beta + 1}),\ \text{shape}=2 \\
\end{align*}
$$

１．モデルの定義

### モデルの定義

## 初期値設定：実験参加者１人あたりの問題数（試行数）
n = 16

## モデルの定義
with pm.Model() as model_mpt:
    
    ### データ関連定義
    ## coordの定義
    # データ全体のインデックス
    model_mpt.add_coord('id', values=data2.index, mutable=True)
    # 信号種類 hit, miss, fa, cr
    model_mpt.add_coord('signal', values=['ヒット', 'ミス', '誤警報', '正棄却'],
                        mutable=True)
    # パラメータ種類 r,d,g ※テキストの制約１よりr=d→パラメータは実質rとgの２つ
    model_mpt.add_coord('param', values=['r', 'g'], mutable=True)
    
    ## dataの定義
    # 目的変数：映像の表情が体験表情か否かの回答（0:いいえ、1:はい）
    y = pm.ConstantData('y', value=data2[['hit', 'miss', 'fa', 'cr']].values,
                        dims=('id', 'signal'))

    ### 事前分布
    ## ベータ分布のパラメータα,β ※制約１によりshape=2
    alpha = pm.Gamma('alpha', alpha=1, beta=0.1, dims='param')
    beta = pm.Gamma('beta', alpha=1, beta=0.1, dims='param')
    
    ## 体験弁別パラメータr, 意図弁別パラメータd=r, 憶測パラメータg
    # ※テキストの制約１よりd=r
    r = pm.Beta('r', alpha=alpha[0], beta=beta[0], dims='id')
    d = pm.Deterministic('d', r, dims='id')
    g = pm.Beta('g', alpha=alpha[1], beta=beta[1], dims='id')
    
    ## 信号ごとの確率
    # ヒット率 正解値・体験表情に対して体験表情であると回答する率
    pHit = pm.Deterministic('pHit', r + (1 - r) * g, dims='id')
    # ミス率 正解値・体験表情に対して体験表情ではないと回答する率
    pMiss = pm.Deterministic('pMiss', (1 - r) * (1 - g), dims='id')
    # 誤警報率 正解値・意図表情に対して体験表情であると回答する率
    pFa = pm.Deterministic('pFa', (1 - d) * g, dims='id')
    # 正棄却率 正解値・意図表情に対して体験表情ではないと回答する率
    pCr = pm.Deterministic('pCr', d + (1 - d) * (1 - g), dims='id')
    
    ## 確率行列theta：４つの信号の確率を格納
    theta = pm.Deterministic('theta', pt.stack([pHit, pMiss, pFa, pCr]).T,
                             dims=('id', 'signal'))

    ### 尤度
    likelihood = pm.Multinomial('likelihood', n=n, p=theta, observed=y,
                                dims=('id', 'signal'))
    
    ### 計算値
    # パラメータr, d, gの平均
    mu = pm.Deterministic('mu', alpha / (alpha + beta), dims='param')
    # パラメータr(d), gの標準偏差
    sigma = pm.Deterministic('sigma',
        pt.sqrt(alpha * beta) / ((alpha + beta) * pt.sqrt(alpha + beta + 1)),
        dims='param')

【モデル注釈】省略（テキストの数式モデルに準拠）

２．モデルの外観の確認

### モデルの表示
model_mpt

【実行結果】
注目するパラメータは計算値 mu、sigma です。

モデルを可視化します。

### モデルの可視化
pm.model_to_graphviz(model_mpt)

【実行結果】
大きな図になりました。
パラメータ$${r,d,g}$$がベータ分布に従う点が「ベータ」、尤度が多項分布に従う点が「多項」、パラメータ$${r,d,g}$$を用いた４つの信号の確率$${p_{hit}, p_{miss}, p_{fa}, p_{cr}}$$の計算が「ツリー」、ということなのかな・・・？

３．事後分布からのサンプリング
乱数生成数（draws, tune, chains）はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ1分でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用　1分
# テキスト：iter=20000, burnin=5000, chains=3
with model_mpt:
    idata_mpt = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
                          nuts_sampler='numpyro', random_seed=1234)

【実行結果】省略

### r_hat>1.1の確認
# 設定
idata_in = idata_mpt     # idata名
threshold = 1.02          # しきい値

# しきい値を超えるR_hatの個数を表示
(az.rhat(idata_in) > threshold).sum()

【実行結果】
このモデルは$${\hat{R} \leq 1.02}$$をクリアしています。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

事後分布の要約統計量とプロットトレースを確認します。

### 推論データの要約統計情報の表示
pm.summary(idata_mpt, hdi_prob=0.95, round_to=3)

【実行結果】

### トレースプロットの表示
pm.plot_trace(idata_mpt, compact=True)
plt.tight_layout();

【実行結果】
収束している感じがします。
発散も見られませんでした。

ベータ多項過程ツリーモデルの結果を確認します。
体験弁別パラメータの平均$${\mu_r}$$、推測パラメータの平均$${\mu_g}$$、体験弁別パラメータの標準偏差$${\sigma_r}$$、推測パラメータの標準偏差$${\sigma_g}$$を確認します。
テキストの表12.3に相当します。

### ベータ多項過程ツリーモデルによる結果：要約統計量　※表12.3に相当
var_names = ['mu', 'sigma']
pm.summary(idata_mpt, hdi_prob=0.95, var_names=var_names, kind='stats',
           round_to=3)

【実行結果】
テキストの結果とほぼ一致しました！

【分析～テキストにならって】
体験弁別パラメータの平均$${\mu_r}$$の値より、実験参加者が確信をもって体験から生じた表情を見分けられるのは約４割。
この４割以外で正しく分別できたヒット・正棄却は「推測に基づく可能性が示唆された」とのことのようです。

推論データ（idata）の保存
４つの推論データを再利用する場合に備えてファイルに保存しましょう。
idataをpickleで保存します。

### idataの保存 pickle

file = r'idata_bmb_ch12.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata_bmb, f)

file = r'idata_sdt1_ch12.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata_sdt1, f)

file = r'idata_sdt2_ch12.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata_sdt2, f)

file = r'idata_mpt_ch12.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata_mpt, f)

読み込みコードは次のとおりです。

# ### idataの読み込み pickle

file = r'idata_bmb_ch12.pkl'
with open(file, 'rb') as f:
    idata_bmb_load = pickle.load(f)

file = r'idata_sdt1_ch12.pkl'
with open(file, 'rb') as f:
    idata_sdt1_load = pickle.load(f)

file = r'idata_sdt2_ch12.pkl'
with open(file, 'rb') as f:
    idata_sdt2_load = pickle.load(f)

file = r'idata_mpt_ch12.pkl'
with open(file, 'rb') as f:
    idata_mpt_load = pickle.load(f)

以上で第12章は終了です。

おわりに

対処できないモデル

テキストの全19章のうち、私の能力不足でPyMCモデルを描けなかった第12章もなんとかモデリングできました。
肩の荷が下りる気持ちです。

改めて、PyMCモデル文を書くための条件を振り返ってみました。
テキスト及びソースコード（Rスクリプト・stanスクリプト）の環境が整っていたのだと、再認識しました。

テキストのモデル数式とStanの式がほぼ一致
→処理のイメージがつかめる
テキストのモデル数式の記号とソースコードの変数名がだいたい一致
→データの流れがつかめる
ソースコードの日本語コメントが処理とデータの概要を的確に記述
→RやStanの文法に精通していなくても処理内容をつかめる
　（逆に言うとR・Stan以外のプログラミング言語の解読は困難）

そしてなによりも大切なのは「文章読解力」なのだと痛感しています。
ここでの文章読解力は、テキスト全体を包む「著者独自表現の論理構造」を掴み、「ベイズモデリングの動機・目的・モデル構造」を抽出することです。
テキストを丁寧に隅から隅まで読みほぐせば、何かしらのヒントを得られるはずだ、きっかけが伝わってくるはずだ、と信じること（ベイズの信念）。
そして「たのしいベイズモデリング」シリーズは正式な論文ではなく、学術的コラムなので、なんとか読みほぐせるはずだと安心感をもち、匍匐前進でもいいから理解に務めようとする頑張り、といったものも必要そうです。
モデルを理解できてはじめてPyMC翻訳に進めます。

シリーズの記事

次の記事

前の記事

ブログの紹介

note で４つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。

２．RとStanではじめる心理学のための時系列分析入門を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ（お題）を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます！
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀

３．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。

４．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。

最後までお読みいただきまして、ありがとうございました。

この記事が気に入ったらサポートをしてみませんか？