第13章「消極的な発言は他のメンバーの生産性を低下させるか」のベイズモデリングをPyMC Ver.5 で

2023年12月23日 11:43

この記事は、テキスト「たのしいベイズモデリング」の第13章「集団メンバーの消極的な発言は他メンバーのパフォーマンスを低下させるか」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。

この章では、集団作業中にメンバーの一人が「つまらない作業だ」等の消極的な発言をしたとき、集団作業のパフォーマンスが低下するかどうかを調べています。

今回はテキストに近い推論結果を得ることができました！
~~前回は「棄権」して悔しい思いをしたので、今回の結果はとても嬉しいです（泣）~~

果たして消極的発言でメンバーのモチベーションは下がるのでしょうか？
PyMCでモデリングして、ベイズを楽しみましょう！

テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。

テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。

サマリー

テキストの概要

執筆者　　　：　後藤崇志先生
モデル難易度：　★★・・・　（やさしめ）

自己評価

評点

$$
\begin{array}{c:c:c}
実装精度 & ★★★★★& GoooD!! \\
結果再現度 & ★★★★★& 最高✨ \\
楽しさ & ★★★★★& 楽しい！ \\
\end{array}
$$

評価ポイント

実はこの記事の書き出し当初は、勝手モデルの推論結果がテキストとかなり乖離していました。
粘り強くモデルの見直しを行ったことで、最終的にテキストに近い結果に結ぶことができました。

工夫・喜び・反省

テキストのモデル数式の切片・傾きの単位が「全体単位」「グループ単位」「個人単位」のいずれに該当するかうまく読み取れず、Stanのモデル記述を咀嚼して、単位を理解しました。
RとStanコードの読み取り能力は低いのですが、今後は、低いなりに丁寧にコードの理解に努めたいと思いました。

モデルの概要

テキストの調査・実験の概要

■手抜きの同調
メンバーの責任が見えにくい集団作業において、消極的な発言をするメンバーに影響されて、他のメンバーがやる気を低下させ、集団的な手抜きにつながるかどうかを実験して、データを取得します。
取得データについて、「グループ（集団）レベル」－「個人レベル」の階層を想定したベイズモデリングを用いて、２つの問いの分析を行います。

■実験前の計画と実験手続き
テキストでは、仮説を設定して分析計画を立案し、さらに実験当日の不測の事態発生（参加者が来ないなど）に対応すべく分析計画を修正する、といった実験の生々しいリアルが記載されています。
実験の内容は図を用いて丁寧に説明しています。
とても参考になります！

テキストのモデリング

■目的変数と関心のあるパラメータ
目的変数$${post_i}$$は後半の作業量です。
最も関心のあるパラメータは、実験操作（消極的な発言の有無）の係数である$${\gamma_{03}}$$です。

■モデル
１行目の数式は「個人レベル」を示しています。
２行目の$${b_0}$$：個人レベルの切片、３行目の$${b_1}$$：個人レベルの傾きは、「集団レベル」を示しています。
添字$${i}$$は参加者の識別番号、$${g[i]}$$は参加者$${i}$$が所属する集団$${g}$$の識別番号です。

$$
\begin{align*}
\mu_i &= b_0 + b_1 \times pre(gc)_i \\
b_0 &= \gamma_{00} + \gamma_{01} \times pre(gm)_{g[i]} + \gamma_{02} \times peerN_{g[i]} + \gamma_{03} \times cond_{g[i]} \\
b_1 &= \gamma_{10}
\end{align*}
$$

テキストより引用

以下は上記の式を統合して実装につなげるモデルです。

$$
\begin{align*}
post_i &\sim \text{Normal}\ (\mu_i,\ \sigma) \\
\mu_i &= \gamma_{00} + \gamma_{10} \times pre(gc)_i + \gamma_{01} \times pre(gm)_{g[i]} + \gamma_{02} \times peerN_{g[i]} + \gamma_{03} \times cond_{g[i]}\\
\gamma_{00} &\sim \text{Normal}\ (\mu_{\gamma_{00}},\ \tau_{00}) \\
\gamma_{10} &\sim \text{Normal}\ (\mu_{\gamma_{10}},\ \tau_{10}) \\
\gamma_{01}, \gamma_{02}, \gamma_{03} &\sim \text{Normal}\ (0,\ 100) \\
\tau_{00}, \tau_{10}, \sigma &\sim \text{Cauchy}\ (0,\ 100)
\end{align*}
$$

テキスト・Rスクリプトより引用

【変数の内容】
$${post_i}$$：参加者$${i}$$の後半の作業量
$${\mu_i}$$：参加者$${i}$$の後半の作業量の平均値
$${\sigma}$$：後半の作業の標準偏差
$${pre(gc)_i}$$：参加者$${i}$$の前半の作業量－当該参加者が所属する集団の前半の作業量（個人レベルの前半の作業量）
$${pre(gm)_{g[i]}}$$：集団ごとの前半の作業量の平均値（集団レベルの前半の作業量）
$${peerN_{g[i]}}$$：集団の人数
$${cond_{g[i]}}$$：実験操作の有無
$${\gamma_{00}}$$：切片（注）
$${\gamma_{10}}$$：個人レベルの前半の作業量の係数（注）
$${\gamma_{01}}$$：集団レベルの前半の作業量の係数
$${\gamma_{02}}$$：集団の人数の係数
$${\gamma_{03}}$$：実験操作の係数
$${\tau_{00}}$$：$${\gamma_{00}}$$の標準偏差
$${\tau_{10}}$$：$${\gamma_{10}}$$の標準偏差

（注）Stanの実装上、$${\gamma_{00},\ \gamma_{10}}$$は集団レベルの変数です。

■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCモデリングでの分析結果は、「PyMC実装」章の【５．分析】の部分をご覧ください。

PyMC実装

Let's enjoy PyMC & Python !

準備・データ確認

１．インポート

### インポート

# ユーティリティ
import pickle

# 数値・確率計算
import pandas as pd
import numpy as np

# PyMC
import pymc as pm
import arviz as az

# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

２．データの読み込みと前処理
csvファイルをpandasのデータフレームに読み込みます。

### データの読み込み

# データの読み込み
data_orgn = pd.read_csv('loafing_data.csv')

# データの表示
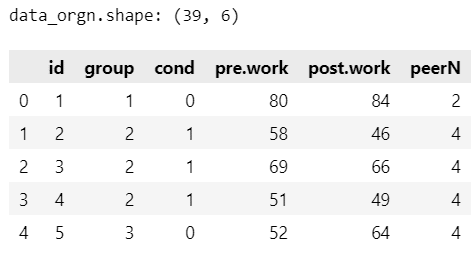
print('data_orgn.shape:', data_orgn.shape)
display(data_orgn.head())

【実行結果】
全３９行、６列です。
データ項目は次のとおりです。
id：参加者の識別番号（全39名）
group：集団の識別番号（全17グループ）
cond：消極的な発言の有無（0：発言なし・統制、1：発言あり・実験）
pre.work：前半の作業量
post.work：後半の作業量（目的変数）
peerN：集団の人数

３．データの外観・統計量

ひとまず要約統計量を確認します。

### 要約統計量の表示
data_orgn.describe().round(2)

【実行結果】
全体的には「後半の作業量の方が大きい」ようです。
作業の習熟度があがったり、前半よりも多く作ろうとするモチベーションが上がったのでしょうか？

テキストにならって箱ひげ図を描画します。
matplotlibのboxplotを利用します。
テキストの図13.2に相当します。

### 条件ごとの作業量の箱ひげ図の描画 ★図13.2に相当

fig, ax = plt.subplots(figsize=(6, 3))
# 箱ひげ図の描画
ax.boxplot([data_orgn[data_orgn['cond']==0]['pre.work'],
            data_orgn[data_orgn['cond']==1]['pre.work'],
            data_orgn[data_orgn['cond']==0]['post.work'],
            data_orgn[data_orgn['cond']==1]['post.work']])
# 修飾
ax.set(xticklabels=['前半－統制群', '前半－実験群', '後半－統制群', '後半－実験群'],
       ylabel='作業量')
plt.show()

【実行結果】
消極的な発言がある実験群は前半も後半もバラツキ加減が大きい感じがします。
後半作業を見ると、消極的な発言がある実験群のほうが平均作業量が小さいようです。

データの前処理を実施します。
集団ごとの前半作業量（所属する個人の作業量の平均値）を算出します。
また、前半作業量と集団の人数の値を中心化（平均値を差し引く）します。

### データの前処理

# 集団ごとの前半作業量の平均preGmeanの算出
tmp = (data_orgn.groupby(['group'])[['pre.work']].mean().reset_index()
       .rename(columns={'pre.work': 'preGmean'}))
data = pd.merge(data_orgn, tmp, on='group', how='left')

# pre.workの集団中心化
data['pre.work'] = data['pre.work'] - data['preGmean']

# peerNの全体中心化
data['peerN'] = data['peerN'] - data['peerN'].mean()

# preGmeanの全体中心化
data['preGmean'] = data['preGmean'] - data['preGmean'].mean()

# 加工後のデータの表示
print('data.shape:', data.shape)
display(data.head())

【実行結果】

モデル構築

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$${\gamma_{00}}$$と$${\gamma_{10}}$$の単位は「group単位」です。

$$
\begin{align*}
\gamma_{01}, \gamma_{02}, \gamma_{03}, \mu_{\gamma_{00}}, \mu_{\gamma_{10}} &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=100)\\
\tau_{00}, \tau_{00} &\sim \text{HalfCauchy}\ (\text{beta}=100)\\
\gamma_{00}[group] &\sim \text{Normal}\ (\text{mu}=\mu_{\gamma_{00}},\ \text{sigma}=\tau_{00}) \\
\gamma_{10}[group] &\sim \text{Normal}\ (\text{mu}=\mu_{\gamma_{10}},\ \text{sigma}=\tau_{10}) \\
\mu &= \gamma_{00}[group] + \gamma_{10}[group] \times pre(gc) + \gamma_{01} \times pre(gm) + \gamma_{02} \times peerN + \gamma_{03} \times cond\\
\sigma &\sim \text{HalfCaushy}\ (\text{beta}=100) \\
likelihood &\sim \text{Normal}\ (\text{mu}=\mu,\ \text{sigma}=\sigma) \\
\end{align*}
$$

１．モデルの定義
初期値設定でgroupの値を-1してインデックス化しています。
$${\gamma_{00}, \gamma_{10}}$$のインデックスに用います。
またこのモデルは説明変数が多いので、「data」の定義数も多くなっています。

### モデルの定義

# 初期値設定：集団groupの番号とインデックスを作成
group_cat = sorted(data['group'].unique())  # 集団の番号を1から昇順で取得
group_idx = list(data['group'].values - 1)  # 列group値を0始まりに変更

with pm.Model() as model:
    
   ### データ関連定義
   ## coordの定義
   model.add_coord('id', values=data['id'].values, mutable=True)
   model.add_coord('group', values=group_cat, mutable=True)
   
   ## dataの定義
   # 目的変数：個人レベルの後半の作業量post.work
   y = pm.ConstantData('y', value=data['post.work'], dims='id')
   # 個人が所属する集団groupのインデックス
   groupIdx = pm.ConstantData('groupIdx', value=group_idx, dims='id')
   # 個人レベルの前半の作業量pre.work_c
   preGc = pm.ConstantData('preGc', value=data['pre.work'], dims='id')
   # 集団レベルの前半の作業量pre.work_m_gm
   preGm = pm.ConstantData('preGm', value=data['preGmean'], dims='id')
   # 集団の人数peerN_g
   peerN = pm.ConstantData('peerN', value=data['peerN'], dims='id')
   # 実験操作の有無(0:統制、１：実験)cond
   cond = pm.ConstantData('cond', value=data['cond'], dims='id')
   
   ### 事前分布
   # 集団レベルの前半の作業量の係数
   gamma01 = pm.Normal('gamma01', mu=0, sigma=100)
   # 集団の人数の係数
   gamma02 = pm.Normal('gamma02', mu=0, sigma=100)
   # 実験操作（発言の有無）の係数
   gamma03 = pm.Normal('gamma03', mu=0, sigma=100)
   # 切片γ00のmu
   muGamma00 = pm.Normal('muGamma00', mu=0, sigma=100)
   # 個人レベルの前半の作業量γ10のmu
   muGamma10 = pm.Normal('muGamma10', mu=0, sigma=100)
   # 切片γ00の標準偏差
   tau00 = pm.HalfCauchy('tau00', beta=100)
   # 個人レベルの前半の作業量の係数γ10の標準偏差
   tau10 = pm.HalfCauchy('tau10', beta=100)
   # 切片
   gamma00 = pm.Normal('gamma00', mu=muGamma00, sigma=tau00, dims='group')
   # 個人レベルの前半の作業量の係数
   gamma10 = pm.Normal('gamma10', mu=muGamma10, sigma=tau10, dims='group')
   # 後半の作業量の標準偏差
   sigma = pm.HalfCauchy('sigma', beta=100)
   
   ### 後半の作業量の期待値muの計算
   mu = pm.Deterministic('mu',
      (gamma00[groupIdx] + gamma10[groupIdx] * preGc + gamma01 * preGm
       + gamma02 * peerN + gamma03 * cond),
      dims='id')
   
   ### 尤度
   likelihood = pm.Normal('likelihood', mu=mu, sigma=sigma, observed=y, 
                          dims='id')
   
   ### 計算値
   # 効果量
   es = pm.Deterministic('es', gamma03 / sigma)
   # 切片の平均値に対する平均値差の割合
   rate = pm.Deterministic('rate', gamma03 / muGamma00)

【モデル注釈】

coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の２つを設定しました。
・行の座標：名前「data」、値「行インデックス」
・集団の座標：名前「group」、値「1～17の整数」
dataの定義
目的変数$${y}$$、集団のインデックス$${groupIdx}$$、説明変数を４つ設定しました。
パラメータの事前分布
説明変数の係数等は正規分布、標準偏差は半コーシー分布を仮定しています。
muの計算
モデルに定義した後半の作業量の期待値muの計算のとおりです。
尤度
muとsigmaをパラメータにする正規分布に従います。
計算値
テキストの「13.6 結果」で利用する「効果量」と「割合」を計算します。

２．モデルの外観の確認

### モデルの表示
model

【実行結果】
Stanコードでは変数内に複数のベクトルを配置しているので変数の数が少ないです。
一方でこちらのモデルではテキストの数式の変数や推論結果を示す変数になるべく寄り添おうと考えて、変数の数が多いです。

### モデルの可視化
pm.model_to_graphviz(model)

【実行結果】
「mu」をハブにしてさまざまな確率変数、説明変数がギュッと集まっています。

３．事後分布からのサンプリング
乱数生成数（draws, tune）はテキストと同様です。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ３分３０秒でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを未使用　3分30秒
with model:
    idata = pm.sample(draws=200000, tune=200000, chains=4, target_accept=0.95,
                      nuts_sampler='numpyro', random_seed=1234)

【実行結果】省略

４．サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R}\leq 1.1}$$としています。

### r_hat>1.1の確認
rhat_idata = az.rhat(idata)
(rhat_idata > 1.1).sum()

【実行結果】
$${\hat{R} >1.1}$$のパラメータは「０」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

推論データの要約統計量です。

### 推論データの要約統計量
pm.summary(idata, hdi_prob=0.95)

【実行結果】
推論対象の変数が多いため、途中省略されました（汗）

トレースプロットです。

### トレースプロットの描画
pm.plot_trace(idata, var_names=var_names, combined=True, compact=False,
              figsize=(15, 20))
plt.tight_layout();

【実行結果】
発散を示すバーコードが結構出ています。。。
左側の分布の様子では、突起のような異様な密度の高い部分が見られます。。。

５．分析
テキストの表13.1に相当する主要変数の要約統計量を確認します。

### 推論データの要約統計量の表示 ★表13.1に対応
var_names = ['muGamma00', 'muGamma10', 'gamma01', 'gamma02', 'gamma03',
             'tau00', 'tau10', 'sigma', 'es', 'rate']
pm.summary(idata, hdi_prob=0.95, var_names=var_names)

【実行結果】
平均（mean、テキストのEAP）や標準偏差（sd、テキストのpost.sd）はテキストに近い値になりました（ホッ）。

【分析】

①「消極的な発言」がある場合の作業量が発言のない場合よりも低くなる確率

$${\gamma_{03}}$$の推定値は$${-2.982}$$（95%HDI＝[-9.079, 3.139]）です。
平均的には、消極的な発言は負の影響を及ぼすということでしょう。
$${\gamma_{03}}$$が0未満となる確率を計算します。

### γ03が0より小さい確率の計算
gamma03_sample = idata.posterior.gamma03.data.flatten()
print('P(γ03<0)=', (gamma03_sample < 0).sum() / gamma03_sample.size)

【実行結果】

０未満になる確率は$${85\%}$$です。
消極的な発言がある場合の作業量の平均が消極的な発言がない場合よりも低くなる確率が$${85\%}$$という結果です。

②「消極的な発言」がある場合の作業量の平均の減少

効果量（es）の推定値は$${-0.495}$$（95%HDI＝[-1.552, 0.523]）です。
消極的な発言がある場合の作業量の平均が消極的な発言がない場合よりも標準偏差の$${49.5\%}$$小さくなるという結果です。
また、割合（rate）の推定値は$${-0.048}$$（95%HDI＝[-0.145, 0.051]）です。
消極的な発言がある場合の作業量の平均が消極的な発言がない場合よりも$${4.8\%}$$小さくなるという結果です。
ただし、効果量も割合も、95%HDIの範囲に０以上を含んでいるので、「小さくなる」ことの解釈に際しては注意が必要です。

６．推論データ（idata）の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idataをpickleで保存します。

### idataの保存 pickle
file = r'idata_ch13.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata_ch13.pkl'
with open(file, 'rb') as f:
    idata_load = pickle.load(f)

以上で第13章は終了です。

おわりに

PyMCモデル化の困難と限界突破

第13章までのモデルのうち、テキスト初見時に「PyMC化は無理そうだ」と及び腰になった章が８つありました。
６割程度の章を棄権する可能性があったのです。

この第13章も「無理そう」な章でした。
モデルの数式がたくさん並んでいて、パッと見で「複雑」と思い込んだのです。
しかし、各章を実践することが修行となり、モデル化のクリアを繰り返すことが訓練となり、第13章を無事にPyMC化できました（乗り越えました）。

シリーズの記事

次の記事

前の記事

ブログの紹介

note で４つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。

２．RとStanではじめる心理学のための時系列分析入門を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ（お題）を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます！
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀

３．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。

４．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。

最後までお読みいただきまして、ありがとうございました。

この記事が気に入ったらサポートをしてみませんか？