
第1章「2要因配置のAR法」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング」の第1章「大学生は18禁映像をどれくらい見ているか」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
AR法をPyMCでチャレンジして、ベイズ推論を楽しみましょう!
ちなみに私はベイズ推論もPyMCも始めて数ヶ月の初学者です。
Rは不慣れ、Stanは動かしたことがありません。
ですので、皆さんのお知恵をお借りして一緒に、たのしいPyMCベイズモデリングをできたなら、とても嬉しいです!

テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 豊田秀樹 先生
モデル難易度: ★★★★★ (難しい)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★・・& そこそこ\\
結果再現度 & ★★・・・& やや悪い\\
楽しさ & ★★★★★ & 楽しい! \\
\end{array}
$$

評価ポイント
第1章から「ラスボス級」の難しいモデルに出会って四苦八苦しました!
目的変数$${y}$$の値によって変動する「マスク$${\boldsymbol{m}_k^{\prime}}$$」を利用した混合分布の実装が難しかったです。
2要因配置を正しくモデリングできたか不安があり、事後分布の要約統計量の不一致が気になっています。

工夫・喜び・反省
次の2点の実装に取り組んだことで、PyMCの理解度が深まりました!
modelのcoordとdataを使ったこと
次元に気をつけられるようになり、また、データ閲覧時にカテゴリ値が分かりやすくなりました。混合分布Mixture、カスタム分布CustomDistの利用と、確率分布の.dist()を関数で生成したこと
使える分布の範囲がグンと広がった気分です!
モデルの概要
テキストの調査・実験の概要
下図をご覧ください。
AR法による間接質問で得られた回答「視聴日数±誕生月」が目的変数$${y}$$になります。
ベイズモデリングで「月当たりの視聴日数」を推論します。

センシティブな情報を収集するということで、テキストによると調査開始前に、次のようなことを質問者から回答者へ、丁寧に説明したそうです。
十分プライバシーを守る約束をすること
質問者(調査側)が個人を特定しないこと
誰にも見られないようにコイントスすることでプライバシーが守られること
回答したくない場合は、回答しなくてよいこと
指示に従って正しく回答することで、適切な分析ができるようになること
調査結果を回答者全員に報告すること
テキストのモデリング
$${y}$$は回答(目的変数)、$${x}$$は真の視聴日数、$${\mu_{days}}$$は$${x}$$の平均です。
■マスク$${m_k^{'}}$$を用いた混合分布
このモデルの鍵を握るのは「マスク$${m_k^{'}}$$」です!
マスクは、コインの表裏によって視聴日数に加減算する「プラスマイナス付きの誕生月」のことです。最小値は$${-12}$$、最大値は$${+12}$$です。
$$
f(y \mid \mu_{days}, \sigma_e) = \sum_{k \subset A} \cfrac{1}{N(k \subset A)} f(y-m_k^{\prime} \mid \mu_{days}, \sigma_e) \\
$$
$${f(\ \mid \mu_{days}, \sigma_e)}$$は、$${\mu_{days}}$$を平均、$${\sigma_e}$$を標準偏差とする正規分布の確率密度関数です。
■マスク$${m_k^{'}}$$、集合$${A}$$、関数$${N(k \subset A)}$$
マスク$${\boldsymbol{m_k^{'}}}$$の取りうる値の集合$${\boldsymbol{A}}$$は回答$${\boldsymbol{y}}$$の値によって変動します。
たとえば回答$${y=2}$$の場合、加減算する誕生月(=マスク)は、コイン裏&12月の$${-12}$$から、コイン表&2月の$${+2}$$までが取りうる値になります。
コイン表&3月を考えると、視聴日数の最小値が$${0}$$のため回答は$${3}$$以上になってしまい、回答$${y=2}$$に収まらなくなるので、マスクの値は$${+3}$$以上にならないのです。
まとめますと、回答$${y=2}$$の場合、マスクの値の集合$${A=\{ -12, -11, \cdots, -1, 1, 2\}}$$となり、要素数$${N(k \subset A)}$$は$${14}$$となります。
回答$${y}$$とマスクの関係を表にしました。

■混合分布であること
$${f(y-m_k^{\prime} \mid \quad)}$$は、$${y}$$の値によって変動する集合$${A}$$の要素の数(=マスクの数)だけ、確率分布が存在することを示しています。
回答$${\boldsymbol{y}}$$の値によって、混合する「確率分布の数が変動する」のです!
たとえば$${y=2}$$の場合、混合分布は、以下の$${14}$$個の確率密度関数を$${1/14}$$づつ均等に混合したものになります。
$$
f(y+12 \mid \mu, \sigma_e) \\
f(y+11 \mid \mu, \sigma_e) \\
\vdots \quad (中略※) \\
f(y+1 \mid \mu, \sigma_e) \\
f(y-1 \mid \mu, \sigma_e) \\
f(y-2 \mid \mu, \sigma_e) \\
$$
※途中の9つの確率密度関数を記載省略
■2要因配置
$${\mu_{days}}$$を次の2要因配置の実験計画モデルで表現しています。
$$
\mu_{days} = \mu + a_j + b_{j^{'}} + (ab)_{jj^{'}}, \quad (j=1, 2, \ j^{'}=1, 2) \\
$$
$${a_j}$$は要因A「性別」の水準の効果、$${b_{j^{'}}}$$は要因B「恋人の有無」の水準の効果です。
$${(ab)_{jj^{'}}}$$は要因Aと要因Bの交互作用項です。
性別は$${j=1}$$が女性、$${j=2}$$が男性です。
恋人の有無は$${j^{'}=1}$$がいない、$${j^{'}=2}$$がいるです。
■パラメータの事前分布
パラメータ$${\mu, a_j, b_{j^{'}}, (ab)_{jj^{'}}, \sigma_e}$$は十分に範囲の広い一様分布を利用することとしています。
■分析結果
テキストに記載のとおりです。
PyMCモデリングでの分析結果は、「PyMC実装」章の<分析結果を早く見たい方はここから>の部分をご覧ください。
PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import os
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
# numpyro/jaxのCPUコア利用数の指定
os.environ['XLA_FLAGS'] = '--xla_force_host_platform_device_count=4'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込み・前処理
データ項目と値は、AV:回答、sex:性別(0:女性、1:男性)、lover:恋人の有無(0:いない、1:いる)です。
Rスクリプトに記載の異常値削除を施しています。
### データの読み込み
# 項目 sex 0:女性, 1:男性、 lover 恋人が 0:いない、1:いる
data = pd.read_csv(r'楓.csv')
# 異常値の削除:理論的な上限43を超える異常値を削除
data = data[data['AV']<=43].reset_index(drop=True)
display(data)【実行結果】

3.データの外観・統計量(テキストの表1.1~1.2、図1.1に対応)
pandasのcrosstabを利用してクロス集計表を作成します。
### 性別・恋人有無のクロス集計表 ★表1.1に対応
# 集計用データdata2の作成
data2 = data.copy()
data2['sex'] = data['sex'].apply(lambda x: np.where(x==0, '女性', '男性'))
data2['lover'] = data['lover'].apply(lambda x: np.where(x==0, 'いない', 'いる'))
data2.columns = ['回答', '性別', '恋人']
# クロス集計表の表示
pd.crosstab(index=data2['性別'], columns=data2['恋人'], margins=True,
margins_name='全体')【実行結果】
回答者の性別と恋人の有無に偏りがあることが確認できました。
女性の割合が高く、恋人のいない人の割合が高いです。
また、恋人のいる割合は女性のほうが高いようです。

matplotlibで回答のヒストグラムを描画します。
### 回答のヒストグラム ★図1.1に対応
plt.hist(data2['回答'], bins=12);【実行結果】

pandasのboxplotを利用して箱ひげ図を描画します。
### 性別・恋人有無の組み合わせごとの回答の箱ひげ図 ★図1.1に対応
ax = data2.boxplot(column='回答', by=['性別', '恋人'])
ax.axhline(0, color='black', lw=0.5, ls='--')
plt.tight_layout();【実行結果】
男性の方が回答の値が大きめに見えます。
また、外れ値が男性にだけ見られるのが面白いです。

pandasで回答の平均値を作成・表示します。
### 回答の平均値 ★表1.2に対応
display(data2[['回答']].mean().to_frame(name='全体').round(1))
display(data2.groupby(['性別'])[['回答']].mean().T.round(1))
display(data2.groupby(['恋人'])[['回答']].mean().T.round(1))
display(data2.groupby(['性別', '恋人'])[['回答']].mean().T.round(1))【実行結果】
各カテゴリの回答(マスク済み)の平均値がベイズモデリングで推論する視聴回数の平均値とどのように相違するか、楽しみです!


モデル3でMCMC
PyMCモデリング その1「モデル3」
いよいよモデリングです!
いくつかのモデルを試行錯誤で作成しましたが、ブログではモデル3とモデル4を紹介いたします。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$$
\begin{align*}
\mu &\sim \text{Uniform}(-100, 100) \\
a &\sim \text{Uniform}(-100, 100) \\
b &\sim \text{Uniform}(-100, 100) \\
ab &\sim \text{Uniform}(-100, 100) \\
\sigma_e &\sim \text{Uniform}(0, 100) \\
\mu_{days} &= \mu + a \cdot data.sex + b \cdot data.lover + ab \cdot data.sex \cdot data.lover \\
components &= [ \\
&\text{Normal.dist}(\text{mu} =\mu_{days}, \ \text{sigma}=\sigma_e) -12, \\
&\text{Normal.dist}(\text{mu} =\mu_{days}, \ \text{sigma}=\sigma_e) -11, \\
&\quad \vdots \\
&\text{Normal.dist}(\text{mu} =\mu_{days}, \ \text{sigma}=\sigma_e) -1, \\
&\text{Normal.dist}(\text{mu} =\mu_{days}, \ \text{sigma}=\sigma_e) +1, \\
&\quad \vdots \\
&\text{Normal.dist}(\text{mu} =\mu_{days}, \ \text{sigma}=\sigma_e) +11, \\
&\text{Normal.dist}(\text{mu} =\mu_{days}, \ \text{sigma}=\sigma_e) +12 \\
] \\
likelihood &\sim \text{Mixture}(\text{comp\_dist}=components, \ \text{weight}=w) \\
\end{align*}
$$
1.初期値設定
混合分布のウエイト(重み)$${w}$$を算出します。
回答$${y}$$の値に応じてマスクの数$${N}$$を求めます。
混合分布に用いる確率分布が24本あるので、重み$${w}$$の配列は1行あたり24の要素で構成しています。
混合分布の確率分布と重みは、次の図のような関係をイメージしています。

for文で配列の先頭から$${N}$$個までに$${1/N}$$をセットします。
残りの要素は$${0}$$とし、重み0の混合分布が使われないようにします。
### 初期値設定
## データのインデックス、カテゴリ変数のインデックスの取得
idx_data = data.index
## 混合分布の混合割合w:観測データ(全122行)ごとにマスク個数分の均等割合を算出
# wの初期化
w = np.zeros((len(data), 24))
# 観測値AVごとに可能なマスク個数を算出(テキストのN()関数が返すAの要素数に相当)
Ns = data['AV'].apply(lambda x: x + 13 if x<=-1 else x + 12 if x<=12 else 24)
# w(numpy配列)の作成
for i, N in enumerate(Ns):
# 配列先頭からマスクの個数までの要素を1/Nにする
w[i, :N] = 1 / N
# wの表示
print('混合割合w: shape=', w.shape)
print(w)【実行結果】
重み配列$${w}$$の一部を表示しました。

2.モデルの定義
3つ告白します。
1つ目はカスタム分布関数の定義に対する不安です。
テキストのモデル「$${f(y-m_k^{\prime} \mid \mu_{days}, \sigma_e)}$$」を「$${f(y \mid \mu_{days}, \sigma_e) + m_k^{\prime}}$$」に書き換えています。
この書き換えが正しいかどうか、とても不安です。
2つ目は月平均視聴日数muDaysの計算に対する不安です。
2要因配置の実験計画モデルを重回帰のように「$${切片 + 係数 \times 説明変数}$$」と記述しています。
モデルを正しく書けているか、とても不安です。
3つ目は事後分布の要約統計量はテキストとかなり相違しています。
有識者のみなさま「ぜひアドバイスをお願いします!」
### モデルの定義
# カスタム分布関数の定義:正規分布+マスクm ★この正規分布の設定に自信なし
def custom_dist(
mu: pt.TensorVariable,
sigma: pt.TensorVariable,
m: pt.TensorVariable,
size: pt.TensorVariable,
) -> pt.TensorVariable:
return pm.Normal.dist(mu=mu, sigma=sigma, size=size) + m # '+m'に注目
# モデルの定義
with pm.Model() as model3:
### データ関連定義
# coordの定義
model3.add_coord('data', values=data.index, mutable=True)
model3.add_coord('sex', values=['女性', '男性'], mutable=True)
model3.add_coord('lover', values=['いない', 'いる'], mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data['AV'].values, dims='data')
xSex = pm.ConstantData('xSex', value=data['sex'].values, dims='data')
xLover = pm.ConstantData('xLover', value=data['lover'].values, dims='data')
### 事前分布
mu = pm.Uniform('mu', lower=-100, upper=100)
a = pm.Uniform('a', lower=-100, upper=100)
b = pm.Uniform('b', lower=-100, upper=100)
ab = pm.Uniform('ab', lower=-100, upper=100)
sigmaE = pm.Uniform('sigmaE', lower=0, upper=100)
### 月平均視聴日数muDaysの計算 ★2要因配置の実験計画モデルに合致するか自信なし
muDays = pm.Deterministic('muDays',
mu + a * xSex + b * xLover + ab * xSex * xLover,
dims='data')
### 混合分布に含める確率分布の構成の定義
# マスクのfull集合A {-12, -11, …, -1, 1, …, 12}
A_full = np.delete(np.arange(-12, 13), 12)
# リスト内包表記で24個(マスク個数分)のカスタム正規分布を生成
components = [
pm.CustomDist.dist(muDays, sigmaE, m, dist=custom_dist) for m in A_full
]
### 尤度の計算:混合分布
likelihood = pm.Mixture('likelihood', w=w[idx_data], comp_dists=components,
observed=y, dims='data')【モデル注釈】
パラメータの事前分布である一様分布の範囲は、$${-100~100}$$にしました($${\sigma_e}$$は$${0~100}$$)。
混合分布は次のように実装しました。
尤度likelihoodで 混合分布「pm.Mixture」を指定。混合分布の構成は「components」を参照。各分布の重み(混合割合)はwで指定。
componentsのリストでは「正規分布+$${m_k^{\prime}}$$」を実装するカスタム分布関数「custom_dist」を参照して、リスト内包表記で24個のカスタム分布の確率分布「pm.Custom.dist()」を生成。
カスタム分布関数「custom_dist」では確率分布「正規分布+$${m_k^{\prime}}$$」を生成。
3.モデルの外観の確認
# モデルの表示
model3【実行結果】
likelihoodの確率分布は途中で見切れています。
CustomSymbolicDist(f(), muDays, sigmaE, 12)まで続いています。

# モデルの可視化
pm.model_to_graphviz(model3)【実行結果】
modelのdataを指定したので、目的変数$${y}$$、説明変数$${X_{性別}, X_{恋人}}$$がグレーの角丸四角で表示されています。
また、coordの設定とdimsの指定により、大きな角丸四角内の各変数が、観測データのcoord「data」(データ数122)であることが明示的になりました。

4.事後分布からのサンプリング
乱数生成数はテキストのdraws=50000, tune=1000, chains=20と比べて、減らしています。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間は4分弱でした。
### 事後分布からのサンプリング(サイズを縮小しています) 4分
with model3:
idata3 = pm.sample(draws=100000, tune=50000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
5.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1が0件であることを確認
rhat_idata3 = az.rhat(idata3)
(rhat_idata3>1.1).sum()【実行結果】
$${\hat{R} > 1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

事後分布の要約統計量です。
# 推論データの要約統計量の表示 ★表1.3に対応(MAP・MEDを除く)
var_names = ['mu', 'a', 'b', 'ab', 'sigmaE']
pm.summary(idata3, hdi_prob=0.95, var_names=var_names)【実行結果】
テキスト(表1.3)のEAP(平均)、post.sd(標準偏差)と全然違います(泣)

トレースプロットです。
# トレースプロットの描画
pm.plot_trace(idata3, var_names=var_names, combined=True, figsize=(15, 20))
plt.tight_layout();【実行結果】
テキストとの相違はさておき、きれいなトレースプロットから、収束している感触を満喫しました。

6.テキストの図表(図1.2、表1.5)
まずは図1.2もどきです。
### パラメータaのヒストグラム 図1.2に対応
# パラメータa(水準:男性)の事後分布からのサンプリングデータの取得
a_post = idata3.posterior.a.data.flatten()
# a>0の確率の計算
a_prob = (a_post>0).mean()
# ヒストグラムの描画
plt.hist(a_post, bins=30)
plt.title(f'要因:性別・水準:男性の効果, a>0の確率{a_prob:.1%}')
plt.show()【実行結果】
テキストの図左側と比べて平均(およそ7.5)が右側に寄っている感じがします。

### パラメータbのヒストグラム 図1.2に対応
# パラメータb(水準:いる)の事後分布からのサンプリングデータの取得
b_post = idata3.posterior.b.data.flatten()
# b>0の確率の計算
b_prob = (b_post>0).mean()
# ヒストグラムの描画
plt.hist(b_post, bins=30)
plt.title(f'要因:恋人・水準:いるの効果, b>0の確率{b_prob:.1%}')
plt.show()【実行結果】
こちらはテキストの図左側と比べて、平均の位置は似ていますが、裾が広い(テキストは$${-4~4}$$くらい)です。

最後に表1.5もどきです。
「セル単位の値の計算」では、テキスト7ページ、式(1.13)の実験計画法の制約を参考にして計算式を作成しています。
$$
a_1=-a_2, \ b_1=-b_2, \ (ab)_{11}=-(ab)_{12}=-(ab)_{21}=(ab)_{22}
$$
### セル平均の事後分布の要約統計量 ★表1.5に対応
# 要約統計情報を計算する関数の定義
def calc_stat(x):
return [np.mean(x), np.std(x),
np.quantile(x, 0.025), np.median(x), np.quantile(x, 0.975)]
# 事後分布サンプリングデータの取得
mu_data = idata3.posterior.mu.data.flatten()
a_data = idata3.posterior.a.data.flatten()
b_data = idata3.posterior.b.data.flatten()
ab_data = idata3.posterior.ab.data.flatten()
# セル単位の値の計算
female_non = mu_data - a_data - b_data + ab_data
female_oui = mu_data - a_data + b_data - ab_data
male_non = mu_data + a_data - b_data - ab_data
male_oui = mu_data + a_data + b_data + ab_data
# データフレーム化
pd.DataFrame({'女性・いない': calc_stat(female_non),
'女性・いる': calc_stat(female_oui),
'男性・いない': calc_stat(male_non),
'男性・いる': calc_stat(male_oui)},
index=['EAP', 'post.sd', '2.5%', 'MED', '97.5%']
).T.round(3)【実行結果】
大きく異なる結果になってしまいました。
マイナス値が出てしまったのが痛いです。


モデル4でMCMC
PyMCモデリング その2「モデル4」
続いてモデル4を試します。
最後にどんでん返しを用意しています!
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
モデル3と比べて、$${\mu_{days}}$$の計算が異なっています。
添字$${j}$$は説明変数「性別」の値であり、$${j=0:女性、j=1:男性}$$です。
添字$${j^{\prime}}$$は説明変数「恋人の有無」の値であり、$${j^{\prime}=0:いない、j^{\prime}=1:いる}$$です。
$$
\begin{align*}
\mu &\sim \text{Uniform}(-100, 100) \\
a_j &\sim \text{Uniform}(-100, 100) \\
b_{j^{\prime}} &\sim \text{Uniform}(-100, 100) \\
ab_{jj^{\prime}} &\sim \text{Uniform}(-100, 100) \\
\sigma_e &\sim \text{Uniform}(0, 100) \\
\mu_{days} &= \mu + a_j + b_{j^{\prime}} + ab_{jj^{\prime}} \\
components &= [ \\
&\text{Normal.dist}(\text{mu} =\mu_{days}, \ \text{sigma}=\sigma_e) -12, \\
&\text{Normal.dist}(\text{mu} =\mu_{days}, \ \text{sigma}=\sigma_e) -11, \\
&\quad \vdots \\
&\text{Normal.dist}(\text{mu} =\mu_{days}, \ \text{sigma}=\sigma_e) -1, \\
&\text{Normal.dist}(\text{mu} =\mu_{days}, \ \text{sigma}=\sigma_e) +1, \\
&\quad \vdots \\
&\text{Normal.dist}(\text{mu} =\mu_{days}, \ \text{sigma}=\sigma_e) +11, \\
&\text{Normal.dist}(\text{mu} =\mu_{days}, \ \text{sigma}=\sigma_e) +12 \\
] \\
likelihood &\sim \text{Mixture}(\text{comp\_dist}=components, \ \text{weight}=w) \\
\end{align*}
$$
1.初期値設定
モデル3と同様に混合分布のウエイト(重み)$${w}$$を掲載します。
モデル3で実行済みの場合は、省略可能です。
### 初期値設定
## データのインデックス、カテゴリ変数のインデックスの取得
idx_data = data.index
## 混合分布の混合割合w:観測データ(全122行)ごとにマスク個数分の均等割合を算出
# wの初期化
w = np.zeros((len(data), 24))
# 観測値AVごとに可能なマスク個数を算出(テキストのN()関数が返すAの要素数に相当)
Ns = data['AV'].apply(lambda x: x + 13 if x<=-1 else x + 12 if x<=12 else 24)
# w(numpy配列)の作成
for i, N in enumerate(Ns):
# 配列先頭からマスクの個数までの要素を1/Nにする
w[i, :N] = 1 / N
# wの表示
print('混合割合w: shape=', w.shape)
print(w)【実行結果】省略:モデル3と同じ
2.モデルの定義
モデル4も3つ告白します。
1つ目はモデル3と同様に、カスタム分布関数の定義に自信がありません。
2つ目は月平均視聴日数muDaysの計算に対する新たな不安です。
モデル4では、$${a_j,\ b_{j^{\prime}},\ ab_{jj^{\prime}}}$$のように、説明変数「性別」「恋人の有無」カテゴリ値ごとに効果・交互作用効果のようなパラメータを設定しています。
このモデリングに合理性があるのか、とても不安です。
3つ目はモデル3と同様に、事後分布の要約統計量はテキストとかなり相違しています。
有識者のみなさま「ぜひアドバイスをお願いします!」
### モデルの定義
# カスタム分布関数の定義:正規分布+マスクm ★この正規分布の設定に自信なし
def custom_dist(
mu: pt.TensorVariable,
sigma: pt.TensorVariable,
m: pt.TensorVariable,
size: pt.TensorVariable,
) -> pt.TensorVariable:
return pm.Normal.dist(mu=mu, sigma=sigma, size=size) + m # '+m'に注目
# モデルの定義
with pm.Model() as model4:
### データ関連定義
# coordの定義
model4.add_coord('data', values=data.index, mutable=True)
model4.add_coord('sex', values=['女性', '男性'], mutable=True)
model4.add_coord('lover', values=['いない', 'いる'], mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data['AV'].values, dims='data')
xSex = pm.ConstantData('xSex', value=data['sex'].values, dims='data')
xLover = pm.ConstantData('xLover', value=data['lover'].values, dims='data')
### 事前分布
mu = pm.Uniform('mu', lower=-100, upper=100)
a = pm.Uniform('a', lower=-100, upper=100, dims='sex')
b = pm.Uniform('b', lower=-100, upper=100, dims='lover')
ab = pm.Uniform('ab', lower=-100, upper=100, dims=('sex', 'lover'))
sigmaE = pm.Uniform('sigmaE', lower=0, upper=100)
### 月平均視聴日数muDaysの計算 ★2要因配置の実験計画モデルに合致するか自信なし
muDays = pm.Deterministic('muDays',
mu + a[xSex] + b[xLover] + ab[xSex, xLover],
dims='data')
### 混合分布に含める確率分布の構成の定義
# マスクのfull集合A_full {-12, -11, …, -1, 1, …, 12}
A_full = np.delete(np.arange(-12, 13), 12)
# リスト内包表記で24個(マスク個数分)のカスタム正規分布を生成
components = [
pm.CustomDist.dist(muDays, sigmaE, m, dist=custom_dist) for m in A_full
]
### 尤度の計算:混合分布
likelihood = pm.Mixture('likelihood', w=w[idx_data], comp_dists=components,
observed=y, dims='data')【モデル注釈】
モデル3との違いは「月平均視聴日数muDaysの計算」とそのパラメータの形状です。
$${切片 \mu + a[性別]+ b[恋人の有無]+ ab[性別, 恋人の有無]}$$としています。
パラメータの形状は$${a=(性別),\ b=(恋人の有無),\ ab=(性別,\ 恋人の有無)}$$です。
3.モデルの外観の確認
# モデルの表示
model4【実行結果】
見た目はモデル3と類似しています。
実はmuDaysの中身が異なります。

# モデルの可視化
pm.model_to_graphviz(model4)【実行結果】
パラメータ$${a, b, ab}$$の形状が角丸四角の右隅に描かれています。
coordで指定したデータ名が添えられています。

4.事後分布からのサンプリング
サンプリングの条件はモデル3と同じです。
ただし、処理時間が「155分」かかりましたのでご注意くださいませ。
### 事後分布からのサンプリング(サイズを縮小しています) 155分
with model4:
idata4 = pm.sample(draws=100000, tune=50000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
5.サンプリングデータの確認
$${\hat{R}}$$、要約統計量、トレースプロットを確認しましょう。
まずは$${\hat{R}}$$の確認から。
### r_hat>1.1の確認
rhat_idata4 = az.rhat(idata4)
(rhat_idata4>1.1).sum()【実行結果】
$${\hat{R} \leq1.1}$$であり、収束条件を満たしています。

続いて要約統計量。
# 推論データの要約統計量の表示 ★表1.3に対応(MAP・MEDを除く)
var_names = ['mu', 'a', 'b', 'ab', 'sigmaE']
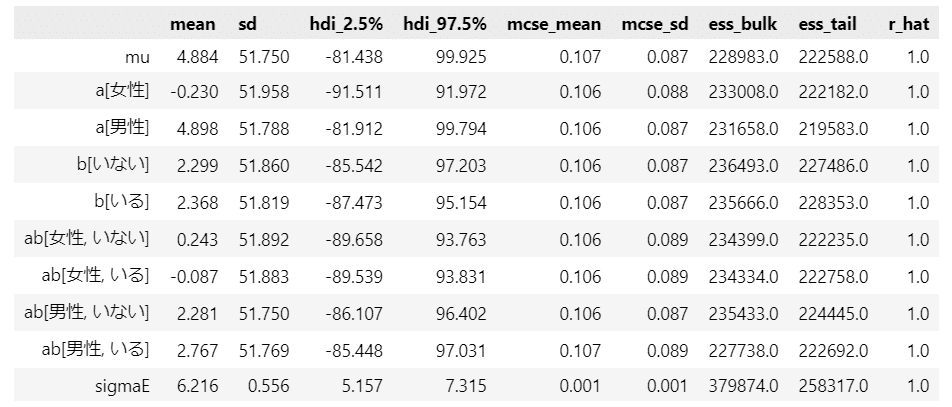
pm.summary(idata4, hdi_prob=0.95, var_names=var_names)【実行結果】
coordを設定したことで「女性」・「男性」、「いない」・「いる」を表示できました。
小さいことかもですが、分かりやすくなりました。
統計値は、テキスト表1.3と比べて、$${\mu}$$が小さく、その代わりに、各パラメータで補うような感じになりました。
各パラメータの標準偏差sdを見ると、かなりバラツキが大きい印象です。
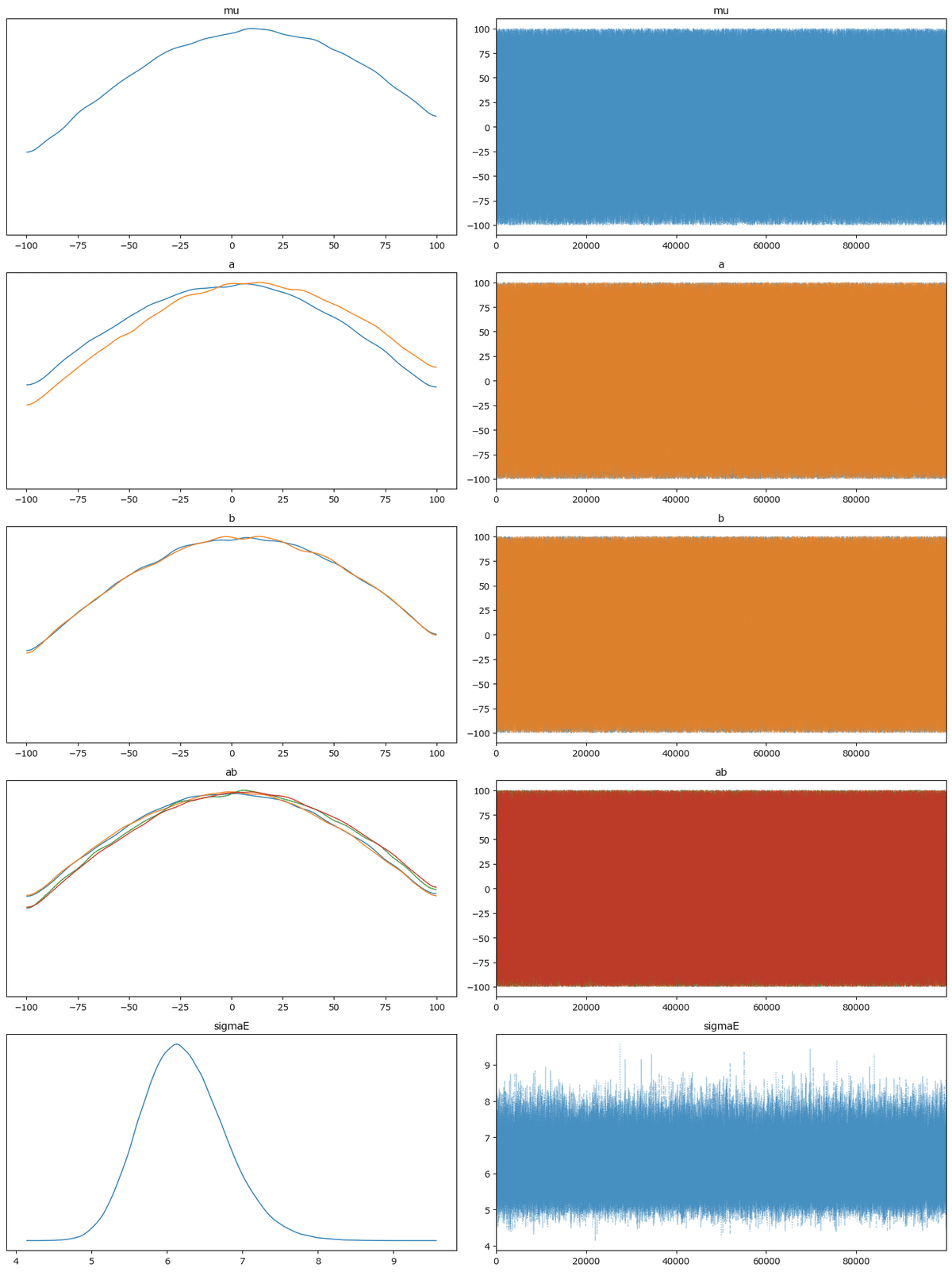
最後にトレースプロットです。
# トレースプロットの描画
pm.plot_trace(idata4, var_names=var_names, combined=True, figsize=(15, 20))
plt.tight_layout();【実行結果】
右のプロットはめっちゃ収束している感じを醸しています。
左のプロットは各パラメータの値の両端の途切れ感が否めません。
ハイパーパラメータの範囲を$${[-100, 100]}$$にしていることが両端の途切れに繋がっていると考えられます。
ただし、ハイパーパラメータの範囲を$${[-1000, 1000]}$$に広げても、トレースプロットは似たような形状になります。
6.テキストの図表(図1.2、表1.5)
トレースプロットでだいたい予想がつくかと思いますが、図1.2に相当する描画は途中で見切れています。
### パラメータaのヒストグラム 図1.2に対応
# パラメータa(水準:男性)の事後分布からのサンプリングデータの取得
a_post = idata4.posterior.a.data[:, :, 1].flatten()
# a>0の確率の計算
a_prob = (a_post>0).mean()
# ヒストグラムの描画
plt.hist(a_post, bins=30)
plt.title(f'要因:性別・水準:男性の効果, a2>0の確率{a_prob:.1%}')
plt.show()【実行結果】

### パラメータbのヒストグラム 図1.2に対応
# パラメータb(水準:いる)の事後分布からのサンプリングデータの取得
b_post = idata4.posterior.b.data[:, :, 1].flatten()
# b>0の確率の計算
b_prob = (b_post>0).mean()
# ヒストグラムの描画
plt.hist(b_post, bins=30)
plt.title(f'要因:恋人・水準:いるの効果, b>0の確率{b_prob:.1%}')
plt.show()【実行結果】

最後に表1.5もどきです。
実は結果に少々自信があります!
### セル平均の事後分布の要約統計量 ★表1.5に対応
# 要約統計情報を計算する関数の定義
def calc_stat(x):
return [np.mean(x), np.std(x),
np.quantile(x, 0.025), np.median(x), np.quantile(x, 0.975)]
# 事後分布サンプリングデータの取得
mu_data = idata4.posterior.mu.data.flatten()
a0_data = idata4.posterior.a[:, :, 0].data.flatten()
a1_data = idata4.posterior.a[:, :, 1].data.flatten()
b0_data = idata4.posterior.b[:, :, 0].data.flatten()
b1_data = idata4.posterior.b[:, :, 1].data.flatten()
ab00_data = idata4.posterior.ab[:, :, 0, 0].data.flatten()
ab01_data = idata4.posterior.ab[:, :, 0, 1].data.flatten()
ab10_data = idata4.posterior.ab[:, :, 1, 0].data.flatten()
ab11_data = idata4.posterior.ab[:, :, 1, 1].data.flatten()
# セル単位の事後分布のサンプリングデータの加工
female_non = mu_data + a0_data + b0_data + ab00_data
female_oui = mu_data + a0_data + b1_data + ab01_data
male_non = mu_data + a1_data + b0_data + ab10_data
male_oui = mu_data + a1_data + b1_data + ab11_data
# データフレーム化
pd.DataFrame({'女性・いない': calc_stat(female_non),
'女性・いる': calc_stat(female_oui),
'男性・いない': calc_stat(male_non),
'男性・いる': calc_stat(male_oui)},
index=['EAP', 'post.sd', '2.5%', 'MED', '97.5%']
).T.round(2)<分析結果を早く見たい方はここから>
【実行結果】
テキスト表1.5に近い結果を得られました(ホッとしました!)
モデル4のモデリングが妥当ならば、この要約統計量で「月当たりの視聴回数」の分析を進めたいです!


「セル単位の事後分布のサンプリングデータ」のヒストグラムを描画します。
### 事後分布データのセル平均を描画
# ビンを指定 最小値-0.018, 最大値28.89
bins = np.arange(-1, 30)
# 描画領域の指定
plt.figure(figsize=(8, 4))
# ヒストグラムの描画(女性・いない)
plt.hist(female_non, bins=bins, histtype='stepfilled', density=True, alpha=0.3,
label='女性・いない')
# ヒストグラムの描画(女性・いる)
plt.hist(female_oui, bins=bins, histtype='step', density=True, label='女性・いる')
# ヒストグラムの描画(男性・いない)
plt.hist(male_non, bins=bins, histtype='stepfilled', density=True, alpha=0.3,
label='男性・いない')
# ヒストグラムの描画(男性・いる)
plt.hist(male_oui, bins=bins, histtype='step', density=True, label='男性・いる')
# 修飾
plt.xticks(bins)
plt.title('月当たりのR18映像視聴日数')
plt.xlabel('月当たりの視聴日数')
plt.ylabel('確率密度')
plt.legend()
plt.show()【実行結果】

【分析】
大学生のみなさん、この日にち感はいかがでしょう?
女性の月当たり視聴日数は、恋人がいない=7.2日、いる=6.93日です。
週1.5日程度、視聴しているという値です。
女性は恋人がいない方が視聴日数が大きい結果となりました。
男性の月当たり視聴日数は、恋人がいない=14.36日、いる=14.92日です。
月の半分で視聴しているという値です。
男性は恋人がいる方が視聴日数が大きい結果となりました。

<分析結果を早く見たい方はここまで>
7.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
モデル4のidata4をpickleで保存します。
### idataの保存 pickle
file = r'idata4_ch01.pkl'
with open(file, 'wb') as f:
pickle.dump(idata4, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata4_ch01.pkl'
with open(file, 'rb') as f:
idata4_load = pickle.load(f)以上で第1章は終了です。
以下は省略いたしました。
・研究仮説が正しい確率(PHC)の算出と図1.3、図1.4
・要員計画モデルの分散説明率の事後分布の算出と表1.4
・$${i}$$行のセル平均が$${j}$$列のセル平均より大きい確率の算出と表1.6

おわりに
シリーズ第1回はいかがでしたか?
個人的にはとてもスッキリした気分でこの章を書きました。
実はR・StanのベイズモデルをPyMCに翻訳するのは人生初の取り組みなのですが、最初の章がいきなり超難問!
マスクと混合分布の実現方法が簡単に見つからず、PyMC公式サイトを眺めながら10日くらい悩んでいたところ、突如、天からアイデアが舞い降りてきたのです!
データ1件ごとに24個の重みを設定すれば、混合分布に含める確率分布を24個に固定化できるかも!
事後分布の食い違いをご覧頂いてお分かりのとおり、私が書いた自己流PyMCモデルが適切なのかは定かではありません。
ただ、四六時中マスクに考えを巡らせて何とか一定のモデルに到達できたこと、ベイズモデリングの気持ちに近づけたことから得た喜びは何ものにも代えがたいのです。
このような楽しい機会を作ってくださったテキスト「たのしいベイズモデリング」の著者のみなさまに、心より感謝申し上げます。
ありがとうございます!
この記事は未だトライアルの位置づけです。
どんどんブラッシュアップして、PyMC仲間のみなさまにベイズモデリングをPyMCで楽しんでいただけるように精進いたします。

シリーズの記事
次の記事
前の記事

目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ(お題)を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます!
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。
最後までお読みいただきまして、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
