実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で①線形回帰モデル

「PythonのMCMCライブラリPyMC」章

テキスト「PythonのMCMCライブラリPyMC」の執筆者
渡辺祥則 先生

---

この記事は、テキストの「PythonのMCMCライブラリ PyMC」章の例題１「線形回帰モデルのベイズ推定」の実践を取り扱います。
初学者に優しい単回帰モデルをお借りして、自分用の入門編のつもりで原稿を書きました。
統計モデル、機械学習モデルの回帰分析と比べながら、PyMC Ver.5 のベイズモデリングを実践いたします。

「観測値が回帰式（線形予測子）を平均パラメータに持つ正規分布に従う」王道のモデリング。
ベイズモデリング応用のための基本・土台・基礎（と私が勝手に思っている）を目一杯楽しんでまいりましょう！

はじめに

---

岩波データサイエンスVol.1の紹介

この記事は書籍「岩波データサイエンス vol.1」（岩波書店、以下「テキスト」と呼びます）の特集記事「ベイズ推論とMCMCのフリーソフト」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。

岩波データサイエンス Vol.1

テキストは、2015年10月に発売され、ベイズモデリングの様々なソフトウェアを用いたモデリング事例を多数掲載し、ベイズモデリングの楽しさを紹介する素晴らしい書籍です。
入門的なモデルから2次階差を取り扱う空間モデルまで、幅広い難易度のモデルを満喫できます！

このシリーズは、テキストのベイズモデルをPyMC Ver.5に書き換えて実践します。

引用表記

この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「岩波データサイエンス vol.1」
第９刷、編者 岩波データサイエンス刊行委員会 　岩波書店

記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます！

かわいいフリー素材集

PyMC環境の準備

Anacondaを用いる環境構築とGoogle ColaboratoryでPyMCを動かす方法について、次の記事にまとめています。
「PyMCを動かすまでの準備」章をご覧ください。

PythonとPyMCの最新化
テキストのPyMCのバージョンはVer.3です。
また、テキスト発行の2015年から現在2024年までの約10年で、Python及び各種パッケージの利用方法が変わっています。
そこでこの記事では、テキスト掲載のPython＆PyMC3コードを自己流Python＆PyMC5コードに変換することを、実践事項の１つに取り上げようと思います。

例題１ 線形回帰モデルのベイズ推定

---

次の式のような、切片$${\alpha}$$、傾き$${\beta}$$、誤差$${\varepsilon}$$を用いて表される単回帰モデルを実践します。

$$
y=\alpha+\beta x + \varepsilon, \quad \varepsilon \sim \text{Normal}(\mu, \sigma^2)
$$

1. 準備

「PythonのMCMCライブラリPyMC」章で利用するパッケージをインポートします。

### インポート

# ユーティリティ
import pickle

# 数値・確率計算
import pandas as pd
import numpy as np

# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az

# 回帰分析
import scipy.stats as stats
import statsmodels.formula.api as smf
from sklearn.linear_model import LinearRegression

# 分類タスク
from sklearn.metrics import classification_report

# WEBアクセス
import requests

# yfinance株価データ取得
from pandas_datareader import data as pdr
import yfinance as yf

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

2. データの作成

テキストと同じ乱数作成方法を用いて、説明変数$${X}$$と目的変数$${Y}$$の値をそれぞれ40個作成します。
$${X}$$は０から10の一様分布乱数です。
$${Y}$$は$${4+20X+誤差}$$です。誤差は平均0、標準偏差16の正規分布乱数です。
最後に$${X,Y}$$の散布図を描画します。テキスト図1のアップデート版です。

### データの作成

## 初期値設定
# 乱数生成器の作成
rng = np.random.default_rng(seed=123)
# 初期値
N = 40        # 標本サイズ
alpha = 4     # 切片
beta = 20     # 傾き
sd = 16       # 標準偏差

## データ作成
# 説明変数Xの作成（一様分布乱数）
X = rng.uniform(low=0, high=10, size=N)
# 目的変数Yの作成 Y = 4 + 20X + 誤差（正規分布N(0,16)乱数）
Y = alpha + beta * X + rng.normal(loc=0, scale=sd, size=N)
# データフレーム化
data1 = pd.DataFrame({'X': X, 'Y': Y})

# データの可視化 ※図1に相当
sns.lmplot(data=data1, x='X', y='Y', height=3, aspect=1.5,
           line_kws={'color': 'tomato'}, scatter_kws={'alpha': 0.5})
plt.xlim(0, 10)
plt.title(f'相関係数: {data1.corr().iloc[0, 1]:.3f}')
plt.grid(lw=0.5);

【実行結果】
seabornのlmplotを利用すると、回帰直線も描いてくれます。
もはや、ベイズなどしなくともseabornでいいじゃん、かもですｗ
相関係数はpandasのcorr関数を利用して算出しました。

脱線予告

テキストのベイズモデルから脱線します！
ベイズ回帰分析に入る前に、Pythonで実践できる３つの統計・機械学習方面の単回帰モデルのツアーを敢行いたします！
そんなのいらない！って方は、ベイズモデルの章に飛んでください🚀

3. 線形最小二乗回帰の計算

scipy.statsのlinregressを利用して、切片・傾き等のパラメータを計算します。
「result_lr = stats.linregress(x=data1['X'], y=data1['Y'])」のたった１行で、単回帰のパラメータが「result_lr」に格納されるのです。簡潔です！

### scipy.statsのlinregressで単回帰分析

# 単回帰分析の実行
result_lr = stats.linregress(x=data1['X'], y=data1['Y'])

# 単回帰分析の結果表示
print(f'回帰式        : y = {result_lr.intercept:.3f} + {result_lr.slope:.3f}x')
print(f'相関係数      : {result_lr.rvalue:.3f}')
print(f'傾きのp値     : {result_lr.pvalue:.3f}')
print(f'傾きの標準誤差: {result_lr.stderr:.3f}')
print(f'切片の標準誤差: {result_lr.intercept_stderr:.3f}')

【実行結果】

回帰式に注目します。
切片$${\alpha=0.057}$$は、データ生成に用いた$${\alpha=4}$$とかなり離れている感じがします。
一方で、傾き$${\beta=20.674}$$は、データ生成に用いた$${\beta=20}$$にとても近い値です。
傾きの検定の$${p}$$値は$${0.000}$$なので、傾き$${20.674}$$は有意です。
傾きが０とは言えない、という意味で有意です。

4. 統計モデル

statsmodelsで最小二乗法による線形回帰分析を行います。
１行目だけで回帰分析は完了です。こちらも簡潔ですね！

### 単回帰分析（最小二乗法）の実行
ols_result = smf.ols(formula='Y ~ 1 + X', data=data1).fit()
display(ols_result.summary())

【実行結果】

統計的な判断材料がたくさん掲載されています。

統計的にモデルの当てはまり具合を見るときに用いる指標の例
・決定係数$${R^2}$$(R-squared)：0.953
・モデル全体の$${F}$$統計検定量の$${p}$$値(Prob (F-statistic))：8.64e-27

この数値から、モデルの当てはまりが良い、回帰による変動の効果が有意である、という声が聞こえてきそうです。
また、自己相関、残差の正規性などを確認する指標も記載されていますが、この記事では深入りしないようにします。
単回帰分析（統計検定２級レベル）にご興味ある方は、次の記事をご覧くださいませ。

ところで中段あたりに、傾き（X）と切片（Intercept）の値（coef）が掲載されています。
「3. 線形最小二乗回帰の計算」と同じ結果です。
両方とも最小二乗法で計算しているので、一致するのは当然かもです。

回帰分析結果を格納している「ols_result」から$${X}$$を回帰式に当てはめて得られる$${Y}$$の予測値「fittedvalues」を描画してみましょう。

### 回帰直線の描画
# 描画領域の指定
plt.figure(figsize=(5, 3))
# 観測値の散布図の描画
plt.scatter(data1.X, data1.Y, alpha=0.5, label='観測値')
# 回帰直線の描画
plt.plot(data1.X, ols_result.fittedvalues, color='tab:red', label='OLS')
# 修飾
plt.title(f'$y$={ols_result.params[0]:.3f}+{ols_result.params[1]:.3f}$x$')
plt.xlim(0, 10)
plt.grid(lw=0.5)
plt.legend();

【実行結果】
赤い線がstatsmodelsで計算した回帰直線です。
seabornと同じですね（信頼区間は表示していません）。

5. 機械学習モデル

scikit-learnのLinearRegressionを利用して、機械学習的に回帰分析してみます。
「model_lr = LinearRegression().fit(data1[['X']], data1['Y'])」のたった１行で、単回帰の各種情報が「model_lr」に格納されるのです。簡潔です！

### 機械学習の線形回帰の実行

# モデルのインスタンスの生成と学習（全データ使用）
model_lr = LinearRegression().fit(data1[['X']], data1['Y'])

# 主な結果の表示
print(f'切片       :{model_lr.intercept_:.3f}')
print(f'傾き       :{model_lr.coef_[0]:.3f}')
print(f"決定係数R^2:{model_lr.score(data1[['X']], data1['Y']):.3f}")

【実行結果】
切片、傾き、決定係数は、今まで見てきた結果と同じ値です。

回帰モデル「model_lr」に説明変数$${X}$$を与えて予測を実行し、回帰直線を描画してみましょう。

### 回帰直線の描画
# 描画領域の指定
plt.figure(figsize=(5, 3))
# 観測値の散布図の描画
plt.scatter(data1.X, data1.Y, alpha=0.5, label='観測値')
# 回帰直線の描画
plt.plot(data1.X, model_lr.predict(data1[['X']]), color='tab:red',
         label= 'LinearRegression')
# 修飾
plt.title(f'$y$={model_lr.intercept_:.3f}+{model_lr.coef_[0]:.3f}$x$')
plt.xlim(0, 10)
plt.grid(lw=0.5)
plt.legend();

【実行結果】
statsmodelsのときと同じ描画になりました（当たり前）。

機械学習というと「テストデータを用いたモデルの精度評価や、未知データに対する予測」が重要視されていると思います。
この記事では、Pythonの様々なパッケージを使って単回帰モデルを簡単に構築できることを示すことに重点を置いていますので、モデル評価・予測には踏み込まないことにします。

ここまでのコード実行例をご覧いただき、簡単に回帰分析ができることをご実感いただけたでしょうか。

それでは道草はここまでにして、いよいよベイズモデルに移ります。
いざ本丸へ！

ベイズモデル

---

1. 前説

ベイズモデリングといえば、データをおおらかな包容力をもって語れるように、変数と確率分布をマッチングして確率分布群を組み合わせることが醍醐味です！
回帰式$${y = \alpha + \beta x}$$をどのようにモデルに組み込むのか、も楽しみですね！

■ モデル数式
テキストのモデルを引用いたします。

$$
\begin{align*}
y &\sim \text{Normal}\ (\text{mu}=\beta x + \alpha,\ \text{sigma}=\sigma) \\
 \\
\alpha &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=20) \\
\beta &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=20) \\
\sigma &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=1) \\
\end{align*}
$$

テキストのPyMCコードを一部改変して引用

確率分布には、正規分布$${\text{Normal}}$$と一様分布$${\text{Uniform}}$$の２つが用いられています。

目的変数$${y}$$は正規分布に従っています。
$${\sim}$$の記号を「従っている」と読み、左側の目的変数の確率分布が右側の正規分布であることを示しています。
正規分布には平均$${\text{mu}}$$と標準偏差（※）$${\text{sigma}}$$の２つのパラメータがあります。
$${\text{mu}}$$には回帰式$${\beta x + \alpha}$$が指定されています。
$${\text{sigma}}$$には別の変数$${\sigma}$$が指定されています。
「目的変数$${y}$$は、平均的には回帰式$${\beta x + \alpha}$$であり、$${\sigma}$$のばらつき＝誤差があって、正規分布しているよ」ということです。
（※）正規分布のばらつきは一般的に分散$${\sigma^2}$$を用いますが、PyMCの正規分布クラスでは標準偏差を用います。

■ 確率分布の可視化
正規分布と一様分布の形状を見てみましょう。

### 正規分布と一様分布の確率密度関数の描画

## 描画用データの作成
# x軸の値の作成
x_plot = np.linspace(-4, 4, 1001)
# 正規分布の確率密度関数の値の作成
y_norm = stats.norm.pdf(x_plot, loc=0, scale=1)
# 一様分布の確率密度関数の値の作成
y_uniform = stats.uniform.pdf(x_plot, loc=-2, scale=4)

## 描画
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 3))
# 正規分布の確率密度関数の描画
ax1.plot(x_plot, y_norm)
ax1.axvline(0, color='tab:red', ls='--', label='平均')
ax1.set(title='正規分布')
ax1.set(xticks=[], yticks=[])
ax1.legend()
# 一様分布の確率密度関数の描画
ax2.plot(x_plot, y_uniform)
ax2.axvline(-2, color='tab:red', ls='--', label='lower')
ax2.axvline(2, color='tab:orange', ls='--', label='upper')
ax2.set(title='一様分布')
ax2.set(xticks=[], yticks=[])
ax2.legend();

【実行結果】

■ 正規分布の形状とベイズモデルの変数の関係
正規分布の平均値はベル型の頂点の位置にあります。
平均的に回帰式$${\beta x + \alpha}$$が当てはまる、ということになります。
左右のなだらかなカーブに沿って$${y}$$がばらつくのですが、ばらつき方を決めるのが$${\sigma}$$なのです。
回帰式の切片$${\alpha}$$と傾き$${\beta}$$の分布は、平均が０，標準偏差が20の正規分布が指定されています。

■ 一様分布の形状とベイズモデルの変数の関係
$${\sigma}$$の分布には一様分布を指定しています。
左側の下端$${\text{lower}}$$と右側の上端$${\text{upper}}$$の間の青い線で囲われている領域の値のどれもが$${\sigma}$$の値になりえるのです。
下端・上端に大きな値を用いると、自由領域が広がり、無の境地になるんです（前振り）。

■ 正規分布を指定すること、一様分布を指定すること
正規分布と比べて、一様分布の方が変数の取り得る値が自由なのです。
一様分布と比べて、正規分布の方が変数の取り得る値に縛りがかかっているのです。
したがいまして、パラメータ$${\alpha,\ \beta,\ \sigma}$$のうち、$${\alpha,\ \beta}$$の方が「正規分布」という確率の情報に縛られています。
$${\sigma}$$の方が自由で無制限であり、正規分布と比べると確率の情報が無いです。「無情報」なのです。
目的変数$${y}$$以外のパラメータ$${\alpha,\ \beta,\ \sigma}$$に指定する確率分布は「パラメータの事前分布」と呼ばれます。
無情報の事前分布は「無情報事前分布」と呼ばれます。

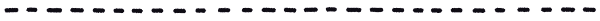
2. モデルの定義

自己流PyMCモデルは次のように定義しました。

$$
\begin{align*}
y &\sim \text{Normal}\ (\text{mu}=\mu,\ \text{sigma}=\sigma) \\
 \\
\mu &= \alpha + \beta x \\
 \\
\alpha &\sim \text{Uniform}\ (\text{lower}=-100,\ \text{upper}=100) \\
\beta &\sim \text{Uniform}\ (\text{lower}=-100,\ \text{upper}=100) \\
\sigma &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\end{align*}
$$

テキストのモデルと比較すると・・・

• 回帰式の部分を外に出して$${\mu}$$に代入しました。
  後で$${\mu}$$のサンプリングデータを利用したいからです。

• $${\alpha,\ \beta}$$の確率分布には、$${-100}$$～$${100}$$の範囲の広い一様分布を指定しました。
  また、$${\sigma}$$の一様分布も上端の範囲を$${100}$$に広げました。
  すべてのパラメータの事前分布に「無情報」を意識してみました。

PyMCのモデル定義に進みましょう。
回帰分析に特化した処理を持つ統計モデルや機械学習モデルと比べると、定義内容が多いです。
「パラメータごとに確率分布を指定すること」が定義内容を多くする要因の一つだと思います。

### モデルの定義
with pm.Model() as model1:
    
    ### データ関連定義
    ## coordの定義
    # 観測データのインデックス
    model1.add_coord('data', values=data1.index, mutable=True)
    
    ## dataの定義
    # 観測値Y
    Y = pm.ConstantData('Y', value=data1['Y'].values, dims='data')
    # 説明変数X
    X = pm.ConstantData('X', value=data1['X'].values, dims='data')

    ### 事前分布
    # 切片α
    # alpha = pm.Normal('alpha', mu=0, sigma=20)     # テキストの事前分布
    alpha = pm.Uniform('alpha', lower=-100, upper=100)
    # 傾きβ
    # beta = pm.Normal('beta', mu=0, sigma=20)       # テキストの事前分布
    beta = pm.Uniform('beta', lower=-100, upper=100)
    # 標準偏差
    # sigma = pm.Uniform('sigma', lower=0, upper=1)  # テキストの事前分布
    sigma = pm.Uniform('sigma', lower=0, upper=100)

    ### 線形予測子
    mu = pm.Deterministic('mu', alpha + beta*X, dims='data')
    
    ### 尤度
    y = pm.Normal('y', mu=mu, sigma=sigma, observed=Y, dims='data')

モデルの内容を表示・可視化してみましょう。
モデル名 model1 とタイプするとモデルの数式の概要が表示されます。

### モデルの表示
model1

【実行結果】

続いてモデルを可視化します。
１行のコードでグラフ形式の可視化ツール「Graphviz」に自動連携して、変数の関係を図示してくれます！

### モデルの可視化
pm.model_to_graphviz(model1)

【実行結果】
データやパラメータの繋がりが示されます。
alphaとbetaとXでmuが計算される様子がよく分かります。
丸い形状の変数には「確率分布」が併記されます。
データ値を示す変数はグレー色が付いています。

3. MCMCの実行と収束の確認

■ MCMC
いよいよベイズプログラミングの真骨頂 MCMC の実行です。
マルコフ連鎖=chainsを4本、バーンイン期間=tuneを1000、利用するサンプル=drawを１chainあたり1000に設定して、合計4000個の事後分布からのサンプリングデータを生成します。テキストの指定数とは異なっています。

サンプリングデータは idata1 に格納されます。
PyMC3 のころは変数名に trace を用いられていましたが、PyMC5の現在は idata を用いることが多いようです。
arviz の InferenceData（推論データ）と関係がありそうです。

サンプル方法に numpyro を指定しています。処理速度が早くなります。
numpyro を使わない場合は「nuts_sampler='numpyro',」を削除します。

### 事後分布からのサンプリング 20秒
with model1:
    idata1 = pm.sample(draws=1000, tune=1000, chains=4, random_seed=1234,
                       nuts_sampler='numpyro', target_accept=0.8)

【実行結果】
処理時間は約20秒です。

■ $${\hat{R}}$$で収束確認
収束の確認をします。
指標$${\hat{R}}$$（あーるはっと）の値が$${1.1}$$以下のとき、収束したこととします。
次のコードではしきい値を$${1.01}$$にキツく設定して、$${\hat{R}>1.01}$$のパラメータの個数をカウントします。
個数が０ならば、$${\hat{R} \leq1.01}$$なので収束したとみなします。

### r_hat>1.1の確認
# 設定
idata_in = idata1        # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】
$${\hat{R}>1.01}$$のパラメータは０個でした。
$${\hat{R} \leq1.1}$$なので収束したとみなします。

■ $${\hat{R}}$$の値把握と事後統計量の表示

### 事後統計量の表示
pm.summary(idata1, hdi_prob=0.95)

【実行結果】
MCMCでサンプリングデータを生成したすべてのパラメータについて、統計量や診断情報が一覧表示されました。
右端の$${\hat{R}}$$（r_hat）はすべて$${1.0}$$です。
上３行が注目するパラメータ$${\alpha,\ \beta,\ \sigma}$$です。
meanはサンプリングデータの平均値、sdはばらつき下限、HDIは95%の確率で収まる範囲です。

■ トレースプロットで収束確認
トレースプロットを描画します。
テキストの図2に該当します。
こちらの図でも収束の確認を行えます。

### トレースプロットの描画 ※図2に相当
pm.plot_trace(idata1)
plt.tight_layout();

【実行結果】
左の曲線は、４本のマルコフ連鎖の分布です。
４本の曲線がほぼ同じ分布を描いているので、サンプリングデータが同一の分布から生成されたことが推察できます。
右のノイズみたいな図は、均等に乱雑に描画されています。
この状態は収束していると推察できます。
均等・乱雑ではなくて、何らかの傾向を示すような描画の場合は収束を疑います。

$${\hat{R}}$$とトレースプロットから、分布の収束が確認できましたので、MCMCのサンプリングデータを用いて、推論を継続できます！
やったね！

テキストではパラメータの事前分布に正規分布で一定の縛り（何らかの事前情報の投入）を行っていましたが、こちらのモデルは一様分布を適用しました。
この事前分布の変更が悪い影響をもたらしたら嫌だな～と思っていたので、収束して一安心です！

■ 事後予測プロットでモデルの良し悪しを確認
もうひとつのプロットで推論の良し悪しを確認してみましょう。
目的変数$${y}$$の事後予測サンプリングを行ってグラフで可視化します。
事後分布からのサンプリング（MCMCのこと）では事後分布を得て「パラメータ」を推論します。
事後予測では、得られた事後分布を元にして「目的変数」を予測しちゃおうってことなのです！

### 事後予測サンプリングの実行
with model1:
    idata1.extend(pm.sample_posterior_predictive(idata1, random_seed=1234))

【実行結果】

### 事後予測プロットの描画
pm.plot_ppc(idata1, num_pp_samples=100, random_seed=123);

【実行結果】
いい感じの図になっていると思います。

黒線が目的変数$${Y}$$の観測値、オレンジの点線が目的変数の事後予測の平均値です。
２つの峰を描くカーブの部分は、観測値と事後予測値の形状がよく似ていて重なって見えます。
青い細線は、事後予測サンプリングデータから100個を取り出して描画したものです。
オレンジ線と比べると少々拡散気味ではありますが、M字の形状をうまく描けているのではないでしょうか。

まとめますと、今回のベイズモデルは目的変数をそこそこ表現できていると思います！

4. 分析

テキストの図3で示されている「フォレストプロット」を描画しましょう。

### フォレストプロットの描画 ※図3に相当
ax = pm.plot_forest(idata1, combined=True, hdi_prob=0.95, r_hat=True,
                     figsize=(5, 3), var_names=['alpha', 'beta', 'sigma'])
ax[0].axvline(0, color='red', ls='--')
plt.tight_layout();

【実行結果】
左のプロットは、切片 alpha、傾き beta、目的変数のばらつき sigmaの３つのパラメータの平均値（中央付近のマル）、50%HDI区間（太線）、95%HDI区間（細線）を示しています。

【パラメータの推論値に関する推察】

１．切片$${\alpha}$$
切片 alpha は 平均$${0}$$付近です。
95%HDI区間が$${-10}$$～$${10}$$と幅広であり、95%の確率で切片が$${-10}$$～$${10}$$に含まれるという推論です。
確かにデータ生成に用いた真値$${4}$$（誰も知らない値）は95%HDI区間に含まれています。

２．傾き$${\beta}$$
傾き beta は約$${20}$$であり、95%HDI区間は激狭です。
データ生成に用いた真値$${20}$$（誰も知らない値）に迫っているので、うまく推論できたように感じます。

３．標準偏差$${\sigma}$$
標準偏差 sigma は平均が約$${14}$$、95%HDIは$${11}$$～$${18}$$程度です。
データ生成に用いた真値$${16}$$（誰も知らない値）は95%HDI区間に含まれています。そこそこの推論水準のように感じます。

お気づきですね！
ベイズはパラメータの推論値を特定の１点だけでなく、例えば95%の確率に収まる区間も推論してくれます。
もちろん10%や50%等の確率も分かります。
統計分野の信頼区間と何が違うの？という疑問に対しては、パラメータは◯◯%の確率でこの範囲になると「胸を張って」言えるのがベイズの真骨頂なのです！
さらに、サンプリングデータを活用して、さまざまな指標を算出することもできます。
MCMCのサンプリングデータは最強なのです（言い過ぎ）

最後に回帰直線を描画しましょう。
MCMCでサンプリングした「正規分布の平均パラメータ mu（$${\mu = \alpha + \beta x}$$）」のデータをプロットします。

### 期待値μの事後分布の描画

## データの作成
mu_samples = idata1.posterior.mu.stack(sample=('chain', 'draw')).data
mu_means = mu_samples.mean(axis=1)
alpha_mean = idata1.posterior.alpha.data.flatten().mean()
beta_mean = idata1.posterior.beta.data.flatten().mean()

## 描画
# 描画領域の指定
plt.figure(figsize=(5, 3))
# 観測値の散布図の描画
plt.scatter(data1.X, data1.Y, alpha=0.5, label='観測値')
# 回帰直線の描画
plt.plot(data1.X, mu_means, color='tab:red', label='$\mu$ の事後平均')
# 95%HDIの描画
az.plot_hdi(data1.X, mu_samples.T, smooth=False, color='tomato',
            fill_kwargs={'alpha': 0.2})
# 95%HDIの凡例用のダミー
plt.fill_between([], [], [], color='tomato', alpha=0.2, label='95%HDI')
# 修飾
plt.title(fr'事後平均：切片$\alpha$={alpha_mean:.3f}, 傾き$\beta$={beta_mean:.3f}')
plt.xlim(0, 10)
plt.grid(lw=0.5)
plt.legend();

【実行結果】
4000個の$${\mu}$$のサンプリングデータから算出した「平均値」を赤い線で、「95%HDI」区間を薄赤色の塗りつぶしで表現しています。
seabornのlmplotみたいですねｗ

95%HDI区間から外れている観測値（青いマル）が多いのは、平均値$${\mu}$$の描画であり、ばらつき$${\sigma}$$を除いた値だからです。
統計モデルや機械学習モデルの回帰分析と同様に（誤差分布に）正規分布を仮定している点で、統計モデルや機械学習モデルと類似した結果になったのだと推察されます。

ばらつき$${\sigma}$$を加味する「$${y}$$の事後予測」のプロットは次のようになります。

### 目的変数yの事後予測の描画

## データの作成
y_samples = idata1.posterior_predictive.y.stack(sample=('chain', 'draw')).data
y_means = y_samples.mean(axis=1)
y_95hdi = az.hdi(y_samples.T, hdi_prob=0.95).T

## 描画
# 描画領域の指定
plt.figure(figsize=(5, 3))
# 観測値の散布図の描画
plt.scatter(data1.X, data1.Y, alpha=0.5, label='観測値')
# 回帰直線の描画
plt.plot(data1.X, y_means, color='tab:red', label='$y$ の事後予測平均')
# 95%HDIの描画
az.plot_hdi(data1.X, y_samples.T, smooth=False, color='tomato',
            fill_kwargs={'alpha': 0.2})
# 95%HDIの凡例用のダミー
plt.fill_between([], [], [], color='tomato', alpha=0.2, label='95%HDI')
# 修飾
plt.xlim(0, 10)
plt.grid(lw=0.5)
plt.legend();

【実行結果】
上の図と比べると95%HDIの幅が広くなりました。
ばらつき$${\sigma}$$が加味されているからでしょう。
観測値はほぼ95%HDI区間に含まれています。
ベイズにやさしく包まれているかのようです。

seabornにこのプロットは描けないでしょう（勝利）
また、パラメータ$${\alpha,\ \beta,\ \sigma}$$についても、$${\mu}$$と同様にMCMCサンプリングデータを用いて、「確率的に」統計量を算出して分析に活用できます。
統計モデル・機械学習モデルとの比較でベイズモデルのいいところの１つは、確率的な分析を容易にできることです。

5. 推論データの保存

pickle で MCMCサンプリングデータ idata1 を保存できます。

### 推論データの保存
file = r'idata1_ch1.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata1, f)

次のコードで保存したファイルを読み込みできます。

### 推論データの読み込み
file = r'idata1_ch1.pkl'
with open(file, 'rb') as f:
    idata1_ch1_load = pickle.load(f)

ベイズ記事は以上です。

次回予告

「PythonのMCMCライブラリ PyMC」章
　例題２「階層ベイズモデル」

結び

---

シリーズ最初の記事は気合が入って長文になりました。
次回からはあっさり軽めのボリュームで挑みたいと思います。
ベイズモデルのPyMC5実装はすでに完了しています。
あとは記事にするだけ！（簡単ではない）

ところで、「PythonのMCMCライブラリ PyMC」章のPython・PyMC3のコードを読んでみると、現時点のPython・PyMC5では見慣れない記述に遭遇します。
技術的な書籍は技術の更新が進むことで、遺産化を免れることができません。
ただ、技術だけでなく技術以外の部分でも含蓄・示唆に富んでいる良書を過去のものにしてしまうのは、もったいないです。
零細ではありますが、先達の資産を現代風にアレンジする「伝承」を続けていきたい所存です。

おわり

---

シリーズの記事

次の記事

前の記事

この記事からはじまります

目次

ブログの紹介

---

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは Ｒ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経 ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。