
高校の二次関数
こんにちは。
今回は数学Iの中でも一番重要な [2次関数] について書いていきます。
[2次関数] といって何を扱うのか、と思う方も多いかもしれませんが、簡単にいうと「放物線」を扱います。これ自体は中学 3 年生で習ってはいますが、平行移動や不等式が絡んでくるので一層ハードになります。
はじめに身につけて欲しいのは、2乗の因数分解を応用した「平方完成」という手法です。不安な人は2乗の展開・因数分解の復習をしておきましょう。これを使うと座標平面上でグラフを描いたときの軸、頂点がはっきりします。x だけの2次式を見たところで 「これが何を表しているか分かった」とはそうそうなりません(かなり慣れたら別ですが)。2 次関数が出てきて何をしたら良いか分からなくなったら「平方完成」することで何か分かるかも。
しかし、これだけでは切り抜けられるはずありません。そこで「場合分け」の出番 です。中学校の数学ではあまり現れないこの手法なので、慣れない人も多いでしょう。 高校数学では(もしかしたら理科でも)しばしば出る手法です。どんどん使いましょう。
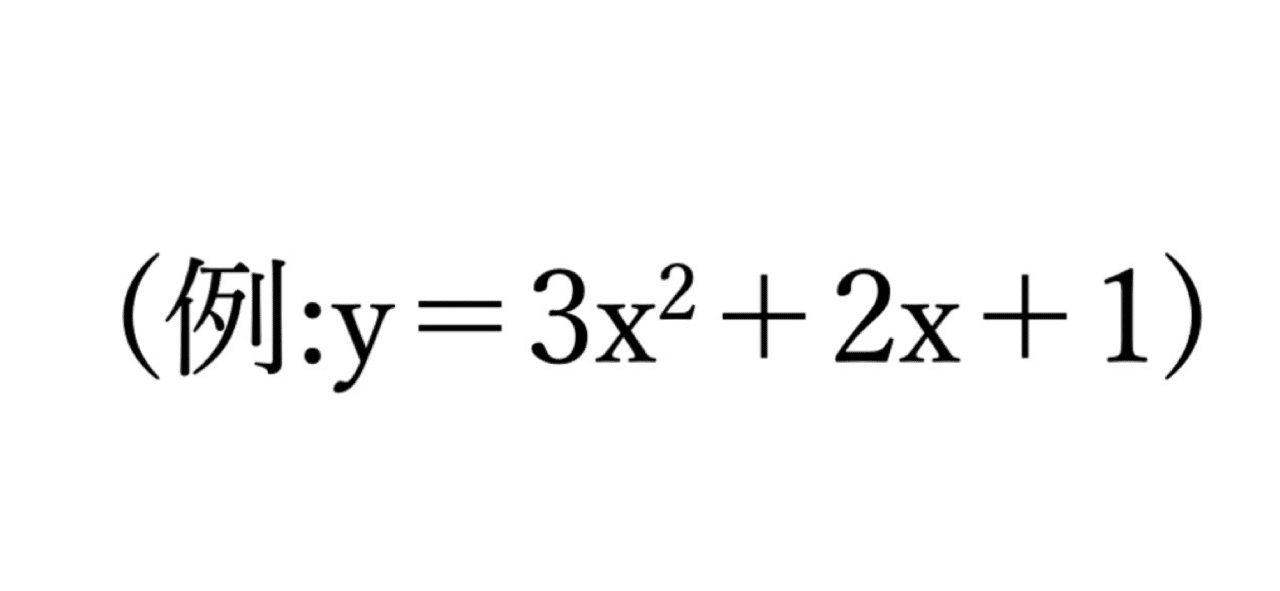
例えば、範囲付の最大値・最小値の問題。放物線の式が 1 つの文字で動いているならば、すぐさま平方完成して最小値はこう、最大値はなし、というように考えられる。しかし、例であげた式のどこかに文字 a を入れて、範囲を指定すると式は一変。a がどの値かを考えて場合分けをする必要があります。場合によっては 5 通りぐらいあります。こういったときは図示も有効です。複雑なものは 1 個ずつ見分けて場合分けをする、 図示をすることでより単純な形ができます。単純化するのがこの分野でのポイントになり ます。
⻑くなったので今回はここでキーボードを打つ手を止めます。次回はこれに方程式や不等式が関わってきます。


clue zemi の詳細・お問い合わせはこちら↓





