
産屋敷の「人の思いは永遠」は本当か。宇宙の巨大数をめぐる科学史
『鬼滅の刃 柱稽古編』について。産屋敷と無惨の会話で気になったので、ツッコミを入れたいと思います。
産屋敷:君の心が、私にはわかるよ。君は、永遠を夢見ている。不滅を夢見ている。
無惨:そのとおりだ。そしてそれは間もなく叶う。禰豆子を手に入れさえすれば。
産屋敷:君の夢は叶わないよ、無惨。
無惨:禰豆子の隠し場所にずいぶんと自信があるようだな。しかし、お前と違い私にはたっぷりと時間がある。
産屋敷:君は、思い違いをしている。
無惨:なんだと。
産屋敷:私は、永遠が何か知っている。永遠というのは、人の思いだ。人の思いこそが、永遠であり、不滅なんだよ。
無惨:くだらん。お前の話には辟易する。
産屋敷:この千年間、鬼殺隊は無くならなかった。可哀想な子どもたちは大勢死んだが、決して無くならなかった。その事実は今、君がくだらないと言った人の思いが不滅であることを証明している。「大切な人の命を理不尽に奪ったものを許さない」という思いは、永遠だ。君は誰にも許されていない。この千年間一度も。
産屋敷の「その事実は今、君がくだらないと言った人の思いが不滅であることを証明している」というセリフを少し細かく見てみましょう。
何を証明しているのか。 「人の思いが不滅であること」を証明している。
何が証明している? 「その事実」が証明している。
その事実とは? 「この千年間、鬼殺隊が無くならなかった」という事実。
つまり、このセリフで産屋敷が言いたかったことはこうなります。
この千年間で鬼殺隊が無くならなかったという事実が、人の思いが不滅であることを証明している
これを、セリフとして表れていない補助前提も含めて論理構造化すると、おそらくこう。
人の思いが鬼殺隊をつくる。
鬼殺隊が無くなっていないのであれば、人の思いも無くなっていない。
「千年、鬼殺隊は無くならなかった」ということは、「千年、人の思いも無くならなかった」ということ。
千年は永遠である。
だから、人の思いも永遠(不滅)である。
私が気なるところはここ。
千年間は永遠である。
果たして、千年は永遠と言えるでしょうか。
さっそく産屋敷の出鼻をくじくのですが、千年は永遠とは言えないでしょう。千年程度の年数では、永遠などとは言っていられないのです。というのも、千年は「永遠」と言うにはあまりにも矮小ですから。
千年とは(文字通り)ケタ違いの巨大数は、夜空に広がっています。宇宙です。古代から現代まで、それぞれの時代に哲学者、観測者、科学者たちは夜空を見上げ、宇宙を観測し、理論をつくってきました。古くは古代ギリシャの時代から、彼らは宇宙に魅入られてきました。
「夜空に光るたくさんの小さな光は何なのだろう」
「太陽はどのくらい遠くになるのだろう」
「宇宙はどのように始まったのだろう」
そんな疑問に答えるべく、彼らは人生を捧げてきたのです。技術を開発し、理論を考え、観測に精を出してきました。
千年を「永遠」などと豪語する産屋敷にはこの本を勧めたい。
ビッグバン宇宙論を巡る科学者たちのノンフィクション。私はこの本が面白くて、いくつもの強調線を紙面に引きつつ5、6回読んでいます。
以下では本書の内容を参照しつつ、5人の人物を中心に、科学史の一旦を紹介します。千や万では収まりきらない、巨大数をめぐる物語。そして、「千年は永遠である」なぞと嘯(うそぶ)く産屋敷の主張を反証したいと思います。
1.太陽の大きさを算出する。エラトステネス
まず紹介するのはエラトステネス。彼は地球の大きさ、月の大きさと地球からの距離、太陽の大きさと地球からの距離を測定しました。驚くべきは、彼の生きた時代です。というのも、彼は紀元前200年代の人なのです。そう、エラトステネスはなんのテクノロジーも無い時代に、観測した事実と思案した理論でもってこれらの偉業を成しました。
(1)シエネの井戸とアレクサンドリアの棒。地球の大きさ
エラトステネスは、アレクサンドリアの図書館長をしていたとき、エジプト南部のシエネという町にある、ある興味深い井戸の話を聞きました。その井戸では一年に一度、太陽が最も空高く上るとき、陽の光が真上から差し込み、井戸の底を照らすのだと言います。つまり、このシエネの井戸は北回帰線上にあり、夏至の日に陽の光はシエネの頭上から降り注ぐ、ということです。それに対して、アレクサンドリアでは夏至の日であっても陽の光が頭上から降り注ぐことはありませんでした。ここからエラトステネスは、目の前の事実と理論で地球の大きさを測定したのです。

陽の光がシエネで井戸の底を照らしたときに、エラトステネスはアレクサンドリアで地面に棒を立て、陽の光と棒がなす角度を測りました。この角度が、地球の中心からシエネとアレクサンドリアに引っ張った線のなす角度と同じなのです。この角度は7.2度だったのだから、丸い地球にとって7.2/360、つまりアレクサンドリアの棒とシエネの井戸の距離は、地球の周長の1/50。次にエラトステネスはアレクサンドリアとシエネの井戸の距離を測ったところ、925,000メートルでした。というわけで、地球の周長は46,250,000メートルということになります。地球の直径は、これをπで割った数になります。
(2)相似の三角形の比。月の大きさと地球からの距離
地球の周長を手に入れたエラトステネにとって、月までの大きさと地球からの距離を導き出す準備は整っていました。というのも、月の直径は地球の直径の1/4ということはわかっていたからです。エラトステネス以前の科学者によって、すでに調べられていたのです。月食のときに月にかかる地球の影の大きさから、月の直径は地球の直径の1/4であることがわかっていました。月食の日、月に地球の影ができてから月が完全に隠れるまでが50分。月に地球の影ができてから、月が影で完全に隠れ、また陽の光を受けるまで200分。したがって、地球の直径は月の直径の4倍になります。

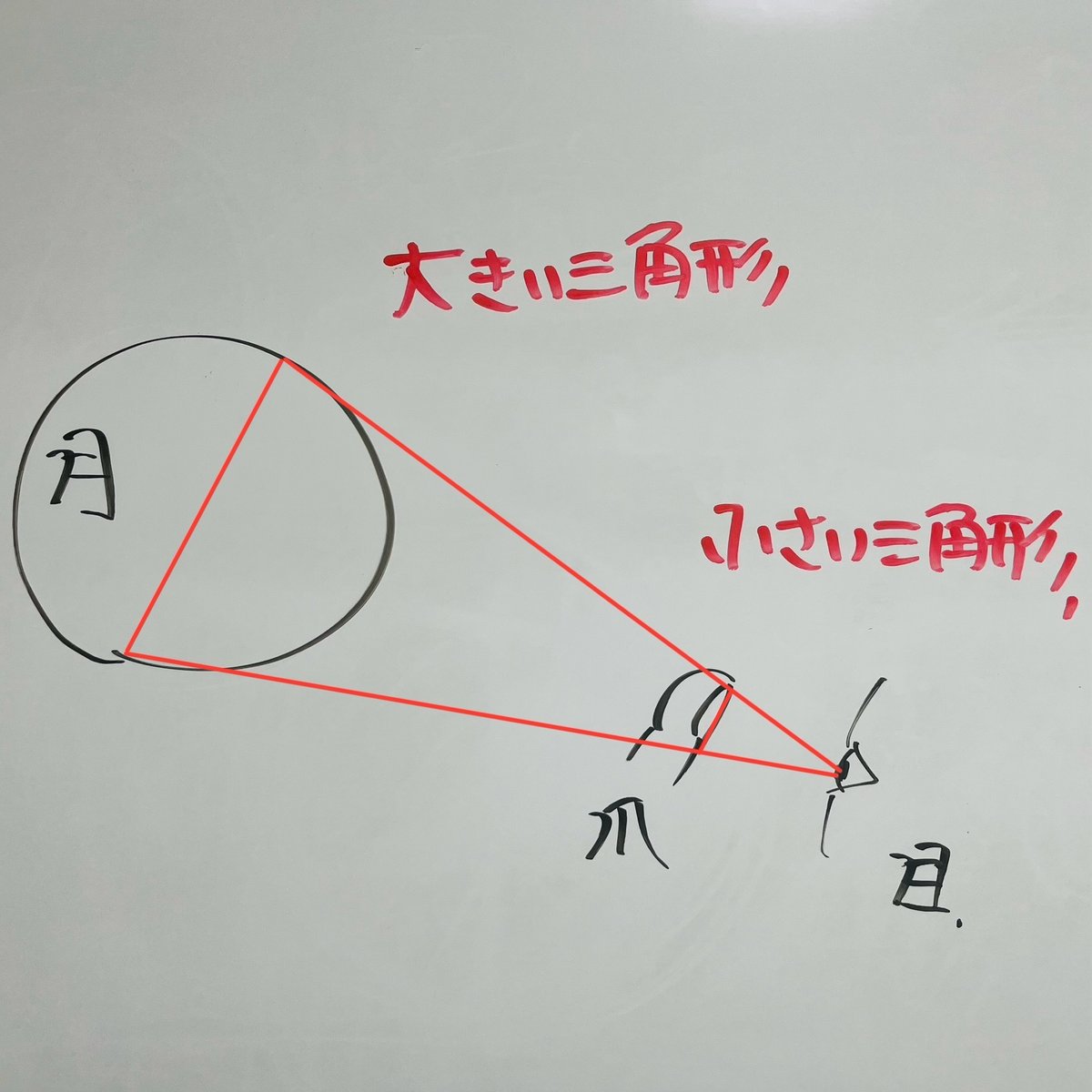
次に月までの地球からの距離。月までの距離の測定方法は、目と指の爪で三角形を作る方法が紹介されていました。まず満月に向かって腕を伸ばし、片目を閉じます。そして人差し指を立て、爪の上下と満月がほぼ同じ大きさなのを確認します。腕の長さと爪の長さの比(だいたい100対1)は、月までの距離と月の直径の比に等しいはず。このことから、月までの距離は月の直径の約100倍と計算できます。
(3)直角三角形の配置。太陽の大きさと地球からの距離
太陽までの地球からの距離は、アリスタルコスの思想を使います。アリスタルコスは漫画「チ。ー地球の運動についてー」でも触れられていたとおり、地動説を唱えた古代ギリシャの天文学者です。
アリスタルコスは、月の光は陽の光を反射したものであり、月が半月になるのは、太陽と月と地球が直角三角形の配置になった時だと考えましあ。この配置の時にアリスタルコスは、地球と太陽、地球と月を結ぶ線がなす角度を測り、87度との結果を得ていました。これは太陽が月よりも約20倍遠くにあることを意味します。ここからエラトステネスは、太陽までの距離を求めました。地球から月までの距離はすでに計算していたことから、太陽までの距離を求めることができたのです。

最後に太陽の大きさ。これを計算する際に使うのは、皆既日食の際の、月が太陽をすっぽり覆い隠すという事実です。つまり、地球から見て月と太陽の大きさはほぼ同じということ。ここから、太陽の直径と地球から太陽までの距離の比は、月の直径と地球から月までの距離の比に等しいとわかります。太陽の直径を求められるのです。

ちなみに、現在の技術で測定したそれぞれの値は次のようになります。
地球の周長 40,100キロメートル
地球の直径 12,750キロメートル
月の直径 3,480キロメートル
地球から月までの距離 384,000キロメートル
太陽の直径 1,390,000キロメートル
地球から太陽までの距離 150,000,000キロメートル
2.星までの距離を測る。ベッセル
(1)「シリオメートル」の利用。ハーシェル
星までの距離を初めて測定したのは、ドイツの天文学者フリードリヒ・ヴィルヘルム・ベッセルです。けれどこのベッセルの偉業を紹介する前に、もう一人、紹介しなければならない人物がいます。ウィリアム・ハーシェル。彼はドイツ生まれの、イギリスの天文学者です。
ハーシェルの考えた「シリオメートル」について説明します。
ハーシェルの主要な研究は、「星までの地球からの距離を測定する」というものでした。そのために彼は、「明るさは距離の二乗に反比例して減少する」という考えを用いました。これは「星はどれもみな同量の光を出している」という仮定に基づくものです。例えば、明るさが等しい2つの星があるとしましょう。一方が他方の3倍だけ遠くにあれば、遠い方の星の明るさは近いほうの星の明るさの1/9になる、というわけです。見かけの明るさが1/9なら暗い星は明るい星よりも3倍ほど遠くにあると仮定したのです。
シリオメートルというのは、地球から星までの距離の単位です。ハーシェルは、夜空で最も明るい星シリウスを基準として、各星までの距離をシリウスまでの距離の何倍かで呼びました。シリウスまでの距離が1シリオメートル。例えば、明るさがシリウスの1/16の星は、シリウスの4倍遠くにあるのであり、その距離は4シリオメートルとなります。
彼は「すべての星が同じ光を出しているわけではないだろう」とは思っていました。が、いつかシリウスまでの距離がわかったときのための暫定的な距離としてシリオメートルを使っていたのです。
それと、ハーシェルは天の川銀河を予想していました。星は夜空にまんべんなく散らばっているのではなく、隔たりを持って散らばっています。『宇宙創生』には「レーズン入りパンケーキのよう」と書かれています。もしもパンケーキのような平たい空間の中で周りを眺めたなら、レーズンは上下にはあまり見られず、前後左右にたくさん見られるはず。これと同じように、地球から夜空を見上げると、レーズン入りパンケーキの中にいるように星たちが散らばっています。このパンケーキ・天の川銀河を、ハーシェルは直径1,000シリオメートル、厚み100シリオメートルと計測しました。
ただし、ハーシェルは宇宙自体が天の川銀河だと考えていたようです。天の川銀河は、宇宙のすべての星を含んでいると。つまり、彼の頭の中で宇宙は直径が1,000シリオメートルで厚みは100シリオメートルだったのです。
結局、ハーシェルは1シリオメートルがどのくらいの大きさなのか知らずにこの世を去りました。ただ「信じられないほど遠くにある」ことだけがわかっていたと言います。
星までの距離を測り、1シリオメートルの大きさを特定したのがベッセルです。
(2)微小な星の視差を検出。ベッセル
星を観測する天文学者や科学者にとって、長い間、星は謎でした。というのも、星には視差が見られなかったからです。視差とは
二地点での観測地点の位置の違いにより、対象点が見える方向が異なること。または、その角度差
のこと。
物を見るとき、当然ながら、位置が違えば見える方向が違ってきます。右目だけで物を見て、すぐさま今度は左目だけで物を見ると、背景が違って見えます。背景がジャンプして見える。これが視差。見る対象が近ければ近いほど、そして見る位置が違えば違うほどジャンプは大きくなります。
が、星に対して視差は見られないのです。もしも地球が太陽の周りを一年かけて回っているのなら、半年後に見える星の位置はズレて見えるはず。観測点が異なるのですから。それなのに、私たちが星を観測しようとしても視差は認識できない。「もしかして、地球は回っていないのでは……」「不動の地球を太陽が回っているだけなのでは……」。近代以前には、そんな憶測をする科学者もいたと言います。
実際には、地球は太陽の周りを公転していたし、視差も起こっていました。観測対象が、ただただ遠かっただけなのです。「星は信じられないほど遠くにある」から、私たちが視差を観測できないのです。
そんな星に対する視差を一番最初に攻略したのが、フリードリヒ・ベッセルです。彼は白鳥座61番星と呼ばれる星に対して半年かけて観測を行い、1838年に0.0001742度だけ位置を変えていることを確認しました。

ベッセルが検出したこの視差は途方もなく小さい。腕を伸ばして人差し指を立て、左右の目を切り替えて観測したときに視差がこの値になったとすると、腕の長さは30キロメートルあるはずだ。
太陽から冥王星の軌道のあたりまでに含まれるものすべてを、一軒の家ほどに圧縮したと考えていよう。それでもなお一番近い星は、何十キロメートルも離れているのだ。
太陽から地球までの距離はわかっていたことから、ベッセルは観測した角度と三角法でもって白鳥座61番星までの距離も測定しました。ベッセルによると、それは100兆キロメートルとの計算結果。どうでしょう、途方もない数字です。しかも白鳥座61番星というのは、視差を観測しやすい星の1つ。つまり地球からもっとも近い星の1つなのです。
さらには天の川銀河の大きさも見積もれるようになりました。ハーシェルがシリオメートルを使って、星々や天の川銀河の相対距離を計測していたのですから。これにより、天の川銀河のサイズが判明しました。
ここからは単位として「光年」を使います。
1年 31,557,600秒
光の速度 299,792キロメートル/秒
よって
一光年 9,460,000,000,000キロメートル
一光年は約9兆5千億キロ。天の川銀河の直径は約10万光年で、厚みは約1万光年となります。
3.アンドロメダまでの距離を計測。ハッブル
(1)宇宙を計測する物差し。セファイド
さらなる巨大数を計測したのはエドウィン・ハッブルです。彼は1923年に、アンドロメダ銀河までの距離を測定しました。彼はアンドロメダ銀河内にセファイドを観測し、それによりセファイドを含むアンドロメダ銀河までの距離を求めました。当時、セファイドは星までの距離を測る基準になっていたのです。ではセファイドとは何か。
セファイドとは、明るさが変化する変光星の一種です。星の明るさが変化して見える原因はいくつかあります。例えば連星と呼ばれる星があり、ペルセウス座のアルゴルがこれに当たります。2つの星がお互いの周りを回っている。故に、暗い方の星と明るい方の星、どちらが手前に来るかで、地球から見た場合の明るさが変化します。それから爆発型変光星と呼ばれるものもあり、これは外層や周囲の大気が爆発することで明るさが変化する星とのこと。
これらに対してセファイドとは、脈動変光星のことを言います。脈動変光星は、膨張と収縮を繰り返すことで明るさが変化します。
たいていの星は安定した平衡状態にある。ここで「安定した並行状態にある」というのは、おおよそ次のようなことだ。星は大きな質量をもつため、重力の作用で潰れようとするが星が潰れれば内部の物質が圧縮されて温度が上がり、外向きの圧力が生じる。これら二つの作用が釣り合って、星は安定した状態にあるのだ。
(中略)
しかしセファイドは安定した平衡状態にはなく、状態が揺れ動く。セファイドの温度が比較的下がっているときには、星は重力に抗しきれずに収縮する。星が収縮すると内部の物質は圧縮されて、中心部でのエネルギー生産を促し、新たに生じたエネルギーのために温度が上がり、星は膨張する。膨張しているあいだはエネルギーが放出されるため、温度が下がって星は収縮に転じる。このプロセスがいつまでも続くのだ。ここで重要なのは、収縮すると星の外側の層が圧縮されて透明度が落ち、その結果としてセファイドの暗い時期が生じることである。
セファイドが星までの距離を測る基準になるのは、「星の実際の明るさと見かけの明るさは異なる」にも関わらず「セファイドは変光周期が同じであれば、実際の明るさもおおよそ同じである」からです。
星が実際に放っている光の強さと、それを地球で観測したときの明るさは異なります。この実際と見かけの光度の齟齬は、地球からの距離を曖昧にしてしまうので厄介なのです。見かけは明るくとも、実際には近くにあるだけの暗い星かもしれないし、反対に見かけは暗くとも、実際には遠くにある明るい星なのかもしれない。
これを解決したのが、セファイドの変光周期と明るさの関係です。簡単に言えば、セファイドの光度が大きいほど、変光周期は長くなります。周期の等しい2つのセファイドがあるとしたら、たとえ見かけの光度が違っていても、それら2つのセファイドはおおよそ同じ明るさで輝いていることになります。これを発見したのは、アメリカのリーヴィットという天文学者。彼女は1922年、小マゼラン星雲内にある25個のセファイドを見つけ、これらの変光周期と明るさの関係を見つけました。彼女は、これら25個のセファイドは地球からほぼ等距離にあると考えました。地球から小マゼラン星雲までの距離はわかりませんでしたが、同じ星雲内にあるということは、互いに近くにあるのだろうと考えたのです。
私たちは星を見る時、星の実際の光度自体は認識できません。けれど、セファイドの「同じ変光周期であれば明るさは同じ」という法則に見かけの明るさをプラスして計算すれば、セファイドまでの距離を特定できます。周期の等しい2つのセファイドがあって、一方の明るさが他方の九分の一だったなら、その暗い方のセファイドは、明るい方のセファイドよりも3倍の距離の位置にあるのです。
このセファイドの法則によって、セファイドまでの相対距離を示すことができるようになりました。「こっちのセファイドは、向こうのセファイドよりも◯倍遠くにある」という風に。そして後年、他の天文学者によって、セファイドまでの絶対距離も判明することになります。視差などをつかって、ある特定のセファイドまでの距離が測定されたのです。こうしてセファイドは変光周期によってその距離をつかめることがわかり、距離を測る際の基準になりました。ある星までの距離を測りたい時、近くにセファイドがあれば、その星までのおおよその距離もつかめたのです。
(2)アンドロメダのセファイド
1920年代、天文学の世界では、ある一つの論争で湧いていました。それは、星雲は天の川銀河の内部にあるのか、それとも天の川銀河の外にある別個の星の集団なのか。ハーシェルが天の川銀河の大きさ(宇宙の大きさ)を測定しましたが、限界を示されると「その向こう側は……」と考えざるを得ないのが人間です。「星雲」と呼ばれる夜空のシミのようなものは、徐々に星の集団だとか考えられるようになり、果たして星雲はどの程度の距離にあるのか、論争の的になりました。もしも星雲が天の川銀河の内部にあるのなら、「天の川銀河は宇宙そのものだ」という説は有力となります。反対に、星雲が天の川銀河の外にあるのなら、宇宙は天の川銀河の外にも広がっていることになります。
1923年、ハッブルはアンドロメダ星雲を観測中にセファイドを見つけます。つまり、このセファイドを使ってアンドロメダ星雲の地球からの距離を求められるようになったのです。アンドロメダ星雲内のセファイド。果たしてこのセファイドは、天の川銀河の内部にあるのでしょうか。それとも、それよりも遥か遠くにあるのでしょうか。セファイドまでの距離を測定したところ、90万光年先にあることが判明します。天の川銀河の直径はたかだか10万光年だから、セファイドを含むアンドロメダ星雲は、天の川銀河とは別個の星の集団だということになります。それまで星雲と呼ばれていたアンドロメダは、これよりアンドロメダ銀河と呼ばれました。
4.まとめ
このように、宇宙は途方もない巨大な数で溢れています。アンドロメダ銀河は、現在では地球から約200万光年先にあると算定されており、その直径も約22万光年、含まれる恒星は約1兆個です。が、巨大なアンドロメダ銀河ですら、宇宙のごく一部でしかありません。宇宙はただただ破格。アンドロメダ銀河に1兆個の恒星が含まれると言っても、恒星と恒星との間には、広大な星間空間が広がっているのですから。
ハッブルは自分の観測結果を使って、恒星や惑星に含まれる物質を宇宙全体に均一に広げたとすれば、宇宙の平均密度はどれぐらいになるかを計算してみた。結果は、地球千個分の体積にわずか一グラムというものだった。(中略)宇宙の大部分はからっぽの空間だということを意味している。
惑星も恒星も銀河も、典型的な存在ではありえない。なぜなら宇宙は、ほとんどなにもない空間だからだ。典型的だと言える場所があるとすれば、それは果てしなく広がる冷たい真空の中の、永遠に終わらない夜の闇に沈む星間空間だけである。
なので、たかだか千年を「永遠」などと言っていられないのです。それ以上速く進むものがない光ですら、天の川銀河を抜けるのに10万年かかるし、アンドロメダ銀河に到達するには200万年かかります。小規模な千年どころで騒いでいられません。
さらには、「永遠」は巨大数とはまた別の話でもあります。いくら巨大な数を積み重ねたとしても、永遠には届かないのですから。10万光年も、22万光年も、200万光年も、たとえそれらが何億回と繰り返されようと、永遠にとってはただの始まり過ぎません。
産屋敷輝哉の「千年は永遠である」は、正しいとは言えないことがわかっていただけたでしょうか。ただ、だからといって「人の思いは永遠である」までが間違っているのかどうかまではわかりません。根拠の一つを崩したに過ぎず、「人の思いは永遠である」だけの別の根拠があるかもしれませんから。私に言えるのは、お館様の主張の前提の1つが間違っている、ということだけです。
参考
中世における宇宙論をめぐる攻防のところが、とくに面白かったです。この時代は主張を通すのも命がけなので。すぐに投獄されたり火炙りにされたり。実際に火炙りにされたのは、イタリアの哲学者・修道士ジョルダーノ・ブルーノ。彼は著書の中で、「宇宙は無限であり、星星はそれぞれ惑星を持ち、各惑星上には生命が存在する」と論じたとか。いや、さすがに聖書全盛の時代にそこまで言ったら、教会から目をつけられることが予想されましょう。案の定、彼は衣服を剥ぎ取られ、猿ぐつわを噛まされ、杭に縛られて焼かれました。死刑判決を受けた時のブルーノの言葉が、彼の胆力と悲壮を想起させます。
おそらくは私に判決を下したあなたがたのほうが、判決を受けた私よりも大きな恐怖を感じているのだろう
で、この時代の趨勢を漫画にしたのが『チ。ー地球の運動についてー』です。
漫画による表現というのは素晴らしいですね。絵とストーリーで感情が刺激されて、『宇宙創生』などの本を読んだときとはまた違う感動があります。ラファウの言動が頼もしくて、また悲しくて。フベルトから教えられた地動説のシンプルな美しさに目覚めたときや、腹をくくってノヴァクに「畢竟、それは知性だ」と言い放ったときなど。合理性をモットーに生きていた彼が、それまでのモットー(と命)を捨ててでも美を取ることに目覚めたというのが……それほどの覚悟を決めた彼の判断というのを羨ましく思います。
今度の10月からはアニメ放送されるようで。動画であれば音声や動きも加わって、また別の表現による感情の刺激があるのでしょう。
この記事が気に入ったらサポートをしてみませんか?
