転位から塑性理論を理解すること -2-

多結晶構造を前提とした金属材料の塑性変形（結晶塑性）に必要不可欠な存在と言える「転位」について。いわゆる「線欠陥」に分類されますが、原子空孔や不純物原子のように実体的な欠陥ではなく、原子配列の局所的な乱れとして扱われます。

出典：九州工学教育協会（弱い鉄から強い鋼に-自在に強さを変える!），http://qsee.jp/switch

今回は「転位」について、物理現象（変形問題）と関連付けながら、どのような振る舞いがあるのかを見ていければと思います。

前回は初回でしたので、転位に関する物理的な見方について、複数の視点から整理してみました。

今回は転位の弾性論（材料力学では「弾性領域」に相当する分野）を中心に、力学的な観点から話を進めていきます。

直線らせん転位が作る弾性場

ここでは線形等方弾性論を用いて、転位の周囲の弾性場（ひずみ場と応力場）を可能な限り手計算で導いてみます。加えて、弾性ひずみエネルギーに関して見ていければと思います。

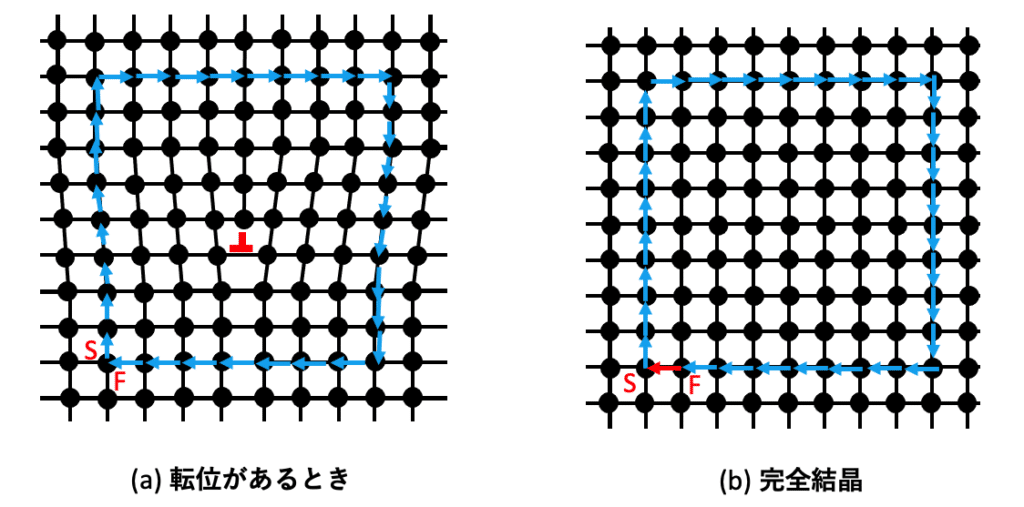
直交座標系において、無限大の物体中に１方向に無限に長い直線状のらせん転位を考えます（図面は上下方向を無限長と見做します）。

おこで、らせん転位は転位線（物体上の破断の切れ目）と転位のバーガースベクトルが平行である場合に相当します。まずは、物体の上下方向に対する断面上の任意の点の変位を出します。

ここで、以前の連続体力学の話で登場した「変形勾配テンソル」の対称成分を、転位論における「ひずみ」として扱います。

$${\varepsilon_{ij}=\frac{1}{2}(\frac{\partial{u_i}}{\partial{x_j}}+\frac{\partial{u_j}}{\partial{x_i}})}$$

このらせん転位（モデル）における変位の情報は上下方向の成分だけ。表記をｅに変えていますが、弾性ひずみとしては、非対角成分に相当する４成分が計算されます。

等方弾性体においては、独立した弾性定数は主に２種類（ラーメ定数）に集約されます。一部の成分を例示すると、下記の通りです。

• $${\sigma_{11}=\lambda(e_{11}+e_{22}+e_{33})+2{\mu}e_{11}}$$

• $${\sigma_{12}=2{\mu}e_{12}}$$ , $${\sigma_{13}=2{\mu}e_{13}}$$

転位（線欠陥）の線上において距離（ｒ）に変数を集約すると、ひずみ場と応力場は上記のように求められます。弾性ひずみエネルギーは変数（ｒ）を無限化した広義積分から求められます。

直線刃状転位が作る弾性場

刃状転位はらせん転位とは異なり、転位線と転位のバーガースベクトルが垂直です。変位成分は前回の類推から下記のように求められます。

$${u_1=\frac{b}{2\pi}tan^{-1}(\frac{x_2}{x_1})}$$

ところが、この変位成分は変位場に対する適合条件を満たしません。詳細は転位の運動方程式を見ることになります。これは、刃状転位の変位成分が連続的な変化にならないためです。

$${m\frac{\partial^2{u_i}}{\partial{t^2}}=(\lambda+\mu)\frac{\partial^2{u_j}}{\partial{x_i}\partial{x_j}}+{\mu}\frac{\partial^2{u_i}}{\partial{x_j}\partial{x_j}}}$$

計算過程は今回は省略します。らせん転位の場合に比べて複雑な計算処理を使うためです（デルタ関数を部分的に使用します）。

刃状転位が作る応力場は、対角成分と非対角成分の両方ともに値が存在します。また、刃状転位は応力場の対角成分の和（トレース）が値として存在します。らせん転位は対角成分（静水圧相当）が存在しないため、トレースはゼロになります。

応力場における静水圧成分の有無については、らせん転位と刃状転位の違いのひとつです。

転位に起因する弾性ひずみエネルギー

らせん転位と刃状転位の双方に言える話として、ひずみ場と応力場は距離（ｒ）がゼロの極限を取ると発散することが挙げられます。

線形弾性論に基づく説明を付けるならば、弾性ひずみ（数値）は１に比べて小さいため、距離（ｒ）が微小値である場合は適用外と言えます。

つまり、物体の形状は中空状態と見做され、中空領域（ｒが微小値である場合）は「転位の芯」と呼ばれる存在として扱われます。

ひずみエネルギーは転位の芯に関する設定次第ではありますが、距離（定数）の比に関する対数関数として求められます。

らせん転位に関して、銅の材料定数を適用してひずみエネルギーを算出すると、原子空孔の形成エネルギーに比べて大きいことが分かります。

これは物体が平衡状態において、転位が実体として存在しにくいことを示唆しています。

おわりに

今回は等方弾性論を前提として、転位の力学的な位置付けを見てみました。らせん転位については手計算で扱える範囲でしたので、ある程度ですが、導出過程も記しています。

次回は転位に働く力について、そこから転位の増殖過程にまで話を進められたらと思います。

-------------------------
最後まで読んで頂き、ありがとうございます。この記事があなたの人生の新たな気づきになれたら幸いです。今後とも宜しくお願いいたします♪♪
-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎