
物理数学の世界 #10 〜剛体の力学(1)〜
#本記事は2021/8/10の記事を書き直したものです。
物理数学の世界。始まります!
前回は行列の固有値問題と対角化を扱いました。ここ数日は、線型代数をテーマに取り上げていました。
今回は物理学の話に戻りまして、剛体の力学問題を扱います。以前に質点の力学問題を扱いましたが、質点に比べてより現実的な挙動を見渡せる代わりに、数学的な処理などのレベル(難易度)は上がります。
今回は基本事項を整理するだけでノート(1ページ)が埋まりました。実用的な話は次回に引き継ぐとして、まずは今回の内容を着実に理解していただければ良いとと思います。
![]()
整理したノートを公開
実際にノートにまとめてみました。まず、質点と剛体の違いについて。質点は質量だけを有するのに対して、剛体は質量と大きさ(形状)を有します。
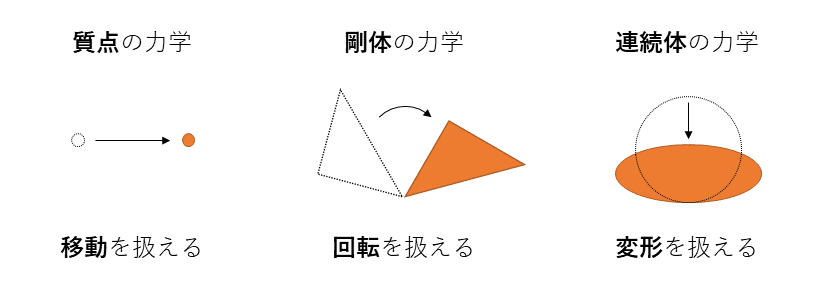
この分類に従うことで、物体の運動で扱える範囲が決まります。剛体は並進運動と回転運動を扱います(変形については扱いません)。

剛体は形状をもつため、物体の挙動を求める際には重心の特定が必要不可欠になります。重心を知ることで、数学的な処理を簡潔に行うことができます。
そして、今回で新たに登場するのが慣性モーメント。並進運動の運動方程式での質量(M)に対応します。慣性モーメントは回転のしにくさを表すもので、形状と回転軸により決まります。
この辺は物理定数のような存在なので、剛体運動を扱うような参考書を参照するのも手です(下記のサイトに代表的な形状の慣性モーメントが載っています)。
参考までに見ていただけたらと思います。
![]()
質点と剛体と変形体
今回までに質点と剛体の2種類を扱いました。変形体についても今後の機会で書く予定です。ところで、どうして物体の扱い方として、質点や剛体が存在するのでしょうか。
基本的に最も現実的なのは、物体を連続体として扱うことです(連続体は剛体運動に加えて変形も扱う)。ただし、この変形を手計算で解こうとするのは、計算量が多いので現実的ではありません。
そんな時に扱い方を簡略化するために存在するのが、質点や剛体です。いずれも変形しないという前提を置くことで、手計算でも解けるような問題に落とし込むことができます。
つまり、いきなり連続体として計算量の多い問題に取り組むより、質点や剛体で簡単にした問題に取り組むほうが、出戻りも少なくて確実です。
特に、工学のレベルでは、ある程度満足する答えが得られるのなら、問題を簡単化した方が良いと考えることが多いです(ケースバイケースですが)。
![]()
おわりに
今回は剛体の力学問題を扱いました。質点に比べて考慮することが多くなるので、少し複雑な感じたりもしたと思います。
内容的には大学レベルの問題です。参考書としては、物理学の他に機械力学の参考書も有効だと思います(自分はこの辺の教科書で学習しました)。
剛体運動を扱うことは、機械設計などでも必須の考え方ですので、ここできちんと理解して進んでもらえたらと思います。
-------------------------
最後まで読んでいただき、ありがとうございました。実際は非定期ですが、毎日更新する気持ちで取り組んでいます。あなたの人生の新たな1ページに添えるように頑張ります。何卒よろしくお願いいたします。
-------------------------
⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎
⭐︎⭐︎⭐︎ ブログのロードマップ ⭐︎⭐︎⭐︎
