解析学の基礎である微積分の話 -4-

前回に引き続き「解析学」をテーマに書きます。解析学は数学を構成する大きな分野のひとつで、高校数学で学習する「微積分」を本格的に紐解いたものです。

前回は解析学の本場とも言える「微分方程式」について取り上げました。

今回も微分方程式を扱いますが、少しレベルの高い内容を紹介します。より物理に則した問題を取り上げて、その挙動を微分方程式を解くことで理解します。

テーマは「１自由度の減衰自由振動モデル」と呼ばれる力学の問題です。複雑な数式展開もあるので注意しながら見ていきます。

減衰自由振動の力学モデル

現実の機械振動という物理現象を単純化する手段のひとつとして、質量（マス）とバネとダンパの３要素で構成された「減衰自由振動モデル」があります。

１自由度の減衰自由振動モデルを示します。非減衰振動はバネの要素によるもので、変位に比例した力を発生させます。また、減衰の効果はダンパと呼ばれる要素で表現され、速度に比例した力を発生させます。

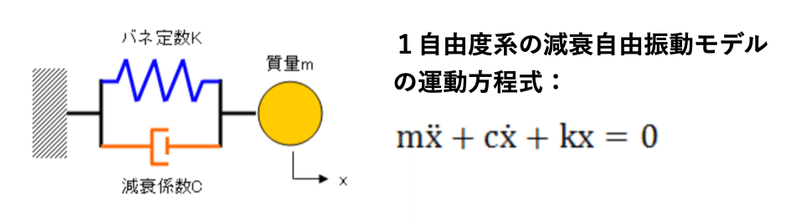
変位（x）の上に２つのドッドが付いていますが、これは変位（x）を時間（t）で２回微分することを表しています。ドッドが１つなら変位（x）の１回微分です。

変位（x）の２回微分は加速度を表します。運動方程式の第１項は質量と加速度の積（慣性力）を表現しています。第２項はバネにより発生する復元力、第３項はダンパにより発生する減衰力です。

減衰自由振動を解析的に求める

運動方程式から一般解を求めてみます。定数（γ）と定数（ω）はそれぞれ減衰と単振動の周期（周波数）を意味する物理条件です。

今回扱う微分方程式は、「２階斉次線形微分方程式」と呼ばれています。２回の微分形があること、右辺がゼロであることに由来します。物理的には外力（マスに働く強制力）を解放したときに相当します。

一般的な減衰振動は「0<γ<ω」の関係が成立するときに発生します。この条件を外すと振動が全く発生せず減衰する「過減衰」や、減衰がほぼ発生せず永続的に振動し続ける「単振動」の挙動を示します。

物理条件「0<γ<ω」が成立するとき、変位（x）は下記のグラフのようになります。一般解である変位（x）の式を見て頂ければ分かる通り、減衰と振動で表現される部分が分けられています。

先ほど示した変位（x）のグラフ（時刻歴）を実際に求めるには、初期条件を決める必要があります。そこから積分定数を求めます。

バネ定数や減衰係数は物理的なパラメータであり、その兼ね合いで振動する挙動が異なるところは、物理ならではの面白さだと思います。

おわりに

今回は「１自由度の減衰自由振動モデル」を説明することで、微分方程式の現実的な使い道に触れました。

実際に計算をする過程で、減衰自由振動の場合は最初に求めた定数（λ）が複素数である必要があります（今回はその辺の詳細な計算は省略しました）。

厳密に言うと定数（λ）の実部が減衰の特性、虚部が単振動の特性を表します。

詳細な計算過程に興味がある方は、上記を参考に実際に計算を進めて頂くと良いと思います。

-------------------------
最後まで読んで頂き、ありがとうございます。この記事があなたの人生の新たな気づきになれたら幸いです。今後とも宜しくお願いいたします♪♪
-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎