微分積分と物理学の関係性に触れる 〜解析学について〜
数学という学問の始まりはいつか?
実は「数学」は今から30万年ほど前から存在していました。その時代はどのような数学が存在していたかと言うと、たし算・ひき算はおろか、数を数えることよりも簡単なことが行われていたそうです。
そこから長い時間を経て、徐々に学問として形作られてきた数学ですが、それは沢山の偉人たちが作り上げてきた歴史でもあります。

今回は数々の偉人たちが作り上げてきた「数学」について、現代の視点から迫りたいと思います。数学の分野は伝統的に解析学・代数学・幾何学と呼ばれる3つの分類があります。これが最も大まかな分類です。
初回は「解析学」から見ていきたいと思います。

解析学とは
解析学は高校(理系方面)で学習する「微分積分」を更に発展させたもの。極限操作を含む演算を主要な道具とする点が大きな特徴です。
例えば、物事の変化を「微分方程式」で記述し、その解の性質を調べるということは、ニュートン以来の数学の重要な考え方と言えます。
解析学については、先ほどの「微分方程式」の他に「確率論」や「複素解析」など様々な側面を持ち合わせています。微分方程式は工学系の方面で登場する「力学」を説明する上で基礎的な存在です。

微分方程式の使用例
微分方程式を使うことで、力学的な変化を調べることができます。その簡単な例題を示します。雨粒を質点と仮定した場合の自由落下について、運動方程式(微分方程式)の解を求めることから考察します。

特殊解に対して時刻tの極限を取ると、定数値に落ち着きます。つまり、雨粒が地上付近に到達する頃には、雨粒の落下は等速直線運動に落ち着きます。これは、雨粒が空気中の粘性抵抗を受けるためと考えられます。
仮に粘性抵抗(粘性係数:c)を無視した場合、どんどん速度が上がるような自由落下です。これでは、雨粒を受ける私たちへの衝撃は途轍もないことになると想像できますが、実際はそんなことは起こりません。
このように、物理現象を詳しく考えるには、微分方程式を解く作業が必要不可欠であることが分かります。
より現実的な物理現象を対象とする場合は、微分方程式も複雑な形になるので、手計算で解くことは困難になります。その場合は、コンピューターを利用した数値解析から解を求めたりします。

ナビエ・ストークス方程式
ナビエ・ストークス方程式は流体力学で登場する流れに関する方程式です。流体の性質として、一般的に圧縮性と非圧縮性の2種類があり、非圧縮性は圧縮性の特殊な場合として考えます。
物理現象として流れを解く場合は、大抵は非圧縮性を仮定して問題を扱います。また、先ほど説明した数値解析を利用するとも多いです。このような解のことを、数値解(弱解)と言います。
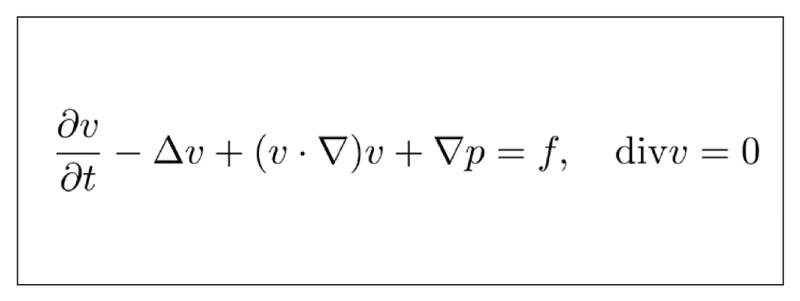
非圧縮性のナビエ・ストークス方程式の厳密解(強解と言います)は、クレイ数学研究所の懸賞問題にもなるほど難しい問題です。まさに、数学専攻の領域に相応しい問題と言えます。

おわりに
今回は数学の領域から「解析学」について見ていきました。解析学は工学の分野でも大活躍するほど重要な分野です。
私も数学の中では、解析学にお世話になりました。前にお話しした「有限要素法」に関しても、今回の解析学が土台になっています。
これからも学んでいく必要のある分野だと思います。同時に面白さも発見できるかもしれません。
次回は代数学についてお話しします。
-------------------------
最後まで読んでいただき、ありがとうございます。実際は非定期ですが、毎日更新する気持ちで取り組んでいます。あなたの人生の新たな1ページに寄り添えたら幸いです。何卒よろしくお願いいたします。
-------------------------
⭐︎⭐︎⭐︎ プロフィール ⭐︎⭐︎⭐︎
⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎
この記事が気に入ったらサポートをしてみませんか?
