
シャニマスと学ぶ確率・統計【算数〜大学教養統計】(スプシも少し)
追記・修正記録
8/15 平均、分散、標準偏差の項の分散に対する説明
イントロ
青のりと申します。
無駄話(読まなくていい)
突然ですが質問です。現在の魑魅魍魎としたソシャゲ界隈の中で、「シャニマス」というゲームはどのような特徴を持っているでしょうか。
コミュの文学性や表現の鮮烈さ?
幅広い音楽性?
各登場人物の実在性?
イラストの大胆さ?
グレフェスや育成ゲーとしてのゲーム性?
WINGマスター?
大吉 or LATE?
こんなものただの主観でしかないので各人にそれぞれの答えがあると思いますが、今回取り上げたいのはこれです。




すなわち「教育」です。
特に今年に入ってからの勢いは最早『スゴ味』すら感じます。
(正直何を経てそんな方針になったのかはめちゃくちゃ気になりますが、シャニマス1ねんせいは「何かを始めるのに遅過ぎるなんてことはない」というメッセージと「香川さんも1ねんせい」という構図、そしてパロディのシュールさなどなどしっかり考えられている感じがありますし、「〇〇の日」は単純接触効果とかコミュを読むきっかけとして良いと思いますし、283体操も童心に帰ることと「セツナ」というテーマとの合致、そしてオタクの生活習慣をなんとかしようというコンセプトとして納得できますし、かるたは大喜利がtkym氏の性癖であると考えると自然かなと思います。)
また、シャニマスのコミュは元ネタが明らかなものがしばしばあり、元ネタを知らなかった人がそういった作品に触れる良い機会にもなっています。別に知らなくても普通に面白いのですが、元ネタを知るとニヤリとなったり、話の奥行きが増すことがよくあります。今これを書いている時間は本来『白鯨』を読む時間に充てるつもりでした。(好きでやってることです。)
要するに、シャニマスは学ぶ場でもあるということです。(勿論楽しみ方の一つに過ぎませんが)
それに乗じて「私がシャニマスをプレイする上で使う確率や統計の知識」について書いたのが今回のnoteです。要は布教。
前置き(こっちは読んで欲しい)
シャニマスというゲームのプレイスタイルには色んなものがありますが、その一つに「未発見の法則や未解明の数値を統計により分析する」というものがあります。響きはなんかかっこいいですが、ポチポチカウントするのが実際の作業のほとんどです。ゲーム人口がそんなに多くない関係で、やる気と少しの時間さえあれば誰でも最前線に立てるのがこのプレイスタイルの良い所だと思っています。
ただ勿論、「こんな結果になったよ〜」だけでは話が進まないので、「こんな結果になったから解析するとこんな感じだと推定できたよ〜」と数学や統計学を使って分析を行うのですが、その時に検定やら有意水準やらp値やら、学んだことのない方からすると「ほ〜〜ん」となるだけの用語が頻出します。
それについて、少しでも分かっていただけるように解説するのがこの記事、という訳です。
今回書く動機、目的としては次の2つが主としてあります。
①集計、統計してくれる人を1人でも増やすこと
②やっていることが別に難しいことではないと思ってもらうこと
①はそのままで、「シャニマスで何か集計をして自己満足なり周囲に貢献なりをしたい」という方に必要かつ最小限の知識や考え方を解説する、ということです。主目的。
あとこういう方を増やして自分がガバ理論を構築した時に指摘してもらいたい。
②について、私はちょくちょくシャニマスについて何かしらを集計して、結果をTwitterやnote上でそれを発信したりしなかったりしているのですが、そのツイートに対する反応を見ていると、「なんか難しい統計の話」みたいな認識をされることが多いようです。
ただ私は別にそんな難しいことをやっている訳ではなく、高校数学に少し知識を足したことをしているだけ、というのを分かってもらいたいのです。
それで①が少しでも達成できたら良いですし、そうでなくてもそういった人たちが最低限どんなことをやっているかのお気持ちだけでも理解していただければ私の目標は十二分に達成できたことになります。
一つ断っておきたいのですが、私は統計の専門では全くありません。今時自然科学に関わる人間であれば最低限の統計やAIについて学ぶことはあると思うのですが、私はそれに少し毛が生えてるか生えてないか、つまりほぼハゲくらいの人間です。
それに関して、今回記事を書くに当たり資料や教科書を読み直したり新しく読み漁ったりしたので専門外を免罪符にするつもりはないですが、どこかしら間違えてる可能性は普通に高いのでもし間違ってる箇所があれば遠慮なくご指摘ください。崇め奉ります。
・そもそもこの手の話はある程度普遍的なものなので、きちんと勉強したいのであったら市販されてる教科書を買ったり解説動画・記事を見た方が全然良いと思います。あくまでこのnoteは「シャニマスという身近な題材の中で、数学や統計の知識がどのようなもので、どのように使われるか?」を解説するものだと思ってください。また逐一証明などすると文量が本当にとんでもないことになるので、計算する上で知っておくと良いことを掻い摘まんでいます。お気持ちお気持ち。
・多分これを読んで集計をしてくださる大半の方はexcelやスプシを使って集計すると思うのでスプシでの計算方法とかも載せてます。(一人でやるならexcelの方が機能に優れていますが、macだと不便なのと、自分で買うと高い。スプシは無料かつ共有しやすい。ただ「excelやスプシ」と一々書くと冗長なので全部ただexcelって書いてます。)
が、扱うデータ量が増えたり、多少複雑なことをやろうとすると表計算ソフトは不便なことが多いので、もしそうなったらR(統計用の言語)とか使えるようになった方が多分楽です。無料ですしかなり簡単です。多分最難関は環境構築。
説明に所々グラフを描画したりもしてますがそれはgnuplotを使ってます。手軽なのがグー。
・最大限短くなるよう努力しましたが、テーマがテーマだけに結構な長さのnoteになってしまったので、文科省の学習指導要領を基に、使う知識を学校ごとにレベル分けしました(説明の都合で一部ズラしたりもしています)。
読み飛ばす際の参考にどうぞ。
というかこのnoteは頭から最後まで読むものというよりは、「よく分かってないけど分かりたい部分」だけ読む用に作ってます。勿論全部読んでもらえることが嬉しいことには違いないですが…
説明の都合とかあんまり使わないだろうと思ってカットした知識とかも結構あるので、「この部分解説して欲しい/参考文献欲しいんですけど!!!」って思ったらコメントにでも書いてくださると喜びの舞を踊りながら追記します。
算数、中学数学
調べた感じ内容にそこまで差が無かったのでまとめました。あさかほ…

知識
・試行と事象
・確率
・余事象
応用
・ガシャを天井する確率
試行と事象
これは確率の計算や理論というよりはこれから使う用語の説明です。確率等について解説する時にはよく使われる単語です。
「試行」とは、コインやダイスを振る、ガシャを引くといった、「(同じ状態で)確率的な結果を生み出す行為」だと思ってもらえれば良いです。
「事象」とは、試行に対する結果です。「コインを投げて表が出る」「さいころを振って奇数が出る」「ガシャを1回引いてSSRを引く」などは全て事象です。
確率
確率というのは、「1つの試行においてある事象が期待される割合」です。
記号として、事象Aが起こる確率をP(A)と書きます。
あと「事象A、Bが両方起こる確率」,「事象A、Bのうち少なくとも片方起こる確率」をそれぞれP(A∩B),P(A∪B)と書きます。
確率の一つの求め方として、「同様に確からしい根元事象」(さいころで3の目が出ること、コインで表が出ることみたいな一番細かい結果だと思ってください。さいころで3の倍数の目が出ることだと、3の目と6の目に分割できるので当てはまらない)について、(その事象の場合の数)/(全ての事象の場合の数)で与えられる…という風に習ったと思います。
ただぶっちゃけこれはかなり簡単な場合のみにしか適用できず、シャニマスにおいて適用できるのは札回しがギリギリくらいだと思います。実際の所、そもそも「同様に確からしい根元事象がある」という状況がそんなにある訳では無いですし、現実問題、100通りとか1000通りとか数え上げるなんて手間がかかりすぎます。
ガシャとかドロップ率など、そもそも元の確率が決まってて、そこから色々な確率を計算する、という場合が殆どです。
余事象
「Aが起こる確率を知りたいけど、それを計算によって求めるのは難しい…でもAが起こらない確率なら求められる!」という時には、1から〈Aが起こらない確率〉を引けば良い訳です。この「Aが起こらないこと」をAの余事象と言います。
例としては「〇〇回ガシャを引いて△枚以上当たりを引く確率」を求める時があります。例えば「100連ガシャで0.5%の限定sSSRを1枚以上当てる確率」を求める場合、「1枚以上」というのは1、2、3、…100枚を指すわけですが、そんなわざわざ100パターンも計算してられないので、0枚の場合のみを考える、というわけです。(この例だと実際には沢山出る確率なんてほぼ0なので、1~5枚あたりを計算すれば実用上問題ないですが。)
一応この知識だけでも上の確率は(常識的な発想で)計算できますが、一応後の単元を説明するまで待っておきます。
高校数学

知識
・順列
・階乗
・組み合わせ
・二項係数
・条件付き確率
・独立性
・反復試行
・母集団と標本調査
・平均と不偏分散と標準偏差
・期待値
・ネイピア数
学習指導要領が改訂され、2007年4月1日以前2006年4月2日以降(訂正。時間逆行してました)に生まれた世代(2022年度の高1以下)は数Bで標本調査とか区間推定とかやるらしいですね。ジェネレーションギャップ怖い。
応用
・パッシブの埋まる確率
・ガシャ確率全般
・アビリティ取得数とノウハウ発現率の関係
・1%で当たるガシャを100回引いた時、1回以上当たる確率は?(2秒で答えて)
順列と階乗
これ自体が明示的に使われる状況はそんなにあるわけではないのですが、「場合の数」(≒パターン数)を計算する時の基本となるので解説します。
いくつかのものを、順序をつけて1列に並べる配列を順列と言います。
より詳しくは具体例で示した方が早いと思うのですが、
「a,b,c,dの4文字のうち、異なる2文字を使って並べる場合の数」や、シャニマスで言えば「デュエットを伴わない5人ユニットが5T目に思い出linkを撃つ場合、4T目までの札切りは何通り有り得るか」といった感じですね。
前者については、
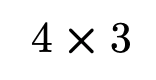
後者については、各アイドルに2種類のLSがあるので、

これを一般化し、「異なるn個のものからr個選んで並べる場合の数」を表したのがこの記号です。

ここで、特に「異なるn個のものを(全て)並べる場合の数」を階乗という概念で表します。これは1からその数までの自然数の積となっています。

組み合わせと二項係数
重要。
前項では「異なるn個のものからr個選んで並べる場合の数」を考えましたが、これを並べず、「異なるn個のものからr個選ぶ場合の数」としたのが組み合わせです。nCrと書きます。
ここで1つの組み合わせに対し、順列はrの階乗個存在するはずなので、次の等式が成り立ちます。

この係数を「二項係数」と呼んだりもしますが、名前の由来については割愛します。そういうものだと思ってください。詳しくはこちら。
参考:二項定理の意味と係数を求める例題・2通りの証明 - 学びTimes
二項係数はexcelだとnCrはCOMBIN(n,r)で計算できます。
条件付き確率
もしかすると高校で習った時、「よく分からない」となったかもしれない条件付き確率についてですが、これは概念自体はそう難しいものではありません。
例えばpSSR率が2%、限定pSSR率が0.5%のシャニマスのガシャにおいて、「1回のガシャで限定pSSRが出る確率」は0.5%ですが、「1回のガシャにおいて、演出がpの虹カーテンだった時にそれが限定pSSRである確率」は、カーテン2%のうちの0.5%、つまり0.5/2=1/4=25%ということになります。これが「演出がpの虹カーテンだった時に限定pSSRを引く条件付き確率」です。同時に、「長めの読み込みが入った時にあなたががっかりする条件付き確率」は75%と言えるかもしれません。
要は、フツーの確率は「1回の試行(⇒全ての事象)に対して期待できる割合」を指しますが、条件付き確率は「ある事象に対して期待できる割合」のことです。
言葉を足すと、事象Aが起こったときに事象Bが起こる確率を「事象Aが起こったとき事象Bが起こる条件付き確率」といい、このように表します。

両辺にP(A)をかけると、「事象A、Bが両方起こる確率」はこのように表すことが出来ます。

この式は当たり前といえば当たり前で、例えば「LP1周で思い出++lv5が落ちる確率」を求めたくば、LPで思い出5になる割合(仮に75%とします)と、思い出5になった場合に思い出++lv5がドロップする条件付き確率(仮に0.25%とします)とを乗じます。

ここで1点注意ですが、上で挙げたカーテン演出とpSSRの例や思い出5と思い出++lv5の例は、時系列的に「過去にある事象が起こったとき、未来にある事象が起こる条件付き確率」となっています(これを時間順行と言います)。こちらは上の計算式を使わずに自明に分かっていることが多いです。
一方統計などではその逆、「未来である事象が起こったとき、過去にある事象が起こっていた条件付き確率」を求めたいことがよくあります(時間逆行)。上の計算式はそういった時に使われます。
例えば、「現在のグレ7のブラバ頻度に対して、VoアルストとViシーズの脅威度」という問題があったとします。
ここから個人的感想と問題設定に都合の良い妄想を基に単純化していきます。この部分に対する苦情は受け付けません。
単純化して、ViシーズとVoアルストのどちらか1つのみとマッチングし、他の対面は全て無害なコイキングにしましょう。
Voアルストは火力がやべーです。1T目からのバフ量とサマハニ。
Viシーズも思い出linkCONTRAILLATE夜会とやべーですが、タイプ不一致の大吉を撃つこともそれなりにあり、かつ環境にVi編成が多いのでViを最初から抑えることも多いです。
ということで、Voアルストが対面にいる時にブラバさせる確率を50%、Viシーズがブラバさせる確率を30%とします。これだけだとVoアルストの方がやべーですね。
ですが今問題にしているのはブラバの頻度そのものです。Voアルストの数が圧倒的に少ないなら、ブラバの頻度にはそこまで影響しないことになります。例えばVoアルストとのマッチングは30%、Viシーズとのマッチングは70%とします。
そうすると、
Voアルストとマッチしてブラバする確率、
Viシーズとマッチしてブラバする確率、
ブラバする確率、
ブラバした時にそれがVoアルストが原因である確率
ブラバした時にそれがViシーズが原因である確率はそれぞれ

といった感じになります。Viシーズの方が1.5倍くらい脅威という結果ですね。
え?よく分からなかった?
じゃあよくある分かりやすい説明でも見てください。
参考:条件付き確率の意味といろいろな例題 | 高校数学の美しい物語
独立事象、反復試行
あなたがガシャを100連引いてSSR0枚だったとしても、次の100連でSSRが出やすくなるor出にくくなることが無いといったように、ある試行の結果(事象)が他の試行の結果(事象)に影響しないことを、「それらの試行/事象は独立である」と言います。
これを数式に翻訳するとこうなります。

またこれにより次の式が成り立ちます。
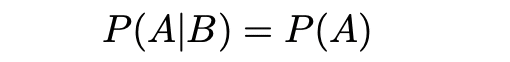
個人的には後者の式の方が直感的に分かりやすいと思います。
これはつまり、「事象Bが起きても事象Aが起こる確率は変わらない関係」ということですね。
これを使うと、反復試行(独立試行を複数回行うこと)の確率を計算できます。
確率pで成功する独立な試行をn回行うとき、r回成功する確率は

となります。これは、確率pをr回、確率(1-p)を(n-r)回引き、かつ「n回のうち何回目で成功するか」でn個の候補からr個選ぶため、nCr種類の場合がある、ということです。個数と一個あたりの確率の積といえば分かりやすいでしょうか。
これを使うと、ソシャゲの確率関連の大部分が計算できます。
例えばノーピック天井の確率とか、トワコレ300連でサポを3枚引き(天井セレチケとピースで完凸)する確率とか。

あとはそのターンに発動するパッシブ(の確率、個数)を指定した時に6個の枠が全部埋まる確率についても計算できます。Le補正を考えないとして、例えば大吉(30%)5個、トリック(30%)4個、カラフル(25%)5個なら(長くなるので計算式は省きますが)17%とか、5個以上発動の確率は35%とか。とにかく確率を足しまくれば計算できます。
excelだとBINOMDIST(r,n,p,0)で計算できます。
この辺りからようやく本題です。
母集団と標本調査
我々はある集合の属性に対して何かを測りたいことがよくあります。グレフェサーのコミュ読む割合がどうとか、tkym氏への忠誠心と天井率とか。
ここで注目するその集団のことを「母集団」と呼びます。
理想的には、母集団の情報を全て集められればそれで終わりですが、数が膨大だったり無限であることがよくあります。
そういうとき、我々はサンプル(=標本)となるデータをある程度の数取ってきて、母集団に対する推測を行います。それを標本調査といいます。(この時サンプルは無作為に抽出しなければいけません。日本人の収入を調べるのにハローワークで聞き込みをすることが賢明とは言えません。)
このとき、よく母集団の要素を小文字(xとか)で、そこから抽出した標本の要素を大文字(Xとか)で書きます。
ちなみに母集団の特徴量、母平均とか母分散とかのことを「母数」と言いますが、「分母の数」、つまり「母集団の全数」や「サンプルサイズ」という意味で誤用されまくっててそっちが市民権を得てるのであんまり使われません。(Twitterで自分の全アカウントでフォロー内検索したら自分含め元の意味で使ってるツイートひとつも無かった)
なのでこの記事では元の英語であるパラメータということにします。
誤用繋がりで言うと、サンプルサイズ(サンプルにおけるデータの個数)のことを「サンプル数」「標本数」(本来はサンプル、標本という集合自体の個数)と言ってしまうのもよくあります。本来の使い方は、「283と765ASを比較するために両事務所のアイドルにある調査を行うと、サンプルサイズは25と13、サンプル数は2」というものです。こっちは正しい使い方もされていますが、フォロー内検索した所やはり正しく使えているツイートは多くありませんでした。
これらは教科書でも間違えてることはありますし、ネットの資料だと結構混同されてることが多いです。私も最近知った
話を戻すと、パラメータについて推測をするのですが、その際主に2つの解析方法があります。それが「推定」と「検定」です。
「推定」は得られたデータからパラメータを推定することで、「このあたり〜」とピンポイントに値を推定する点推定、「ここからここまでの間の数値になる可能性が高いよ〜」とする区間推定があります。
「検定」は「パラメータがもしこんな状況だったら…?」という仮説を正しいものとして仮定して、実際に得られたデータが観測される確率を求め、その仮説が正しそうか調べることです。
区間推定と検定については具体的に後でやります。
平均、分散、標準偏差
この項はあるデータの集まりに関する話です。ただしこれは離散型変数という状態を考えています。詳しくは「離散と連続」の所で。
ここでいう平均はまあフツーの平均なのですが、今後の説明のためにここで説明しておきます。平均は(データの総和)/(データの個数)で計算されますが、そのときサンプルの平均の計算をこのように書きます。(データX1,X2,…,Xnについての平均を考えます)

早い話が「X1+X2+X3+….+Xn」のこと。
この標本平均を表すバー付き文字と和のΣ記号は非常によく使います。
分散は「そのデータの散らばり具合」とよく説明されます。例えば平均が同じデータでも、分散が異なるとそのデータの様子(分布)はかなり違います。
シャニマスで言うと、(銀ピ金ピは無視するとして)SSR確定チケと10連チケ2枚は、平均的にはSSR1枚として同価値ですが、SSR確定は勿論全員SSR1枚な一方、10連チケ2枚は人によってSSR枚数に差が出ますよね。これは前者が分散0、後者は分散があるということです。
母分散はσ^2(^2は2乗の意味)で表し、次のような式になります。

これを見ると、「各要素と平均との差の2乗」の平均という解釈ができます。
勿論こういうときにパラメータ、母分散を知っていることの方が少ないので基本的にサンプルから母分散に近い値を求めることになります。そういった分散の中でも、母平均を知らない場合に母分散を推定する場合は基本的に不偏分散を使います。そしてそれは上の式と少し計算式が一見変わる部分があります。なんかそのままコピーしたような計算式のやつは標本分散(自分が取ったサンプル自体の分散)と言います。実際には母平均を知らない状態からサンプルを集めることがほとんどなので、不偏分散を使うことの方が圧倒的に多いです。
ちなみにですが、これから不偏分散を使ってあれやこれやを計算することになるのですが、これは「母分散=不偏分散」という点推定に基づきます。
計算式はこのようになります。

標本分散と母分散は式の形はほぼ同じに見えますが、不偏分散はnではなく(n-1)で割ってますね。母平均を標本平均で代用する場合はこっちの方が正しい値になるのです。面白いでしょ?
(標本分散と不偏分散の違いについて詳しく知りたい方はヨビノリさんかDS系Vtuberの解説シリーズでも見てください。少し言うと標本分散は最頻値が母分散ですが、不偏分散は期待値が母分散になっています。)
参考:【大学数学】推定・検定入門②(点推定)/全9講【確率統計】 予備校のノリで学ぶ「大学の数学・物理」
参考:【永遠の謎を解明】不偏分散の定義にて n-1 で割っている理由【自由度のお話①】 AIcia Solid Project
勘の良い方は気付かれたかもしれませんが、分散はデータの数値の2乗に比例します。つまり、あるデータの分散に対し、そのデータを10倍して新しく作ったデータの分散は100倍になります。これは不便。
なので、分散に根号(√、ルート)をつけた標準偏差がよく考えられます。イメージ的には「散らばりの平均」といった具合です。平均からどれだけ離れてるか、が散らばりです。
そしてこの分散と標準偏差もめちゃくちゃ大事。後で述べる区間推定にはめちゃくちゃよく関わっています。
豆知識ですが、受験界隈でお馴染みの偏差値はこれを使ってます。結構簡単なので興味があればこの記事とか面白いと思います。
参考:Quizknock 地球上で自分1人だけが問題を解けたら、偏差値は◯◯万だ
excelでは平均はAVERAGE、不偏分散はVAR.S、不偏分散を基にした標準偏差はSTDEV.Sです。(考えているのが母集団である場合は.Sを.Pに変えて下さい)
確率変数、期待値
確率的に値を取る数値のことを「確率変数」と呼ぶことにします。よくXで書きます。この確率は決まっていれば良いだけで、人間が知らなくとも良いです。確率変数はあくまで確率的に決まるので、サンプリングの度に数値が変わるのが普通です。
この項はその確率変数に関する話です。
期待値は平均とよく似た概念ですが、だからこそ敢えて区別しておきます。
確定的した数値(母集団とかサンプルとか)の平均が前項で触れた「平均」、確率的に得られるデータの平均が「期待値」です。もう期待値の説明に平均って言っちゃってますね。
そう、期待値のことを平均とも言います。ただし普通、得られたデータに対する平均を期待値とは言いません。期待値は母集団や確率変数そのものの性質です。
表式としてはこう。

期待値は確率変数に対して計算していることに注意です。
期待値μの試行について、十分大きなサイズのサンプルを取ると、標本平均はほぼμになります。つまりサンプルの平均が期待値に近づく、といった関係です。
同様に、確率変数に対する分散や標準偏差も考えられます。

前項の分散は得られたデータに対する計算でしたが、今回は確率に対する分散です。個数が確率になっていますね。あとサラッと書きましたが、分散が「2乗の平均から平均の2乗を引いた値」というのはそこそこ重要な性質です。導出はこちらで。
参考:分散の意味と2通りの求め方・計算例 | 高校数学の美しい物語
ネイピア数
ネイピア数という数があります。基本eで書く。定義と大体の値がこれ。

初見の方は「え?急に何これ?」となっていることかと思います。誰もが一度は通る道。
ただこれ統計は勿論、この世の数学が使われるほぼ全ての分野で頻出、というより遍在する数なんです。円周率と同じくらい重要。チェンソーマンで言うと闇の悪魔レベル。
ここで少し実験してみましょう。nに1、10、100…1000000まで代入するとこのような式と数値になります。

これについて、nをどんどん大きくしていっても、この値はほとんど変化しなくなります(ちょーっぴりずつ増えていくのみで、ある値を超えない)。こういった、nを際限なく大きくしていくと一つの値に近づいていくことを、「n→∞について収束する」と言います。
定義について細かい話はここで割愛する(しっかり説明しようとすると長くなる)ので、詳しく知りたい方はこのシリーズが分かりやすいんじゃないかと。
参考:【数列】連続複利とネイピア数 ”e” | 大人が学び直す数学
この定義だけでも結構面白い性質があります。
ここで質問。
1%で当たるガシャを100回引いて、1回も当たらない確率はいくらでしょう?
もしかすると、この質問を見て「オイオイ、それはさっきやったじゃないか。100回連続で99%を引く確率、つまり0.99の100乗を計算機で求めるだけじゃないか。」と思った方がいるかもしれません。
ここで私が言いたいのは、これは答えられる人は2秒で答えられるという話です。大体37%です。
これは別に、この問題の答えを覚えていたわけではありません。実は、
「1/nで当たるガシャをn回引いて、1回も当たらない確率」は、nが20以上くらいであれば約37%(=0.37)になります。そしてこの0.37とは1/eのことです。
どういうことかと言うと、上で書いた普通に計算するやり方を式で書くと

この時、eの定義式とnに数値を代入していった時の様子を思い出してみましょう。
これ、eの定義とよく似てますよね?
そしてこのnに大きめの値を代入していっても値はほぼ変わりませんでした。

というわけで、「1/nで当たるガシャをn回引いて、1回も当たらない確率」は、大体1/e≒37%、と分かるのでした。
ちなみに限定ノーピック天井は「1/100で当たるガシャを300回引いて、1回も当たらない確率」、つまり「『1/100で当たるガシャを100回引いて、1回も当たらないこと』が3回連続で起こる確率」なので0.37の3乗、約0.05と確かに求められます。(計算機を使えるならフツーに0.99の300乗を計算しても良いですが、暗算というか「大体このくらいの確率」と見積もる時に知っておくとアンガーマネジメント的に良いです。私は信頼度95%に生きてるので、5%以下の不運を引いたら「世界っておクソ!」となりますが10%くらいなら「世の理ですわ〜」と思います。)
今の話はネイピア数の中でも直接的にソシャゲに関わる部分ですが、数学的には枝葉末節の部分です。
収束する証明とか、微分方程式における重要性とか、三角関数との関係性とかとか面白いことが沢山あるんですけどシャニマスにはあんまり関係ないので泣く泣く割愛します。
数学的な重要性については、まあこのサイトとか見てみるなりすると片鱗がわかるんじゃないかと思います。(重ためなので全部理解する必要は全くないです)
参考:自然対数の底(ネイピア数) e は何に使うのか - Qiita
統計学(大学教養)

知識
・離散と連続
・二項分布
・幾何分布
・正規分布
・中心極限定理
・大数の法則
・χ2乗分布、検定
・t分布、検定
・相関係数
・偏相関係数
・ベイズの定理
・ベイズ統計
項目数は高校数学と同じくらいですが、1つ1つが重ためかも。
これでも結構絞りましたが…
というか高校以前が「数学の森羅万象から学校で教えるごく一部だけを切り取るよー!」となっていただけで、その他が全部高等教育に振り分けられるのでまあそうなるかなと。
離散と連続
これは確率統計というだけでなくこの世界全般を考える際にも大事な概念なのですが、この世の「数値」には2種類あります。それが「離散」と「連続」です。
「離散」は例えば個数とか回数とかサイコロの目とか、整数で表されてるものが多いですが、意味としては「とびとびの数値を取るもの」です。
「連続」は例えば身長とか体重とか確率とか、「どんな2つの異なる数値を取ってきても、必ず間に無限に数字が存在するもの」です。
くじを引いて当たる回数は、1回と2回の間が存在しません。
一方、くじを引いて当たる確率は、作ろうと思えば5%でも5.1%でも、5.00000001%でも作れます。
3年目のテーマ「グラデート」とか、コミュ(アルストとかイルミネあたり)なんかも離散と連続の関係性を意識すると「なるほど」となることがあります。勿論私の感想です。
(デジタルは究極的には離散的なものしか扱えないのですがややこしくなるので、計算上、きめ細かい離散は連続ってことにしてください。)
積分と連続型確率密度関数と分布関数
これは書くか迷ったのですが、今後概念を説明するためには最低限知っておく必要があるので書いておきます。excel等で計算だけ出来れば良いならこの項は読む必要がありません。
ここまでの話は、ほとんど離散的な、確定した確率ばかり考えてきましたが、もっと便利に確率を考えていくために連続的な確率を考えます。
例えばサイコロの目は確率1/6ずつで1~6の目を取る離散型確率変数です。
連続型確率変数もあるわけですが、連続型だと話が少し難しくなります。
というのは、ブラウザバックしないで聞いて欲しいのですが、「連続型確率変数Xがある値xを取る確率」はXやxに関わらず常に0だからです。
いや、気持ちは分かります。常に確率が0ってどういうことだよと。
そうではないのです。ちょっとこの例を見てみましょう。
「今からテキトーに街中で一人を選んで、その人の身長が『ぴったり』170cmである確率」
これ、0なんですよ。
もし仮に「僕の身長は170cmだよ」と言う人がいたとしましょう。じゃあ実際身長を測るわけですが、0.2mmまで測れる測定機を持ってきたら測定結果が身長が169.99cmから170.01cmの間になることはあっても、更に精度の良い2nmまで測れる測定機(現実的にはそのスケールだと熱運動だけで余裕で変わりますが)を持ってきたら170.0000001cmから170.0000003cmの間になるかもしれません。
連続量というのはこれを無限に続けられるので、真の意味で「ぴったり170cm」というのはあり得ません。なので何人取ってこようが確率は0です。
165cm~175cmの集団があったとして、「170cm」の占める割合が1cm精度では1/10、1mm精度では1/100、0.1mm精度では1/1000….と無限に小さくしていけると考えればわかりやすいでしょうか。
じゃあ確率をどう考えるかというと、「今からテキトーに街中で一人を選んで、その人の身長がとある区間、例えば169.9cmから170.1cmである確率」を求めるわけですね。これなら意味もありますし現実的に可能です。
このように、連続型確率変数は、「ここからここまでの値を取る確率」しか求められません。でも各値ごとに「値の取りやすさ」みたいなものが決まってて欲しいですよね。それを確率密度といい、その面積、すなわち積分によって確率になります。確率密度関数f(x)にしたがうXがa以上b以下になる確率は次の通り。

この時のf(x)をXの確率密度関数といいます。あくまでもf(x)は確率を出力する関数ではなく確率密度という、積分されて初めて確率という意味を持つ関数です。
積分ってなあに?という方はこちら。
参考:なぜ定積分で面積が求まるのか | 高校数学の美しい物語
※この中で「微分」が説明に用いられていますが、微分ってなあに?という方はこちら。
参考:微分とは何か? - 中学生でも分かる微分のイメージ - Sci-pursuit
これにより、連続型確率分布の期待値や分散が計算できます。

よく見ると離散型と連続型で、Σと∫の使われ方が似ていますね。実は、Σつまり和を無限に細かくしていったのが積分だったりもします。
参考:定積分と区分求積法
それと、「Xがa以下である確率」を関数として表すと都合が良いので、それをXの(累積)分布関数と呼びます。これは確率を出力する関数ですね。
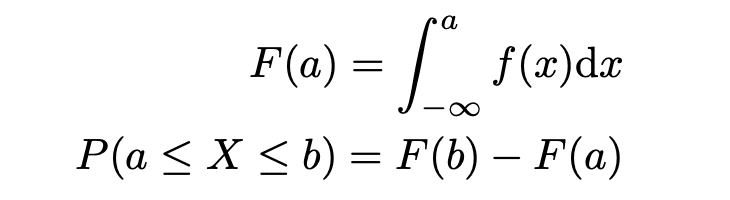
ちなみに次の項からexcelの関数をどんどん紹介していきますが、共通の要素についてはここに書いておきます。
DISTはdistribution、分布のことです。離散型なら確率、連続型なら確率密度を表しています。ただし、excelの最後の引数に「累積」とか「関数形式」という要素があることがありますが、これにTRUEとか1を代入すると累積分布、つまり「Xがa以下である確率」が出力されます。
INVはinverse、逆のことです。
二項分布
ソシャゲの基本。
「当たりハズレの2択の反復試行に対して、当たりが何回あるか」の確率分布です。これは離散的。
確率分布は反復試行の所で書いた話と同じです。

このとき、二項分布に従う確率変数の期待値や分散、標準偏差はこうなります。(当たる確率をp、引く回数をnとする)

これが結構大事で、二項分布において標準偏差はnとpで書けます。
excelだとn回引いてx回当たる確率P(X=x)はBINOMDIST(x,n,p,0)で計算できます。当たるのがx回以下である確率P(X≦x)はBINOMDIST(x,n,p,1)です。
幾何分布
面白い名前してますが、これは「反復試行において、初めて当たりを引くまでに試行する回数」の分布です。つまりガシャ回数ですね(?)。これも離散的。
確率分布は(x-1)回連続で(1-p)を引き、その後1回pを引く確率ですから

こうなります。ちなみにこの時Xがx回以下である確率は

またこの期待値、分散、標準偏差は

になります。
正規分布と中心極限定理
お待ちかね。
正規分布(別名ガウス分布)はもう、各分布の中で最重要と言っても過言ではありません。
これは連続型確率分布なので、確率密度関数で表します。
平均がμ、標準偏差がσの正規分布の確率密度関数がこちら。

式がいかつい。「なにこれ?」って感じだと思います。
けどこれがめちゃくちゃ重要なんです。
この関数は大体こんな形。

そしてこれが重要な代表例がこれ。中心極限定理〜(名前がかっこいい)
中心極限定理とは、
「n個の確率変数{X1,X2,…,Xn}が、互いに独立に平均μ、標準偏差σの確率分布に従うとする。このとき、nが大きくなるにつれ確率変数の平均Xの分布は、平均μ、標準偏差σ/√nの正規分布にいくらでも近づく。」
という定理です。
すごいこと言ってるの分かります?これ、{X1,X2,…,Xn}が従う確率分布について何も条件が無いんですよ。扱う変数がどんな分布だろうと、nがある程度大きければ、その変数の平均はほぼ正規分布なんですよ。
しかも標準偏差が√nに反比例して小さくなるというのもすごい。つまり平均の標準偏差≒区間推定の不確かさを半分にしたければ4倍、1/10にしたければ100倍データを取る必要があると言えるわけですね。
いやあ…すごい(小並感)。
更に言うと、ソシャゲあるあるの二項分布であれば、nが十分大きいとき二項分布は平均np、分散np(1-p)の正規分布とほぼ一致します。ひえ〜
こんな感じで、この世の割と多くは正規分布に従うことが知られています。
ここまで見て、「なんかコイツすごいすごいって言ってるけど何が嬉しいんじゃ?」と思いかもしれません。
めちゃくちゃ嬉しいです。
検定の話になりますが、知らないサンプルが知ってる分布関数に従うと、「こういうサンプルが得られたけどこれって平均はどのくらいからどのくらいまでの確率が高いんですか?」という問いに答えられるようになります。
また分布が二項分布と分かっている場合でも、確率pを知りたい!となったときも嬉しいのですが、それは区間推定の所で詳しくやりたいと思います。
このあたりでこの定理を噛み締めがらコーヒーブレークでもすると良いと思います。
あと正規分布には嬉しい性質があって、
「正規分布に従う確率変数は、定数を足したりかけたりしても正規分布に従う(但し平均や分散は変わる)」というありがた〜い性質があります。具体的には、

これを利用してよく標準化という作業が行われます。
正規分布は平均や分散ごとにバラバラの値を取ってしまうと計算が大変なので、考える確率変数の方を変形して平均や分散を統一しよう!というモチベーションです。
標準化は平均を0、分散を1にすることです。変形としてはこう。

このZが平均0、標準偏差1の正規分布にしたがいます。
標準化された正規分布を標準正規分布と言います。ソノママー
また、標準正規分布の分布関数(標準正規分布の確率変数Zがa以下になる確率)のことをΦ(a)と書くことが多く、例えば「平均μ、標準偏差σの正規分布にしたがう確率変数Xが、aからbの値をとる確率」を求める際にはこのように書きます。

そしてZ=(a-μ)/σとしたとき、excelでは分布関数の値をΦ(Z)=NORMSDIST(Z)と書きます。
これはNORMDIST(a,μ,σ,1)と同じ意味です。
一見同じ関数に見えますが、NORMが正規normal、DISTが分布distributionで、その間に標準standardのSが入るか入らないかですね。
ここまで確率変数にXを使ってきましたが、標準化された確率変数はZで表すことが多いです。
大数の法則
大数の法則は、シュレディンガーの猫並みに誤用されることの多い法則です。恐らく間違いと分かりながらネタで使っている人とマジで間違えている人が半々くらい…?
今回は数式を使わず、お気持ち説明だけで終わらせたいと思います。
(実は大数の法則には弱法則と強法則の2種類がある話とか個人的に面白いと思うのですが割愛)
ズバリ、「独立試行のサンプル数を多くしていった時、標本平均はほとんど確実に母平均に一致する」というのが大数の(強)法則です。
お気持ちとしては「沢山データ取ればほぼ真の値が得られてるってことにしよう!」みたいな感じです。
例えば、あなたが20%のガシャを100回引いて当たりが10回だったとします。これは平均を下回っているわけですが、あと200回引いた時に当たりが増えるわけではありません。大数の法則は「追加で1万回引けば、100回程度のブレなんてないようなもの」くらいの意味です。
区間推定(二項分布と正規分布の例)
上でチラッと書いた、区間推定についてです。「パラメータはこの値の可能性が高い」という点推定ではなく「ここからここまでの可能性が高い」というお気持ちです。
ここでは二項定理の母比率pの区間推定を例にします。
母比率とは真の確率のことで、それについて成功数Xを試行回数nで割ったPで推定します。
中心極限定理により、nがある程度大きければ成功数Xが平均np、分散np(1-p)にしたがうことから、それを標準化した次の量が標準正規分布にしたがうのでした。

これを変形するとこのようになり、

これが標準正規分布にしたがうので、Pが平均p、分散p(1-p)/nの正規分布にしたがうことが言えます。これがミソ。
ここで「パーセント点」について説明します。
α%点とは、ある確率密度関数fにしたがう確率変数Xが上位(下位)α%の結果になった時ときのXの値です。何もつけずに「α%点」と言った時は上位のことがほとんどですが、わかりやすくするために「上側α%点」「下側α%点」と書くことが多いです。
つまりいわゆる「信頼区間95%」(正確には両側95%)は、極端な上振れ2.5%と極端な下振れ2.5%を除いた区間、つまり「求めたいパラメータが95%の確率でこの区間に含まれる」区間のことです。
マイノリティ排除はこの世の摂理。

標準正規分布の上側2.5%点の値が1.96、下側2.5%つまり上側97.5%点の値が-1.96です。これはよく使うので覚えて良いと思います。
次のように式変形を行うと、正規分布に従う確率変数Xは95%の確率でμ-1.96σからμ+1.96σの間であることが言えます。

これを逆にいうと、μは95%の確率でX-1.96σからX+1.96σの間であることが言えます。

これを二項分布に置き換えるとこう。

ここで二項分布はσがpによって表されるので、pを使ってpの区間を求めるというおかしな状況になってしまいます。nが十分大きいということで、大数の法則からpはPで代用します。

このようにして両側信頼区間95%の幅が求まりました。
今回は両側信頼区間95%なので係数は1.96になりましたがこれだけでなく、例えば上側95%とか、両側99%の信頼区間を求めたくなったらexcelのNORMSINV(x)で上側100x%点の値を求められます。上側95%なら-∞からNORMSINV(0.05)、両側99%ならNORMSINV(0.995)からNORMSINV(0.005)になります。
仮説検定(二項検定の例)
※ここで言う検定は頻度論というものに基づきます。詳しくはベイズの所で扱うので、とりあえず今は代表的な1つの手法だと思っていただければ。
仮説検定とは「ある仮説が正しいと仮定したときに、得られたデータと矛盾しないか」というものを検証するためのものです。背理法によく似てます。
検定の手順は
帰無仮説と対立仮説を立てる
有意水準を定める
帰無仮説を正しいと仮定したときのp値(実現確率)を計算する
p値が有意水準より低ければ帰無仮説を棄却、高ければ帰無仮説を採択する
1.帰無仮説が今回の計算の主です。これに沿って「得られたデータ以上に極端な状況が起こる確率」、すなわちp値を計算することになります。基本的に「差がない」という表現であることが多いです。「帰無」というのはnullの訳語らしく、「差がnull(ない)」という仮説が置かれることからこういう名前になったらしいです。
対立仮説は基本的に帰無仮説の「否定」で、「帰無仮説が正しくないならこうなっている」という感じです。これについては完全な補集合になっていなくても良い場合があるのですが、詳しくは二項検定とt検定の所に書きます。
2.有意水準は「どの程度のレアケースまで許容するか」です。小さければ小さいほど起こりにくい状態を考慮に入れることになり、当然範囲はおおきくなります。大体0.01か0.05であることが多いです。この記事では基本0.05にしておきます。これは「5%より珍しい範囲は起こらないものとして考える」ということです。
そして有意水準は実際に計算する前に決めなくてはなりません。何故ならこの検定はp値より大きいか小さいかが全てなので、計算した後で有意水準を変えるといくらでも恣意的に結論が導けてしまうからです。
勿論「5%より珍しい範囲は起こらないものとして考える」という仮定はつまり「平均20回に1回は間違った結論になる」ということでもありますから、そもそも100%正しくなくても良いのが仮説検定です。ただそれを故意にやるのは話が違います。
3.帰無仮説が正しいと仮定して、実際に得られたデータ以上に極端な状態が実現する確率、つまりp値を計算します。この計算に今までやった分布や、後でやるχ2乗分布やt分布を使います。ここは確率累積の計算です。
4.求めたp値と有意水準を比較します。
p値が有意水準より高ければ、「まあそういうこともあるな」と帰無仮説が採択され、低ければ「帰無仮説の場合にこの観測結果になるのはレアケースなので無視!」ということで帰無仮説が棄却され、その否定である対立仮説が採択されます。
このとき、帰無仮説が棄却されれば「正しくない可能性が高い」ということになりますが、採択されても帰無仮説が正しいとされたわけではなく、「今回のサンプルでは間違いとは判断できない」ということを意味します。連続型確率変数と同じような話ですが、「パラメータがぴったりこの値」というのは現実だとほぼありえません。ただ例えば「10%は採択されて9%と11%は棄却される」ならまあほぼ10%ってことになりますし、極限的に正しいとは限りませんが現実的に困らないことがかなりあります。
しかも人為的に作られたプログラムであるソシャゲに関しては、上の例だと10%と言い切ってあまり差し支えないですね。プログラマーが音楽でも聴きながら10%に設定した可能性は高いと言えます。
こういう性格上、帰無仮説には「否定したいもの」が置かれ、対立仮説に「主張したいこと」が置かれることが多いです。帰無仮説は正しくないと言えますが正しいとは言えませんからね。
だからこそ人為的に有意水準を設定したり、p値が設定した有意水準を下回るまでデータを追加すればいくらでも帰無仮説を否定できるようになります。なので仮説検定をするときはサンプルを集めきってから行うようにしましょう。
帰無仮説、内容が否定ですし正しくないという結論が多いしなんだか可哀想な感じがありますね。
無帰無帰にちか〜
一応二項検定の例も紹介しておきます。

これはWINGマスター追加前、というかSTEP追加前に集めていた「歌姫合格なし思い出4以下wing優勝Sランク」の場合の金exのドロップ率です。理由は敗北か、思い出を優先した結果ですので敗北数はまちまちです。
これは科目「ex周回」の指定教科書ですが、これを基に歌姫合格時の思い出4以下の金率を計算すると11.70%になります。サンプルサイズn=16,747、第一回(これは思い出で分けられていないのでこの数字に含めていませんがn=9,391でほぼ同様の数字が得られています)ということで非常に精度の良い値になっているはずなのでこれを真値とします。
明らかに上のデータは金率が低いですね。もしかしたらデータが少ないことが原因かもしれないので、これを検定してみましょう。
ここで帰無仮説を「歌姫合格なしの金率は11.70%」ということにします。対立仮説は「歌姫合格なしの場合金率は11.70%より低い」です。
有意水準は0.01ということにします。
ここで11.70%の試行を306回行った場合の10回のp値、つまり成功するのが10回以下になる確率を求めます。
二項分布の累積はexcelでBINOMDIST(x,n,p,1)を使います。

これは有意水準0.01より低いので、帰無仮説は棄却されます。
ここで一応敗北数についても言及しておくと、上で紹介した記事に敗北数とexの項目がありますが、そこでの敗北数1以上の金率を計算すると11.4%です。(これは思い出5も含んでいますがほぼ影響ありません)
金率に対して敗北数より遥かに大きな影響が出ているのは計算するまでもありません。よって歌姫に合格しないと金ex率は有意に下がることが結論できます。
あとこの話はこの記事で言われていることを前提にしています。勿論皆さん読んでいることかとは思いますが一応。
今回の記事で扱いきれない統計的手法もガンガン使っているので、調べるきっかけになると思います。
χ2乗分布、検定
まずχ2乗分布について。
Z1,Z2,…,Zkが互いに独立に標準正規分布にしたがうとき(勿論このZiは正規分布を標準化した数値でも良い)、その2乗和の分布のことを自由度kのχ2乗分布と呼びます。(χはカイというギリシア文字)


自由度が大きくなるほど左右対称になっていきます。
これの期待値は(標準正規分布の分散の和と式が等しいので)自由度kです。最頻値はk-2です。
数式に目敏い方なら、次に確率密度関数が気になるかもしれませんが、ガンマ関数という説明が面倒な式が出てくるのでここでは出しません。そもそも覚えてなくても困りません。
これの使い方は主に3つで、
①独立性の検定
②適合度の検定
③母分散の区間推定
シャニマス的には主に①と②が重要です。(というか①と②はよく似てる)
順に解説します。
①独立性の検定
ここまで、ソシャゲは二項分布二項分布と書いてきましたが、実際のところ失敗と成功以外の複数の択で考えたい状況はかなりあります。
例えばサイコロの目の出方は6択ですし、シャニマスの約束はVoDaViZZZの4択です。
そのときに、ある複数の分布が異なる確率にしたがうか確かめたいとします。このとき使うのがχ2乗による独立性の検定です。
例えばあるアイドルの2種類のpSSRの約束について、こんな集計結果が得られたとします。

これを見てどうでしょう。
Aの方がVoが多く、Bの方がDaが多く、Viとお休みが大体同じくらいです。かといってめちゃくちゃ明らかな差があるわけでもない。
このデータによって、カード間で約束傾向に差があると言えるでしょうか?
これをχ2乗検定によって確かめます。
検定の手順を具体的に見ていきます。
独立性検定は「差がない」ことを帰無仮説にします。対立仮説は「差がある」ですね。
計算を行うためには「確率の分布はこうなってる」と仮定しなければいけないからです。
「差がない」を帰無仮説におく場合は両方の場合の平均を取ればそれがほぼ真の確率で、これを棄却すれば「差がある」ということになりHappy Endです。
一方「差がある」を帰無仮説におく場合は「どういう差か?」を自分で決めないといけませんし、それを棄却できても「じゃあもっと小さい差だったら?」という話になってしまうのでうまくいきません。
つまり「差がない」ことを実証するのはほぼ不可能なんですよね。「1%以上の差がない」とかならまだ出来ますが。
差がないことを仮定すると、本来の期待値というのはこのようになるはずです。(期待度数表といいます)

期待度数=n*平均確率(AのVoなら0.482*600=289.1)
これが用意できたら、ここでχ2乗分布の出番です。
a×bの表(a,bは2以上とする)において、得られた各項目の数値をOi、仮説による期待値をEiとすれば次の値が自由度(a-1)(b-1)のχ二乗分布にしたがいます。
(片方のみが1の時(b=1)は自由度a-1とします。両方1の時はそもそも検定の対象になりません。)

これをχ二乗分布の分布関数にあてはめれば、それがどの程度のズレなのかp値で出してくれる、というわけです。
まあぶっちゃけこの部分はexcelのCHITESTという関数を使えば一発です。イエー

今回は0.163>0.05なので、帰無仮説は採択され、「カード間で差があるとは言えない」ということになります。
②適合度の検定
①独立性の検定とよく似ています。
これは「予想した分布と実際の分布がどれだけズレてるか?」の検定です。
つまり帰無仮説が「複数のサンプルの分布に差がない」から「予想の分布にしたがう」に変わったわけです。独立性は複数のサンプルの比較でしたが、これは基本的に1つのサンプルについて行うものだと思います。多分。
計算手法的には、独立性検定でサンプルの平均から算出した期待度数表を、自分の予想した分布から算出した期待度数表に変えれば良いだけです。
例として、今回は実測値を見てみましょう。

これは以前書いたnoteで取ったデータです。
これに対して、「まあ均等に1/4ずつかなー」という仮説を立てたとします。これがどのくらい尤もらしいか検定します。有意水準は0.05とします。
期待度数表はこちら。

χ2乗検定をすると

p値が0.792になり、「そこそこあってる」ということになります。嬉しい。終わり。
③母分散の区間推定
ここまで不偏分散は点推定で扱ってきましたが、勿論それにも確率によるブレがあり、不確かさが存在します。
不偏分散と母分散について、次の値が自由度(n-1)のχ2乗分布にしたがいます。

これを用いると、

このように母分散を区間推定できます。(上側パーセント点はCHIINV(x,n-1)で計算できます)
ただシャニマスに限れば母分散を区間推定することがそこまであるわけではなくて、これが重要なのはt分布との関係性だと思います。分散の細かい大小が問題になることがそもそもあんまりないからです。タブン。
あと書く場所が見つからなかったのでここに書きますが、不偏分散と標本平均は独立に分布します。
t分布、検定
区間推定の項で、正規分布を用いて次のように標準化して母平均を区間推定する、ということをやりました。

あれ?ここで何気なく母分散σ使ってますよね?
でも母分散は分からないのが普通です。
じゃあどうするかといえば、不偏分散で代用するのでした。
でも前項で見た通り、不偏分散もχ2乗分布にしたがう確率変数です。
まあnが十分大きければ不偏分散はほぼ母分散に一致するので(目安は母分散の値によって変わりますが大体n=100以上)無視しても良いのですが、それも含めて考えて楽に求められるのであればそっちの方が良いですよね?
そこで使えるのがステューデントのt分布。
標準正規分布にしたがう確率変数Z、自由度kにしたがう確率変数Yに対し、次の量

は自由度kのt分布にしたがうといいます。このときtは正負に対称であることに注意。左右対称なので、絶対値で考えれば十分なことが多いです。というかexcelの関数が絶対値で考えた値しか返しません。
グラフはこんな感じ。
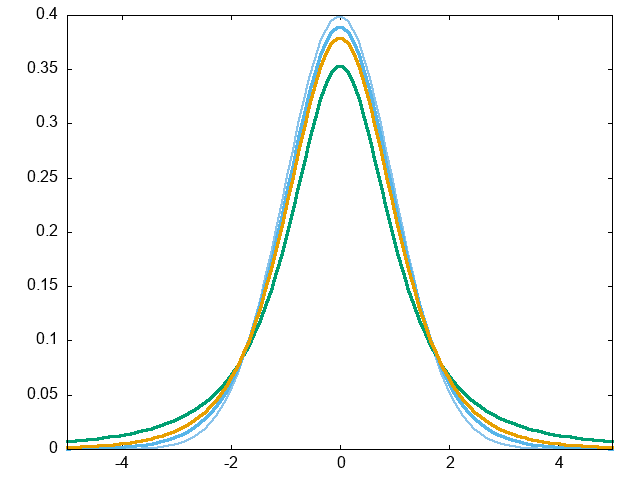
当たり前ですが自由度が増えれば増えるほど標準正規分布に近くなります。
これを正規分布からの標本平均と不偏分散に置き換えるとこう。

これが自由度(n-1)のt分布にしたがいます。
つまり、母分散が分からない時に母平均の区間推定をしようと思ったら正規分布ではなくt分布を使わないといけません。
これを用いるとこんな感じの流れになります。

excelでは、信頼度95%ならTINV(0.05,n-1)で計算します。
TINVは「tの逆関数」で、1個目の引数が有意水準、2個目の引数は自由度です。
またこれを用いたt検定を紹介します。有意水準は0.05とします。
t検定はまあ話の流れから分かる通り、平均に対する仮説検定です。
まず1標本つまりサンプル数1の場合を考えます。
帰無仮説は「母平均が〇〇である」です。ここで対立仮説について注意なのですが、よく平均を考える時は「〇〇より高いor低い」のどちらかのみが重要な場面があります。例えばお菓子の重量が60gと表記されてて、統計的に有意に60gより少なかったら問題ですが、多くて文句を言う人間はあまりいないでしょう。
そういう場合は対立仮説は「母平均が〇〇より低い」ということになります。その場合少し計算が変わります。
例によって例の如くexcelを使う前提で書きます。
t検定ですが使うのはTDISTです。
AVERAGEとSTDEV.Sを使いt値を算出し、その絶対値をとってTDISTに入れてp値を計算します。(当然tの式に代入するμは帰無仮説の値)
まず対立仮説が「母平均は〇〇でない」のときについて。
これは普通にt値が外側の左右0.025の領域に入っていれば帰無仮説棄却、入っていなければ採択です。excel的にはTTEST(|t|,n-1,2)でp値を計算し、0.05より小さければ帰無仮説を棄却し、「母平均は〇〇でない」ということになります。
対立仮説が「母平均は〇〇より小さい」のときについて。
これは片側推定といい、棄却域が片側0.05になります。
excel的には、t値の符号が正ならその時点で帰無仮説採択、負ならexcel的にはTTEST(|t|,n-1,1)でp値を計算し、0.05より高いか低いか判別します。
賢い人なら分かるかもしれませんが、これはt値の符号を判定した上でTTEST(|t|,n-1,2)で計算し0.025と比べたときと同じことです。
対立仮説が「母平均は〇〇より大きい」のときはt値の符号が負ならその時点で帰無仮説採択、正なら計算という感じです。
次に2標本t検定。
これは2つのサンプル間に母平均の差があるか検定します。
帰無仮説は「母平均に差がない」です。
これについて、2つのサンプルというのが同じ集団に対して2回調査を行ったのか(対応がある場合)、バラバラに抽出されたものか(対応がない場合)で計算が違います。
対応がある場合は、2回の各データの差を取った値を使います。これについて1標本のt検定と同じことをします。
対応がない場合、2つのサンプルサイズをそれぞれn1、n2とします。
さらに2パターンに分かれます。まず2つの母分散が等しくない(等しいとは限らない)とき。
これはウェルチのt検定といい、次のt値を使います。

これが自由度n1-n2-2のt分布にしたがいます。
そして母分散が等しいと分かっているとき。
この時2つのサンプルを合体した不偏分散を算出し、次のt値を使います。

これが自由度n1-n2-2のt分布にしたがいます。
相関係数
相関係数は、2つで1組のデータ(Xi,Yi)がある時に、「片方が増えるともう一方がどのように変化する傾向があるか?」を数値化したものです。あくまで傾向なので、必ずしもデータ一つ一つ全てに当てはまる必要はありません。
データの傾向として、
・片方が増えるともう一方も増えることを「正の相関関係がある」
・片方が増えるともう一方は減ることを「負の相関関係がある」
・片方が増えてももう一方は変わらないことを「相関関係がない」
といいます。
例えば課金額と滞在グレードには正の相関があるでしょうし、プレイ歴の長さと潜在true石(未所持恒常も含めた未回収true石)には負の相関があるでしょう。また真乃の総ファン数の下二桁とPデスクのレベルには相関関係がないでしょう、といった感じです。
相関係数にはいくつか種類があるのですが、一番スタンダードな「ピアソンの(積率)相関係数」の計算式がこちら。これを単に相関係数と言うことが多いです。rで表されがち。

これは相関が強いほど絶対値が大きくなるのですが、その数値によってこのようなランク付けがされることが多いです。

ここで注意ですが、ピアソンの相関係数が意味を持つためには2つの変数がどちらも(近似的に)正規分布する必要があったり、大きな外れ値があるとそれの影響を強く受けてしまうといった特徴があります。(ちなみに両方正規分布の場合は、相関関係があるとき直線的な関係になります。)
シャニマスにおいては大体のものが(二項分布の極限として)正規分布に従うので大体これを使って問題ないのですが、そうでない場面もあります。(例えばex検証でそこまでnが大きくない時に虹が短時間に2枚出てしまった時とか)
そこで、このデータにそのまま数値を代入するだけでなく、数値をそのデータ中の順位に置き換えて計算することがあります。
例えば(x,y)=(3,10),(4,80),(5,50),(6,400)のようなデータであれば、
新しく(x,y)=(4,4),(3,2),(2,3),(1,1)と置き換えて計算する、といった感じですね。この時の相関係数を特に「スピアマンの順位相関係数」と呼びます。ρで表されがち。
ちなみに同順位が無いと(連続値がほとんど)こんな簡単に式を出すこともできます。(離散値ばかりのシャニマスだとあんまり使えない)

まあそもそもexcelだとピアソンの相関係数はCORREL関数を使えば良いですし、スピアマンの順位相関係数ならRANK関数で加工してからCORREL関数を使えば良いです。(多分ライブラリ関数に順位相関係数を直接計算するものが無い)
また、相関関係にあるかないかについての検定もここで紹介しておきます。

これが自由度n-2のt分布に従うことが知られているので、例えばexcelでは

このように書いてやると、p値が有意水準(0.05とか0.01とか)を下回れば有意に相関関係があるといえ、上回れば相関関係があるとは言えないということになります。(この例だと0.0049なので有意水準0.01でも有意)
実際に行った分析としては、STEP実装初期において「取るノウハウの数が増えると発現率は減るか?」という問題のために使いました。
偏相関係数
相関係数では「2つのデータの関係性」を算出しましたが、この世には2つパラメータを取ってきたからといって、それが直接因果関係を示すとは限りません。「exスキルとFIP」がそうであったように、AとBの間に有意に相関があっても、AとBが共にCに相関関係があり、Cが変動するとAとBも一緒に変動してただけ、ということもあります。(Aがexスキル、BがFIP、Cが思い出5とか)
その可能性を消すには、Cを一定にしてAとBの値を調べれば良いわけですが、そのためだけに新しくデータを取り直したりCの値で分けたりするのはあまりに大変です。そもそも変数が4つ以上、つまり固定する変数が2種類以上のこともよくありますし、そうなると愚直にやるのはほぼ不可能と言っても良いかもしれません(敗北数や歌姫合格の有無など、調べる変数が4つ以上のことは結構ある)。
そこで偏相関係数という、「他の変数の影響を取り除いたAとBの相関係数」を使います。変数が3つ、つまり固定する変数が一つの場合は計算式は簡単です。ここではzを固定したxyの偏相関係数の計算式を。

2つ以上の変数を固定する場合はちょっと大変です。(主に説明が)
まずサンプルサイズがn個、偏相関で固定する変数がq種類とします。(さっきは1)
手順としては、
① 相関行列Rを求める
② ①の逆行列を求める(R^{-1}と書くことにする)
③ ②の各成分に対し、それに当たる2つの対角成分の積の平方根でその成分を割り-1倍する

はい。正直何言ってるかわからないと思います。ので具体的に説明します。
①まず行列とは何か分かってる人向けに。
今考えるデータにk種類の変数があり、それぞれをa1,a2,…akとします。相関行列とは、i行j列の成分が、aiとajの相関係数である行列のことです。
ここでi行j列の成分とj行i列の成分が等しいことに注意(そのような行列のことを対称行列と言う)。
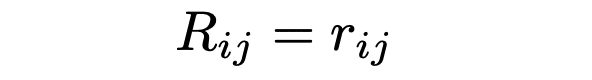
あと先に言っておきますが、偏相関係数の検定は相関係数とほぼ同じです。
繰り返しですがサンプルサイズがn個、偏相関で固定する変数がq種類とします。

これが自由度n-q-2=n-kのt分布に従います。
行列?知らねえぜ!という方はここから行列の説明(重ため)の話が続きますが、偏相関係数を求めるだけなら別に行列を理解する必要はない(excelなどで計算できれば良い)ので、MPとか脳の容量的に厳しい場合は一旦読み飛ばしてもらっても良いと思います。分かってる人は勿論読み飛ばしてもらって良いです。
excelでの実装とか注意点はこの項の最後に書きます。
========ここから行列の説明========
行列とは、行(横の並び)と列(縦の並び)の2次元のマス目があり、それぞれに数字が格納された概念です。その格納された数字のことを成分と呼びます。
excelのシートを思い浮かべてください。縦と横に数字がならんでますよね。あんな感じ。

ここでは行列の中でも、行と列の数が同じ正方行列についてのみ考えることにします。(上の例だと左が4×4行列、右が2×3行列)
ここで上の説明の再掲。
今考えるデータにk種類の変数があり、それぞれをa1,a2,…akとします。相関行列とは、i行j列の成分が、aiとajの相関係数である行列のことです。ここでi行j列の成分とj行i列の成分が等しいことに注意(そのような行列のことを対称行列と言う)。

②行列には行列同士の掛け算があります。定義がこれ。

もうちょっと具体的にやってみましょうか。

これを見ると分かりますが、普通の数の掛け算(3×4=12とか)とは色んなことが異なります。
・掛け算の順番を入れ替えると積も変わる(正方行列に限らなければ、入れ替えるとそもそも掛け算が成立しなくなることがある)
また、
・「1的なもの」(掛け算が成立する限り、かけても元と変わらないもの)があり、それを単位行列という(「1的なもの」を一般に単位元という)

・逆数的なもの(2に対する0.5、10に対する0.1など、積が単位元になる相方)が存在することがあり(相方がいない行列もある)、それを逆行列という(より一般には逆元という)
・逆行列は行や列の数が増えると手計算で計算するのはかなり手間なので、基本的にコンピュータに計算してもらう
ので偏相関係数を考えるだけなら別に行列の積を理解する必要はない、というわけです。
③ 行列には、実は「対角線」が存在します。ただし、これは四角形の対角線とは異なります。察しの良い方は単位行列の所であれ?と思ったかもしれませんが、行列において、「左上から右下にかけての対角線」は特別なのです。それを対角成分と言います。番号で言うと、i行i列といったように行番号と列番号が一致します。
aiとajの偏相関係数を知りたい場合は、②で求めた逆行列のi行j列成分に対し、i行i列成分とj行j列成分の積の平方根で割り、更に-1をかけます。それが上で書いた式。
========ここまで行列の説明========
これをexcelで実装するとこうなります。(例としてこんなデータを考えます。)
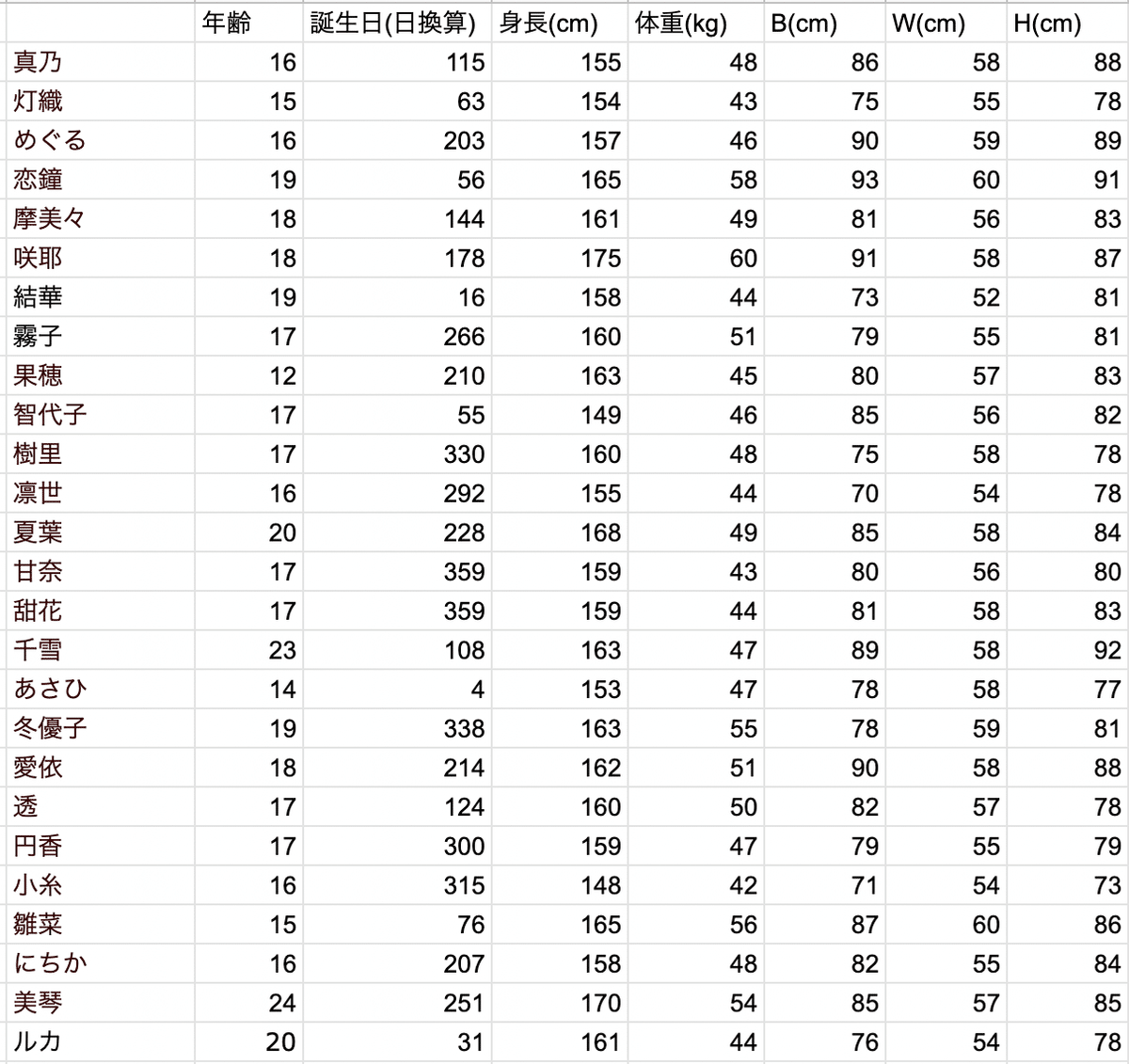
このn=26の7次元(q=5)データを使います。
①まずフツーに相関行列を作ります。

②逆行列を作ります。作りたい所の一番左上にMINVERSE(Mが行列、英語でmatrixの頭文字、INVERSEが逆という意味)を使い、引数に元となる行列を範囲選択してやると自動的に他のセルも使って逆行列を計算してくれます。

③最後に偏相関係数を算出するのですが、このとき式を工夫すると楽です。

「各成分に対し、それに当たる2つの対角成分の積の平方根でその成分を割り-1倍する」(画像だとN28に対し、-N19/√(N18*O19)を計算する)というのは、「各成分」と「-1倍」の部分はフツーにやれば良いのですが、「対角成分」を抜き出すのに一々セルを指定するのは面倒です。
なのでINDEX(指定した範囲から対応する座標のセルの値を抜き出す関数)と
ROW(引数のセル、指定しなければ書いたセルの行番号を取得する関数)と
COLUMN(引数のセル、指定しなければ書いたセルの列番号を取得する関数)を使います。
分かる人は分かると思いますが、一応図解みたいなのを載せておきます。

ROW()は入力したセルであるN28の行番号、28を意味し、ROW($M$26)はM26の行番号、26を意味します。その差が2。つまり、
"INDEX($N$18:$T$24,ROW()-ROW($M$26),ROW()-ROW($M$26))"は
"INDEX($N$18:$T$24,2,2)"
ということで、「N18:T24の中で上から2番目、左から2番目の数値」、すなわちO19の値ということですね。COLUMNについても同じことをやるとN18が指定でき、そして画像のように絶対参照を使うことでオートフィルでぐいーっとコピーできます。つまり入力するのは1回だけ。イェー
かくして、偏相関係数が求まりました。

これを見ると、BとHには強い正の相関、身長と体重にはそこそこの正の相関があることが分かります。
逆に、体重と年齢、身長とスリーサイズや、WとHには偏相関が無いことが分かります。他はともかく身長とW、WとHに偏相関が無いというのは人体構造的にどうなんだろうと思いますね。
ここで相関係数を見てみます。

う〜ん、緑!w
「まあ、身長と体重とスリーサイズが大体帯同してるかな…?」くらいの感想しかないです。
ここで注意なのですが、偏相関係数には多重共線性という問題があります。というのは、偏相関係数は「他の変数の影響を取り除いた2つの関係性」の話なので、変数A、B、CのうちAとBの偏相関を考えるとき、AとCに強い関係性があると、「AとCが関係ある中での、他の要因やノイズによる微妙なズレ(残差という)」とBの関係性を求めることになります。そうするとちょっとの違いで偏相関係数が大きく変わり、数値として信頼できないものになります。イメージとしては、真乃と灯織の絆を考えるのに、めぐるによる影響を除外するのはナンセンスであるといった感じです。
なので偏相関係数を扱う場合は、いたずらに考える変数を増やすと実際的に正しくない(というかあまり意味がない)結果が得られてしまいます。
まあ現実の現象ならさておき、プログラミングという人工物による計算結果であればそこまで気にしすぎる問題ではないと思いますが…
上で得た「身長とWに偏相関がない」もそれが要因である可能性ははあると思うので、興味のある人がいれば変数を減らすなりしてやってみてはいかがでしょうか。
ちなみに、この分析はR(統計用の言語の方)を使うと一瞬です。
excelから.csvファイルをダウンロードして、

数行のコードを書いて実行するだけで、

p値まで全部計算してくれる。つよつよ。
スピアマンの順位偏相関係数を計算する場合は、わざわざRANK関数で加工しなくても「method=”s”」と付け加えるだけで良いです。
無料です。

無料。
ベイズの定理とベイズ統計
ベイズ統計は最近非常に人気な分野です。非常に面白いのですが奥行きありすぎて私の時間的に厳しいので、この記事では意欲のある方向けに軽めの導入と紹介だけしておきます。
ベイズ統計はベイズの定理を基礎として出発した統計手法です。
ベイズの定理の式は全く難しくありません。高校1年生の教科書に書いてあることから容易に導出できます。

ただ難しいのが、「で?」なんですよね。「え、自明じゃん、何が嬉しいの?」となりがちなのがベイズの定理です。
これが強いのは、「時間逆行の条件付き確率を条件順行で表せていること」です。
時間逆行の条件付き確率は、条件付き確率の項で引き合いに出した例以外にも非常に重要な使われ方があります。
それがベイズ統計です。
今までの検定は「もしパラメータがこうならデータが得られる確率はこうだから云々」みたいな感じでしたが、これ結構回りくどいことしてるんですよね。もし「大体こんな感じの予想になっていて、データがこうだから予想はこういう感じに修正、更新される」というように計算できたら楽ですよね。だって前者だとデータの追加があったらまた計算し直す必要がありますが、後者は新しく更新し直せばいいだけです。これが出来るのがベイズ統計。
ベイズ統計では、「パラメータを定数、データを変数として考える(頻度主義という)のではなく、データを定数、パラメータを変数として考える」とよく説明されます。
ベイズの定理を少し変えたのがこちら。
「なんかXというデータが得られたときに、それがあるパラメータθによって起こっていた条件付き確率」を考えます。

分数自体「なんか掛け算してる」くらいのざっくり理解で今は大丈夫です。
これって、「元々P(θ)というθの分布が与えられていたところに、データXが得られたことでそれに新しく重み付けがされて、P(θ)がP(θ|X)という新しいθの分布になった」と考えられますよね。このときP(θ)は真のθの分布になっていなくても構いません。
勿論これは新しくデータYが得られて、P(θ|X)を更に補正していくことが出来ます。こういったことを繰り返して、「データをとっては新しく重み付けをして、真のθに近づいていく」のがベイズ統計です。
もっと具体的に言うと、表の出る確率がぴったり50%ではないコインが2枚あり、片方Aは1000回投げて550回表が出て(表率55%)、もう片方Bは3回投げて2回表が出た(表率67%)とします。
これ直感的にはAの方が表の確率高そうじゃないですか?Bなんて3回投げただけじゃまだなんとも言えませんよね。(残念なことに世の中にはBの方が確率が高いと考える方が一定数いるようですが。)
これをもうちょっと言語化すると、「コインと呼べるくらいには平べったい (≒確率が50%から大きくずれていない)コインに対して、信頼度の高い55%と、信頼性の欠片もない67%では前者の方が説得力がある」といった感じでしょうか。
これは「確率が50%から大きくずれていないコイン」というのがP(θ)、「コインの1000回と3回の試行」が重み付け、それを処理すると得られる「表の確率の予想」がP(θ|X)です。
どうですか?ベイズ統計を使うとこういうことが計算できるんですよ。これは序の口ですけど。
もうちょっと詳しく知りたい方はDS系Vtuberの解説動画でも見てください。
参考:【ベイズ統計その①】条件付き確率と Bayes の定理【時間の流れを意識せよ!】AIcia Solid Project
あとがき
ここまで読み進めていただき本当にありがとうございます。1回読んでどの程度ご理解いただけたかは正直分かりませんが、まず「このnote見ながらexcel使えばなんか数字を出すことができて嬉しい」になっていただき、そこからこのnoteを読みつつ気になることはgoogle先生に聞きつつしていただければ大体のことは分かるようになっているのではないかなと思います。
世間の説明能力つよつよの方には敵うべくもありませんが、少しでも内容をご理解いただき、これからの生活に役立てていただくなり、もっと深く学ぶきっかけにしていただければ重畳です。
それでは良き集計ライフを。
無料のオススメ教材
これは独断と偏見で選ぶ、統計のお勉強するときに見ることが多い無料の教材です。
改めて思うのは、やっぱりデータサイエンスって広く使えるだけあって無料の解説資料めちゃくちゃ豊富ですね。
今回のnoteと難易度レベルが大体同じ内容を扱っている3つと、そこから発展させた内容のもの1つを。
統計学の時間 | 統計WEB
分かりやすいし網羅的だし私いじけちゃうしこのnoteを書くか躊躇っていた最大の理由。
ただ「実際にこんなことするか?」みたいなことまでちょこちょこ書いてあります。しっかり勉強したい人向け。
コグニカル - Cognicull
これは統計というよりは数学、自然科学、工学全般を扱ったものです。
解説サイトとして読むには説明に物足りなさを感じますが、この手の体系知を学ぶ時に重要な「自分は何が分かっていないか、何を学ぶべきか」が分かりやすいです。調べるきっかけにどうぞ。
あと見た目とUIがオサレ。
予備校のノリで学ぶ「大学の数学・物理」(ヨビノリたくみ)
最近の理系大学生のほとんどが知っているとされる。
統計の話についても動画を出してます。分かりやすい。
AIcia Solid Project
上の内容が7割理解できた方向けにオススメしたい。
メチャクチャ分かりやすいしガチで面白いです。
声は男性ですが先入観なしに見て欲しい。
多分1本見終わる頃にはめちゃくちゃ可愛く感じてます。
この記事が気に入ったらサポートをしてみませんか?
