第６回 Torus-P(n)-Leaper

前回の続きです。

---

無限盤上の$${L(a,b)}$$は$${a,b}$$の組合せで無限の種類がありますが、$${\textrm{Torus-}(a,b)\textrm{-Leaper}}$$はどれくらい種類があるでしょうか。

$${(a,b)\textrm{-Leaper}}$$について

$$
\begin{align*}
&L(a,b) \\
=&L(-a,b) \\
=&L(a,-b) \\
=&L(-a,-b) \\
=&L(b,a) \\
=&\cdots
\end{align*}
$$

が成り立つ上、トーラス盤で考えれば$${a,b}$$は$${\mathbb{Z}/9\mathbb{Z}=\{0,1,2,3,4,5,6,7,8\}}$$の元なので$${a,b}$$の組合せは限られています。そのため、$${(a,b)\textrm{-Leaper}}$$はそこまで多くの種類はありません。

実際に確認すると下記が分かります。

命題６.１
$${9\times9}$$の$${\textrm{Torus-}(a,b)\textrm{-Leaper}}$$は下記の15種類である：

$$
\begin{matrix}
L(0,0) & L(0,1) & L(0,2) & L(0,3) & L(0,4) \\
 & L(1,1) & L(1,2) & L(1,3) & L(1,4) \\
 & & L(2,2) & L(2,3) & L(2,4) \\
 & & & L(3,3) & L(3,4) \\
 & & & & L(4,4) \\
\end{matrix}
$$

（証明）
$${L(a,b)}$$の性質から、$${a\leq b}$$かつ$${a,b\in \{0,1,2,3,4\}}$$なる$${(a,b)\in\mathbb{Z}\times\mathbb{Z}}$$が$${L(a,b)\subset\mathbb{Z}/9\mathbb{Z}\times\mathbb{Z}/9\mathbb{Z}}$$に1対1に対応することが分かる。
（証明終わり）

次に$${\textrm{Torus-}P(n)\textrm{-Leaper}}$$を考えます。

まずは、以前に定義した無限盤上の$${P(n)\textrm{-Leaper}}$$の定義を復習しましょう。

ーーーーーーーー

定義（Pn-Leaper）
$${n\in\mathbb{N}}$$に対し、無限盤上の$${P(n)\textrm{-Leaper}}$$を下記で定める。

$$
P(n)=\sum_{a,b\in\mathbb{N},n=ab} L(a,b)
$$

ただし、$${L(a,b)}$$は無限盤上の$${(a,b)\textrm{-Leaper}}$$である。
なお、$${P(n)\subset\mathbb{Z}\times\mathbb{Z}}$$である。

ーーーーーーーー

なお、上記は以前の定義から記載を少し変更していますが、内容は変わりません。

$${\textrm{Torus-}P(n)\textrm{-Leaper}}$$とは、上の定義の$${L(a,b)}$$を$${\textrm{Torus-}(a,b)\textrm{-Leaper}}$$とした駒のことと定められます。

定義６.２
$${n\in\mathbb{N}}$$に対し、$${9\times9}$$の$${\textrm{Torus-}P(n)\textrm{-Leaper}}$$を下記で定める。

$$
\textrm{Torus-}P(n)=\sum_{a,b\in\mathbb{N},n=ab} L(a,b)
$$

ただし、$${L(a,b)}$$は$${9\times9}$$の$${\textrm{Torus-}(a,b)\textrm{-Leaper}}$$である。
なお、$${P(n)\subset\mathbb{Z}/9\mathbb{Z}\times\mathbb{Z}/9\mathbb{Z}}$$である。

では、$${\textrm{Torus-}P(n)\textrm{-Leaper}}$$の具体例をいくつか確認してみましょう。

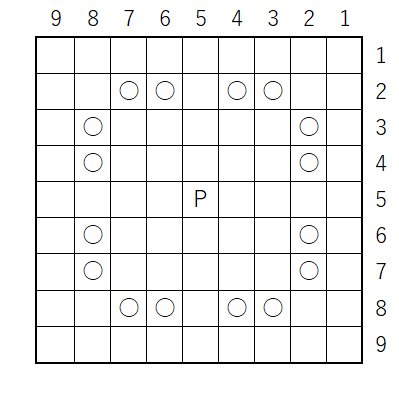
例６.３

$$
\begin{align*}
&\textrm{Torus-}P(6) \\
=&\sum_{a,b\in\mathbb{N},ab=6} L(a,b) \\
=&L(1,6)+L(2,3)+L(3,2)+L(6,1) \\
=&L(1,6)+L(2,3) \\
=&L(1,3)+L(2,3) \\
& \\
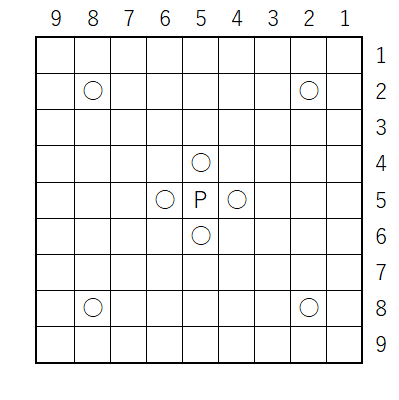
&\textrm{Torus-}P(9) \\
=&\sum_{a,b\in\mathbb{N},ab=9} L(a,b) \\
=&L(1,9)+L(3,3)+L(9,1) \\
=&L(1,9)+L(3,3) \\
=&L(1,0)+L(3,3)
\end{align*}
$$

P=Torus-P(6)

P=Torus-P(9)

注意６.４
$${\textrm{Torus-}P(n)}$$の$${n}$$に対して$${9=0}$$のルールを適用することはできない。例えば

$$
\begin{align*}
&\textrm{Torus-}P(12) \\
=&L(1,12)+L(2,6)+L(3,4) \\
=&L(1,3)+L(2,3)+L(3,4)
\end{align*}
$$

だが、$${\textrm{Torus-}P(3)=L(1,3)}$$である。つまり、$${\mathbb{Z}/9\mathbb{Z}}$$上で$${12=3}$$だが

$$
\textrm{Torus-}P(12)\neq\textrm{Torus-}P(3)
$$

が成り立っている。

一般には注意６.４の通りなのですが、異なる整数$${n,m}$$に対し$${\textrm{Torus-}P(n)=\textrm{Torus-}P(m)}$$となる場合もあります。

例６.５

$$
\begin{align*}
&\textrm{Torus-}P(2) \\
=&L(1,2) \\
=&L(1,11) \\
=&\textrm{Torus-}P(11)
\end{align*}
$$

である。また、

$$
\begin{align*}
&\textrm{Torus-}P(8) \\
=&L(1,8)+L(2,4) \\
=&L(1,1)+L(2,4) \\
& \\
&\textrm{Torus-}P(10) \\
=&L(1,10)+L(2,5) \\
=&L(1,1)+L(2,4) \\
\end{align*}
$$

なので、$${\textrm{Torus-}P(8)=\textrm{Torus-}P(10)}$$である。

整数$${n,m}$$がどのような関係のときに

$$
\textrm{Torus-}P(n)=\textrm{Torus-}P(m)
$$

が成り立つのか整理するのは、今後の課題としておきます。

---

$${\textrm{Torus-}P(n)}$$を使用したフェアリー詰将棋を作りました。2022年に関連しているので、年賀詰ということにしています。

次回はこちら。