
基礎編14 「2つ取り出すの分母②」取り出して,戻さずもう1回
7から10までの整数が1つずつ書かれた4枚のカードがある。これらのカードをよくきってからAとBの2人が続けて1枚ずつひく。Aがひいたカードに書いてある数を$${a}$$,Bがひいたカードに書いてある数を$${b}$$とするとき,$${a-b}$$の値が2以上になる確率を求めなさい。
ただし,ひいたカードは戻さないこととし,どのカードをひくことも同様に確からしいものとする。
(山梨県2017)
問題を解く前に・・・
「ひいたカードを戻さない」ことに注意しましょう。今までになかった考え方が出てきますよ。
分母は・・・
Aさんにとって起こる偶然は「7をひく」「8をひく」「9をひく」「10をひく」の4通り。

その後にカードをひくBさんにとっても,起こる偶然は「7をひく」「8をひく」「9をひく」「10をひく」の4通り。

表はこんな感じになります。

ここまでは基礎編13と違います。が! ここからが本日のメインイベント。2人の偶然はお互いに影響をするときは,ここからもうひとつ作業が必要になります。
Aさんがひいたカードは戻さないために、2人の偶然はお互いに影響をするのです。もう少し詳しく説明しましょう。
もしAさんが7をひいてしまったら,Bさんは7はひけなくなります。AさんもBさんも両方7をひく、ということは起こり得ないのです。これが「2人の偶然はお互いに影響をする」ということです。
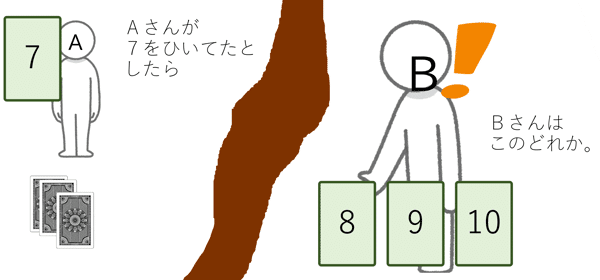
Aさんが7をひいたとき、そのほかの「Bさんが8をひく」「Bさんが9をひく」「Bさんが10をひく」ということは、同様に確からしく起こります。なので、表の中で「Aさんが7をひいて、Bさんも7をひく」になってしまう表のマスに×をつけましょう。

Aさんが8をひいてしまったら,Bさんは8はひけなくなります。同じように表に×をつけましょう。

・・・もうお気づきでしょうか? Aさんが9をひいてしまったら,Bさんは9はひけなくなります。10のところも同じですね。というわけで,同じように×をつけておきましょう。

表のななめに×がピーっと入ります。このように,カードを戻さないと,表をいじる,ということが起こります。
表の中で×のついていないマスを数えると,12通り。この12通りが、AさんとBさんがこのようにカードをひいたときに同様に確からしく起こることがら、ということになります。
分子は・・・
$${a-b}$$の値を表の各マスに書き入れましょう。

$${a-b}$$の値が2以上の値をとるのは,表に○をした3通りです。2以上といったときに2も含まれるのは,大丈夫ですね?

確率を求めると、$${\dfrac{3}{12}=\bm{\dfrac{1}{4}}}$$
答え
$${\bm{\dfrac{1}{4}}}$$
問題を解いた後に・・・
このように,取り出したあとに戻さないときには,表をいじることになります。
2人の偶然の間に影響があるときは、表をいじる
さらにもうひとつ,次の基礎編15で表をいじるもうひとつのパターンをやりましょう。そのために意識しておいてほしいのは「1枚目→2枚目」の順序があることです。「同じカードは取り出すことができないけど、順序がある」ときの形をP型と呼んでおくことにします。
問題を解いた後、さらに・・・
順列ということばを知っていたり、Pとかの記号や公式を知っている人からすると、なんだ分母は$${{}_4\mathrm{P}_2}$$で求めればいいじゃないか、と思うかも知れません。
複数の偶然で構成されている場合、まず1つ1つの偶然に解きほぐして(1人1つに分担をして)、1つの偶然が起こった後「可能性が1つ減る」という肌感覚がないところで、単純に「この問題のパターンは順列だから公式に当てはめて」とやっていると、それ以上の
だからこそ、中学の確率問題といういわば「おもちゃ箱」で、まずは肌感覚というか、直感力というか、そういうものを養って慣れておいてから、もう少し抽象的なところに行った方がいいと思っています。その先単純に公式を当てはめればよいわけではない問題や、はっきり順列を適用すればいいとは改訂ないような問題に直面したとき、「これこれ」と当てはめる考え方がすっきりとできるのでは、と思います。
このnoteで目指しているのは、まさしくはじめてこの「おもちゃ箱」で遊ぼうとするときに、「しょせんおもちゃだよ、大人はこういう道具を使うんだぜ」としないで、まずはおもちゃで安全に遊んで感覚をつかんで、次のステップに行く、というそういうことだと思っています。
いろいろなおもちゃで遊ぶうちに、無目的に見えるかも知れないけど、いくつかの本質的なものの見方や考え方が身に付く,ということなのだと思います。
-----------------------
<前の問題 次の問題>
問題一覧
類題 山形県2022 熊本県2021、沖縄県2020,北海道2019、愛知県B2019、島根県2019、栃木県2018、滋賀県2018、北海道2017
、岩手県2017ほか
-------------------
※ 2023.2.19 例題を差し替え。もとの問題や解説は基礎編30.5にカテゴリー変更。
この記事が気に入ったらサポートをしてみませんか?
