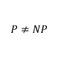
大学の(基礎的な)数学科目を受けた感想 その5 離散数学
こんにちは、これが83本目の記事となったすうじょうです。さて、今回は大学生になって受けた数学科目について教科ごとに、当時を思い出しながら感想を言うシリーズの5回目をやっていきたいと思います。今回は基礎と言っていいか微妙な離散数学です。
前回までの感想は以下の記事です。
離散数学
次に、大学数学の科目の中で工学系(情報系)と理学系くらいしか教わらないのではないかという離散数学について話していきます。調べていないので分かりませんが、ほとんどの理系の方は習わないのではないかと勝手に思っています。内容としては、大学や学部によってぶれると思いますが、私の場合は以下の内容でした。
・集合論と組み合わせ論
高校数学の集合の復習とその定義、集合の集合
集合演算、べき集合
命題論理と論理式
述語論理
直積集合と2項関係
半順序関係と同値関係
集合による関数の定義
有限集合と無限集合(集合による自然数の定義)
実数の非可算無限性の証明・カントールの対角線論法
数学的帰納法
差分方程式の解法
・グラフ理論
グラフと関連用語、概念
オイラーグラフ、ハミルトングラフ
木とその性質
幅優先探索と深さ優先探索
最小全域木とクラスカルのアルゴリズム
最短経路(最短の道)とダイクストラのアルゴリズム
ネットワークとフロー
最大フローとフォード・ファルカーソンのアルゴリズム
連結度、メンガーの定理
マッチング、ホールの定理
平面グラフ、オイラーの公式、クラトフスキーの定理
グラフ彩色と4色定理(5色定理)
場合によっては、一部習う内容が多い、少ないなど異なることがあると思います。しかし、私が受けた授業の概要はこのような感じだったと思います。私自身は、カリキュラムの都合だと思いますが、組み合わせ論についてほんの一部しか取り扱いませんでした。
ここで、分からない方がいると思うので、一部軽く解説します。
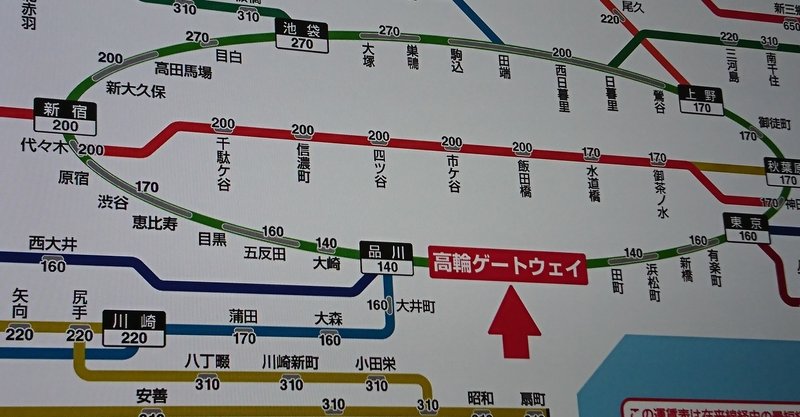
離散数学というのは、連続でないもの(整数、離散グラフなど)を対象としている数学分野の集合科目で、コンピュータの登場とともに発展したため、まだまだ研究や発展の余地のある分野です。また、グラフ理論における離散グラフというのは、x-y平面に描いた直線や曲線のことではなく、主に電気回路や地図などを指し、分かりやすい例はタイトル画像の路線図をイメージしていただければ分かりやすいのではないかと思います。
感想としては、大学で数学系の講義を受けるのに少し慣れていた段階だったのに加えて、理論色の強い科目だったので、苦労もありましたが、無事単位を獲得することができました。集合論のところは理解する必要があり、差分方程式の解法暗記、グラフ理論は、定義やアルゴリズムについてそれぞれ暗記と手作業での再現が必須だったので、苦労しました。全体的に、一部の証明の理解は当時諦めていました。基礎科目という印象がないのもそれら所以かもしれません。しかし、他の情報科目の基礎になるという意味では、基礎科目であったと思います。講義の内容としては、理論重視で押さえていき、目標としてはきちんとした理解のもと問題に取り組むことができ、アルゴリズムの仕組みを説明できることだった気がします。今考えてみると、差分方程式は微分方程式とかなり解法が似ていたと思います。細かい理論や証明については、参考資料をもらいましたが理解は完全にはしていなかったと思います。高校の時はなかったような分野なので、大学での情報系を専攻することの実感を湧かされた科目でした。
以上が私の感想です。一応、数学の基礎科目の感想を言うシリーズはこれで一区切りですが、今後他の情報科目の感想を言うシリーズを始めるかもしれません。では。
この記事が気に入ったらサポートをしてみませんか?