- 運営しているクリエイター
#ロドリゲスの式
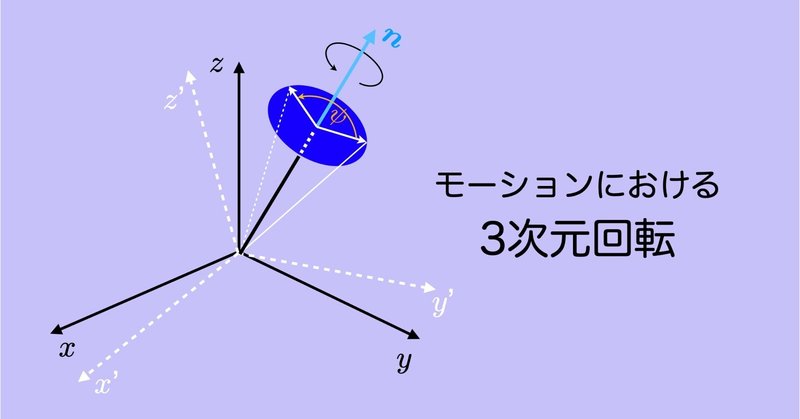
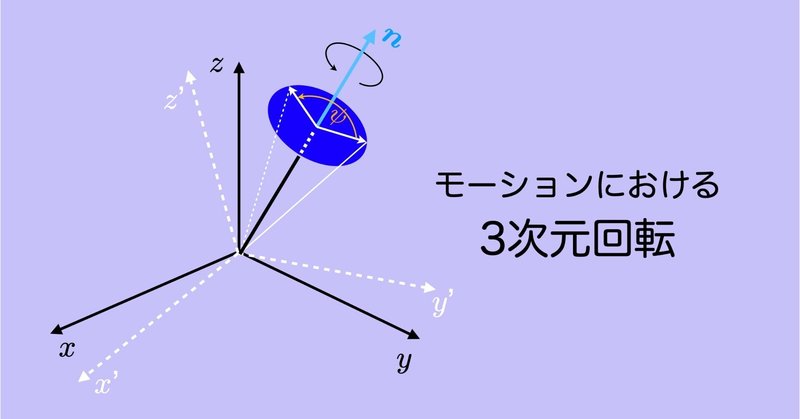
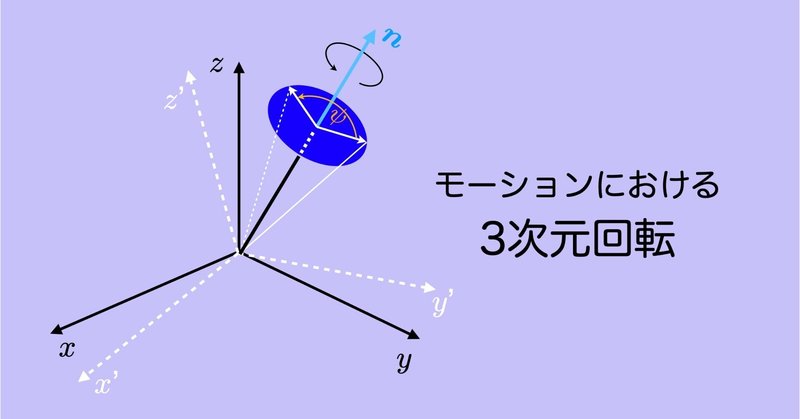
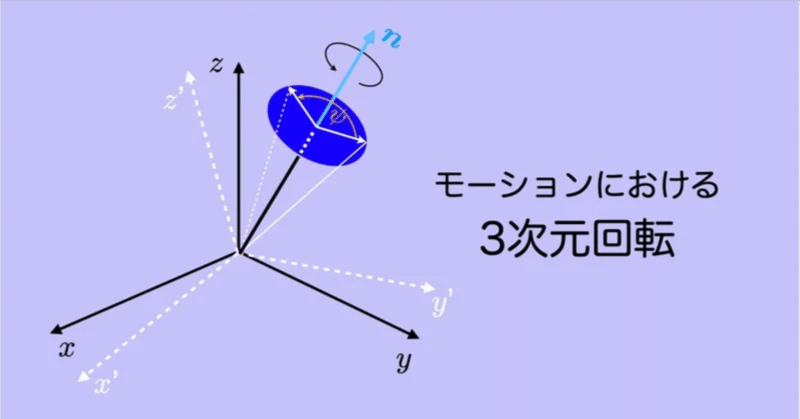
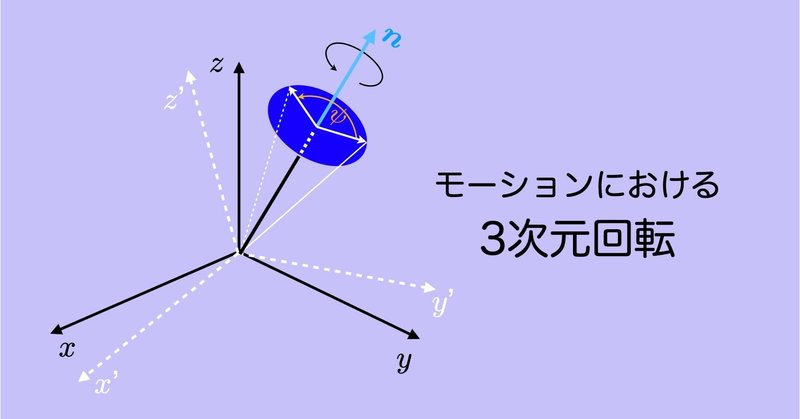
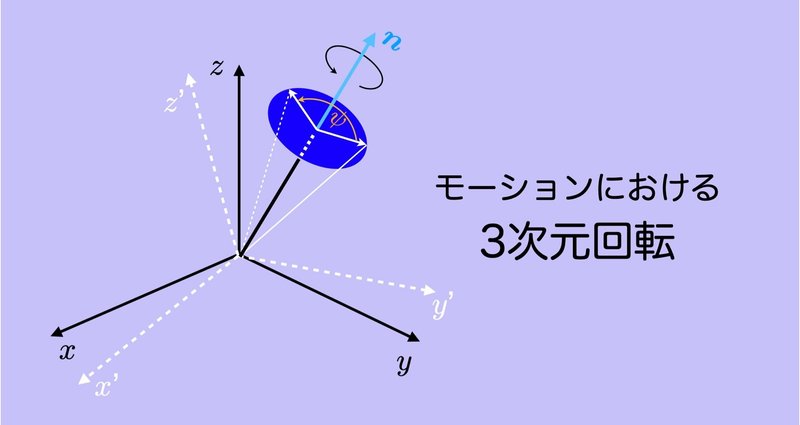
モーションにおける3次元回転 #8 〜単位クォータニオンによる回転合成〜
単位クォータニオンの演算ここでは,回転合成と前章まで議論したロドリゲスの式の,単位クォータニオン(オイラーパラメータ)による表現を示す.
回転合成の節では,行列表現によってクォータニオン同士の線形計算ができることを示すが,この行列表現を用いることでMatlab, Python(Numpy)などの行列計算を利用でき,プログラミングの記述も行いやすくなり.計測制御の観点では,行列表現によってKalm
モーションにおける3次元回転 #7 〜単位クォータニオンによる回転表現〜
単位クォータニオンクォータニオンから単位クォータニオンへ
ここであらためて定義するが,クォータニオンは
$$
\bm{q}=q_0+q_1 i+ q_2 j + q_3 k=\begin{bmatrix}
q_0\\q_1\\q_2\\q_3
\end{bmatrix}
=\begin{bmatrix}
q_0\\ \bm{v}
\end{bmatrix}
$$
のように,実数で記述されたス
モーションにおける3次元回転 #6 〜クォータニオンの導入〜
単位クォータニオンとオイラーパラメータクォータニオン(quaternion)は四元数(しげんすう)とも呼ばれ,アイルランドの数学者ハミルトンが1843年に,現在ウィリアム・ローアン・ハミルトン橋と呼ばれている橋を歩いているときに,ひらめき,そのアイデア(下記の式)を橋にナイフで刻んだと伝えられている.
なお,回転を含めた2次元平面の幾何学を記述する複素数が,4次元へ拡張されたのものがクォータニオ
モーションにおける3次元回転 #5 〜ロドリゲスの式の幾何学的意味〜
前章「モーションにおける3次元回転 #4 」で,3次元回転を表すロドリゲスの式について述べたが,これは2次元平面の回転を複素数で表すオイラーの公式から単位クォータニオンへの橋渡しと位置づけていたが,もう少し補足する.
復習
図1のように,複素平面で虚数$${i}$$をかけることは,複素平面上の原点まわりの回転を意味する.
例えば,図1の実数軸上の一番右の点である$${1}$$に「虚数 $${i
モーションにおける3次元回転 #4 〜オイラーの公式からロドリゲスの式へ〜
前章「モーションにおける3次元回転 #3 」では,オイラーの公式を用いて2次元平面内の回転について説明した.
2次元と比べて3次元の回転運動の表現方法はかなり複雑である.この章では,3次元の回転行列のもう一つの表現方法である,ロドリゲスの式について説明する.クォータニオンはロドリゲスの式と密接に関係することから,ここでの目的は,これを学ぶことによって,次章(モーションにおける3次元回転 #5 )で述