
【解説】モノの大きさや小ささを意識した発想/東京大学 1997年 後期試験数学
こんにちは。少しご無沙汰しております。
今日は久々に東京大学の数学の入試問題を1つ、紹介しようと思います。1997年東大後期試験の数学の問題の1つです。
解法をこんな感じで考えていけばいいんじゃないかというのを後述していますので、まずは何も見ずに解き方を考えてみてください。方針だけであれば、紙やペンがなくても、最後まで頭の中で考えることは可能です。ぜひ挑戦してみてください。
問題
下図のように、1 辺の長さが1 の正3 角形で、平面を分割する。

これらの1辺の長さが1の正3角形1つ1つを、単位正3角形と呼ぶこととする。はじめに1個以上有限個の単位正3角形が塗りつぶされているとし、以下の操作を繰り返すことにより、次々に単位正3角形を塗りつぶしていく。
「1回の操作ごとに、既に塗りつぶされている単位正3角形と少なくとも1つの辺を共有する単位正3角形をすべて塗りつぶす」
次の問に答えよ。
(1)はじめに塗りつぶされている単位正3角形が1つだけのとき、n回目の操作が終わったときに塗りつぶされている単位正3角形の個数anを求めよ。
(2)はじめに2個以上有限個の単位正3角形が塗りつぶされているとき、n回目の操作が終わったときに塗りつぶされている単位正3角形の個数をbnとおくと、極限
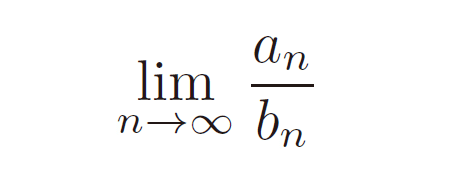
は、はじめの塗りつぶされ方がどのようであっても存在するか、極限が存在する場合についてはその極限を求めよ。存在しない場合があるならば、その例をあげよ。
では解説にいきたいと思います。よろしいでしょうか。
解説
まず(1)ですが、自然数n が絡む問題で、しかも状況がいまいち掴みにくい場合には,とりあえず具体的に「n = 1, 2, 3, 4, 5, · · · 」を代入してみて、今回であれば図を描いてみるのがセオリーですね。
本問題の繰り返し操作は、何となくフラクタル図形のコッホ曲線(雪の結晶)の描き方が想起させられますが、あちらは線分
を3等分してから中央の線分に対してのみ正三角形を追加していくものであり、今回の操作とは異なるので考えないことにしましょう。
(フラクタル図形の雪の結晶と聞いてピンと来ない人は是非コッホ曲線で画像検索してみてください!)
初めに塗る三角形の向きは△の向きのものであると考えても一般性は失わないため、この向きのまま解き方を考えていきます。そして、具体的なnの値に対していくつか図を描いていくと、徐々にどのような図形が拡がっていくかが見えてきます。
ここで中途半端に「n = 1, 2, 3」 あたりで図を描くのを止めてしまうと、n が大きくなっても全体像が何となく三角形になってしまうように錯覚してしまうかもしれません。どのような図形が出来上がっていくのか明確にイメージできない場合は、思い切ってn の値を多めに代入して、問題の裏に潜むルールをしっかり探っておきましょう。そして、「n = 5」 あたりまで代入して得られる図形が下図になります。1 回の操作ごとに色分けして、どの三角形が何回目の操作で追加されたのか視認しやすくしています(入試では色ペンの類は使用できませんけれども・・・)。
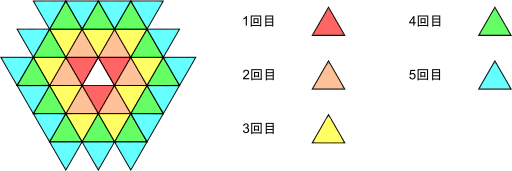
もし、余裕があれば、「n=6、7」あたりまで代入していくと、全体像が正6角形に近づいていくのが予想できると思います。(コッホ曲線も三角形からスタートした場合は全体像が正6角形のようなものに近づいていくので、本問題と似ていると言えば似ていますね。)また、図を描くことによって、おそらくanの階差数列が初
項3,公差3の等差数列になっていることも予想できます。
実際の解き方ですが,全体像が正6 角形に近づいていくのがイメージできれば、正3 角形が追加されていくルールも把握し易くなります。ただし、nが偶数か奇数かで、どの辺が線分になり、どの辺がギザギザ(山谷繰り返し)になるかが交互に入れ替わるため、場合分けが必要になります。とはいえ、線分のところは単位正3角形の個数と同じだけの三角形が追加され、ギザギザのところは山の数より1 だけ小さい単位正3 角形が追加されるだけですので、実際には完璧な議論ではなくともそれなりの解答は書きやすいのではないでしょうか。
最終的にはnの値の偶奇に関わらず
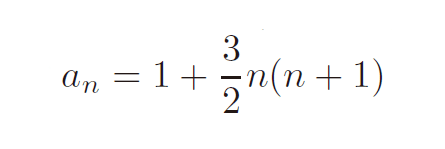
であることが導かれます。
東京大学の入試の特徴
では次に(2) ですね。具体的な解説に入る前に、少し東京大学の入試問題の特徴についてお話ししようと思います。
東京大学の数学や理科の入試では、非常に大きい値や小さい値について,或いはめんどくさい計算が昔からとても多いです。様々な誤差の計算で四苦八苦する工学部を出た身として振り返ってみると、値の大きさに対する感覚をこの時点でもっておくのは非常に重要であることのように感じられます。
受験生には、入試勉強を通じてそういう感性を研いでほしいと思っているのかもしれませんね。
実際今回の問題の(2) では、そういう大きさに対する感覚がもてているかどうかで解法の思い付き易さが変わってきます。
問題文を読んでみて、いまいち何を言っているのか分かりにくいと思うので、ちょっと実験してみましょう。下図のように、とりあえず初期状態として三角形を3 つ塗ってみることにします。
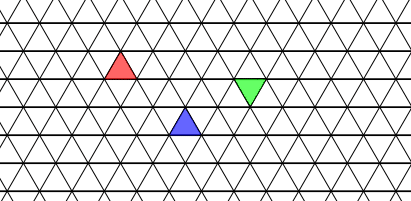
この初期状態に対して、n=5の段階まで状態を進めてみると、下図のようになります。
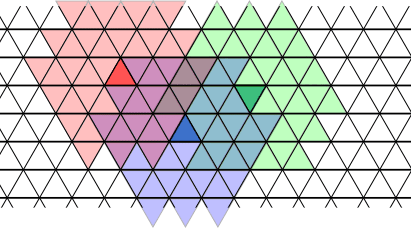
・・・正直この段階では何が何だか分かりませんね。
しかし諦めてはいけません。元の問題文ではn=5どころかn→∞の状態を考える必要があるのです。
ここで、1つ1つの三角形に対しては、正六角形に近い形の図形が形成されていくさまを(1)で確認したのを思い出してください。n → ∞ の状態では、遥か上方から平面を見下ろすと、かなり綺麗な正六角形がおそらく出来上がっていることでしょう。
さらにそのように上方から見下ろしたときに、初期状態で配置された3 つの三角形はまるで1 か所に集まっているかのように見えるのが分かりますね。
ということは、大きな視点で見れば、初めにどれだけ三角形が塗られていたとしても、n → ∞ の大きな視点で見れば、もはやそれはたった1 つの三角形からスタートしたと考えても大して変わらないことになります。
つまり、最終的にできる図形は、初期状態で塗られる三角形がたとえいくつであっても、そしてさらにどれだけ離れていたとしても、結局は大きな大きな正六角形もどきになると言えます。
実際の証明でははさみうちの原理を用いて厳密に証明しますが、発想の源は上記のような大きな視点になります。
今回の問題は後期試験をテーマにしたため,難易度が通常の入試よりも結構難しいと感じる方が多いと思いますが、受かることだけを考えるならばこの難易度の問題はよほど数学に頼りきりの受験生でなければ解ける必要はありません。
とはいえ、モノの大きさや小ささを意識した発想というのは特に東京大学の数学の入試問題では重要になりますので、頭の中に留めておいてください。
では、また。
■自己紹介
■国公立大学の数学問題を、思考法を含めて解説しています。
■受験勉強に役立つ、数学コラムを投稿しています。
この記事が気に入ったらサポートをしてみませんか?
